基于深度学习的高中数学课堂教学模式初探*——以“椭圆及其标准方程”课时为例

福建省厦门市厦门实验中学(361100) 杜晓欢

《普通高中数学课程标准》(2017 年版2020 年修订)指出: 在教学实践中,要不断探索和创新教学方式,不仅重视如何教,更要重视如何学,引导学生会学数学,养成良好的学习习惯;要努力激发学生数学学习的兴趣,促使更多的学生热爱数学. 因此本文提出了“启智”课堂教学模式,希望能够启迪学生的数学智慧,并试图为高中数学教师的课堂教学提供可以参考的实操方法和案例,帮助教师在新教材和新课标的背景下尽快跟上节奏,更好地组织课堂教学,应对新高考.

1 模式缘起

“启智”课堂的教学模式充分借鉴了深度学习的相关理论,而深度学习的提出,既是对教学规律的尊重,也是对时代挑战的主动回应. 深度学习是落实核心素养的重要途径,是信息时代对知识教学的反思和改进. 深度学习的研究与实践,确立了学生个体经验与人类历史文化的相关性,落实了学生在教学活动中的主体地位,使学生能够在教学活动中模拟性地“参与”人类社会历史实践,形成有助于未来发展的核心素养,而教师的作用与价值也在深度学习中得以充分实现. 实施“启智”课堂的教学模式后,教师能更好地引导学生进行深度学习,达到课程标准的要求.

2 模式架构

“启智”课堂的教学模式架构是一颗“智慧果”(如图1),其中教学环境是“智慧果叶”,为整个教学的展开提供客观条件的支持;问题串是“智慧果核”,是课堂的核心组织形式,是一个循环设计“问题——追问”的过程;“明暗两线”是“智慧果肉”,使得整个课堂更丰富饱满深刻. 教学环境、问题串和“明暗两线”三位一体,不可分割,强调深度学习的性质:教师引导下的教学,形成了一颗完美的“智慧果”,促进学生发展,实现有意义的学习过程. 所以“启智”课堂教学模式应用的关键就是布局“明暗两线”,设计问题串.

图1 “启智”课堂教学模式架构

3 理论背景

对于布局“明暗两线”,人教版高中数学教材主编章建跃博士指出教学过程要布局明暗两线,明线一般是从内容角度给出的“基本套路”,以明线为载体,在内容中反映出数学的思想和方法,明线中蕴含着暗线. 而对于设计问题串,美国心理学家布鲁纳指出:“教学过程是一种提出问题和解决问题的持续不断的活动,思维永远是从问题开始的.”通过这一系列高质量的问题,帮助学生“亲身”经历知识的发现与建构过程,使学生真正成为教学的主体.

4 实施策略

对于布局“明暗两线”,一般以“事实——概念——性质(关系)——结构(联系)——应用”为明线,以“事实——方法——方法论——数学学科本质观”为暗线. 而对于设计问题串,循环设计“问题——追问”,不仅要问得好而且还讲究串得好,问题需要具有一定的挑战性,循序渐进、逐步深入,能够促进学生自觉地思考,体现深度学习的过程: 让学习真正发生.

5 模式应用

本文以“椭圆及其标准方程”课时为例,具体谈谈“启智”课堂教学模式的应用.“椭圆及其标准方程”是“椭圆”单元的第一个课时,圆锥曲线是学生在过去没有研究过的几何图形,椭圆的概态与性质是圆锥曲线的代表性内容,双曲线、抛物线的内容与它同构,“椭圆”的内容架构、研究过程和思想方法与“直线和圆的方程”基本一致. 与圆的定义一样,椭圆的定义是基于运动轨迹的,其要点是“平面内到两个定点的距离之和为常数的点的轨迹”,设法让学生体验定义所蕴含的完美的数形结合思想,可以全面提升学生对数学的认识水平,形成新的数学学科视角, 提高数学表达的条理性和严谨性,在此过程中,学生的数学抽象、数学建模、数学运算、逻辑推理、直观想象等素养也就得到了提升.

通过本课时的学习,学生能够了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用,经历从具体情境中抽象出椭圆的过程,掌握椭圆的定义及标准方程. 学生能通过观察用平面截圆锥的过程,直观认识截口曲线的形状是圆或圆锥曲线,能通过实例,说明椭圆在生产、生活中的广泛应用. 学生能从画椭圆的过程中抽象出椭圆的几何特征,给出椭圆的定义;能根据椭圆的几何特征建立适当的坐标系,求出椭圆的标准方程,进一步体会坐标法和数形结合、化归与转化等思想. 学生能用椭圆的定义、标准方程解决一些数学问题和简单的实际问题,进一步体会坐标法的重要作用.

本节课的教学环节包括物理环境、虚拟环境和人文环境, 三者共同支撑课堂的顺利进行. 整个课堂教学以“现实背景——曲线的概念——曲线的方程——曲线的性质——实际应用(如图2)”为明线,以“任何问题——数学问题——代数问题——方程求解”为暗线. 问题串包括以下四个主问题及若干追问,四个主问题具体是: 类比直线和圆的方程的研究过程,你认为我们应按怎样的路径研究圆锥曲线. 取一条定长的细绳,把它的两端拉开一段距离,分别固定在图板的两点,套上铅笔,拉紧绳子,移动笔尖,画出的轨迹是什么曲线. 有了椭圆的定义,接下来要合理地建立坐标系,推导椭圆的方程,观察椭圆的形状,你认为怎样建立坐标系可使所得的椭圆方程形式简单. 如果椭圆的焦点位于轴上,与的意义同上,那么椭圆的方程是什么? 你能不做具体推导就得出结论吗?

图2 课堂教学“明线”示意图

为了更好地应用“启智”课堂教学模式,鉴于椭圆的几何特征比圆复杂,虽然学生刚刚学过直线和圆的方程,但是对于从哪个角度入手抽象椭圆的几何特征会出现困惑,并且建立合适的坐标系才能得到椭圆的标准方程,这里的“合适”是指充分利用了椭圆的几何特征,特别是对称性,但是学生在这方面的经验不多、意识不强. 在“互联网+”时代,信息技术的广泛应用正在对数学教育产生深刻影响,信息技术是学生学习和教师教学的重要辅助手段,因此本节课充分发挥了信息技术及椭圆教具(如图3)的作用,利用信息技术展示椭圆在现实中的广泛应用,使学生感受学习椭圆的必要性;利用几何画板或小视频演示用平面截圆锥得到圆锥曲线的过程、椭圆的生成过程及例题中点的运动轨迹,一方面可以提高教学效率,另一方面可以帮助学生形成椭圆的直观形象;通过教具画出椭圆,观察作图过程,可以让学生真实地感受到“动点到两个定点的距离之和为常数”这个椭圆的几何特征,为抽象椭圆的几何特征、得出椭圆的定义提供基础.

图3 椭圆教具

“椭圆及其标准方程”这一课时通过一系列引领性、具有挑战性的问题展开,整个课时的设计结合明线布暗线,为学生营造一种开放式的教学环境,最终提升学生的数学学科核心素养,实现人的全面发展(如图4).

图4 “启智”课堂教学设计示意图

“启智”课堂教学模式有很好的可预期的育人成效,在实施过程中,通过布局明暗两线,设计问题串,在主问题和追问的探究与解决过程中,帮助学生树立问题意识,提高问题解决能力,进而优化思维品质,全面提升学生对数学的认识水平,形成新的数学学科视角,培育学生数学学科六大核心素养,进而实现全面发展,达到深度学习的任务与目的: 培育未来社会实践的主人,促进学生作为具体的社会历史实践主体的成长和发展(如图5),落实立德树人根本任务.

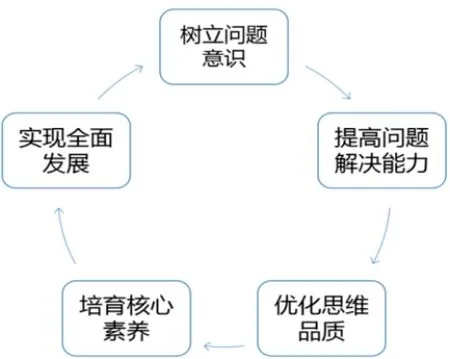
图5 育人成效示意图