聚焦课堂教学,培养核心素养——谈谈如何更好地落实新课标的“三会四基四能”

广东省深圳市龙岗区石芽岭学校(518112) 朱志坚 吴卓婷

目前国内数学教学中,有很多文章都提出了聚焦课堂教学,培养学生的数学核心素养,从而提升教学的有效性,它们介绍的观点、方法也很多. 特别是新版课标出台以后,提到这方面的文章更多了. 但是,紧紧围绕着数学的核心素养:“三会”的文章不多. 近期听了我校吴卓婷老师讲的“整式的加减之合并同类项”数学公开课,感受颇深. 现就根据新课标提出的“三会四基四能”要求,结合本节课的教学过程,进行细细剖析,希望能做到抛砖引玉的效果.

这节数学课的教学过程是:

第一环节: 情境引入. 通过PPT,播放商场(超市)的货物摆放有序图、药店药品摆放有序图,以及偖币罐内有若干枚一角、五角、一元的硬币的图片,设置小问题:“到商场购买零食时,该到哪里挑选? ”“购买感冒药时到哪儿挑选? ”“如何统计多少钱更快捷? ”,进一步提问:“为什么这样做会更有利? ”

这样设置小问题,更有效地引导学生观察并思考现实生活中的问题: 物品的摆放合理性、数字统计的小技巧等等,目的是能有效地应用好所学的数学知识和思维、思想, 更好地服务生活,让人们生活得更方便、更快捷. 在这里,既能贯彻地落实了新课标提出的“会用数学的眼光观察现实世界”,同时还有意识的引导学生应用数学分类讨论的思想,来思考现实生活世界,体现了新课标提出的“会用数学的思维思考现实世界”,更为接下来的“同类项”概念埋下了伏笔.

第二环节: 探索“同类项概念”.

老师通过小游戏:“找朋友”,引导学生对6x、4ab2、-3x、1、0.6ab2、-4、5 这些单项式思考: 谁与谁是好朋友? 请找出来. 鼓励学生自己思考并分类操作,并通过“你是根据什么进行分类的”的问题设置,有意识地引导学生,应用自己的语言说出这样分类的根据:

1. 所含字母相同；

2. 相同字母的指数也相同.

进而如春雨一样,“随风潜入夜,润物细无声”地抛出“同类项概念”: 所含字母相同,并且相同字母的指数也相同的项叫做同类项[1].

接下来,又设置了两个游戏:“找朋友”和“同类项速配”的活动,让学生加强对同类项概念的理解.

其中“找朋友”题目如下:

1) -5x3y2；2) -5a3；3) 12；4) 15zy2x3；5)-125；6)2/3x3y2； 7)-a3；8)x3y2z.

课堂中,老师让小组中基础最差的4 号回答,体现了“基础知识,人人过关”的思想.

另“同类项速配”题目如下:

先判断每一组是否是同类项,若不是的,为前者配一个:

1) 2x2y与-3yx2;2) 2abc与6ab;3) -3pq与2qp;4)-4x2y与5xy2.

在这两个游戏中,特别是在“同类项速配”游戏方面,对学生是有难度的. 在此处,吴老师特意书写了3 种类型题: 1、出现所含的字母相同、相同字母的指数一样,但书写顺序不一致的同类项类型题;2、书写了出现所含的字母不一样的两个单项式的类型题;3、所含字母相同但相同字母的指数不一样的两个单项式的类型题,让学生进行一一辨别、分析,并进行适时、合理的纠正,从而提高学生对“同类项概念”的理解,得出辨析同类项的判别方法:

(1)辨别两个单项式是否同类项,我们只需考虑字母及其指数有关,与单项式的系数无关,也与字母在单项式中的排列顺序无关;

(2)辨别两个单项式是否同类项,我们一定要抓住“两个相同”: 一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可;

(3)千万不要忘记: 几个单独的数也是同类项.

听到此处时,直感告诉我,吴卓婷老师的教学基本功非常扎实,现正有计划、有步骤地实施,李希贵老师提出的“三讲三不讲”教学方法:“讲易错、易混、易漏知识点[2].”从而能轻松地突破了教学难点——找出同类项,更好地培养孩子的“火眼金晴”,提升了学生的辨析能力,进而避免学生在解合并同类项的题目时,在第一个步骤: 找同类项不出差错,确保百分之百正确.

这种让学生主动参与寻找“同类项概念”的数学活动,有力地培养了学生观察问题的能力,进而提升学生发现问题、提出问题、分析问题和解决问题的能力,全方面地提升学生的数学素养.

第三环节: 典例解析.

老师给出了两道提高应用题,加强学生理解、巩固“同类项概念”. 题目如下:

(1)在6xy-3x3-4x2y-5yx2+x3中没有同类项的项是____;

(2) 如果2a4bn+1与-4amb3是同类项, 则m=____,n=____;

这两题都是不能用直接观察法得出来答案的,要考学生的“慧眼”,特别是第2 题,综合运用了“同类项概念”和“方程”,是历届考试中一道中等题目,要求对“同类项概念”非常娴熟. 老师在这儿,充分利用了“小组合作”的方式,让小组的同学相互交流、讨论,特别是让成绩好的1、2 号带领本组的同学进行探究,让学生们充当小老师,实施“生生教学”的方法,充分调动了学生学习数学的兴趣和积极性,从而增浓了课堂学习氛围,也让更多学生理解、掌握好数学知识.

这一环节的教学,既能加深了学生对基础知识——“同类项概念”的理解,又进一步地提高学生的分析问题和解决问题的能力,更方便地掌握好数学知识,同时,在学生的能力培养方面,很好地做到“点动成线、线动成面”的效果,提升了教学质量.

第四环节: 合并同类项.

教师先从幼儿时期的知识引出:

2 个苹果+3 个苹果=? 个苹果.

若将“苹果”换成字母x,又如何表示? 列等式表示.

5 个西瓜-2 个西瓜=? 个西瓜.

若将“西瓜”换成字母a2bc,又如何表示? 列等式表示.

另:“苹果”与“西瓜”能合并吗?

从而引出合并同类项概念: 把同类项合并成一项叫做合并同类项[3]. 同时,还鼓励学生从等式的左右两边的观察、比较中,发现了什么,并大胆猜测. 引导学生发现合并同类项的计算简易方法: 只要整式的加减运算中,出现同类项,我们便可将这些同类项合并成一项.

根据乘法对加法的分配律,对上述题目进行解释、验证,同时还增加了两道可运用乘法对加法的分配律,进行合并同类项的题目:

(1)-xy2+3xy2;(2)7a+3a2+2a-a2+3.

这样的练习,加深了学生对刚才猜测到的合并同类项的方法进行验证,从而自己去归纳、总结“合并同类项的步骤”:一找二移三合并.

这一环节的教学,更加深入地体现了新课标提出的“发展运用数学知识与方法发现、提出、分析和解决问题的能力(简称‘四能’)”,也呈现了有效课堂教学中老师整合教材的“整合度”,和学生大胆想象,解放思想、发言自由的“自由度”

第五环节: 牛刀小试.

这一环节主要是让学生自己运用合并同类项法则、步骤进行解题,是对整式的加减法之合并同类项的巩固训练,题目设计呈螺旋式地上升,难度由台阶一样,一层一层地,由浅入深,加深了对合并同类项步骤的理解、领悟、消化,是一个学以致用的环节.

但是,老师对做这些题目的同学进行了巧妙的安排: 对小组中的3、4 号学生,自己任选四道题中的一题,在教室的墙壁书写,完整地展示出自己掌握的解题步骤和方法,也算是完整地展示出自己当堂掌握知识的能力. 而小组中基础较好的1、2 号学生在做完所有的题目后,还要对墙壁上题目进行现场批改.

我们要贯彻有效课堂教学中提出的“参与度”和“展示度”: 学生全员参与学习过程,并在过程中,学生都展示出自己的解题思路和当堂学习的效果,呈示出自己的才华和能力,同时在展示过程中,克服畏羞心理,勇于暴露出自己的缺点和不足,敢于改进. 当然,也体现出苏霍姆林斯基提出的“首次学习教材时,能看到每个学生的脑力劳动成果[4].”

第六环节: 拓展延伸.

题目如下:

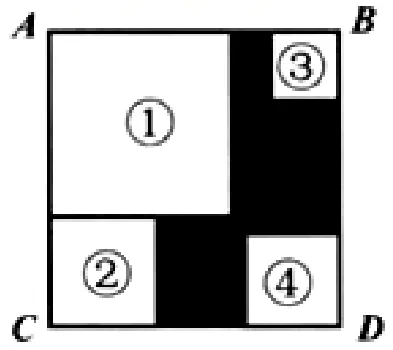
如下图,一个大正方形的四个角落分别放置了四张边长大小不一样的正方形纸片,其中①, ①两张正方形纸片既不重叠也无空隙. 已知①号正方形边长为a, ②号正方形边长为b,则阴影部分的周长是____.

这一道题对学生而言, 是富有挑战性, 是应用所学过的数学知识, 通过建模的思想来解决现实生活中的问题, 它充分体现了数学是来源于生活,又服务于生活, 很好地贯彻落实了新课标提出的“会用数学的语言表达现实世界”.

纵观整节课的教学过程,给人感觉像进入一个寻宝密室,每个人都是从不知的入口进去,探索至略知,努力奋斗、拼博,最终寻到宝矿——通过合并同类项来进行整式的加减. 同时还在探索的过程中,亲身体验到自己只要“跳一跳就能摘到果子”,展示出自身拥有较强的学习能力和探索能力,收获成功学习知识的喜悦感.

这节课也充分地体现了李镇西老师提出的“好课堂标准”:“所谓‘好课堂’,就是‘有趣’加‘有效’[5].”也体现了“数学教育的方向开始强调‘知’的过程,从‘知’走向‘智’[6],”更是将新课标提出的“三会四基四能”接入地气,将新课标的目标扎扎实实地落实到位.

附: 1.“三会四基四能”中的“三会”,指的是:

(1)会用数学的眼光观察现实世界;

(2)会用数学的思维思考现实世界;

(3)会用数学的语言表达现实世界[7].

2.“三会四基四能”中的“四基四能”,指的是:

课程目标以学生发展为本,以核心素养为导向,进一步强调学生获得数学基础知识、基本技能、基本思想和基本活动经验(简称“四基”),发展运用数学知识与方法发现、提出、分析和解决问题的能力(简称“四能”),形成正确的情感、态度和价值观[8].