脚手架理论在中职数学教学中的应用

【摘要】本文基于脚手架理论的内涵分析，论述脚手架理论对促进中职生数学学科核心素养的作用，提出运用脚手架理论开展中职数学集合教学的策略：分层设定目标，搭建目标脚手架，强化培养学生的探究意识；创设真实的教学情境，搭建学习情境脚手架，促使学生能力实现递进式发展；关注学生的情感体验，注重知识的反思回溯，搭建思想进阶提升脚手架等。

【关键词】脚手架理论 学科核心素养 中职数学教学 集合

【中图分类号】G63 【文献标识码】A

【文章编号】0450-9889（2023）20-0084-04

《中等职业学校数学课程标准（2020年版）》（以下简称数学课标）指出，中职数学教师在教学时要准确把握教学要求、做好教学设计，合理运用各类教学资源，推动教学方式方法改革；要根据课标中的学业质量要求，重点考核学生运用知识发现与解决实际问题的能力，促进学生学科核心素养的发展。数学课标对促进学生数学学科核心素养发展做了明确阐述，这给中职数学教师推动学科教学改革指明了基本方向。在此背景下，中职数学教师应该从优化教学资源配置、创新教学理念、改进教学方法等方面着手，探索促进数学教学改革、发展学生学科核心素养的有效路径。为此，笔者尝试通过搭建教学“脚手架”的方式，推进“支架式教学”方法在中职数学教学中的应用，取得了较好的实践探究效果。

一、脚手架理论的内涵

脚手架原是指工程建设中为推进施工进度、确保高层建设而搭建的施工平台，由于其具有组合与递进的特点，因此这一概念得以被引用到教育教学领域。教育领域脚手架理论的提出，最早可追溯到1976年，美国教育学家布鲁纳从建筑行业中得到启发，首次提出了“脚手架”的概念，并进一步将其解释为“支架式教学”。脚手架理论是以苏联心理学家维果斯基的“最邻近发展区”理论为基础和模板。维果斯基认为，儿童要解决的问题和儿童原有能力间可能存在差异，但儿童能够在教师帮助下通过学习消除这种差异。这个差异就是“最邻近发展区”。根据维果斯基的理论，布鲁纳认为在帮助儿童走向“最近发展区”的过程中，教师作为更富有经验、具有更强认知能力的长者，通过搭建脚手架（或称为“支架”）的方式，为学生铺设进步的阶梯，可以有效提高学生的学习效率，这也符合学生的认知心理特性。

具体而言，脚手架理论认为，当学生开始学习新的概念时，由于学生的知识储备、经验能力等尚欠缺，因此需要教师的主动支持，在教师的帮助、指导下展开有效的学习。在教师支持和帮助的过程中，学生通过主动思考、解决问题，从而获得新知识、新技能，不断发展和提高自身的学习能力。在学生开展学习的整个过程中，教师就像建筑行业中的脚手架，起到支持和指导学生学习、帮助学生发展进阶的作用。

基于这样的理解和认知，笔者近年将脚手架理论引入中职数学教学，进行了长时间的教学实践研究。通过实践研究，笔者认为脚手架理论在中职数学教学中的应用，有助于教师开阔专业视野、丰富专业知识储备、转变教育教学理念、改进教育教学方法，也有利于学生养成探究意识和提升知识迁移应用能力。尤其是就目前的实际情况而言，部分中职学校的数学学科教学仍然存在重分数轻技能、重理论轻应用的问题，这可能会阻碍学生数学思维的发育和发展，同时也不利于在其他专业教学中渗透数学知识，从而在一定程度上降低学生的专业学习效果。在这种情况下，在中职数学教学中引入脚手架理论，就具有重要的现实意义。

二、脚手架理论对促进中职生数学学科核心素养的作用

数学课标提出，中职数学学科核心素养主要包括数学运算、直观想象、逻辑推理、数学抽象、数据分析和数学建模等六个方面。长期以来，在如何培养学生学科核心素养方面，有不少中职数学教师感到困惑，困惑点主要是如何有效开展学科核心素养培养工作。在实践探究过程中，笔者发现脚手架理论能够有效解决这一问题。

（一）有利于从建构主义视角促进学生数学学科核心素养的发展

在教学过程中，教师可以借助脚手架理论，从建构主义视角对数学知识进行科学分层，让学生在完成各层次学习任务的过程中，促进自主学习能力的提升和学科核心素养的发展。在具体教学中，教师首先要科学设定分层目标，然后根据目标合理筛选、整合、安排分层教学内容，设计分层教学任务，帮助学生搭建起通向深度学习的脚手架，接着根据学生的学情和需求布置学习任务，以学习任务驱动学生积极参与学习、探究问题，从而有效落实核心素养的培养。要注意的是，在为学生搭脚手架、实施分层教学的过程中，教师要始终坚持以学生为中心的原则，任务为学生而设、活动为学生而开、支架为学生而建，切不可脱离学生学情随意开展教学。

如在中职数学基础模块“集合的表示法”这一内容的教学中，教师可以通过创设有趣味的问题情境，激发学生的学习兴趣，为学生深入学习这一知识搭建起脚手架，有效引导学生学习、探究和分析集合的表示方法，并在逐层解决问题的过程中掌握概念、厘清范围，最后形成全面认知。为此，笔者在具体教学中设计了以下六个具有层次性的学习问题：①小于7的自然数有哪些？②中国古代的四大名著是哪几部？③奥运会的田径比赛包含哪些小项目？④方程式x2=x有哪些实数根？⑤方程x2-3x+2=0有哪些实数解？⑥以上问题涉及的数据，与我们今天学习的“集合”有什么关系？这几个问题既有数学方面的问题，也有文学、体育方面的问题，而且与学生的学习、生活比较贴近，能够有效激发学生的学习欲望。此外，在解决这些问题的过程中，学生逐渐对“集合”形成了客观、具象的认识，初步掌握了集合的表示方法，发展了逻辑推理、数学抽象、数据分析等数学学科核心素养。在整个教学过程中，层次性学习问题就是助推学生学习的脚手架，教师就是搭脚手架的人，通过借助脚手架，笔者顺利落实了学生数学学科核心素养的培养。

（二）有利于为学生数学学科核心素养进阶鋪设路径

只有教师正确认识脚手架在推进学生核心素养进阶、拔升过程中的功能和意义，积极探索将脚手架理论常态化运用于数学学科日常教学的有效路径，才能深入发展学生的学科核心素养。如，在日常教学中，教师可以根据学生实际设计探究性学习项目和实践任务，并以这些项目和任务为脚手架引导学生通过合作探究、询问教师等方式开展学习，使脚手架理论充分融入学生的日常学习，从而持续促进学生学习能力、学科核心素养的发展。教师还要注重学生与企业的互动实践、学生与社会的联系，将企业实习、社会实践作为深入开展教学活动的抓手，作为搭建学生学习脚手架的“基底”，让学生在真实的情境中学习、体验、感悟，最终促进数学运算、直观想象、逻辑推理等数学学科核心素养的发展。

由此可见，将脚手架理论融入中职数学教学，并与学生学科核心素养培育相结合，能够产生积极的教学效果。因此，教师在教学中要始终坚持由易到难、由浅及深的教学思路，借助学习脚手架引导学生不断深入学习基础知识和技能、开展企业和社会实践，促使学生将課堂所学知识迁移运用于解决生活中的实际问题，才能有效实现全面发展中职生数学学科核心素养的目标。

三、脚手架理论在中职数学集合教学中的应用策略

（一）分层设定目标，搭建目标脚手架，强化学生探究意识的培养

过去，由于部分教师存在“数学学科只要让学生会算、懂算”的观念，所以中职数学教学普遍存在以理论知识讲授为主的现象。这种教学观念和教学方法带来的消极后果，是学生虽然能够掌握一些基础的运算技巧，但一旦碰到比较复杂的运算问题，就会感到无从着手。其中一个突出的表现是，分层教学目标难以科学设定，层次性学习难以有效推进，学生的探究意识难以得到发展。鉴于此，数学教师可以借鉴脚手架理论，通过科学设定分层目标为学生搭建学习脚手架，促使学生深入探究知识，并学会运用相关知识解决问题，从而不断发展学生的逻辑推理、数学抽象、数据分析和数学建模等数学学科核心素养。

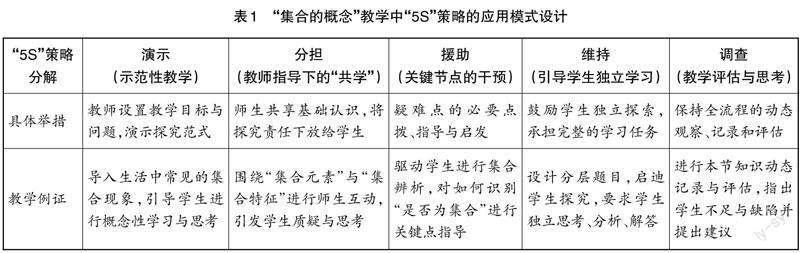
在具体教学中，教师首先要对学生学情进行调研，科学分析学生的学习能力、学习水平；然后要对相关知识点进行细化分解，再由浅入深、由粗及细地设计教学维度和分层教学目标；接着要根据不同的维度和目标设计探究性学习任务，为学生搭建起学习脚手架，从而不断促进学生探究意识和探究能力的提高。以“集合的概念”这一内容的教学为例，教师可在教学中运用“5S”策略有效分解教学目标，为学生搭建学习脚手架，帮助学生在真实的教学情境中由浅入深地学习知识和技能，在“踏阶而上”的过程中提升自身的综合能力，从而取得递进式的教学效果（如表1所示）。

由表1可知，“5S”策略包含演示、分担、援助、维持、调查五部分，这是一个逐层递进的教学过程，也是一种有助于促进学生学习的脚手架，目的在于引导学生拾级而上，形成探究性学习的意识和能力，不断提高学习效果。以“集合的概念”这一内容的教学为例，笔者搭建学习脚手架的具体做法如下。笔者首先出示探究问题，对问题做适当讲解，然后根据问题与学生共同开展探究性学习，在学生开展探究学习过程中进行适当点拨，并针对存在问题提出解决建议。在此基础上，笔者让学生独立探究“集合的特征”（即如何辨析集合概念与现象）这一问题，引导学生尝试总结集合的概念和集合的辨析方法，从而巩固和提高学生的自学能力。最后，笔者先让学生通过自评、互评的方式，尝试总结在整个学习中自己遇到的难题和问题，再对学生的学习进行总结性评价，并给学生提出解决问题的建议和意见。

在教学中，笔者借助应用题展现集合的特征，重点讲解集合的确定性、无差异性与无序性等特性，让学生深刻理解集合的含义和基本特征。如在讲解集合的“确定性”时，笔者首先举出“个子高的女生”“比较小的杯子”两个反面例子，引导学生尝试表述这两个例子的集合。当学生发现无法进行表述时，学生认识到只有确定性因素才能构成一个集合。又如在讲解集合的“无差异性”时，笔者设计了这样一道例题：有两个集合A={1，2，3，4}，B={3，4，5，6，7}，把这两个集合合并起来后得到怎样的新的集合？新的集合与原来两个集合有什么相同之处和不同之处？根据笔者的引导，学生很快合并出了新的集合{1，2，3，4，5，6，7}，并比较分析出三个集合的相同点和不同点，从而理解了集合的无差异性。

在教学过程中，笔者采取“5S”教学策略，首先展示案例进行演示教学，作为引导学生进入学习的脚手架，让学生初步了解集合的概念和特性；然后通过设计探究性问题，作为学生开展进阶学习的脚手架，引导学生自主学习、合作探究，让学生在解决问题的过程中，深入理解集合的定义，以及辨析集合的方法；最后通过调查与评估，了解学生掌握概念和知识的程度，并针对学生存在的疑惑和问题，提出解决建议和办法，这是帮助学生实现螺旋上升的脚手架。值得一提的是，并非“5S”策略的每一个步骤都要体现在教学中，教师要根据教学实际所需选择合适的策略，避免出现“为策略而策略”的情况。

（二）创设真实的教学情境，搭建学习情境脚手架，促使学生实现递进式发展

建构主义理论认为，在教学中突出学生的主体地位，驱动学生以自我为中心进行主动学习、积极探索，这样的教学方式相较于由教师讲授、由教师安排的教学方式，能取得更好的教学效果。而搭建学习脚手架的本质目的，就是通过创设生活化教学情境的方式，为学生营造熟悉、活泼且充满温度的学习氛围，调动、激发学生的主观能动性，让学生在轻松愉悦的氛围中发散思维、探究新知，从而不断提高课堂教学有效性，促进学生学科核心素养的发展。

如在“集合的表示法”这一内容教学中，笔者通过设计生活化问题创设学习情境，为学生搭建学习集合知识的脚手架。笔者设计了这样几个生活化的集合问题：中国所有直辖市的集合、地球几个大洋的集合、教室内所有椅子的集合、所有三角形的集合、1—100自然数的平方的集合。上述几个问题涉及中职生比较熟悉的直辖市、椅子等生活事物，能够有效拉近学生与问题的距离，激发学生思考与探究的兴趣。

通过上述问题的导入，教师可以让学生从直观的生活现象入手，思考集合应该如何描述，进而在思考、分析中明确集合的表示方法。通过分析，前两个集合可以采用“列举法”进行表示：我国有北京、上海、天津与重庆四个直辖市，世界上有太平洋、大西洋、印度洋和北冰洋四个大洋。而关于第三个集合，学生可以通过数教室里的椅子得出。这几个问题都与学生的学习或生活相关，既能够有效激发学生的探究兴趣，又能让学生有效掌握表示集合的方法。在笔者的引导下，学生通过探讨、思考，尝试总结出集合列举法的适用条件：①有限集合且元素不太多；②有较多元素的集合但存在一定规律，可以用省略法表示；③有规律的无限集合。为了进一步巩固学生所学知识，笔者让学生尝试运用这一方法表示“所有三角形的集合”“1—100自然数的平方的集合”这两个集合。

在教学过程中，笔者通过设计一连串问题创设生活化教学情境，以问题为抓手、以递进思考为依归，引导学生对集合的表示方法进行研究，使学生获得對概念和解答方式的认知，为学生搭建起进阶学习的脚手架，提高学生的知识迁移应用能力。

（三）关注学生的情感体验，注重知识的反思回溯，搭建思维进阶提升脚手架

学生是学习的主体，因此在搭建学习脚手架的过程中，教师一方面要关注学生的学习情感体验，改变单纯输出知识的教学方式，丰富教学的多样性意蕴；另一方面要注重驱动学生积极“回头看”，养成对知识点的温习、回溯和反思意识。无论是数学游戏、娱乐活动还是课堂互动探究，都是赋予学生更大自由度的教学方式，目的在于释放学生的天性和热情，促使学生独立学习与深度探究。在此过程中，教师要发挥“指挥者”作用，搭建脚手架，提供辅助与指导，确保学生的知识反思与回溯达到预期目标。

在课堂教学中，教师通过游戏化教学方法优化学生的情感体验，用生活化的活动使学生对数学知识形成多维度认知，有利于提高学生的学习效率。如在讲解补集的知识时，笔者便将“狼人杀”游戏与补集的运算方法相结合，让学生在玩游戏的过程中理解什么是补集，并掌握补集的运算方法。这种通过游戏增强学生的学习情感体验的教学方法，能够有效搭建起学习的脚手架，引导学生围绕知识要点、疑难点进行反思与回溯，最终能够有效促进学生能力的提高与核心素养的发展。

又如，在“集合的运算”教学结束后，教师引导学生温习、反思，重点抓住疑难点和易错点进行“回头看”，驱动学生自主对相关知识点进行二次探索，巩固知识结构、丰富知识体验。为了更好地引导学生开展课后学习，笔者设计了“我们班爱好篮球与音乐的男生”“班内数学和语文成绩都比较好的学生”“上个学期获得过奖状的男生和女生”等学习任务，让学生运用交集、并集、补集的知识完成这些知识点的学习，学生在相互问询、交流、探讨的过程中，既巩固了课堂所学，又发现了知识与日常生活的联系，能够有效激发学生的学习兴趣。通过引导性学习任务的设置，让学生形成知识回溯的意识和能力，进而在运用集合运算知识和技能的过程中优化反思体验，增强知识应用黏性。

综上所述，基于学生中心论和建构主义理论的脚手架教学方法，能够有效激发学生的学习兴趣，帮助学生在学习脚手架的支持下开展深度学习，从而促进学生学科核心素养的全面发展。而要想充分发挥脚手架理论的育人功能，教师应扮演好“指挥家”“驱动者”的角色，只有科学合理设定教学目标，细化教学策略与步骤，尊重学生的个体差异与身心特点，促使学生独立学习、深入探究、关照现实、体察生活，才能不断促进学生的全面发展。

参考文献

［1］韩加增.中职数学分层教学模式下生活化策略的探索研究［J］.现代职业教育，2021（2）.

［2］赖小平.要为学生的猜测搭好思维的“脚手架”［J］.实验教学与仪器，2018（7）.

［3］常鑫海.中职数学教学中存在的问题及解决策略［J］.甘肃教育，2020（2）.

［4］张晓方.中职数学教学中学生思维能力的培养［J］.当代教育实践与教学研究，2020（11）.

［5］冯慧明.中职数学课堂融入核心素养的教学探究［J］.课程教育研究，2020（10）.

作者简介：龙波（1981— ），广西柳州人，讲师，主要研究方向为中职数学教学。

（责编 蒙秀溪）