对一道竞赛题及其逆命题的探究

许爱瑛 (陕西省咸阳中学 712000)

2020年马其顿数学奥林匹克竞赛中有一道不等式证明题:

文[1]用三角换元法给出了证明,但证明过程比较复杂.如果注意到不等式①两边的结构,联想到均值不等式,则可获得一种十分简单的证明．

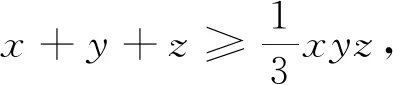
将问题1推广,得到下列结论:

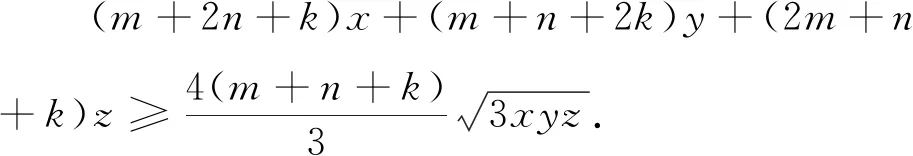
证明 由已知条件及均值不等式,得

9(m+n+k)=mxy+nyz+kzx≥

解得xk+mym+nzn+k≤32(m+n+k),所以

(m+2n+k)x+(m+n+2k)y+(2m+n+k)z

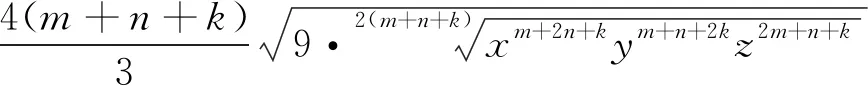
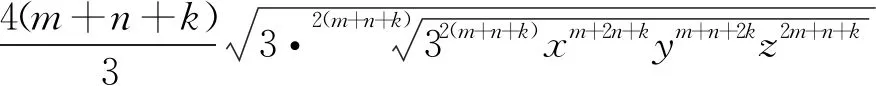
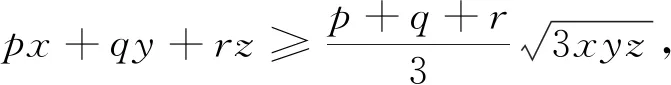
如果将推广1及其证明中的3换为正实数p,那么类似地可以证明:

推广2正实数x,y,z,p及正整数m,n,k满足mxy+nyz+kzx=p2(m+n+k),求证:(m+2n+k)x+(m+n+2k)y+(2m+n+k)z≥

如果考虑将问题1的已知条件和所证不等式互换位置,那么可以得到如下逆命题:

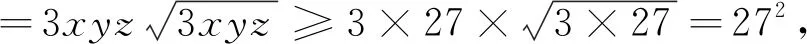
将问题2推广,得到下列结论:

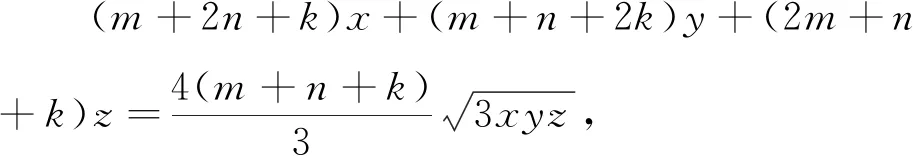
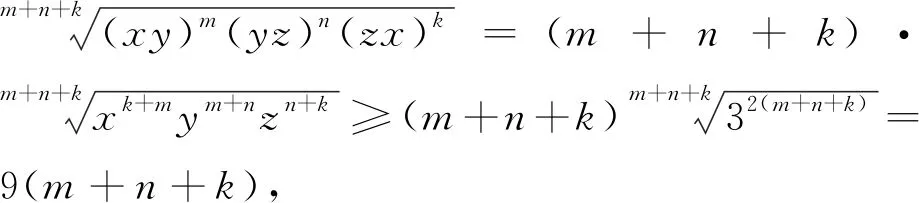
类似地,可以证明:

上面对竞赛题及其逆命题的推广,只是将已知条件和要证明的不等式中变量的系数进行了拓展,但不等式等号成立的条件仍然是x=y=z,对于其他取等号的条件,不等式会怎样变化呢?留给有兴趣的读者去思考吧．