建立函数模型教学中的一个误区分析*

刘 嘉 (北京市朝阳外国语学校 100012)

数学建模素养是新一轮课程改革中提出的六大学科核心素养之一,在2017年版高中数学课程标准中,详细阐述了数学建模的内容,并提出了具体的课时要求和教学要求．在此背景下,越来越多的教师开始在课堂上开展数学建模教学．但笔者在参加一些教研活动时,发现部分教师对建立函数模型的教学认识有一些误区;在指导一些学生参加数学建模竞赛时,发现部分学生在建立函数模型时也存在相同的误区．

1 案例1:弹簧振子位移和时间关系的建模

某次教研活动,一位教师上了研究课“三角函数模型的应用”．

1.1 课堂实录片段

师:某弹簧振子在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如表1．试根据这些数据确定这个振子的位移关于时间的函数解析式．

表1 弹簧振子位移与时间对应数据表

师:请同学们描绘出这些数据的散点图,看看像什么函数的图象?

生甲:我们组绘制的散点图如图1,观察散点好像分布在一个三角函数图象上,于是我们组用y=Asin(ωt+φ)进行拟合,得到这个振子的位移关于时间的函数解析式是y=20.25sin(10.51x-1.58)+0.12(图2)．

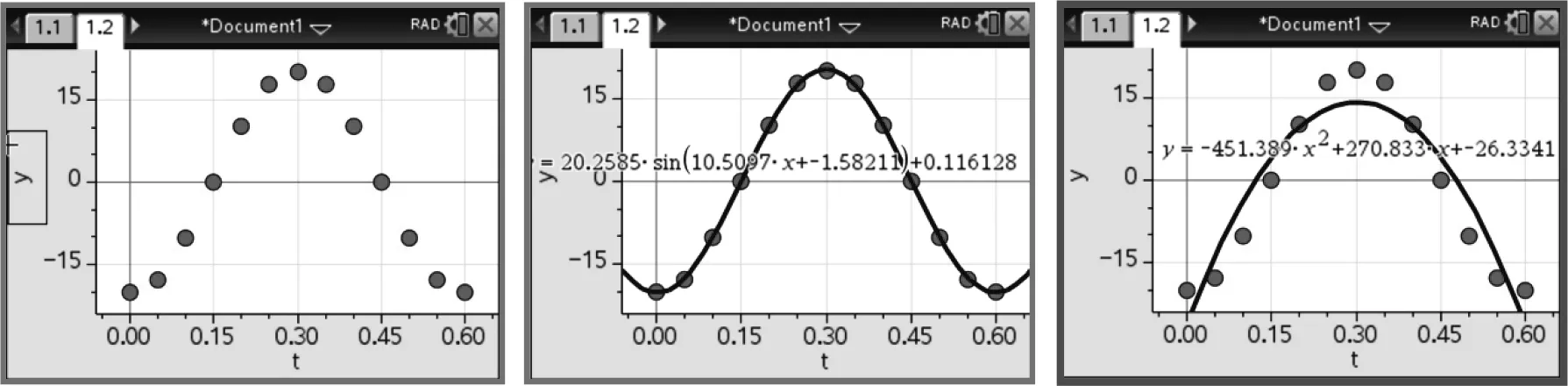
图1 振子的位移关于时间散点图 图2 三角函数模型拟合 图3 二次函数模型拟合

生乙:我们组观察散点好像分布在一个二次函数的图象上,所以选择用二次函数y=ax2+bx+c进行拟合,得到的解析式是y=-451.39x2+270.83x-26.33(图3)．

师:同学们讨论一下,哪个模型更好呢?

生乙:我们觉得甲组同学的模型更好,因为他们的散点基本都分布在函数图象上,而我们组的散点跟函数图象并不完全重合．

生丙:我们组进一步绘制了两种函数模型的残差图(图4、图5)．可以发现,用三角函数模型拟合时,残差几乎分布在x轴上,而用二次函数模型拟合时,残差分布在x轴两侧一个宽度约为12的带状区域内．通过对比,我们认为选用三角函数模型来描述这个振子的位移关于时间的函数关系更好．

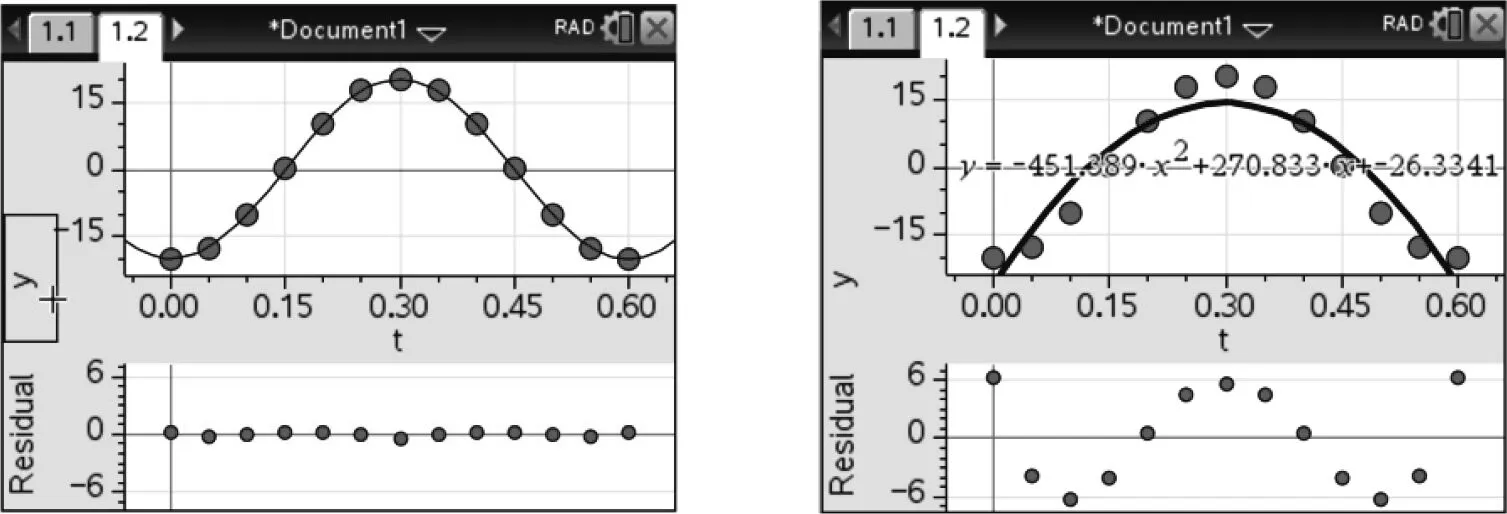
图4 三角函数模型残差图 图5 二次函数模型残差图

师:同学们的讨论非常精彩,我们可以通过绘制残差散点图或计算残差平方和来更精确地检验哪种模型更好．一般地,如果残差平方和越小或者残差散点图分布的带状区域越窄,我们可以认为这个模型越准确．

1.2 点评

对于在“振子的位移关于时间的函数解析式”建模过程中,为什么选择三角函数模型,教材上是这么说的:“振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移y随时间t的变化规律可以用函数y=Asin(ωt+φ)来刻画．”教材的处理思路是首先通过物理原理,确定需要用三角函数模型来刻画振子位移随时间变化的规律,然后再通过表1中的数据,来确定模型中A,ω,φ等参数．笔者认为教材的处理方式更合理．

2 案例2:燃气旋钮角度和燃气用量关系的建模

2.1 课堂实录片段

这是2021年部级精品课“数学建模:建立函数模型解决实际问题”中的一个片段,该网课可在国家基础教育精品课网站观看．教师首先介绍实际背景,作为日常必需品之一的天然气是清洁能源,很多家庭的一日三餐都要使用天然气,但是我国天然气大部分依靠进口,时常出现供应紧张的局面,节约用气刻不容缓．紧接着提出要研究的问题:“如何使用燃气灶最省气?”之后教师引导学生分析影响燃气灶用气量的因素有哪些,分析选定燃气旋钮旋转的角度为自变量,烧开一壶水所需的燃气量为因变量,通过研究二者的关系来探究如何操作能够使烧开一壶水所需的燃气量最少．

明确研究问题后,教师引导学生开始收集数据,得到表2．

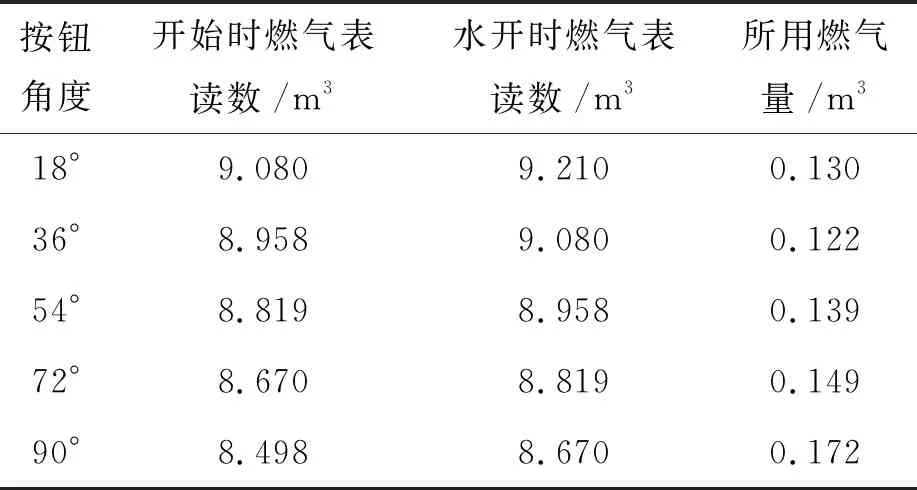
表2 燃气旋钮处于不同位置时烧开一壶水所用燃气量

之后,将表2中数据整理为散点图(图6),教师引导学生观察,散点近似分布在一个二次函数的图象上,因此可以考虑使用二次函数y=ax2+bx+c进行拟合．选取三对数据(18,0.130),(36,0.122),(90,0.172)代入,解得y=1.903 3×10-5x2-1.472 2×10-3x+1.503×10-1．

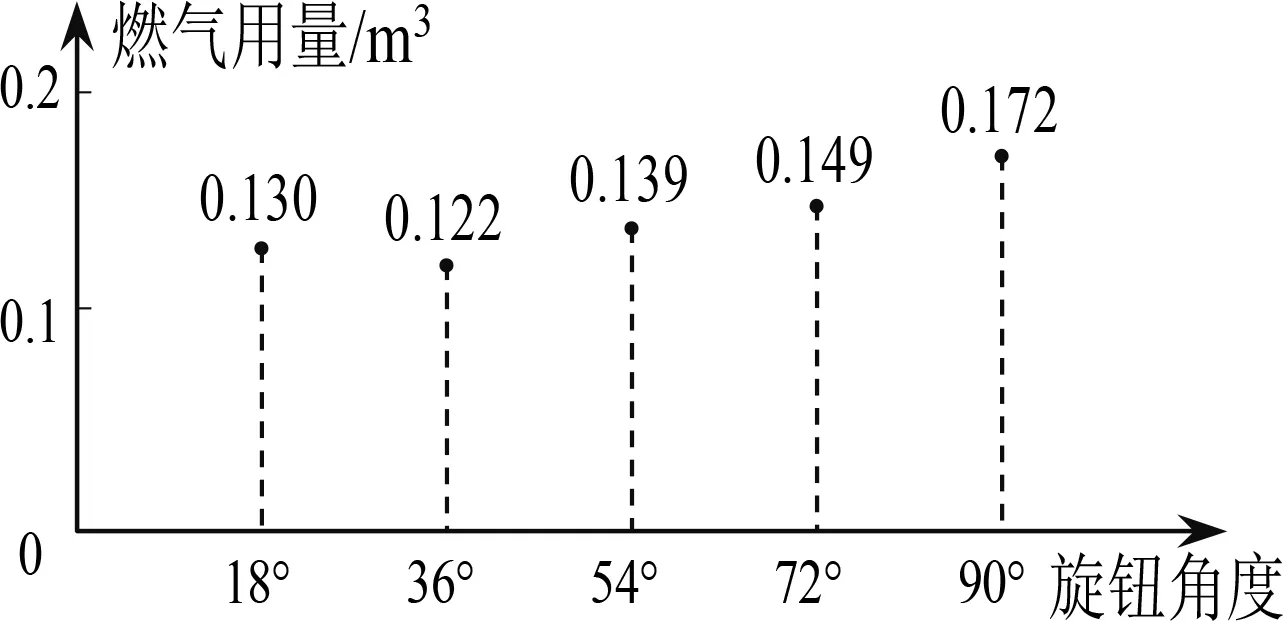
图6 燃气旋钮角度与燃气用量散点图

2.2 点评

本课是一节水平非常高的建模教学课,教师引导学生经历了选题、确定变量、搜集数据、整理数据、建立模型、模型评价、模型应用等建立数学模型解决实际问题的全过程,所研究的问题“节约燃气”有较强的社会意义,并且也贴近学生生活．但是在建立模型的过程中,根据散点近似分布在一条抛物线上而选择用二次函数进行拟合略有不妥．如果仅仅从这5个散点的分布来选择模型,那么用4次多项式函数进行拟合,能够使得这5个散点都精确地分布在这个函数的图象上．笔者还是建议采用类似于教材的处理方式,通过对燃气旋钮角度和燃气用量内在机理的分析来确定选用何种函数模型,之后再根据搜集到的5组数据确定模型中的参数．

3 建立函数模型教学中的误区分析

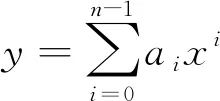
4 建立函数模型教学中的改进策略

4.1 通过分析变量间内在联系,确定模型

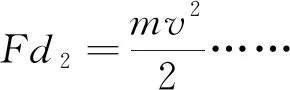
4.2 直接给出变量间内在联系,确定模型

如果两个变量间的内在联系难以借助学生已有知识进行分析,那么教师在教学中,可以选择直接给出模型,由学生根据收集到的数据来确定模型中的参数．比如“案例1”中提及的人教A版教材对弹簧振子的位移和时间关系的处理,就是直接给出模型y=Asin(ωt+φ),然后由学生根据相应数据确定A,ω,φ等参数的值．教材中还有许多类似的例子,又比如必修一第四章第五节例3中,研究人口增长模型,亦是直接给出了马尔萨斯提出的模型y=y0ert,然后给出我国1950—1959年的人口数据,请学生确定模型中参数y0,r等．

4.3 定性分析变量间内在联系,确定模型

如果两个变量间不存在明确的内在联系,或者虽有内在联系,但是难以分析,此时只能退而求其次,定性分析二者间关系,结合收集到的数据进行拟合建模．教材上亦有一些例子,比如人教A版必修一数学建模活动中,探究“茶水温度随时间的变化模型”,通过观察散点的分布规律,发现散点呈下降趋势(图7),那么这些散点近似分布在直线上还是抛物线上或者是其他什么曲线上呢?教材中通过定性分析,指出“茶水温度降至室温就不能再降”这一事实,最终选择用y=kax+25这一函数模型进行拟合．又比如人教A版必修一第五章三角函数模型的应用中探究“港口水深随时间的变化模型”,通过观察散点分布规律(图8),结合“港口水深随时间周期性变化”的特点,选择用y=Asin(ωt+φ)+h这一函数模型进行拟合．

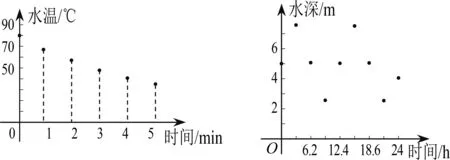
图7 茶水温度随时间变化散点图 图8 港口水深随时间变化散点图

5 结论

建立函数模型解决实际问题一定要抓住事物的本质,尽可能地分析各变量间的内在联系,根据它们的内部机理去选择合理的模型．如果内部机理不明,那么可以通过收集的数据绘制散点图,观察散点分布规律结合对变量间相互影响的定性分析来选择函数模型．尽量避免单纯依据散点近似分布在何种曲线上就选择何种模型,亦不能绝对地认为残差平方和越小,模型就越好．高中数学建模教学中,教师需要引导学生根据问题的实际背景、建模的目的等综合因素,来选择合理的模型,通过具体案例让学生体会数学建模的一般过程,积累数学建模经验,提升数学建模、数据分析、数学抽象、直观想象、逻辑推理、数学运算等学科 素养．