多题一图 变幻无穷
2023-09-10高亢
高 亢
(大庆第二十三中学)
在数学问题中,经常会出现“多题一图”的现象,即不同的题目,在运用数形结合思想解题时会构建同一个图形,虽然这些题目各不相同,解题思路不尽相同,但题目之间却存在着某种必然的联系,本文对此作些探讨,供大家参考.
引例已知x1是方程x+lgx=3的一个根,x2是方程x+10x=3的一个根,则x1+x2=________.
解析将已知的两个方程变形可得lgx=3-x,10x=3-x.令f(x)=lgx,g(x)=10x,h(x)=3-x,画出它们的图像,如图1 所示.记函数f(x)=lgx与h(x)=3-x的交点为A(x1,y1),g(x)=10x与h(x)=3-x的交点为B(x2,y2).由于f(x)=lgx与g(x)=10x互为反函数,且直线y=3-x与直线y=x垂直,所以A(x1,y1)与B(x2,y2)两点关于直线y=x对称.
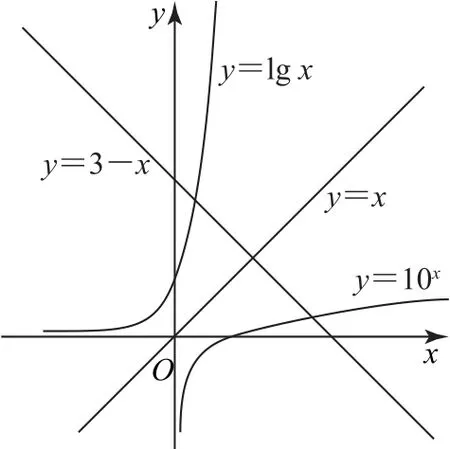
图1
点评本题将方程问题转化为函数问题,注意到f(x)=lgx与g(x)=10x化为反函数,它们的图像关于直线y=x对称,于是利用图像的对称性即可求出直线y=-x+3与两个函数图像的交点的横坐标之和.
引例解答中的这个图像极具代表性,笔者发现,在许多相类似的问题中都会出现.
变式1已知a>1,方程ex+x-a=0与lnx+x-a=0的根分别为x1,x2,若则m的取值范围为_________.
解析方程ex+x-a=0 的根,即y=ex与y=a-x图像交点的横坐标,方程lnx+xa=0的根,即y=lnx与y=a-x图像交点的横坐标.易知y=ex与y=lnx的图像关于直线y=x轴对称,如图2所示.y=a-x与y=x交点为所以x1+x2=a,所以
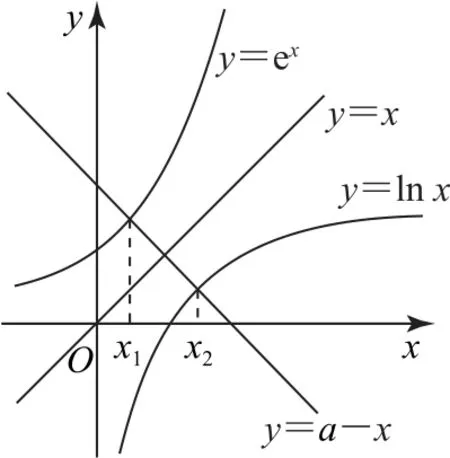
图2
点评解答本题的关键是将m表示为关于a的函数,再利用图像法,根据图像的对称性得到x1+x2=a,本变式是引例的延续.
变式2(多选题)已知函数f1(x)=x2+3x-5(x>0),f2(x)=e2x+x-2,f3(x)=lnx+2x-4的零点分别为x1,x2,x3,则下列结论正确的是( ).
A.x1<x2<x3B.x2+x3=2
C.f3(x1)<0 D.f3(x2)=f2(x3)
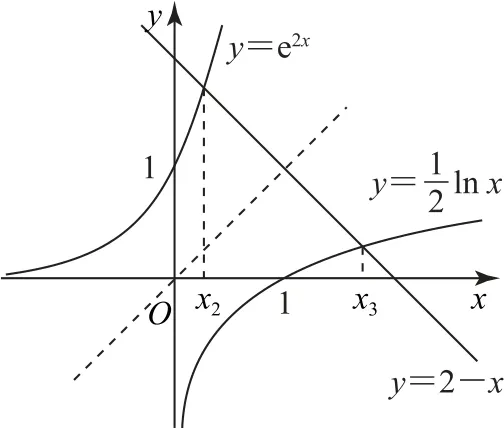
图3
点评本题虽然有二次函数“加盟”,但考查的还是两个互为反函数的指数函数、对数函数同直线y=2-x的交点问题,显然本题的难度在引例的基础上得到了加强.
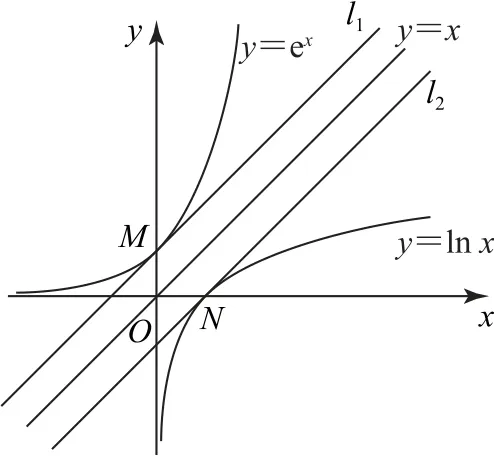
图4
点评解答本题的关键是挖掘
的几何意义,将原问题转化为求y=ex图像上的动点与y=lnx图像上的动点的最小距离,研究的依然是互为反函数的两个函数(指数函数与对数函数)的图像间的关系,所以还是构造与引例相似的图像.
多题一图,变幻无穷.由此可见,当题目中含有两个互为反函数的指数函数与对数函数,且讨论与方程的根或图像交点的问题时,一般可采用数形结合法,都离不开引例解答中的这张图.
(完)
