不同视角破解一道高考“爪子模型”试题
2023-09-10杜海洋
杜海洋
(成都经济技术开发区实验中学校)
2023年数学新高考Ⅱ卷第17题是一道解三角形问题(俗称“爪子模型”),此题题型常规但不乏新意,入口宽、解法多,但不同方法的效果(思维、时间、运算、书写等要求差异较大)相去甚远,故本题也是一道区分度较大的题,而且对后续解题进程会产生较大影响,这突出了高考对“多考想、少考算”“在思维层次上区分”的命题立意.下面笔者对此题进行多视角解答,以飨读者.
1 试题呈现
题目(2023 年新高考Ⅱ卷17)记△ABC的内角A,B,C的对边分别为a,b,c,已知△ABC面积为,D为BC的中点,且AD=1.
(1)若∠ADC=,求tanB;
(2)若b2+c2=8,求b,c.
2 试题分析
本题考查解三角形的基础知识,即正弦定理、余弦定理、面积公式的综合运用,其中中线AD的长度已知,且点D为BC的中点,则BD=DC,这些条件都是求解问题的关键.因为三角形与向量密不可分,所以结合向量进行解答也是解题的一个方向,三角形是几何图形,所以结合几何作图也是这类试题的一个突破口.
3 试题解答
(1)方法1 (利用几何作图)
如图1所示,作AH⊥BC于H,由题设AD=1,∠ADC=,易得
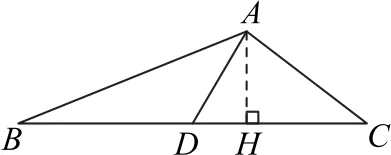
图1
点评在解三角形中,若涉及中点、等分点等特殊情形,可考虑作中位线或平行线进行角与线段的转化,由于题设条件涉及面积,从而作高,构造直角三角形,轻松获得解答.
方法2 (利用面积相等)
点评利用等面积法、余弦定理建立等式关系,得出边a,c的值,再结合正弦定理使问题获解,尤其是“爪子模型”的三角形,利用面积的不同表达形式,可以对三角形涉及的多条线段建立等式关系,这样就可以合理利用已知线段的长度,当然合理利用相邻补角也是解题需关注的一个角度,如sin∠ADB=sin∠ADC,cos∠ADB+cos∠ADC=0.
方法3 (利用面积倍数关系)
因为AD=1,所以DC=2,即BD=2.在△ABD中,
点评此法巧妙运用面积关系求出DC=2,再在△ABD中,根据两边及其所对的两角,利用正弦定理使问题获解,体现了转化与划归的强大逻辑思维能力.
方法4 (几何作图+正弦、余弦定理)
点评本法实质是方法1、方法2的结合,体现了在“考场”上学生解答、思考路径不同,解答题的时间“长度”也不同,但也体现了解答此问目标的一致性,多视角切入,方法的多样性.
方法5 (利用正弦定理+余弦定理)
由①和②可得a=4.下同方法2.
点评求解关于“爪子模型”的三角形,分别利用“大”“小”三角形,结合正弦定理或余弦定理建立边角关系也是常见策略,其中利用“共角”以及两次余弦定理可以建立三角形所涉及线段的关系,进一步获得相关等式.
方法6 (坐标法)
如图2 所示,以点D为坐标原点、BC所在的直线为x轴建立平面直角坐标系,由方法1易得,B(-2,0),所以
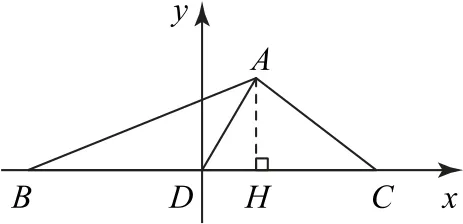
图2
点评坐标法是数形结合的真正体现,坐标法可将复杂的线段或角的关系转化为纯数据处理,从而避免了思维的难度.
(2)方法1 (利用互补关系)
因为在△ABD和△ADC中,由余弦定理可得
点评探究三角形中的线长度与已知三角形三边长度的关系对学生的思维要求较高,基本理念是利用线与边形成的角和余弦定理建立边的关系,其中cos∠ADB+cos∠ADC=0是研究这类问题的核心步骤.
方法2 (利用向量)
点评平面向量具有“数”和“形”的双重性,是沟通几何、代数的重要工具,借助平面向量基本定理建立三角形中边与边之间的等量关系式.此法利用定比分点公式,实质是共线向量基本定理,它体现了三个不共线向量之间的一种数量关系,利用这一关系可将三条线段的长度联系起来,这也正是运用本法的关键所在.
方法3 (坐标法)
如图3所示,以点D为坐标原点、BC所在的直线为x轴建立平面直角坐标系.因为AD=1,设∠ADC=θ∈(0,π),令A(cosθ,sinθ),B(-,0),C(,0),由b2+c2=8,则
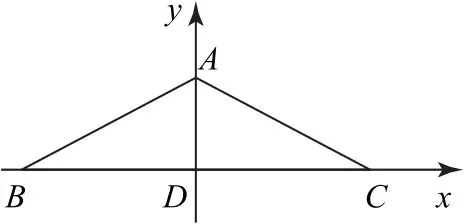
图3
点评通过建立平面直角坐标系,建立等式,探索出AD⊥BC,从而得出AB=AC,再利用勾股定理获得解答.
方法4 (几何作图法)
如图4 所示,延长AD至点H,使AD=DH,连接BH,CH,则易得四边形ABHC为平行四边形,所以AH=2AD=2,BH=b.在△ABH中,有
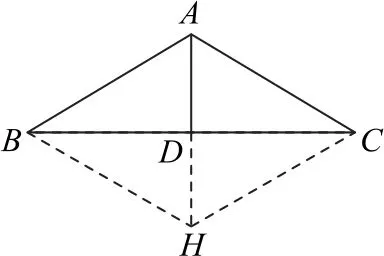
图4
又因为b2+c2=8,所以bccos∠BAC=-2.
下同方法2.
点评此法通过几何作图,将涉及的线段转化到同一个三角形中,根据已知条件,再利用余弦定理和面积公式求得答案.若三角形中涉及边的中线,此几何法高频使用.
方法5 (利用中线长公式)
在△ABC中,由中线长公式可得b2+c2=2(AD2+BD2),则AD2+BD2=4,因为AD=1,所以,下同方法1.
点评中线长定理其实来源于人教A 版《数学必修第二册》第39页例2:如图5所示,已知平行四边形ABCD,你能发现对角线AC和BD的长度与两条邻边AB和AD的长度之间的关系吗?(请读者自行翻阅教材).
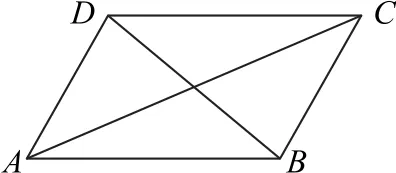
图5
方法6 (利用斯特瓦尔特定理)
斯特瓦尔特定理:如图6 所示,设点D为已知△ABC边BC上的一点,则AB2·DC+AC2·BDAD2·BC=BC·DC·BD.
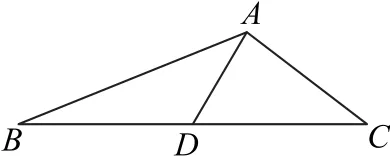
图6
由此定理可得
点评此法巧妙借用了斯特瓦尔特定理,不仅步骤简单,计算量也小,极大提高了解题效率,希望同学们在平时解题中多积累相关的二级结论并加以运用.当然涉及利用斯特瓦尔特定理的试题屡见不鲜,限于篇幅,就不一一赘述,希望读者自行查找相关试题资料.
本文充分展示了涉及三角形中含有线段的问题的几种常规解题思想,尤其要熟练掌握对比解法,优化解题思路.数学家波利亚曾说过:“掌握数学就意味着善于解题”,数学问题的解决仅仅是一个开端,更重要的是解题后的反思与回顾,以便深刻地揭示问题的本质.在解题的过程中,要多角度思考解题思路,深入挖掘问题本质,寻求巧妙的解题方法并及时归纳总结规律和结论,从而提高解题效率.
(完)
