基于PIC-DSMC 算法的嵌套霍尔推进器仿真性能研究

谭 睿，于 博，王平阳

（1.上海交通大学 机械与动力工程学院，上海 200240；2.上海空间推进研究所 电推进事业部，上海 201112）

0 引言

霍尔推进器是一种技术成熟的电推进器，适用于各种各样的太空任务［1-2］。近年来，随着航天技术的进一步发展，对大推力、高比冲的霍尔推力器的需求日益提升［3-4］。然而传统单通道霍尔推进器受到自身几何条件的局限，其尺寸和运行功率受到限制［5］。将推进器进行并联集成，可以利用现有型号的推进器，但是存在尺寸过大且推力密度低的问题［6］。采用嵌套形式的霍尔推进器是合理的解决方案。美国国家航天局（NASA）和格林研究中心（Green Research Center）设计研制的第一个10 kW双流道嵌套霍尔推进器X2 取得了点火成功和相关数据测量［7］。基于嵌套推进器X2 和多个传统霍尔推进器型号的实验数据，研制的三通道嵌套霍尔推进器X3 目前正处于地面实验阶段［8-9］。

嵌套霍尔推进器以传统单通道霍尔推进器为原型，将多个通道嵌套在同一推进器上，嵌套霍尔推进器能够实现大功率运行，以及任何通道之间的组合［10-11］。与此同时，由于地面试验受到成本、设备等因素的制约，最优运行工况往往难以找到，而探索不同的配置和参数，找到最佳运行工况是优化推进器结构的重要手段［12］。数值模拟在很大程度上解决了这个问题，同时也弥补了地面试验成本高、有背压等诸多不利因素，成为推进器可行性验证和设计优化的重要方法［13］。由于目前国内嵌套霍尔推进器还处于初步发展阶段［14］，数值模拟结果对嵌套推进器型号设计和实验平台搭建起到重要的作用。

PIC（Particle-in-Cell）和流体方法是确定所有带电物种空间分布的2 种主要数值方法［15-16］。PIC方法相对于流体方法具有较高的计算精度，因为该模型采用基本方程没有过度简化，跟踪真实的物理过程，包括粒子传输、粒子碰撞和电场计算［17］。静电场和磁场通过求解泊松方程和麦克斯韦方程来计算［18］。本文所采用的几何和磁场结构参考了NASA-457M，NASA-400M 以 及X2 等多种型号［19-20］。仿真羽流场分布结果对于磁场设计改进，几何结构进一步优化和实验设备搭建具有重要的参考意义。

1 PIC-DSMC 算法概述

1.1 PIC 算法

PIC 方法是等离子体物理中粒子模拟的最重要方法之一。国内外也有很多学者采用了有限粒子法对等离子体流动问题进行模拟［21，22］。在PIC 模拟中，通常求解在网格点上进行，网格内的仿真粒子基于特定原则被分配到节点上。一般情况下对平面区域，主要应用面积权重法，而三维时则选择体积权重法。PIC 方法中带电粒子的电荷分配和仿真流程如图1 所示。

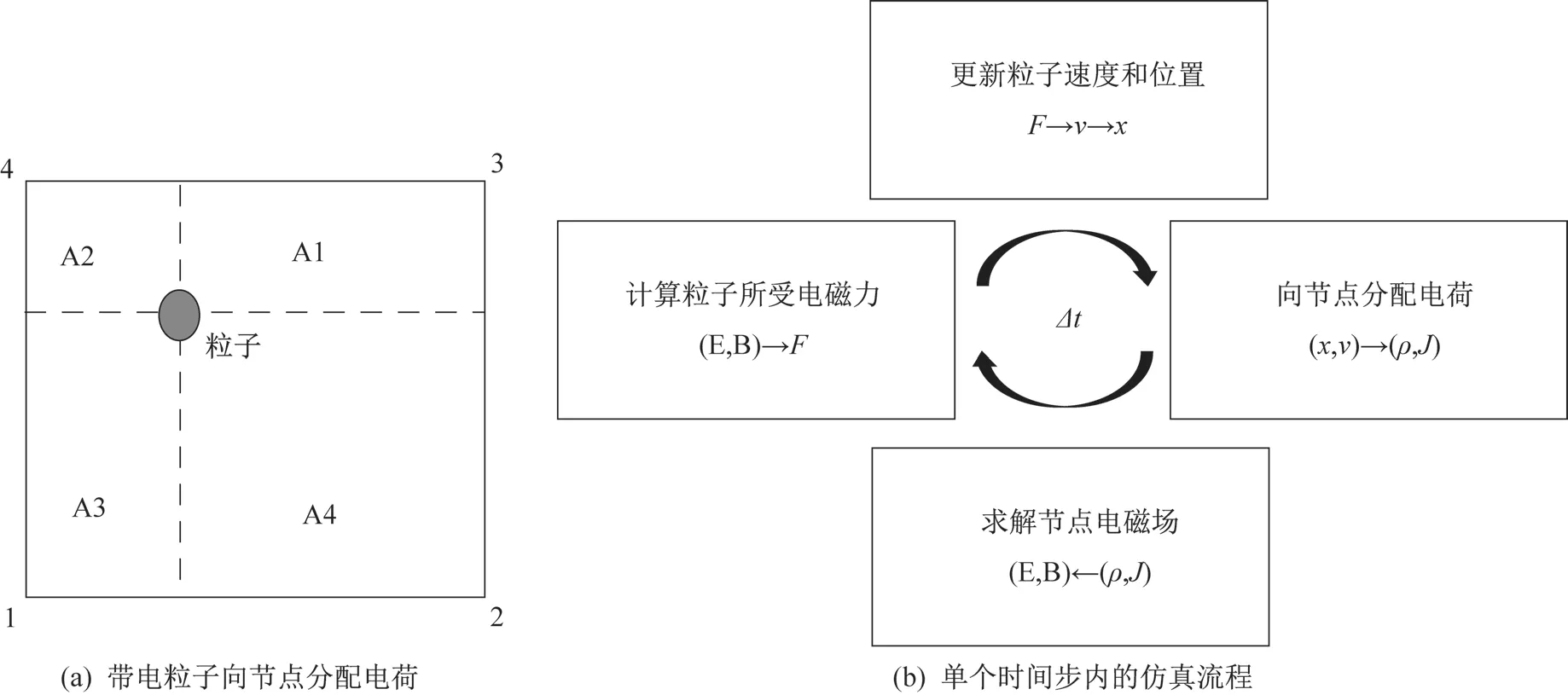
图1 PIC 方法中带电粒子的电荷分配和PIC 算法仿真流程Fig.1 Charge assignment of charged particles to nodes and simulation program of a single time step in the PIC method

电荷分配给网格节点的电量为

式中：qi为第i个节点分配到的电量；q为电荷电量。

通过PIC 算法进行模拟时的流程如图1（b）所示：1）设有大量带电粒子，对其位置和速度参数进行初始化，基于统计平均的方法计算求解域中的电磁场；2）获得每个粒子在该时刻电磁场作用下所受到的电场力和洛伦兹力；3）接着计算出其加速度和速度；4）循环迭代，达到稳定状态后对粒子统计平均输出结果。

1.2 DSMC 算法

DSMC（Direct-Simulation-of-Monte-Carlo-Collision）是为了求解等离子体粒子时间碰撞而引入的算法［23-24］。DSMC 方法是基于如下几方面假设建立的［25］。1）假设在所有计算网格内均发生二元碰撞；2）分子平均间距远大于分子维度，仅在碰撞瞬间考虑分子间作用力；3）碰撞后分子的运动状态只可基于随机抽样方法计算出。

1.3 PIC-DSMC 算法

鉴于电推力器羽流属于超音速稀薄等离子体［26］，其实际流动过程极其复杂。单一的PIC（不考虑粒子间的动量和电荷交换碰撞）或DSMC 法（不考虑电磁场作用）都不能有效模拟其流动问题［27］。20 世纪90 年代，OH 等［28-29］结合上述2 种方法，提出了PIC-DSMC 混合方法，并运用该法对SPT-100、NASA GRC 实验室SPT 等离子体羽流稳态和非稳态进行流动仿真，并取得令人满意的效果。仿真中DSMC 模拟与PIC 模拟相对独立，前者主要用于计算粒子的运动及碰撞，而后者主要用于模拟等离子体自洽电场及其对带电粒子的加速作用，两者涉及的粒子加速、排序、运动等能在一个时间步内同时完成，使得PIC-DSMC 混合法编程过程易于实现。此外，DSMC 仿真在单元进行，而PIC 仿真则在网格点上进行［29］。

PIC-DSMC 算法流程如图2 所示。

2 几何条件和边界条件

嵌套霍尔推进器有内外2 个通道，共有3 种工作模式，推进工质为氙气。与传统单通道霍尔推进器相比，嵌套推进器工作范围更广，推进力更高，能适应未来航天发展多任务化的需求。仿真共采用20 组算例，研究在内外流道采用不同质量流量，以及磁场强度条件下，对推进器羽流流场分布乃至推进器整体推进性能的影响。推进器几何结构如图3 所示。

为了探究在不同工况下嵌套霍尔推进器的推进性能，总共采用20 组工况分别研究内外通道在一系列质量流量与磁场强度下的羽流场特征。质量流量和磁场强度的选择参考了NASA-457M，NASA-400M 以及X2 等多种型号，并通过初步仿真筛选出潜在的最佳工况组合。20 组工况见表1。

表1 自变量为质量流量和磁场强度的最佳工况阵列Tab.1 Optimal working condition array with independent variables of the magnetic field strength and mass flow rate

为提高程序计算效率，如图4 所示，对求解域进行划分而得到7 个子区域，其中各子区域的网格长度为等比级数，各网格含4 个子网格，进行划分后总共获得336 00 个矩形计算网格。计算网格的最小尺度为0.1 mm×0.1 mm，而嵌套霍尔推进器羽流出口处的碰撞的平均自由程约为1 m，德拜长度约为5×10-5m［12］，因此模型基本满足等离子体二元碰撞假设。粒子运动时间步长取10-8s，满足等离子体频率限制和碰撞过程仿真要求。在流场达到稳态后，取100 次抽样均值当做为一组结果，共输出50次，最后再取均值。仿真中总共使用了240 000 个仿真粒子（不包含背压粒子）。

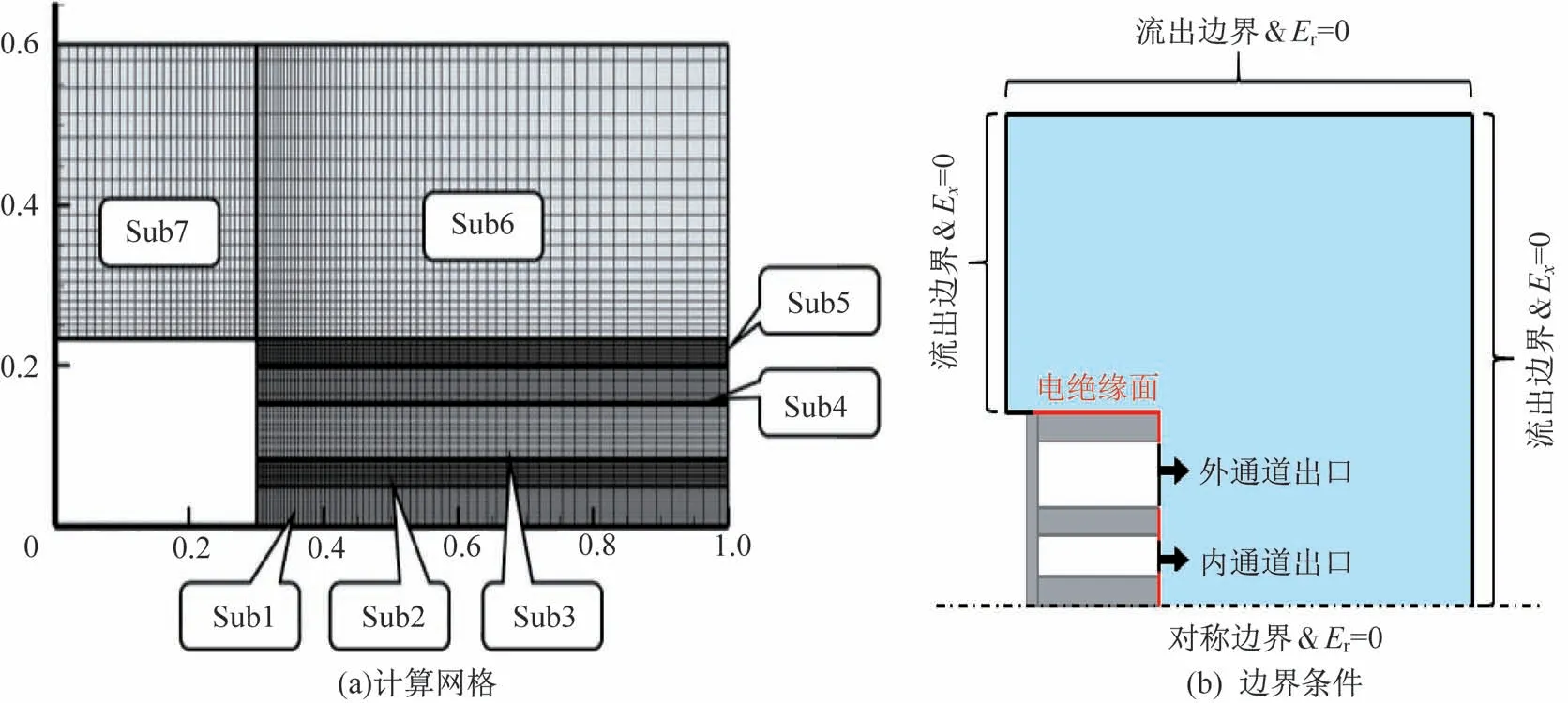
图4 计算网格与边界条件Fig.4 Computational grid and boundary conditions

本次仿真过程中，内通道内外半径分别为51.5、84.5 mm；外通道内外半径分别为151.1、198.5 mm。模拟区域采用二维旋转对称模型，旋转对称轴虚线表示如图4（b）所示，对称轴处采用反射边界条件，径向电场强度等于0；固体壁面均采用反射边界条件，电势取0；计算区域长度取1 000 mm，计算区域半径取600 mm，边界面均认为是与真空交界面，采用出流边界条件，且出垂直于边界面的电场强度取0。回流区域长度取300 mm。

3 仿真结果及分析

3.1 羽流场结果云图

本次模拟结果所展示云图均为Case1 工况条件下结果云图，如图5 所示，图5 中，横轴表示沿着推力器轴线方向的距离，m；纵轴表示距离推力器中心的距离，m。

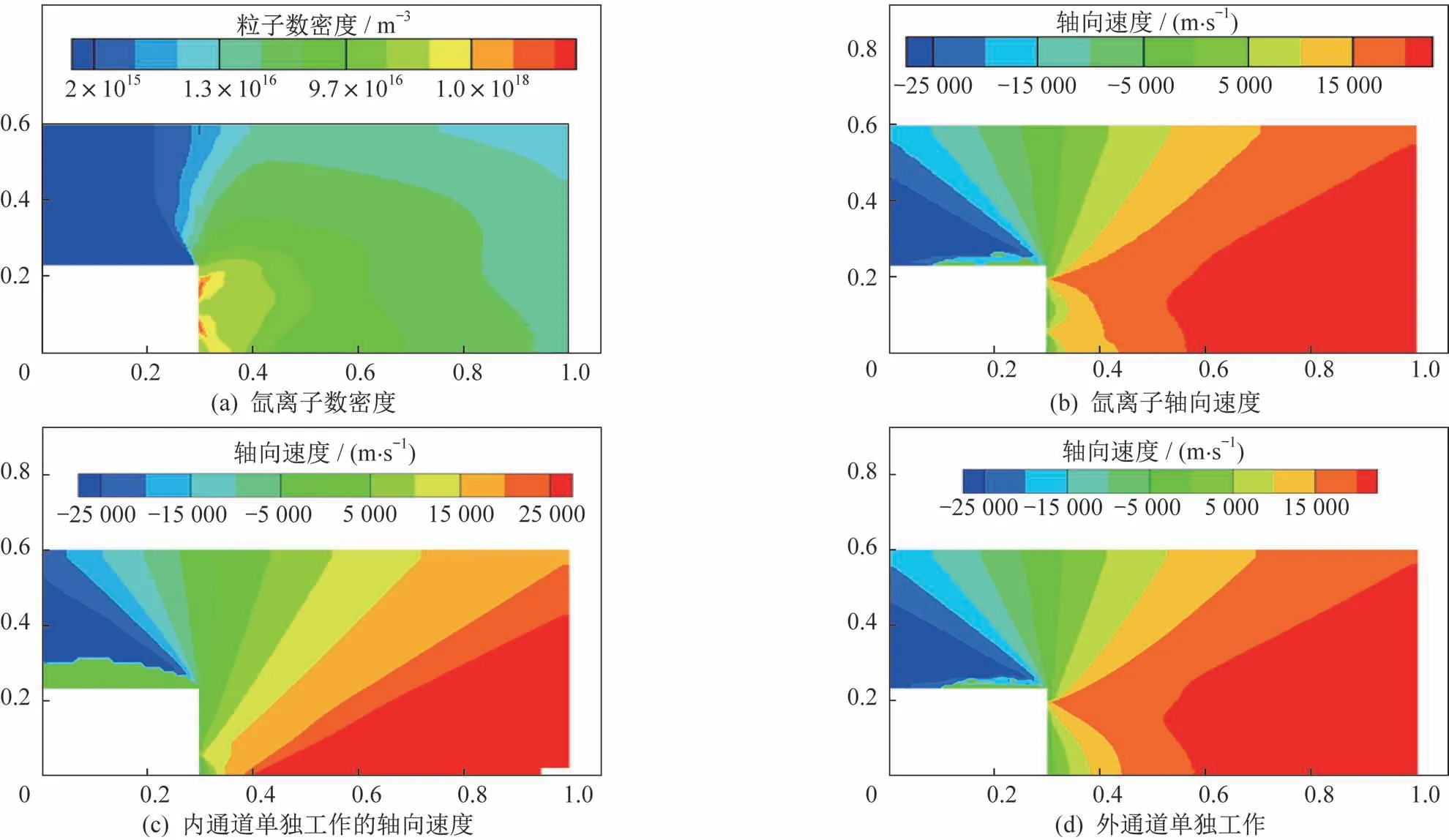
图5 Case1 工况条件下结果云图（长度单位：m）Fig.5 Result contours under Case1 working condition（m）

3.2 羽流发散角

嵌套霍尔推进器羽流发散半角为25°～33°。从发散角总体变化趋势来看。随着推进器质量流量减小，推进器羽流发散角会减小。在保持质量流量恒定时，内通道磁场强度适当增大有利于羽流发散角减小，外流道磁场强度增大则会导致羽流发散角增大。因此，一定范围内提高内通道的质量流量和磁场强度有利于约束羽流发散角，提高推进效率，从而改善推进器整体性能。羽流发散角随质量流量和最大磁场强度的变化如图6 所示。

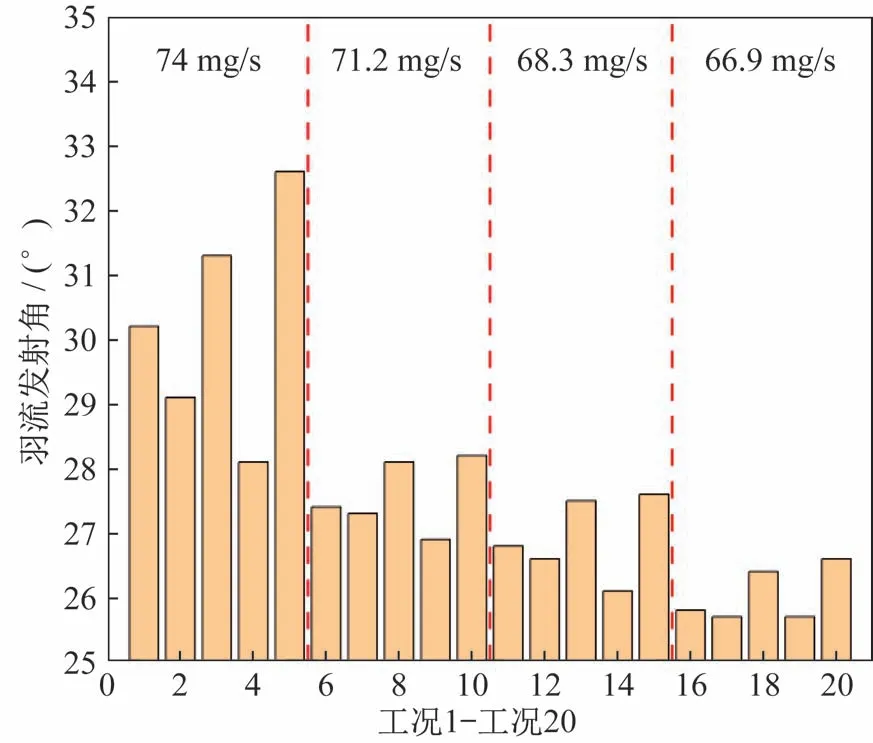
图6 不同工况下的羽流发散角Fig.6 Plume divergence angles under different working conditions

3.3 推力和比冲

推进力和比冲受质量流量、磁场强度的影响见表2。

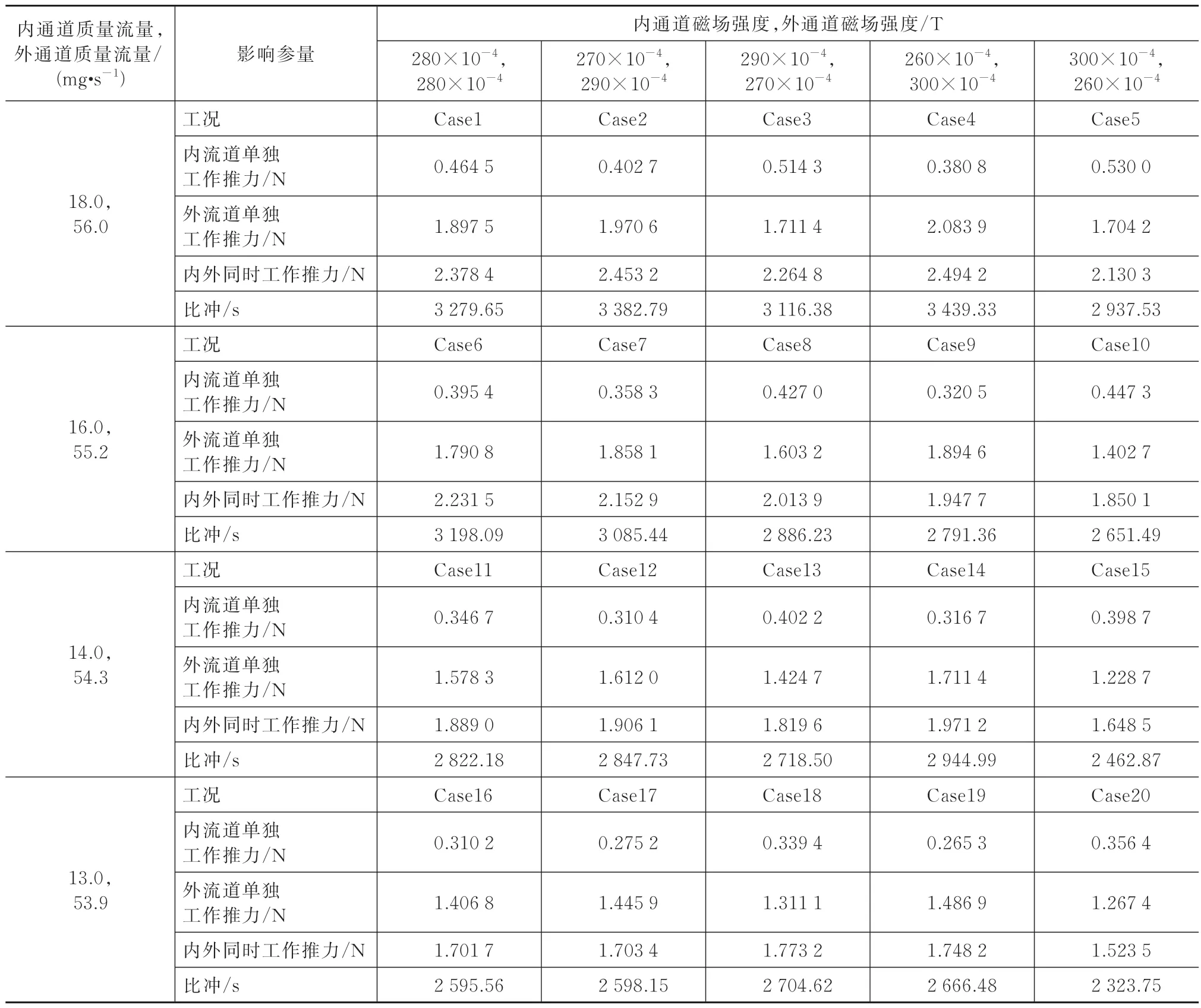
表2 推进力和比冲受质量流量、磁场强度的影响Tab.2 Effects of the mass flow and magnetic field strength on the propulsion and specific impulse

在相同磁场强度下，推进力与质量流率成正相关。在相同质量流量下，推进力与磁场强度成正相关。推进力大小为1.5～2.5 N，比冲为2 300～3 200 s。

4 结束语

推进力、比冲和羽流发散角是衡量推进器推进性能的重要物理参数。推进力可以衡量推进器在短时间内的最大工作负荷。比冲和羽流发散角可以衡量推进工质利用效率。本次数值模拟针对嵌套霍尔推进器羽流进行数值仿真，得到双通道质量流率和最大磁场强度对推进性能的影响。

本次模拟推进力大小为1.5～2.5 N，与磁场强度和质量流率成正相关。推进器比冲为2 300～3 200 s，与质量流量和磁场强度成正相关。质量流率越大，经过电离而产生的正价粒子也越多，推进力越大。同时，在特定条件下找到合适的最大磁场强度能够实现推进器的高效率运行。

本次模拟半羽流发散半角为25°～33°。嵌套霍尔推进器羽流发散角高于一般单通道霍尔推进器，这是由嵌套霍尔推进器特殊的几何结构所决定的。随着质量流率的减小，羽流发散角也会随之减小。在保持质量流量恒定时，内通道磁场适当增大有利于羽流发散角减小，外通道磁场强度增大则会导致羽流发散角增大。因此在设计嵌套霍尔推进器时，一定范围内提高内通道的质量流量和磁场强度有利于提升推进效率，改善推进性能。

基于此次仿真结果，后续将进一步增大内通道质量流量和磁场强度进行羽流仿真，从而达到进一步约束羽流发散角的目的。同时，在该型号嵌套霍尔推进器完成点火实验并进行性能评估后，会进一步与本次仿真结果和国外X2 等现有型号进行性能对比，从而对推力器结构进行进一步的优化。