格栅尾翼布局的姿轨控直接力气动力特性研究

2023-09-06李小林吴王浩周波华

上海航天 2023年4期

李小林，吴王浩，周波华，梁伟，杨帆

（1.上海机电工程研究所，上海 201109；2.上海航天技术研究院，上海 201109）

0 引言

随着科技技术的不断发展，世界各国在空袭作战中不断应用各种高新技术，作战手段日趋多样化，导弹的飞行速度、隐身性能、突防能力不断提高。以可机动变轨［1］战术弹道导弹和临近空间高超声速打击武器为代表的高突防能力目标，对现有的防空反导体系带来巨大威胁。

常规的面空导弹依靠空气舵进行控制，在一定高度范围内能够满足过载要求。但在反导反临作战20～40 km 高度内，空气舵舵效随着飞行高度的增加而显著降低，且由于高空时导弹动压低，弹体升力产生的过载不足，对于高速大机动目标很难直接命中。因此使用直接力控制［2］是提高面空导弹末端机动能力和制导精度的有效方法。

目前国外具备大气层内弹道导弹拦截能力的典型导弹有美国THAAD 拦截弹、PAC-3 系统的Erint拦截弹、俄罗斯S-400 系统的9M96E2 拦截弹以及欧洲的Aster-30 防空导弹。以上典型拦截弹均带有直接力控制系统，根据直接力的作用位置不同，直接力控制分为姿控和轨控［3］两种。PAC-3 导弹在前端安装有180 个小型直接力喷管，通过不同喷口组合喷流提高导弹姿态响应速度。轨控式直接力控制的喷口一般安装在导弹质心附近，9M96E2 导弹和Aster-30 导弹均采用轨控式控制。THAAD 导弹的主级则采用姿轨控组合控制。直气复合控制技术目前已经成为防空导弹系统的核心技术之一，姿轨控喷流气动干扰问题也是近年来的研究热点之一。

国外从20 世纪开始研究直接力控制和喷流干扰机理［8-11］，对喷流参数设置以及喷流对流场的影响有了较为全面的认识［26］。国内通过实验和数值模拟的方法对喷流控制进行了研究［12-15］，提出了一些适用于工程应用的插值方法。

格栅翼［4］是一种非常规翼面，其结构是由外部框架和内部格栅构成的空间多升力部件。苏联于20 世纪60 年代将格栅翼应用于联盟号宇宙飞船救生逃逸系统的稳定、减速部件［5］。美国在“猎户座”逃逸飞行器中也使用了格栅翼。格栅翼首次作为操纵面在战术导弹中应用的成功案例是俄罗斯的R-77 空空导弹［6］。2002 年，德国试飞了带格栅翼的高超声速导弹。我国也于20 世纪90 年代将格栅翼应用于“长征”系列火箭。

格栅翼的优点主要有：1）不易失速，升力特性好；2）作为舵面使用时铰链力矩小；3）格栅翼可以折叠紧贴弹体安装，折叠后弹体包络小。格栅翼的主要缺点是阻力大，且格栅翼在跨声速段有堵塞特性，会改变弹体的气动特性。

国外从对格栅翼进行了大量的研究［16-19］，包括影响栅格翼气动性能的各种因素，如马赫数、高度、前后掠角等；国内针对格栅翼也进行了相关研究［20-22］，如曲面格栅翼和后掠角等，同时还针对格栅翼风洞试验时难以缩比提出了相关的解决方案。

在末端使用格栅尾翼可以充分发挥格栅翼的优势，并基本不受其缺点的影响：首先，格栅翼使主级压心后移，保证主级与助推分离安全；其次，格栅翼只在拦截末端展开，不影响导弹射程；再次，格栅翼展开时主级的飞行马赫数较高，堵塞特性不明显，能够充分发挥格栅的效果；最后，格栅翼可以折叠贴在主级上，不影响全弹的压心。

目前国内外尚未研究过格栅翼与姿轨控组合喷流的新型布局，特别是姿轨控直接力工作时对格栅翼气动特性的影响特性和机理不清楚，因此需要开展此研究，充分发挥姿轨控直接力和格栅翼气动的优点。本文采用计算流体力学（Computational Fluid Dynamics，CFD）方法，通过与试验结果对比来校正计算模型，从而得到置信度较高的结果。

本文提出了一种采用格栅尾翼和姿轨控直接力复合控制的末级导弹布局。该布局主要优点是依靠格栅尾翼调整全弹的压心，弹身不需要设计较大的锥角，增大了导弹内部的空间，且在全弹飞行时格栅翼处于折叠状态，在弹道末端展开，有效地减小了飞行阻力。

1 格栅翼布局CFD 计算方法研究

使用CFD 方法研究格栅翼问题前需要预先开展有效性验证［7］。采用N-S（Navier-Stokes）方程来研究此类问题已为业内普遍接受［22-23］。在新型气动布局研究之前需要分别对格栅翼和喷流开展计算方法有效性验证。首先选取文献［24］中的某格栅标模模型作为验证计算方法的参照对象，文献［24］中栅舵尺寸如图2 所示。

选取三维可压雷诺平均的N-S 方程（Reynolds Averaged Navier-Stokes Equation，RANS）作为主控方程，RANS 方程表达式为

式中：U为解向量；F和G为通量向量。

式中：ρ、p、e、T、k分别为密度、压强、能量、温度、热传导系数；ui为沿直角坐标系xi方向的速度分量；i、m为整数，取1～3，分别对应直角坐标系的3 个方向。Ma∞为来流马赫数；γ为比热比；Re∞为来流的雷诺数。

黏性切应力的分量为

式中：δmi为Kronecker 符号；j为整数，取1～3。

黏性系数之间的关系为

式中：μL为层流黏性系数；μT为湍流黏性系数。

式中：PrL、PrT分别为层流普朗特数和湍流普朗特数。

湍流模型选取目前对逆压梯度适应性好、计算量较小、稳定性较好的S-A（Spalart-Allmaras）一方程湍流模型［25］，采用二阶精度的离散格式。

采用非结构网格，圆柱形外场，外场半径取5 倍弹长，由外场向模型网格逐渐加密，边界条件设置为压力远场。力矩系数参考点为外形前缘顶点，参考面积和长度，分别取模型弹径和弹长。设置模型物面外共生成15 层边界层网格，第1 层网格厚度取0.05 mm。格栅翼和弹体网格如图3 所示。

格栅翼标模的单片舵面的法向力系数CN的CFD 计算值与试验值的对比结果如图4 所示。图4（a）和图4（b）分别对应Ma=2.5 和Ma=3.5 的状态，从对比结果来看，计算数值与试验数值吻合较好，CN最大误差不超过5%。使用的CFD 计算方法有效，计算结果可信。

2 直接力气动力复合的CFD 计算方法研究

选取文献［11］中的模型即CCF（Cone-Cylinder-Flare）导弹模型，作为验证喷流计算方法的参照对象。该模型由圆锥段、圆柱段和扩张裙尾段组成，其中圆锥段长度为112 mm，直径为40 mm；圆柱段长度为128 mm，直径与圆锥段一致；裙尾段长为120 mm，前后端直径分别为40 mm 和66.4 mm。侧喷口处于圆柱段中间位置，距离头部尖点168 mm，直径为4 mm。CCF 导弹喷流试验结果在ISL（French-German Institute of Saint-Louis）的亚跨超风洞中获得。

建立结构网格，使用半模进行计算，网格总数约为500 万，第1 层网格高度为0.005 mm。流场物面、对称面网格以及喷口网格细节如图5 所示。

计算状态选择Ma=3.0，攻角α=0°，来流采用远场边界条件，来流静压P∞=19 500 Pa，静温T∞=103.2 K。物面采用无滑移边界条件，喷口采用总温、总压边界条件，喷口总压P0=975 000 Pa，总温T0=267.6 K。为了比较不同湍流模型对喷流计算结果的影响，本文分别使用了多个湍流模型进行计算。导弹上表面对称线的压力系数分布计算结果与试验结果的对比情况如图6 所示。

采用二阶精度计算，3 种湍流模型喷流计算结果与试验结果一致性良好。喷口附近位置三者压力系数略有差别，K-ε 模型计算结果较S-A 和SST偏高。总的来说，S-A 与SST 湍流模型结果与试验值一致性更好。说明使用的CFD 计算方法有效，完成了N-S 方程计算方法验证。

3 格栅翼导弹喷流干扰数值模拟

格栅翼导弹外形如图7 所示，计算模型为半模，采用圆锥形头部，头部直径为300 mm，头部长度675 mm，弹身底部直径340 mm，全弹长度1 800 mm，在距离头部顶点1 040 mm 处，布置3 个轨控喷口，分别标记为GK1～GK3，在距离头部顶点1 765 mm 处，布置2 个姿控喷口，分别标记为ZK1～ZK2，如图8 所示。为了研究喷流对各部件气动力的影响，在后续图表中命名弹身（不含导弹底面）为body，顺航向看，左上方格栅翼面为wing1，左下方格栅翼面为wing2，外形全弹气动力记为Net。

格栅翼导弹网格如图9 所示，在两片格栅翼四周流场区域采用非结构网格，其他流场空间均采用结构网格。边界层第1 层厚度设置为0.1 mm。计算状态选择Ma=6.0，攻角α=0°、5°、10°，以模拟末端导弹主级飞行条件，来流采用远场边界条件，选取20 km 的标准大气参数作为参考，来流静压P∞=5 529.3 Pa，静温T∞=216.65 K。物面采用无滑移边界条件，喷口采用总温、总压边界条件，从喉道开始计算，轨控喷口总压P0=83 71 56 1 Pa，总温T0=260 K；姿控喷口总压P0=4 703 778 Pa，总温T0=260 K。根据第2 节的分析结果，选取S-A 湍流模型，计算精度二阶，为便于对比分析，对图中不同喷流组合进行了命名见表1。

表1 喷流组合命名列表Tab.1 Names of different jet combinations

在图8 中，Z=-0.22 m 处做流场切片，该切片位置有无轨控喷流、不同攻角的马赫数云图如图10所示。图10 中从左往右依次为无喷0°、5°和10°攻角、从上往下依次为无喷和有喷（轨控2 号喷口）的流场。

图1 拦截弹分离作战Fig.1 Schematic diagram of missile separation

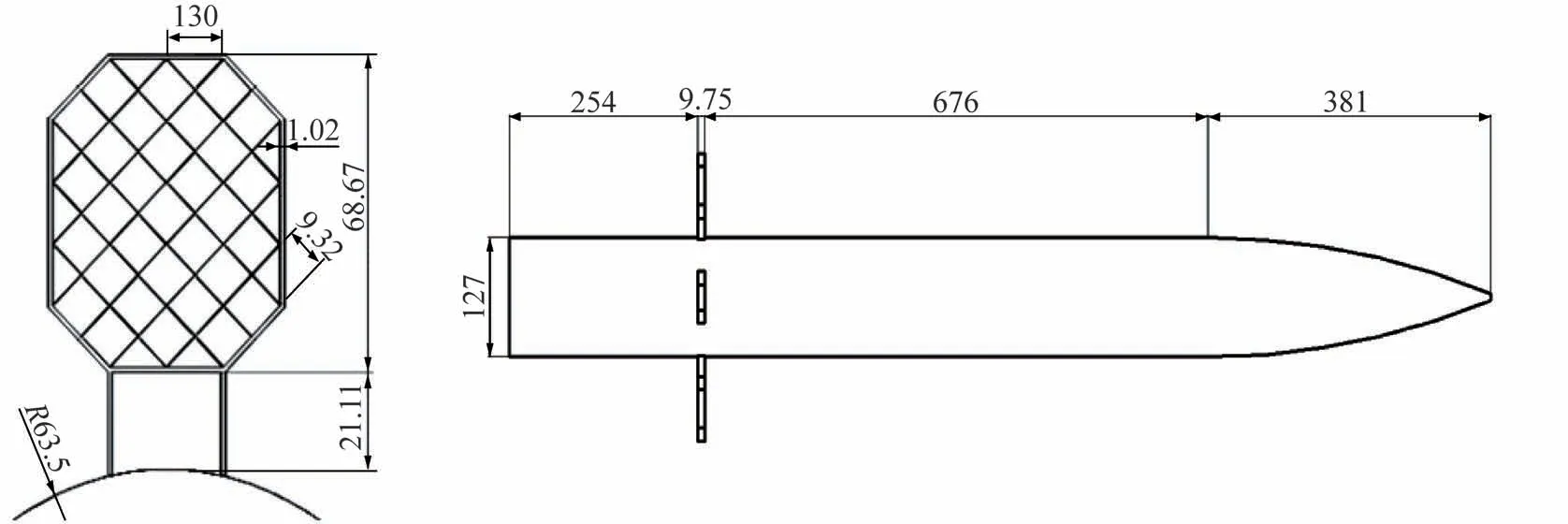
图2 标模尺寸Fig.2 Size of the standard model

图3 格栅翼与弹体网格Fig.3 Meshes of the grid fin and missile body

图4 法向力系数对比Fig.4 Comparison of the normal force coefficient

图5 CCF 模型结构网格Fig.5 Structure meshes of the CCF model

图6 压力系数分布Fig.6 Distribution of the pressure coefficient

图7 格栅翼导弹外形Fig.7 Profile of the missile with grid fin

图8 喷口位置Fig.8 Schematic diagram of the jet positions

图9 格栅翼导弹网格Fig.9 Meshes of the missile with grid fin

图10 切片马赫数云图（Z=-0.22 m）Fig.10 Slice contours of the mach number（Z=-0.22 m）

流场表明无喷时格栅翼的内部都没有出现激波反射，说明在该工况下使用格栅翼不会出现壅塞现象。格栅翼的外框厚度相比格栅要大，邻居外框的格子通流性能较差，在外形优化时可以考虑对外框做修型优化。

当2 号轨控喷口开启后，喷口正后方首先是形成椭圆形的高速流场，之后流动速度降低，形成类似钟表指针的流动结构，随着攻角的增加，格栅1 会受到喷流影响，而格栅2 基本不受影响，两片格栅的流动差异会随着攻角的增大而增大，产生的纵向、横向扰动均需要姿控控制力克服。因此布局不宜在大攻角时使用。

各喷口组合状态半模模型的前体轴向力对比结果如图11 所示。图11（b）～图11（d）给出了0°、5°、10°这3 个攻角时，单独喷口喷流各部件的前体轴向力分布曲线。轨控喷流导致前体轴向力减小，姿控喷流基本不影响前体轴向力。部件气动力分析表明，轨控导致格栅翼的前体轴向力减小。

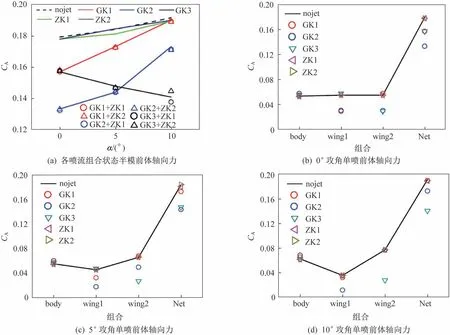
图11 前体轴向力系数Fig.11 Results of the axial force coefficient of the forebody

喷流干扰流场在X-Z平面以及X=-1.2 m、X=-1.4 m 和X=-1.6 m 这3 个站位的压力系数云图如图12 所示，从图12 中可以观察到轨控喷流后方产生的大片低压甚至负压区域，是导致前体轴向力减小的根本原因。

图12 压力系数云图Fig.12 Contours of the pressure coefficient

各喷流状态全弹法向力对比曲线如图13 所示。图13（b）～图13（d）给出了0°、5°、10°这3 个攻角时，单独喷口喷流各部件的法向力分布曲线。姿控喷流对全弹法向力系数影响较小，轨控喷流主要影响弹体法向力从而影响全弹法向力。组合喷流的法向力曲线与纯轨控喷流的法向力曲线基本平行，说明对于法向力，姿控与轨控喷流的耦合效应不明显。

图13 法向力系数Fig.13 Results of the normal force coefficient

各喷流状态全弹俯仰力矩（相对头部）、全弹滚转力矩对比曲线如图14 所示，组合喷流对俯仰力矩、滚转力矩的影响结论与法向力类似。

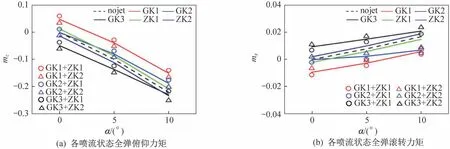
图14 俯仰力矩与滚转力矩Fig.14 Results of the pitch moment and roll moment

5°、10°攻角各单独喷流状态的全弹压心如图15所示，相比无喷状态，除2 号迎风面姿控喷口喷流时，全弹压心后移，其他喷口喷流时，全弹压心均往前移，最大前移出现在5°攻角，2 号轨控喷口喷流时，前移量达到5%。由于轨控喷口总压大，轨控喷口开启后全弹弹体中部形成的高压区导致了压心前移。

图15 喷流组合状态压心Fig.15 Pressure center of different jet combinations

各喷流组合状态相对无喷状态的法向力、俯仰力矩以及滚转力矩差量和组合喷流相对单喷口喷流的差量见表2、表3。

表2 喷流组合列表1Tab.2 List 1：jet combinations

表3 喷流组合列表2Tab.3 List 2：jet combinations

在各个攻角下，GK1+ZK1 组合喷流的法向力与GK1 的法向力的差量约等于ZK1 与无喷的法向力差量，且该差量基本不随攻角变化，分析其他姿轨控组合喷流可以得到相同的规律。证明了姿轨控是可以解耦的。从表2 和表3 可以看出，单独轨控相对无喷的差量随攻角和迎背风状态而改变，而单独姿控相对无喷的差量基本不随攻角改变，迎背风的干扰量大小基本相等，符号相反，说明姿控干扰量可以作为一个固定的恒值扰动，从而大幅简化喷流干扰的气动力数学建模。