基于载波平滑伪码的高精度航天扩频体制测距技术

张国亭，刘保国，王 宏，徐茂格，董光亮

（1.国防科技大学 空天科学学院，湖南 长沙 410073；2.北京跟踪与通信技术研究所，北京 100094；3.中国西南电子技术研究所，四川 成都 610036）

0 引言

航天器轨道测量与确定是测控系统的核心能力之一，也是保证航天器正常运行和应用效能充分有效的重要基础［1-2］。近年来，随着光学卫星、微波探测卫星、合成孔径雷达（Synthetic Aperture Radar，SAR）成像卫星型号的成功部署和载荷能力的快速提升，该类卫星的应用需求越来越广泛，测控任务需求激增［3-4］，同时对轨道测量与定位精度要求也进一步提升，米级至十米级的定轨精度需求日益凸显，高精度测定轨关键技术成为研究热点［5-7］。目前，国际上通常采用多站测距系统进行高轨卫星高精度测定轨，其中关键要素之一是如何突破高精度距离测量，减小距离测量误差，提高测定轨精度［8-10］。测量误差主要包括随机误差和系统误差［11］，其中随机误差指不可预测的偏差，航天器测距随机误差通常相关性小，且由于相对运动随时变化，无法用解析函数来参数化描述，必须通过概率分析与统计理论来归纳研究［12-13］。引起测距随机误差的主要因素包括热噪声、电磁环境干扰、机械测不准等，为了提高测距精度，在信道电平一定的情况下，一般采用压缩测距环路带宽的方式来实现［14-15］。但是，测量环路带宽太窄会增大信号捕获的时间，同时增加信号跟踪的难度，这主要是由于过窄的环路带宽会引入跟踪动态滞后误差，轻则表现为增加测距的系统误差，重则使环路失锁［16-18］。

基于非相干测量体制的星地测距中，采用载波辅助跟踪可有效缩短捕获时间和减少动态跟踪滞后量［19-20］。载波和伪码是对同一目标运动进行观测，载波锁定时两者的距离增量相同，载波频率高，其相位测量的随机误差小［21］，因此，可利用载波相位测量结果对伪码值进行平滑，降低伪码测量的随机误差［22］。本文提出了一种基于载波平滑伪码的高精度航天扩频体制测距技术，其主要原理为利用载波相位测量精度高于伪码跟踪精度的特性，通过锁相环跟踪得到的载波相位，并对伪码跟踪环路相位进行平滑，在保留伪码测量无相位模糊特性的基础上进一步提升测量精度，以减小测距接收机的测距随机误差。

1 载波平滑伪码高精度测距技术

采用非相干测量体制进行星地测距，在第k次观测时，伪码相位观测方程和载波相位的观测方程分别可以表示为

式中：ρk、ϕk分别为k时刻的伪距和载波相位观测值；rk为k时刻的真实星地距离；c为光速；δtu，k分别为k时刻的接收机钟差和卫星钟差；Ik、Tk分别为k时刻的电离层延迟和对流层延迟；λ为载波波长；N为载波相位模糊用整周模糊度；ερ，k、εϕ，k分别为伪码相位和载波相位的测量噪声。

如果测距接收机持续锁定载波，未产生失周现象，则式（2）中的整周模糊度N为固定值。为了消除周期模糊度，可以对两个连续时刻的伪码相位观测值和载波相位观测值作差分，得到

其中，差分量Δρk和Δϕk的定义分别为

对比式（3）和式（4）可以发现：伪码变化量Δρk的表达式、载波相位变化量与波长的乘积λ⋅Δϕk表达式非常相似。当电离层延时变化量ΔIk较小，可以被忽略时，则除了误差项Δρk和λ⋅Δϕk，两者在数值上差异不大。由于伪码变化量Δρk、载波相位变化量与波长的乘积λ⋅Δϕk在理论上相等，两者相结合即可得到平滑且无模糊度的距离测量值。

利用载波相位测量结果对伪码相位进行平滑处理［23］，表示为

式中：ρs，k为k时刻的载波相位平滑伪码测量结果；M为平滑时间常数，表示载波相位对平滑结果的影响程度；ρk为k时刻的伪码观测值；ϕk为k时刻的载波相位观测值；λ为载波波长。

对于下行链路，下行载波相位平滑下行伪码相位测量结果的计算公式为

对于上行链路，上行载波相位平滑上行伪码相位测量结果的计算公式为

2 仿真试验结果

2.1 载波平滑伪码测距算法仿真

式（7）是一种常用的平滑公式，利用载波相位测量值来对距离测量值进行平滑处理，从而均衡部分测量误差。其中，平滑时间常数M一般为接收机的默认参数，介于20～100 个历元（s），该值也可以由用户自行设置或者通过调试确定［24］。M值越大，平滑结果ρs，k就越依赖于载波相位观测量，平滑效果也越明显。下面通过数值仿真来呈现M值对平滑结果的影响。M取30 时载波相位平滑前后测距的随机误差分布如图1 所示，可以直观地发现载波平滑后效果明显，测距结果更加精确平滑。

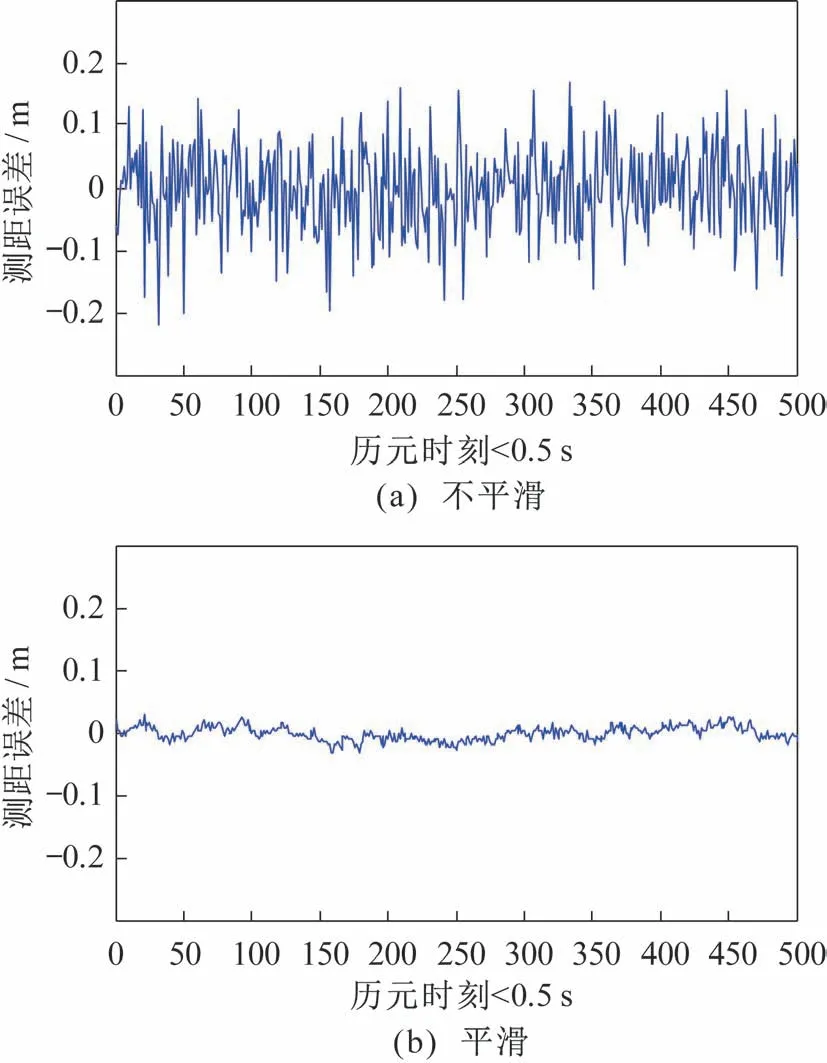
图1 载波平滑前后测距结果对比Fig.1 Comparison of the ranging results before and after carrier smoothing

该方法对接收机的锁相性能有一定的要求，一旦载波相位失锁，可能导致整周模糊度产生跳变，N不再为固定值，这就需要重新设置平滑参数才能维持平滑效果。接收机通常将持续锁相后的第一个伪距观测值ρ1作为ρs，1的初始值，即

式（10）中，如果平滑伪距初始值ρs，1与真值偏差较大，那么平滑器需要迭代多个采样周期才能均衡此偏差［25］。因此，初始值ρs，1的选取应尽可能接近真值。为了获取一个相对准确的初始值，在平滑处理之前，可用以下公式先尽量多估算几个ρs，1的初始值，然后再将其平均值作为初始值，即：

仿真环境搭建：假定伪码测距跟踪误差为3 m（1σ），载波相位跟踪误差为0.002 m（1σ），假设电离层延时保持不变，平滑时间常数为100。仿真结果如图2 所示。

图2 单频载波相位平滑算法测距结果Fig.2 Ranging results of the single-frequency carrier phase smoothing algorithm

2.2 平滑时间常数对算法收敛效果影响仿真

在平滑算法中，设置不同的时间常数对最终的测距值误差影响较大。一般情况下，时间常数越大，算法收敛过程越长，如图3 所示，接收机需要较长的时间进行测距值收敛。因此，在高动态的应用环境中，建议采用小的平滑时间常数。但是，平滑时间常数不能过小，该常数会直接影响接收机测距值随机误差的大小。如图4 所示，接收机测距收敛后，进入稳定的跟踪阶段，时间常数设置越大，结果的随机误差越小。

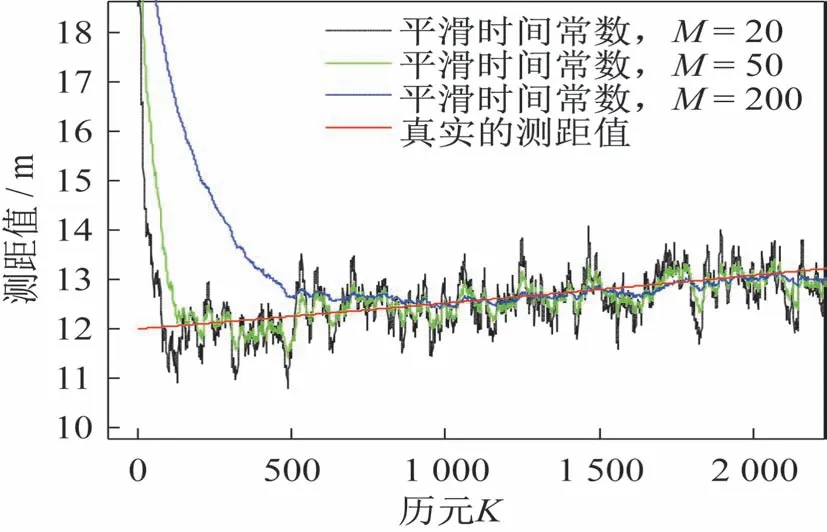
图3 载波相位平滑伪码测距值初始段（收敛过程）Fig.3 Ranging values during the initial segment with the carrier phase smoothed pseudo-code（convergence procedure）

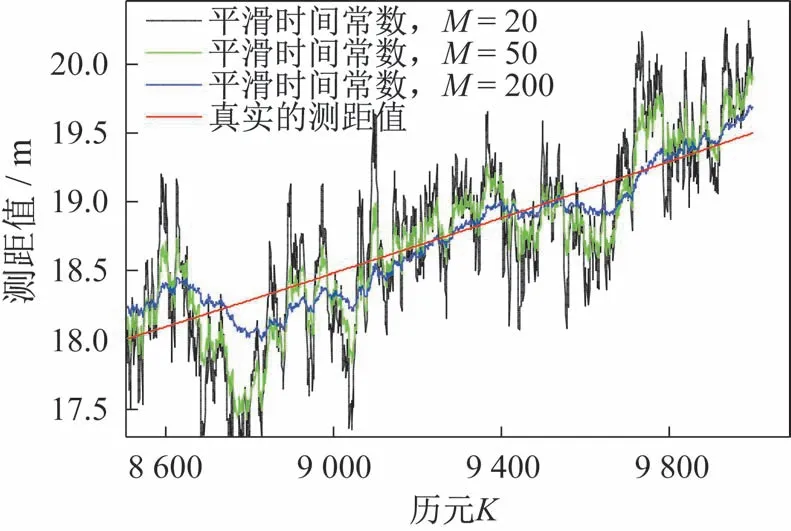
图4 载波相位平滑伪码测距值跟踪段（稳态）Fig.4 Ranging values during the tracking segment with the carrier phase smoothed pseudo-code（steady state）

由图4 可知，伪码相位测距的误差（1σ）大概为3 m，载波相位测量值的误差（1σ）大概为0.002 m，采用载波相位平滑算法后的测距值误差（1σ）分别为0.492 9 m（时间常数为20），0.308 4 m（时间常数为50）和0.182 6 m（时间常数为200）。仿真结果表明，载波相位平滑伪码测距算法可以使测距值的误差减小一个数量级。

3 外场试验结果

利用星、地高精度测距试验样机，对某频段基于载波相位测量的高精度测距技术的性能开展试验验证，其连接如图5 所示。主要试验参数为码环带宽（双边）：1.2 Hz；载波环路带宽（双边）：200 Hz。实验结果见表1 和表2，其中，表1 为没有使用载波相位测量功能时的测距随机误差结果，表2 为使用载波相位测量功能时的测距随机误差结果，根据对比可以发现采用基于载波相位测量的高精度测距技术后，测距随机误差有明显降低，验证了该技术的可行性。

表1 测距随机误差测试结果（未使用载波相位测量功能）Tab.1 Test results of the ranging random error（without carrier phase smoothing）

表2 测距随机误差测试结果（使用载波相位测量功能）Tab.2 Test results of the ranging random error（with carrier phase smoothing）

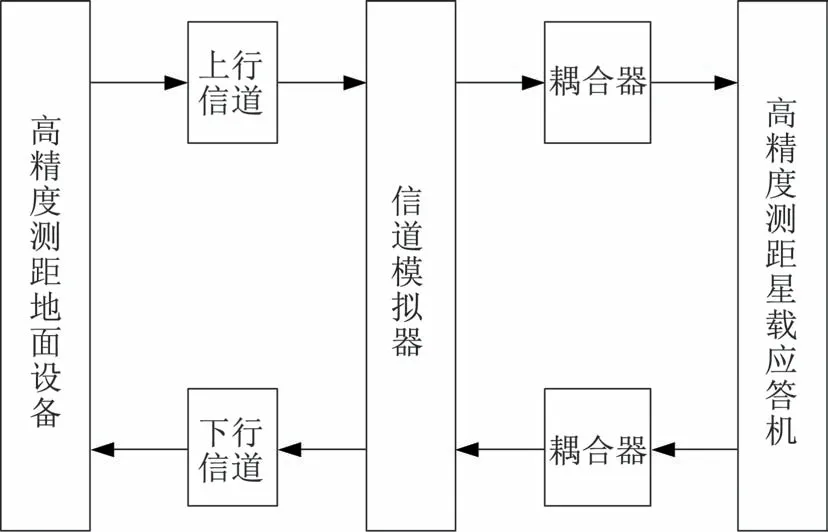
图5 高精度测距样机测试连接Fig.5 Test connection diagram of the high-precision ranging prototype

4 结束语

本文提出了一种基于载波平滑伪码的高精度航天扩频体制测距技术，根据载波相位测量精度高于伪码跟踪精度的特性，利用接收机锁相环得到的载波相位对双向伪码跟踪环路进行平滑处理，在保留伪码测量无相位模糊特性的基础上可进一步提升测量精度。对于上行链路，接收机利用下行测量帧中包含的上行载波多普勒频偏测量数据对上行伪码测距结果进行平滑处理；对于下行链路，接收机利用自身测量得到下行载波多普勒频偏数据进行平滑处理。该技术解决了传统的载波测量方法面临相位模糊，以及伪码测量方法精度不足的问题，综合利用了载波测量精度高和伪码测量无模糊的优势，将星地测量精度提升到毫米量级。该技术的另一个优势是能够兼容现有的非相干扩频体制，仅需在地面测控设备采用该技术，无需对星载应答机进行改造，因此在航天测控领域具有广阔的应用前景。