室内多股羽流混合运动机理模型研究进展分析

王昕 代运天 梁云

上海理工大学环境与建筑学院

0 引言

由室内热源形成的浮力羽流广泛存在，如室内热源产生的浮力羽流对空调送风气流组织的影响；火灾发生时烟气羽流对火灾探测器的影响；微粒下落时形成的微粒羽流对周围环境的影响等等，其对室内环境及其空气品质的作用影响引起了人们越来越多的关注。

国内外对浮力羽流运动机理的研究主要是建立在 Morton,Taylor ＆ Turne（1956）[1]经典羽流理论基础上，并进行相关扩展。经典羽流理论建立了点源浮力羽流的运动控制方程[2]，并对方程在稳态均匀环境下进行求解[3]，得到点源浮力羽流的基本参量。室内污染源、热源以单一点源出现的情形较少，多以多点多处的形式存在，Pera ＆ Gebhart（1975）[4]通过定义两羽流浮力通量比，得到两股等羽流和不等羽流的混合高度模型以及混合之后形成单一羽流的运动控制方程[5]。本文以此为主线，对国内外多股羽流混合运动机理模型进行分析。

1 多股羽流混合模型

以单股点源羽流控制方程为基础，对多股羽流混合后相互作用问题，很多学者对其运动机理进行了模型研究[6～7]。目前对多股羽流混合的研究主要在两个方面：一是多股羽流的混合过程，二是混合之后羽流的运动状况。Cheng,Davidson ＆ Wood（1992）[8]研究了层流线源羽流混合成单一羽流的相互作用问题，提出了一个可以限制羽流混合过程中相互卷吸的模型，发现羽流混合过程中的偏转强度要大于强羽流，但对于轴对称点源羽流的混合却没有建立相关模型进行分析；Brahimi ＆ Doan-Kim-Son（1985）[9]通过实验用温度探头和风速仪测量湍流羽流混合过程温度和速度，观察羽流从相互作用开始到完全发展成单一的自相似羽流这一过程的温度和速度变化，但这也有一定的局限性，热羽流相互作用之前没有充分发展成湍流羽流，因此只适用于纯羽流混合。

1.1 混合高度模型

Pera ＆ Gebhart（1975）[4]提出单个羽流的浮力通量和两羽流起始源的间距是描述多股羽流混合运动的重要参数。两羽流浮力通量分别为F1、F2，间距x0，定义两羽流浮力通量比：

由此得到混合高度λm的函数关系：

同时定义3个无量纲参数：

式中：x为任意高度上羽流轴心间距，m；z为羽流高度，m；b为羽流半厚度，m。

1.1.1 两等羽流混合高度模型

在相同高度的两等羽流浮力通量相等（ψ=1），使用浮力通量描述两羽流的混合，是因为浮力是羽流的驱动力，一旦羽流的驱动力一定的话，那么流量也就定了。为了更好地分析两羽流混合过程，还需要考虑两羽流之间的相互卷吸作用。Bjorn ＆ Nielsen（1995）[10]提出羽流水平卷吸速度表达式：

式中：α为羽流的卷吸系数；w为羽流的轴心速度，m/s。

假定羽流之间的卷吸只考虑水平方向上的变化，Gaskin,Papps ＆ Wood（1995）[11]认为沿着高度上的羽流间距的变化率为羽流水平速度与竖直轴线速度之比，两等羽流变化率相等，可以表述为：

在对两等羽流混合高度的求解过程中，只考虑两羽流之间的水平流动，忽略羽流的竖直方向上的变化率[12]，可以看出，羽流混合高度只与卷吸系数有关。

1.1.2 两不等羽流混合高度模型

不等羽流混合过程中，由于具有不同的浮力通量，使得其偏转量并不对称，此时：

由式（9）可知，混合高度λm与卷吸系数α成反比，故卷吸系数α选择不同，对混合高度λm的影响很大。

对比两等羽流与不等羽流的混合高度模型，不难看出，当两羽流的浮力通量比ψ=1时，不等羽流混合高度模型也适用于等羽流。对多股羽流混合高度模型进行研究，可以有效地揭示多股羽流的混合过程，为后续混合之后的运动机理研究提供依据。

1.2 混合羽流的运动控制方程

在建立了两等羽流和不等羽流的混合高度模型的基础上，羽流混合之后假定两羽流混合之后形成单一的轴对称羽流。需要建立两羽流混合之后形成单一羽流的运动控制方程，在均匀环境中，混合之后羽流的浮力通量等于两羽流浮力通量之和，只需求解其质量通量和动量通量方程。

1.2.1 两等羽流混合运动控制方程

Hunt ＆ Kaye（2005）[13]提出两个独立羽流到达混合高度后形成一个轴对称羽流，可以把两羽流的质量通量和动量通量加起来，得到混合后羽流运动控制方程：

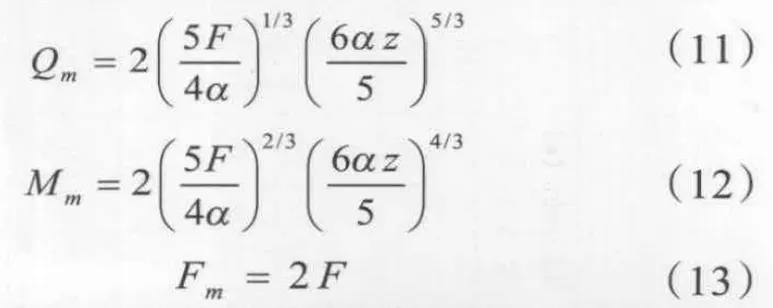
得到混合之后轴对称羽流的半厚度和轴心速度：

同时给出虚拟点源的位置：

当卷吸系数[14]时，zv=1.37x0，可知两等羽流混合后，虚拟点源位置为两羽流间距的1.37倍。

1.2.2 两不等羽流混合运动控制方程

对于不等羽流，混合之前不考虑相互卷吸作用，运动控制方程如下：

得到两不等羽流混合后的羽流半厚度和轴心速度：

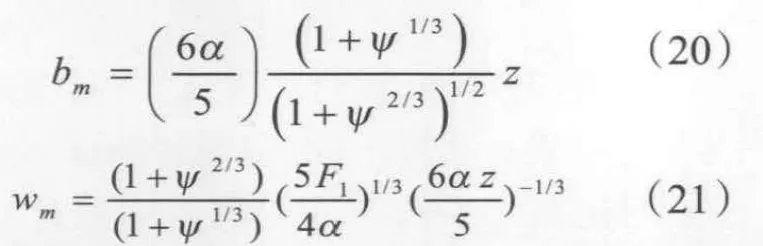
虚拟点源位置计算[15]时，浮力通量比ψ变化很大时，虚拟点源位置变化却很小，说明在计算虚拟点源位置时，质量通量和动量通量占主导作用。

建立多股羽流混合运动控制方程，是对混合羽流研究的常见手法之一，通过运动控制方程，可以了解其运动机理，进而得到其运动控制参数。同时，由运动控制方程得到混合之后的虚拟极点距，这样，就可以把复杂的多股羽流混合问题转化为相对简单的点源羽流进行考虑，使问题大大简化。

2 实例分析

假设房间内存在两点热源，间距x0=0.1m，热量分别为Q1=500W，Q2=2400W。分单股、两股等羽流（Q1=500W）与两股不等羽流（Q1=500W，Q2=2400W）分析多股羽流混合后半厚度随高度的变化关系、混合后的轴心速度与高度的关系，计算结果如图1、2所示。

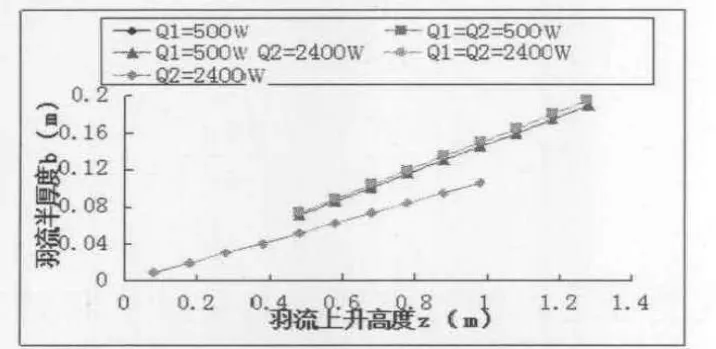
图1 羽流半厚度与高度的关系

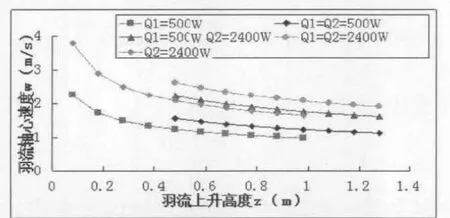
图2 羽流轴心速度与高度的关系

由图1可知，羽流半厚度随上升高度的增加而增加。在相同高度上，两等羽流混合之后半厚度大于单股羽流半厚度，但两不等羽流混合的半厚度与两等羽流混合的半厚度相差无几，同时也应证了羽流半厚度跟热源热量无关。

由图2可以看出，羽流轴心速度随上升高度的增加而增加。在0.43m以下速度衰减明显，0.43m以上速度变化减缓。在相同高度上，两等羽流混合后轴心速度大于单股羽流的轴心速度，两不等羽流混合后轴心速度大于两等羽流混合后轴心速度。说明轴心速度与热量成正相关，热量越大，轴心速度越大。

3 结论

本文对室内热源形成的多股等羽流或不等羽流的混合高度模型以及混合之后形成单一羽流的运动控制方程进行综述，并加以实例计算分析上述机理研究成果。通过分析后得知，在相同高度上，两等羽流混合之后半厚度大于单股羽流半厚度，两不等羽流混合的半厚度与两等羽流混合的半厚度相同；两等羽流混合后轴心速度大于单股羽流的轴心速度，两不等羽流混合后轴心速度大于两等羽流混合后轴心速度。对国内外多股羽流混合运动机理模型进行分析，为后续多相羽流基础模型研究与烟气控制、高大空间气流组织等应用研究提供参考。

[1]B R Morton,G I Taylor,J S Turner.Turbulent gravitational conve-ction from maintained and instantaneous sources[J].Proc.R.Soc.Lond.,1956,234:1-23

[2]W D Baines,J S Turner.Turbulent buoyant convection from a source in a confined region[J].J.Fluid Mech.,1969,37:51-80

[3]A N Campbell,S S Cardoso.Turbulent plumes with internal generation of buoyancy by chemical reaction[J].J.Fluid Mech.,2010,655:122-151

[4]L Pera,B Gebhart.Laminar plume interactions[J].J.Fluid Mech.,1975,65:250-271

[5]N B Kaye.Turbulent plumes in stratified environments:a review of recent work[J].Atmos.Ocean,2008,46:433-441

[6]N B Kaye,P F Linden.Coalescing axisymmetric turbulent plumes[J].J.Fluid Mech.,2004,502:41-63

[7]N G Kaye.Interaction of Turbulent Plumes[D].UK:University of Cambridge,1998

[8]C W Cheng,M J Davidson,I R Wood.Merging buoyant discharg-es in an ambient current[J].J.Hydraul.Res.,1992,30:361-371

[9]M Brahimi,Doan-Kim-Son.Interaction between two turbulent plumes in close proximity[J].Mech.Res.Commun.,1985,12:149-155

[10]E Bjorn,P V Nielsen.Merging thermal plumes in the internal environment[A].In:Proc.Healthy Buildings[C].1995

[11]S J Gaskin,D A Papps,I R Wood.The axisymmetric equations for a buoyant jet in across flow[A].In:Twelfth Australasian Fluid Mechanics Conference[C].1995:347-350

[12]N B Kaye,P F Linden.Coalescing axisymmetric turbulent plumes[J].J.Fluid Mech.,2003,502:41-63

[13]G R Hunt,N B Kaye.Lazy plumes[J].J.Fluid Mech.,2005,533:329-338

[14]G F Lane-serff,P F Linden,M Hillel.Forced,angled plumes[J].J.Hazard.Mater.,1993,33:75-99

[15]W K George.The Self-preservation of Turbulent Flows and Its relation to Initial Conditions and Coherent Structures-Advances in Turbulence[M].Berlin:Springer,1989