一种基于物流机器人的订单拣选排程算法设计与实现
2023-09-04姚文斌朱子欣
姚文斌 朱子欣
(浙江经济职业技术学院 浙江 杭州 310018) 2(清华大学 广东 深圳 518055)
0 引 言
物流业是国民经济的重要组成部分,现代物流的发展有利于跨产业整合资源,优化资源配置,提高产品供给时效和市场响应速度。结合人工智能、云计算、大数据、物联网等信息技术的有效应用,“互联网+物流”探索愈发成熟,与其他产业的融合能动和资源整合效能正日渐增强。2014年,亚马逊使用的Kiva系统作业效率较传统物流作业提升2~4倍,机器人时速可达48.27 km,可抬起约340 kg重的货物,准确率达到99.99%。据报道,国内智能仓储机器人产品已经在电商仓库、汽车制造商仓库等场景中应用。但是,关于如何提高机器人在订单拣选时的作业效率,这方面的研究还非常少,急需研究相关的算法。
本文以可移动货架式仓库为背景,研究该场景下基于“货到人”拣选模式的订单拣选排程问题。与传统的“人到货”模式相比,“货到人”模式一方面可以把劳动力从繁重的仓库行走、搬运中解放出来,从而有效减少对人工的依赖,另一方面还有利于通过人工智能算法指挥调度机器人来提高工作效率。由于各待拣选订单的处理顺序和各货架到达拣选台的顺序不同,在不同的仓库布局、储位分配策略下,整批全部订单完成拣选所需要的货架移动的次数也有差异。本文以单拣选台为背景,设置模型的假设条件,建立订单处理的整数规划模型,目标函数为最小化订单批次完成拣选时的货架搬运次数,用数学规划求解器软件CPLEX12.8求得小规模算例下的精确解。并设计了三种启发式算法,分别是确定订单处理次序的变邻域搜索算法(Variable Neighborhood Search algorithm,VNS)VNS-OS、确定货架到达次序的算法VNS-RS和交替求解订单和货架次序的算法AH,可求解较大规模的算例,并对计算结果进行分析,形成结论。
1 研究背景
1.1 货到人订单拣选模式
相对于传统人到货模式,货到人模式指拣货员不动,待拣选物品存储在托盘或箱子等存储设备中,由自动化输送系统从贮存区运送到拣选区,拣货员根据电子标签的提示,从存储设备中拣选出货物放入订单箱中。近年来,机器人移动履约系统(Robotic Mobile Fulfillment System ,RMFS)这种新型货到人订单拣选系统,逐渐进入大众视野。它由Kiva systems、Swisslog等公司推向市场,并于2014年开始被亚马逊应用于仓库,适用于需求波动明显的多种中小件商品的电商配送中心。RMFS系统的前期投入费用高昂,涉及仓储策略复杂,且目前在商超、医药、化妆品、3C等应用场景下的拣选效率提升效果不明显,技术落地有一定难度。
RMFS系统的整体优化目标是最小化人力费用和设备支出,涉及储物货架选择、货架储位分配、订单分配、补货分配和机器人分配等问题。Yuan等[1]建立开放排队模型,研究RMFS系统的性能。Boysen等[2]提出集束搜索启发式算法,优化小规模订单和待拣选货架的排序,以减少所需机器人数量。Yuan等[3]构建排队网络模型,通过数值分析计算订单拣选时间来评估系统性能,得到机器人的最佳数量和速度。Lamballais等[4]建立单队和多队订单的排队网络模型,评估RMFS系统下不同的仓库布局和机器人分区策略。Zou等[5]研究RMFS系统的电池管理问题,建立半开放排队网络(SOQN)来评估系统性能。Kumar等[6]研究RMFS系统的路径规划问题,设计多种仓库布局下无碰撞路径的算法。Roy等[7]基于多级封闭排队网络模型,研究RMFS系统的存储区域的拣货和补货流程。Lamballais等[8]引入排队模型,设计优化每个存储单位对应的货架数、拣选站与补货点数量比和各货架的补货点的算法。现有关于货到人订单拣选的研究大多是从仓库布局设计或者局部运作策略的角度对拣选系统的效率进行评估,但是这些研究不能给出操作层面的订单拣选计划,即订单作业顺序和货架的供应顺序。虽然文献[2]研究了作业层的订单拣选计划问题,但是其采用的是集束搜索启发式算法,这种算法受集束宽度参数的影响较大,而本文则提出一种可变邻域搜索算法,这种元启发式算法已在很多仓库作业问题研究中被证明有效。
1.2 订单排序问题
目前,国内外围绕优化订单排序的研究较少,多数基于传统人到货拣选模式,且多与订单分批、路径规划等策略同时进行研究。Zhang等[9]围绕在线订单批处理和排序问题,以最小化周转时间为目标,讨论拣货员数量对系统拣选效率的影响。Boysen等[10]研究移动货架仓库系统的订单拣选排序问题,讨论开放过道数量对拣选作业的影响,目标是提高空间利用率和减少拣选人力消耗。Scholz等[11]考虑订单到期日,提出变邻域下降算法,以最小化系统总延迟为目标,求解订单分批、批次分配及排序、路径规划的整合优化策略。Boysen等[12]研究电商仓库的自动分拣问题,提出两阶段基于动态规划的订单处理算法,目标是最小化释放顺序中的订单分布。Chen等[13]研究考虑客户订单延迟的订单组批、排序和路径规划问题,建立非线性混合整数规划模型,提出了混合编码遗传算法和蚁群优化相结合的算法。
1.3 储位分配问题
储位分配问题研究如何将入库货物分配到仓储区的货位上,优化储位分配可以有效缩短拣货作业时长,降低物料搬运成本,提高空间利用率。目前,基于人到货拣选模式的储位分配问题的研究成果较多,但不能直接应用于货到人模式下。Pan等[14]研究多拣选员pick-and-pass系统的储位分配问题,提出以减少缺货和平衡各拣选区工作量为目标的启发式算法。Guo等[15]研究在考虑储货区空间消耗的单位装载仓库下,对比叉车在单指令模式下随机、全周转率和基于类的三种存储策略对拣货走行距离的影响。
1.4 任务调度问题
仓库管理中的任务调度问题主要包括机器人任务分配、订单任务分配、补货任务分配等,目的是提高系统拣选效率,平衡任务负载。Elango 等[16]旨在解决RMFS系统的多机器人任务分配问题,用k-means算法实现将任务聚类、计算机器人走行成本和机器人分配,实现最小化多机器人走行距离和均衡工作负荷的目标。Zhou等[17]针对智能仓库的多机器人任务分配问题,提出以最小化走行距离和平衡工作负载为目标的平衡启发式机制。
1.5 变邻域搜索算法
变邻域搜索算法(VNS)是一种求解组合优化和全局优化问题的元启发式算法,基本思想是在下降阶段系统地改变邻域以找到局部最优解,在扰动阶段跳出相应谷[18]。目前,应用VNS算法求解仓储管理问题的文献数量不多,且主要基于人到货的拣选场景。Menendez等[19]讨论人到货拣选模式下订单的批处理及排序问题,提出变邻域搜索算法,目标是最小化订单的延误惩罚成本。Yang 等[20]研究共享存储策略下多载具自动化存取系统的储位分配和存储检索调度的联合优化问题,允许检索操作产生的空位重用,提出求解大规模算例的变邻域搜索算法。Menendez等[21]围绕人到货拣选模式下最小-最大订单批处理问题,提出并行变邻域搜索算法,目标是最小化所有订单批次的最大拣选时间。
综上所述,现有的订单排序、储位分配、任务调度等方面的研究,虽然与本文有一定的重叠,但并不是针对“货到人”这一应用场景的,因而问题区别较大;同时,针对“货到人”场景,缺乏适用于操作层的订单拣选算法,因此,本文对这一问题开展研究。
2 模型建立
2.1 符号说明
模型的符号说明如表1所示。

表1 符号说明
2.2 基本假设
本文研究的拣选台订单处理问题,将基于以下基本假设展开求解:
(1) 假设仓储区采取共享存储策略,即一种货物可分散存储在多个货架上。
(2) 假设货架上货物数量充足,不考虑缺货情况。
(3) 不考虑机器人行走过程中的堵塞。
(4) 不考虑拣选台之间的相互影响。
(5) 假设订单的活跃状态转换发生在货架改变之前,即当本回合有活跃可拣选订单完成拣选后,下一回合补入的新活跃订单可利用本回合活跃货架拣选货物。
2.3 整数规划模型建立
建立基于货到人系统的拣选台订单处理的整数规划模型如下:
(1)
s.t.
(2)
(3)
yj,t+yj,t+d≤yj,t+1+1
∀t=1,2,…,T,d=2,3,…,T-t,∀j=1,2,…,N
(4)
(5)
∀i=1,2,…,M,∀j=1,2,…,N,∀t=1,2,…,T
(6)

(7)
xrt∈{0,1} ∀r=1,2,…,R,∀t=1,2,…,T
(8)
yjt∈{0,1} ∀j=1,2,…,N,∀t=1,2,…,T
(9)
zijt∈{0,1} ∀i=1,2,…,M,∀j=1,2,…,N,
∀t=1,2,…,T
(10)
式(1)是最小化完成所有订单拣选时货架的总搬运次数,其中Φt由式(7)定义,表示到达拣选台的货架的改变次数。式(2)限制拣选台可同时拣选货架的最大数量。式(3)限制拣货员最多可同时处理B个待拣选订单。式(4)确保每个订单必须在连续的回合期间被拣选。式(5)确保全部订单的所有货物必须都被拣选完成。式(6)表示当且仅当现回合下订单是活跃可拣选状态,且所需货物也储存在当前活跃货架中时,该待拣选货物才能被拣出。式(8)、式(9)和式(10)定义xrt、yjt和zijt为0-1变量,其中xrt记录了各回合中活跃状态订单包含的待拣选货物种类的拣选情况,由xrt可得出货架排序RS为所有回合中首次取1时对应的货架编号r的顺序排列集合,由yjt可得出订单处理排序OS为所有回合中yjt首次取1时对应的订单编号j的顺序排列集合。
3 算法设计
随着算例规模的增大,精确算法求解数学模型所需时长远超出可行范围,因此本文设计了三种算法来求解更大规模算例,分别为确定订单处理次序的算法VNS-OS、确定货架到达次序的算法VNS-RS和交替求解订单和货架次序的算法AH。
3.1 确定订单排序的订单处理问题
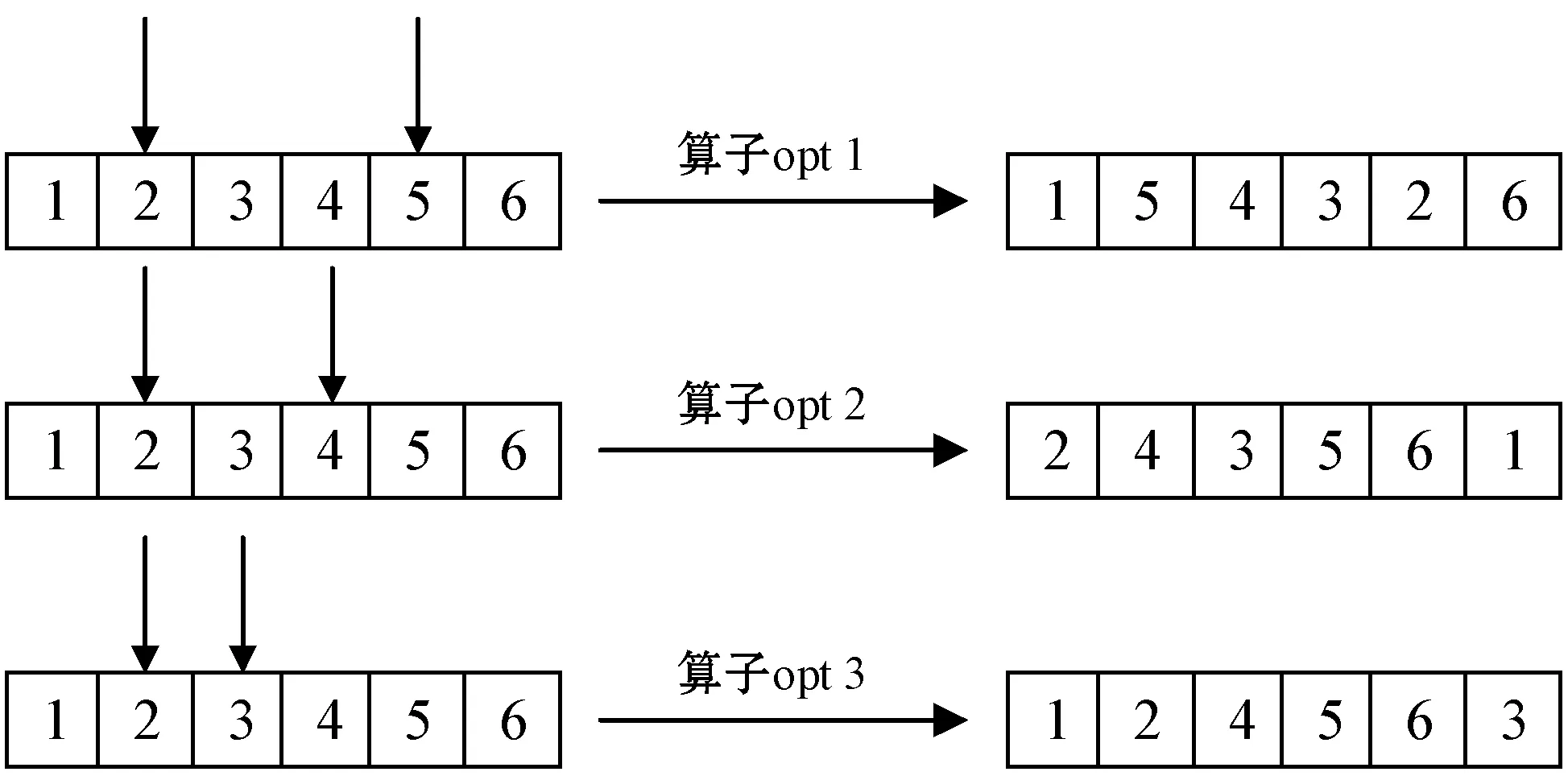
算法VNS-OS的思路是先确定待拣选订单处理排序,再根据给定的订单排序求得对应货架搬运总次数最少的货架排序。其中,待拣选订单处理排序通过算子Shaking、opt1、opt2和opt3进行变换,通过函数GreedyOS求解出对应的最优货架排序,VNS-OS算法如算法1所示。
算法1VNS-OS算法
输入:抖动邻域Ns,VND邻域集合Nl=1,2,3,设置MaxVNDIteration和MaxIteration。
输出:RS记录当前最优货架排序,首列记录最少货架搬运次数,OS记录当前最优订单排序。
生成初始解:由初始OSet和函数GreedyOS求得初始货架排充RS。
1.OS=OSet;
//设初始订单排序为OSet
2.RS=GreedyOS(OS);
//由函数GreedyOS求得初始货架排序RS
3.k=0;
//设VND算法框架的初始迭代次数为0
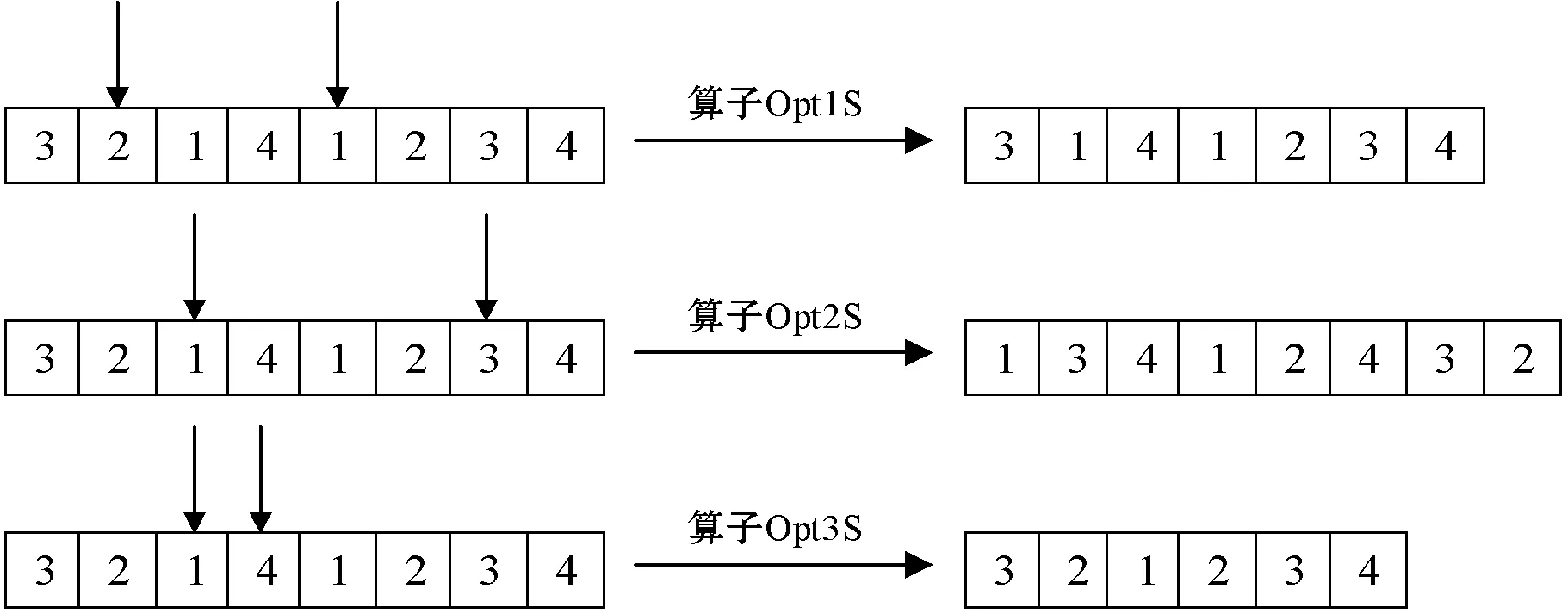
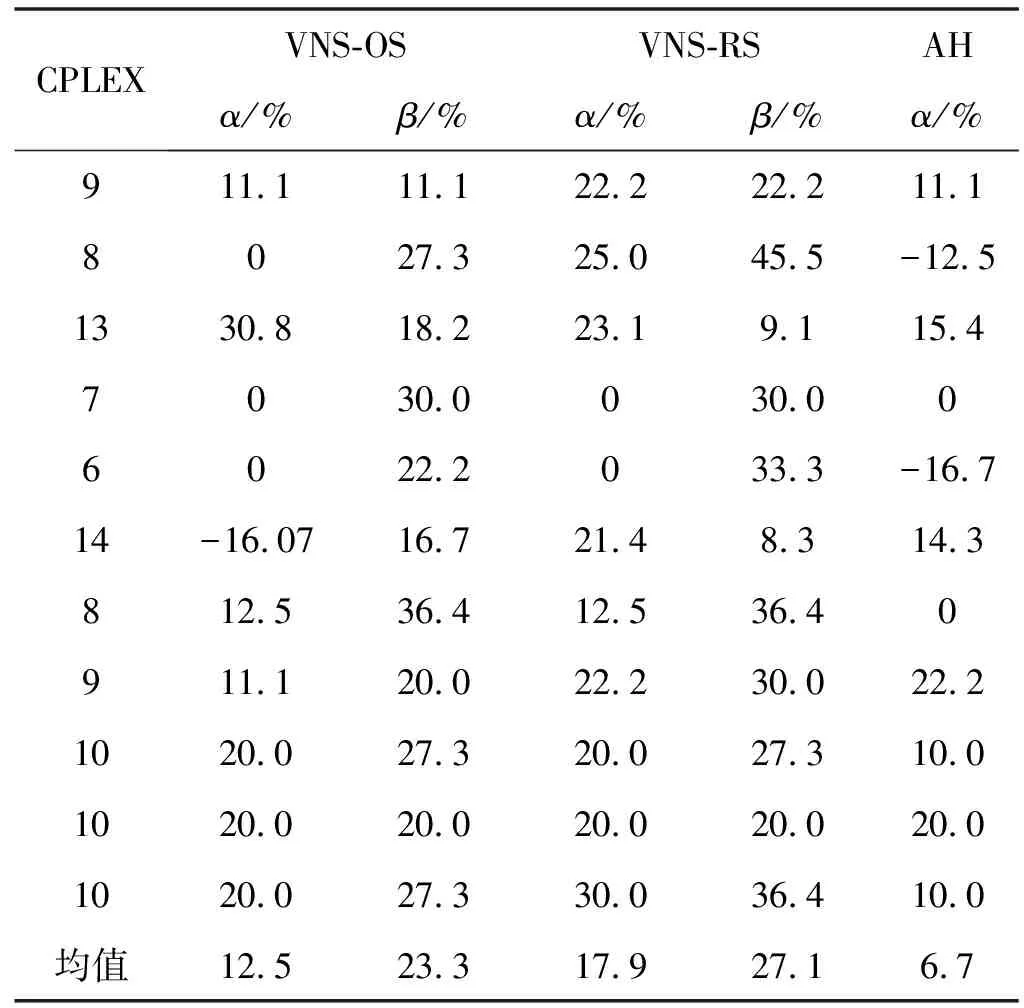
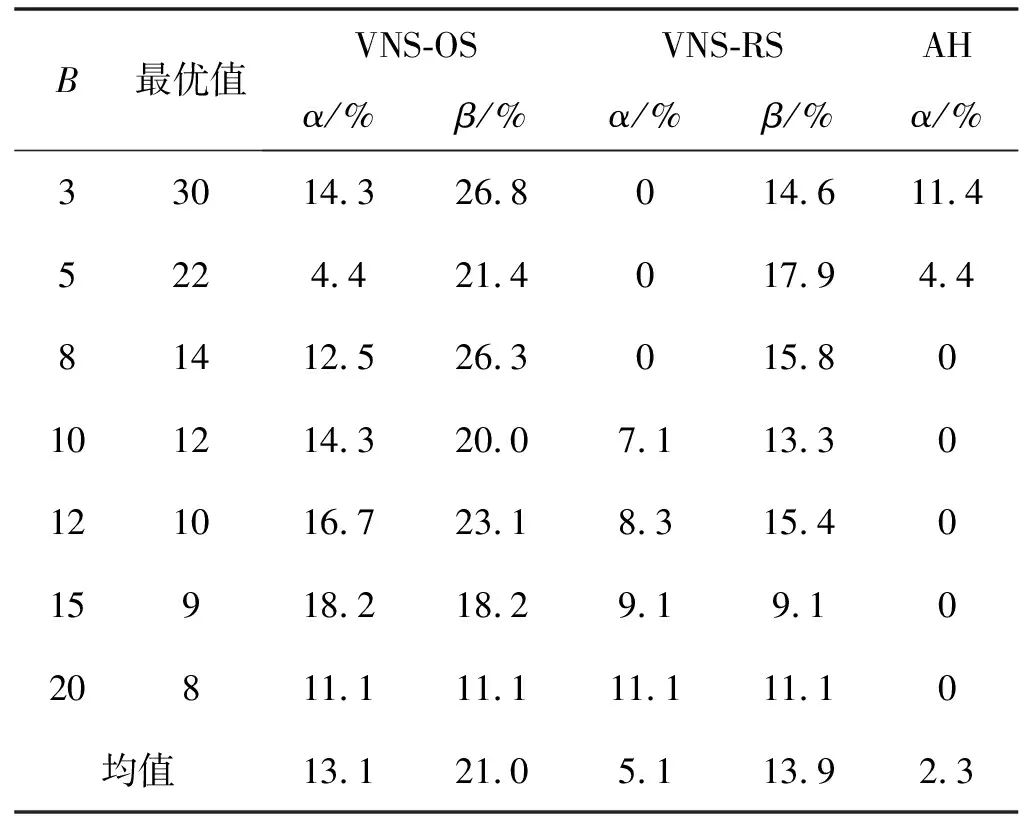
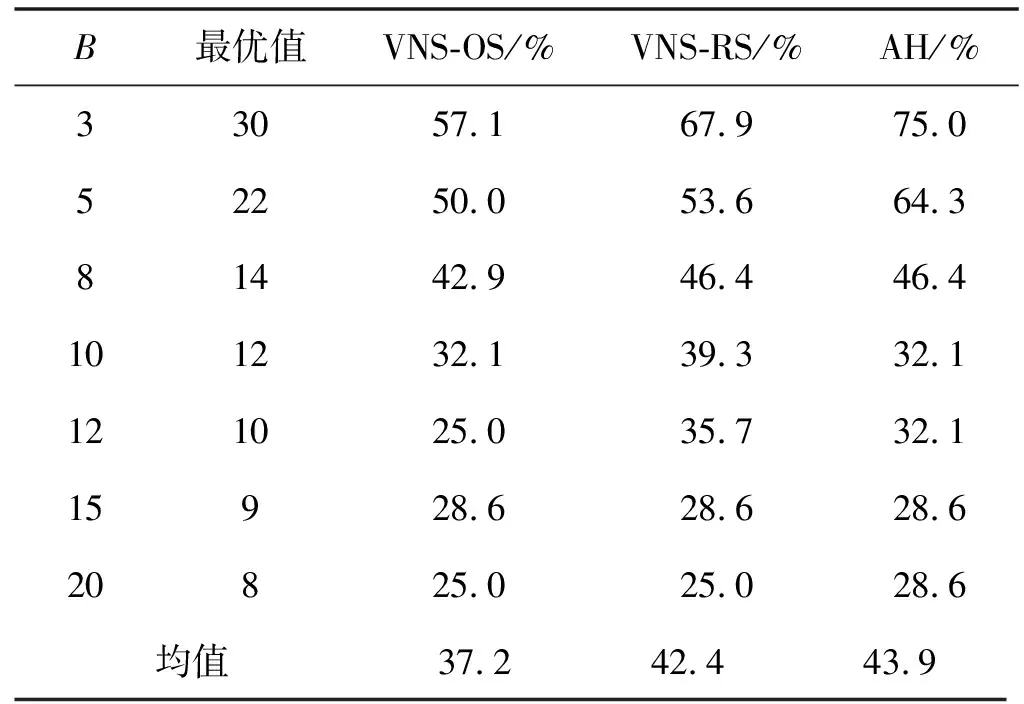
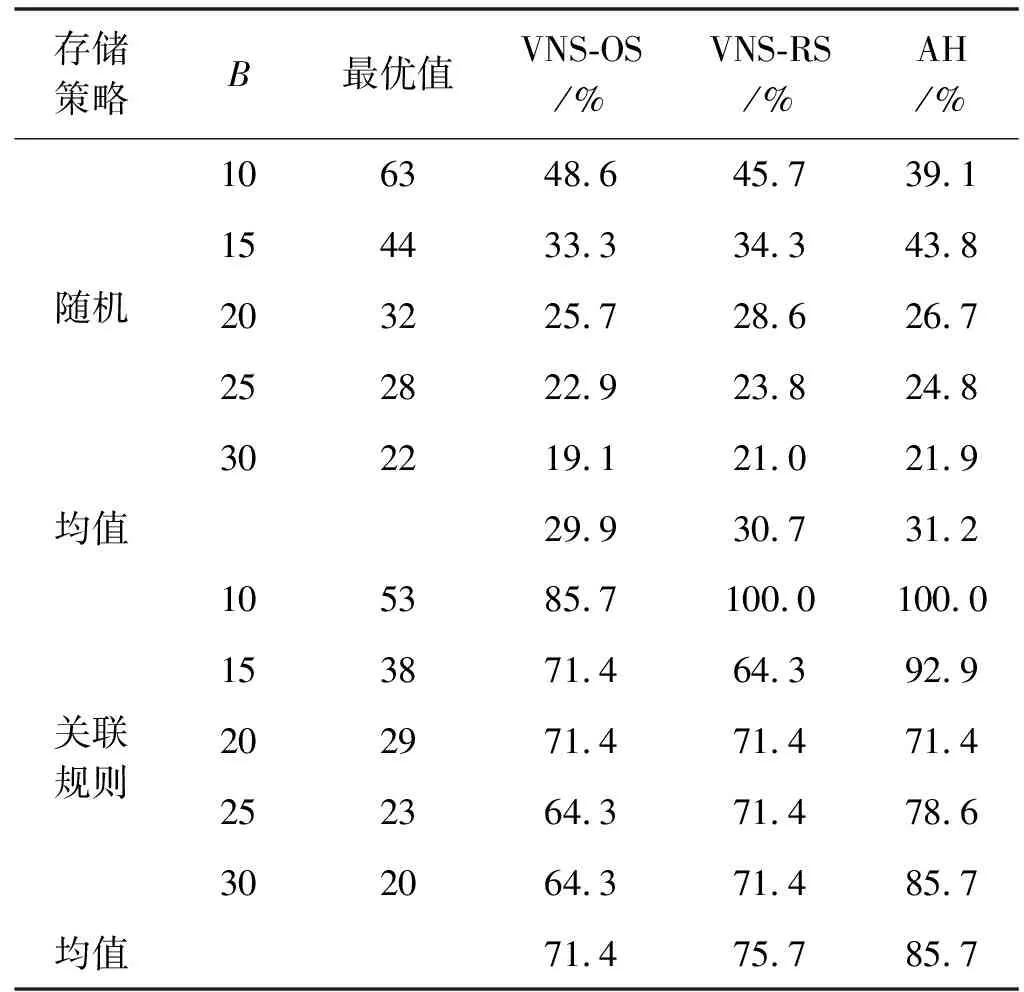
4.whilek //MaxVNDIteration为VND算法框架最大迭代次数 5.flip=1; //从VND内邻域Nl开始局部搜索 6.whileflip //依次在邻域N1、N2、N3进行局部搜索后跳出VND 7. //抖动阶段 8.OSSolution=Shaking(OS); //执行算子Shaking,生成Ns(OS)随机邻域解 9.OptimalRackSeq=GreedyOS(OSSolution); //求解对应货架排序 10. //进入VND算法框架的局部搜索阶段 11. ifflip==l //flip指示进入VND框架内对应邻域Nl进行局部搜索 12. [OSSolution,OptimalRackSeq]=optl(OSSolution,OptimalRackSeq); 13. end 14. //更新最优解: 15. ifOptimalRackSeq(1) //当经历VND所得解优于当前最优解时 16.OS=OSSolution; //更新OSSolution为当前订单最优排序OS 17.RS=OptimalRackSep; //更新OptimalRackSeq为当前货架最优排序RS 18. continue //如果在本邻域找到更优解,则跳回扰动邻域Ns进行搜索 19. else 20.flip=flip+1; //若在本邻域未找到更优解,跳到下个邻域Nl继续搜索 21. end 22. end 23.k+k+1; //记录VND算法框架的迭代次数 24. end 按初始订单处理排序排列的订单集合为OSet,通过邻域变换生成新的订单排序,包括扰动阶段和局部搜索阶段。扰动阶段有算子Shaking,实现在N个订单标号排序中任意选择2个订单行调换拣选次序的变换。图1展示了N=6时订单排序经历算子Shaking前后的变换过程,其中箭头标识所选插入点。 图1 算法VNS-OS扰动阶段邻域算子Shaking变换示例 局部搜索阶段有opt1、opt2和opt3三个算子,其中算子opt1实现在N个订单标号中取随机选择的2个插入点间进行区间反转的变换,算子opt2实现在N个订单标号中取随机选择的2个插入点塞入新序列头部,其余标号按原序列依次排列,算子opt3实现在N个订单标号中取随机选择的2个相邻插入点,将数字大的插入点后面的订单标号插入两点之间。图2展示了N=6时订单排序分别经历算子opt1、opt2和opt3前后的变换过程。 图2 算法VNS-OS局部搜索阶段邻域算子变换示例 函数GreedyOS用于求解当前待拣选订单处理排序下的使所有订单拣选完成的货架搬运总次数最小的货架排序。它的基本思路是,为了使全部订单拣选完成时的货架搬运总次数最小,即要使每回合从当前活跃货架上拣出的货物最多,在每回合选择与当前活跃订单总差异最小的为活跃货架。其衡量标准为货架内货物种类组合与当前活跃订单行的差异,如式(11)所示,由于两者均为用逻辑语言表达货物种类包含关系的0-1行向量,故两者的差异用附带条件的曼哈顿距离公式表示。 (11) 算法VNS-RS的思路是先确定到达拣选台的货架排序,再根据当前活跃货架内的货物种类组合决定本回合的活跃订单,以各待拣选订单依次转变为活跃状态的顺序,作为使货架搬运总次数最少的待拣选订单处理排序。其中,货架到达拣选台的排序通过算子Shaking1、opt1S、opt2S和opt3S进行变换,通过函数GreedyRS求解出对应的最优订单排序,VNS-RS算法如算法2所示。 算法2VNS-RS算法 输入:N,R,OSet,抖动领域Nk,k=1,VND邻域集合Nl,l=1,2,3,设置MaxVNDIteration和MaxIteration。 输出:RSsolution记录最优货架排序,OSsolution记录最优订单排序,首列为最少货架搬运次数。 生成初始解:初始订单排序为OSet,由函数GreedyOS求得初始货架排序InitialRS,记此时货架搬运次数为InitialScore,再加上n个{1:R}构成RSsolution。 1.OSsolution=[InitialScore,1:nOrder]; //设初始订单排序为OSet 2.RSsolution=GreedyOS(OSet); //通过函数GreedyOS求货架初始排序RSsolution 3.K=0; //设VND算法框架的初始迭代次数为0 4.whileK //MaxVNDIteration为VND算法框架最大迭代次数 5.flip=1; //从VND框架内邻域Nl开始局部搜索 6.whileflip //依次在邻域N1,,N2,N3进行局部搜索后跳出VND 7. //抖动阶段 8.OptimalRackSeq=Shaking1(RSsolution); //生成Ns(RSsolution)随机邻域解 9.OptimalOrderSeq=GreedyRS(OptimalRackSeq); //求解订单排序 10. //进入VND算法框架的局部搜索阶段 11. ifflip==l //flip指示进入VND框架内对应邻域Nl进行局部搜索 12. [OptimalRackSeq,OptimalOrderSeq]=optl(OptimalRackSeq,OptimalOrderSeq); 13. end 14. //更新最优解: 15.ifOptimalOrderSeq(1) //若VND所得解优于当前最优解 16.OSsolution=OptimalOrderSeq; //更新当前订单最优排序为OSsolution 17.RSsolution=OptimalRackSeq; //更新当前货架最优排序为RSsolution 18. continue //如果在本邻域找到更优解,则跳回扰动邻域Ns进行搜索 19. else 20.flip=flip+1; //若在本邻域未找到最优解,跳到下个邻域Nl继续搜索 21. end 22. end 23.K=K+1; //记录VND算法框架的迭代次数 24. end 通过函数GreedyOS求解订单处理排序为OSet时的货架排序InitialRS,之后通过扰动阶段和局部搜索阶段的邻域变换生成新的货架排序,当变换后货架排序中出现相同的相邻货架标号,则删去重复标号。扰动阶段有算子Shaking1,实现在当前货架排序中任意选择2个货架标号调换次序。图3展示了初始货架排序为{3,2,1,4}(R=4,插入点在排位1-7范围内选取)时货架排序经历算子Shaking1前后的变换过程。 图3 算法VNS-RS扰动阶段邻域算子Shaking1变换示例 局部搜索阶段包括算子opt1S、opt2S和opt3S,其中算子opt1S实现在当前货架排序中取随机选择的2个插入点间进行区间反转,算子opt2S实现在当前货架排序中取随机选择的2个插入点塞入新序列头部,其余货架标号按原序列依次排列,算子opt3S实现在当前货架排序中取随机选择的2个相邻插入点,将排位靠后插入点后面的货架标号插入两点之间。图4展示了初始货架排序为{3,2,1,4}(R=4,插入点在排位1至7范围内选取)时货架排序分别经历算子opt1S、opt2S和opt3S前后的变换过程。 图4 算法VNS-RS局部搜索阶段邻域算子变换示例 函数GreedyRS用于求解当前到达拣选台的货架排序下的确保全部订单完成拣选的货架搬运总次数最小的订单处理排序。其基本思路与函数GreedyOS类似,在每回合选择与当前活跃货架的差异最小的订单转为活跃状态。 基于对上述两个子问题的思考,设计交替确定订单和货架排序的算法AH。算法AH的基本思路为先计算各货架与当前活跃订单的差异,取总差异最小的为本回合活跃货架,再取与当前活跃货架差异较小的订单为活跃订单,交替来确定订单和货架排序。最终得到R组解订单排序AOSSeqSet和对应货架排序ARSSeqSet,取R组解中完成所有订单拣选时所需货架搬运次数最少的为最优订单排序AOSSeq和最优货架排序ARSSeq,AH算法如算法3所示。 算法3AH算法 输入:N,M,R,B,OSet,RSet。 输出:AOSSeqSet,ARSSeqSet,生成R组解。 1. //首回合依次取各货架为首个活跃货架,分别再取当前货架 //差异较小的为首批活跃订单,生成R组解 2. AT=2; //记录当前货架搬运次数 3.whilelength(finishedOrderID) //循环终止条件为全部订单都完成拣选 4. //计算各订单与当前活跃货架的差异,取差异较小的 //订单为活跃订单 5. fori=1:length(pickingOrderID) //遍历当前活跃订单 6. forp=1:nRack //遍历所有货架 7.distance=0; 8. forj=1:nSku //遍历所有货物种类 9. ifCurrentOrderSet(pickingOrderID(i),j)>0 10. //用带条件的曼哈顿距离公式来计算货架与订单行的差异 11. [~,CurrentRackID]=min(pickingDis); //取总差异最小的为活跃货架 12.ARSSeq(1)=AT; //ARSSeq首列记录当前货架已搬运次数 13.ARSSeq(AT+1)=CurrentRackID; //ARSSeq末列记录当前活跃货架 14. //检查当前活跃订单是否有拣选完成的 16.pickedOrderID=pickingOrderID(rr); //记录本回合完成拣选的订单标号 17.pickingOrderID=setdiff(pickingOrderID,pickedOrderID); //更新活跃订单ID 18.finishedOrderID=[finishedOrderID,pickedOrderID]; //更新已完成订单ID 19.DD=setdiff(1:nOrder,finishedOrderID); 20. InActiveOrderID=setdiff(DD,pickingOrderID); //更新剩余未拣选订单ID 21. //如有,按当前订单处理排序补足至min(B,剩余待拣选 //订单数)个活跃订单 22. //计算本回合拣选过后的CurrentOrderSet,将拣选完成 //订单行标记为10 000行 23. //本回合新补进的活跃订单进行当前货架的拣选 24.AT=AT+1; //每搬运一次货架AT增加1 25. end 与本文研究的问题最直接相关的是文献[2],但该文未提供具体的算例数据,无法直接对比本文算法与该文提出的集束搜索算法,但该文指出了算例中参数的取值范围,并讨论了其合理性。本文根据文献[2],分别随机产生了一组小规模、一组中规模和一组大规模算例。其中小规模算例可以直接用整数规划求解器CPLEX利用问题的数学模型(见2.3节)进行求解,得到问题的最优解或者近似最优解,从而为评价本文提出的VNS算法提供依据。中等规模和大规模是指逐步加大订单数、货架数和SKU数等,以进一步加大搜索空间和计算强度,通过与算法初始解的对比来进一步测试VNS算法的有效性。首先介绍其中的订单集和货物集的生成方法。订单集合OSet由函数OrderSet生成,输入参数为待拣选订单总数N和货物种类数M。假设各种货物在所有订单中出现的次数服从均值为λi的泊松分布,i值取1到M的正整数。各货物对应的λi之间相对大小排序随机产生,限制所有取值服从[0.2N,0.8N]的均匀分布,确保OSet中无空订单行的出现。 本文考虑了两种储位分配策略:随机储货和按货物间关联规则储货。其中,随机储货策略由函数RackSkuSet实现,输入参数为货物种类数M、货架种类数R和x,其中M-x限制所有货架中允许出现的最多货物种类数。所有种类的货物一定储存在至少一个货架内,确保各货架内货物种类组合之间不存在包含关系,且互不相同。 而按货物间关联规则的储位分配策略,本文通过引入智能算法Apriori从频繁项集中挖掘出待拣选订单中各种货物之间的关联规则。频繁项集指经常同时出现的元素集合,其定义包括支持度和置信度两个重要指标,其定义如式(12)和式(13)所示。 (12) (13) Apriori原理的核心理论为,如果一个元素是非频繁项,那么它的超集也是非频繁项集。这样,Apriori算法可以避免项集数量的指数增长,进而在合理时间范围内寻找到频繁项集。Apriori算法如算法4所示。 算法4Apriori算法 输入:OSet。 输出:关联规则文档rules.txt。 1.minSup=0.3; //设置最小支持度 2.minConf=0.3; //设置最小置信度 3.nRules=1 000; //设置最大输出关联规则数量 4.sortFlag=1; //按照支持度从大到小的排序依次输出关联规则 5. //调用Apriori算法寻找待拣选订单内货物种类间的关联规则 6. [Rules,FreqItemsets]=findRules(OSet,minSup,minConf,nRules,sortFlag,code,rulefile); 7. //生成候选项集 8. //对待拣选订单集合的每个订单行 9. //对每个由货物种类组成的候选项集 10. //检查候选项集是否为订单行的子集 11. //如果是,则该候选项集计数加1 12. //对各候选项集 13. //若其支持度大于最小支持度,则保留该项集 14. //返回所有频繁项集 15. //当集合中项的个数>0 16. //构建候选项集列表,初始n=1 17. //计算候选项集支持度,删除非频繁项集 18. //构建由n+1项组成的候选项集的列表 19. //从频繁项集中挖掘关联规则 在小规模算例下,通过对比CPLEX在10分钟内求得的整数规划模型的解,验证算法VNS-OS、VNS-RS和AH的有效性。参数设置为N=20、M=5、R=10、B=3,采用随机储货策略,共10个货架储存不同的两两货物种类组合。表2列出了各算法求得的搬运次数,其中第一列是用CPLEX求得的搬运次数,第2、4、6列中α分别表示用VNS-OS、VNS-RS、AH算法求得的搬运次数的改进百分比(正值表示降低),第3、5列β表示与初始解的搬运次数改进百分比(正值表示降低)。 表2 小规模算例计算结果 分析表2,在小规模算例下,可以得出:对比CPLEX耗费10分钟求得的已知最优解,三种算法的平均求解质量更优,并且平均求解优化效果排序为VNS-RS>VNS-OS>AH,平均优化程度分别为17.9%、12.5%和6.7%,从而证明了三种算法的有效性。对于算法VNS-OS和VNS-RS,最终解对比其初始解的平均优化程度分别为23.3%和27.1%,证明VNS算法对于订单处理排序和货架排序的优化效果明显。VNS-RS、VNS-OS和AH求解小规模算例的平均运行时间分别为26 s、72 s和1 s,均比CPLEX软件求解时间要短。 在中等规模算例下,参数设置为N=50,M=8,R=28,B在3~20之间取值。采用随机储货策略,共28个货架储存不同的两两货物种类组合。 分析表3,在中等规模算例下可以得出:对比三种算法求得的最优解,平均求解优化效果排序为VNS-OS>VNS-RS>AH,平均优化程度分别为13.1%、5.1%和2.3%,同时算法AH在B取值较小时求解质量较优,算法VNS-RS在B取值较大时求解质量较优。算法VNS-OS和VNS-RS的最终解对比其初始解的平均优化程度分别为21.0%和13.9%,证明VNS算法对订单处理排序和货架排序的优化效果明显。VNS-RS、VNS-OS和AH求解中等规模算例的平均时间分别为89 s、155 s和2 s,耗时较短。 表3 中等规模算例计算结果 在大规模算例下,参数设置N=100,M=15,R=105,B在10~30之间取值。分别采用随机和按关联规则的储位分配策略,随机储货策略为共105个货架储存不同的两两货物种类组合,按Apriori算法计算出的置信度最高的14条关联规则将货物存储在14个不同货架中。 分析表4,在大规模算例下,可以得出:相比于三种算法求得的最优解,平均求解优化效果排序为VNS-OS>VNS-RS>AH,平均优化程度分别为9.3%、5.7%和1.4%,同时算法AH在B取值较小时求解质量较优,算法VNS-RS在B取值较大时求解质量较优。对于算法VNS-OS和VNS-RS,最终解相比于其初始解的平均优化程度分别为14.0%和10.6%,证明VNS算法对订单处理排序和货架排序的优化效果明显。VNS-RS、VNS-OS和AH求解大规模算例的平均时间分别为135 s、141 s和13 s,耗时适中。 表4 大规模算例计算结果 综合不同规模算例的计算结果,总结出三种算法求解质量较好的条件,即当算例规模较小或算例规模较大且B取值较大时,选择算法VNS-RS求解质量较高;当算例规模较大且B取值较小时,选择算法AH求解质量较高且耗时短;算法VNS-OS整体的求解质量稳定,性能最优。 基于对不同规模算例的求解结果,研究全部订单完成拣选时货架总搬运次数和货架利用率受单拣选台可同时处理最大订单数和不同储位分配策略的影响。 分析表5,可以得出:在随机储位分配策略下,三种算法中,算法VNS-OS求得的平均货架利用率最小(37.2%)。该策略下,货架平均利用率较低,仅利用到近四成货架,并且货架利用率随拣选台可同时处理的最大订单数B值增加而降低。货架搬运次数随B值增加而减少,但下降幅度逐渐变小,说明B取值不是越大越好。随着可同时处理的最大订单数增加,所需货架搬运次数减少的收益增幅逐渐降低,但同时人力和设备成本却在增加,因此,应当取合适大小的订单处理批量实现系统整体效率的优化。 表5 货架搬运次数和货架利用率随B值变化情况 按照随机和关联规则的存储策略分别对相同算例求解。如表6所示,首列标注了各组算例采取的储位分配策略,可以得出:对比随机储货策略,按关联规则储货的平均货架利用率约为随机储货的2.4倍,所需货架搬运总次数平均减少12.7%,说明按关联规则储货可以节省大量货架,在减少货架搬运次数的同时提高货架利用率,优于随机储位分配策略。 表6 货架搬运次数和货架利用率随B值变化情况 本文关注智能物流背景下的货到人拣货系统,研究基于物流机器人的订单拣选排程算法及其实现,是“货到人”拣选模式的理论研究和应用。本文在考虑单拣选台可同时处理的最大订单数和货架内货物组合规则的前提下,建立了求解拣选台订单处理的整数规划模型。接着分别从先确定订单处理次序和货架到达次序两个角度,设计了VNS-OS算法和VNS-RS算法,进一步设计了交替求解订单和货架排序的AH算法,证明了算法的有效性和准确性。最后结合算例计算结果,在完成所有订单拣选和所需货架搬运总次数最少的前提下,分析单拣选台可同时处理的最大订单数、储位分配策略(随机分配、按货物间关联规则分配)对拣选效率和货架利用率的影响,为可移动货架式仓库的实际运营者提供有利于提升系统拣选效率的仓库管理建议。 随着近年来可移动式货架仓库在电商、快消品、药品等多类场景下的应用和发展,RMFS系统的实际运行还有很多值得深入研究和综合考虑的问题。未来可以考虑货架内货物经拣选后出现缺货的情况,研究合适的补货策略,还可以考虑多个拣选台共同处理待拣选订单的情况。未来可以综合考虑结合仓库布局、路径规划、机器人小车电池管理等问题,提升仓库的拣选效率,减少系统总支出。
3.2 确定货架排序的订单处理问题

3.3 交替确定订单和货架排序的订单处理问题
4 算 例
4.1 基本参数设置
4.2 结果分析

4.3 敏感性分析
5 结 语
