Excel中不可见浮点数误差的来源探究
2023-09-04李镇冰唐启奎
李镇冰 唐启奎
(青海省药品检验检测院青海省中藏药现代化研究重点实验室 青海 西宁 810016)
0 引 言
Excel不仅是电子表格软件,更是数据处理软件,使用者可以利用其丰富的功能和强大的函数库以较低的学习成本实现对复杂数据的分析处理,因此在统计、工程、计量检测等领域都有着广泛的应用[1-3]。
但在使用Excel进行涉及小数的操作时,可能会遇到一些“莫名其妙”的困扰:比如计算结果与预期结果之间可能存在微小的差异——公式“=4.1-4.2+1”的结果在小数位数足够多时显示为“0.899 999 999 999 999”;又或者看上去相同的两个数值,Excel却认为它们是不同的——公式“=MATCH(0.1+0.2-0.1,0.1+(0.2-0.1),0)”返回的结果是“#N/A”,加法结合律似乎都失效了。
对于单纯的计算而言,这只是数值的微小差异,通常并不会带来严重的问题,但是涉及比较、查找等操作时,则可能导致错误的结论,因而存在较大的隐患[4]。
第一种误差是可见的,对于具有一定计算机基础、了解数据类型的用户而言也是易于理解的,其产生的原因是十进制小数转换为二进制浮点数时的精度损失[5];第二种误差是不可见的,有学者认为是由于单元格中所显示的十进制数和系统内部存放的二进制浮点数并不完全一致,存在一定的误差[6],但未提供这一说法的依据。笔者最初对此有些疑惑,因为微软宣称Excel严格遵循IEEE 754标准[7],运算和存储都基于64位二进制双精度浮点数,相当于十进制的15位有效数字精度,而且可以很容易地确认Excel中显示的精度也是15位有效数字(在单元格中输入“0.123 456 789 012 345 678 9”,结果会变为“0.123 456 789 012 345”),即存储和显示精度似乎是一致的,不应该存在“所见”与“所得”不一致的情况。
本文以示例的形式对Excel中可见与不可见浮点数误差的相关问题进行深入探讨,并给出不可见误差来自于存储和显示精度差异的直接证据。所用Excel版本为2019专业增强版(64位)。
1 构造小数数列
采用以下方式在sheet1-sheet4工作表的A列分别构造出公差为0.01、范围为-2.59~2.59的等差数列,并在B列分别给出对应的修约后的数据。结果如表1所示。
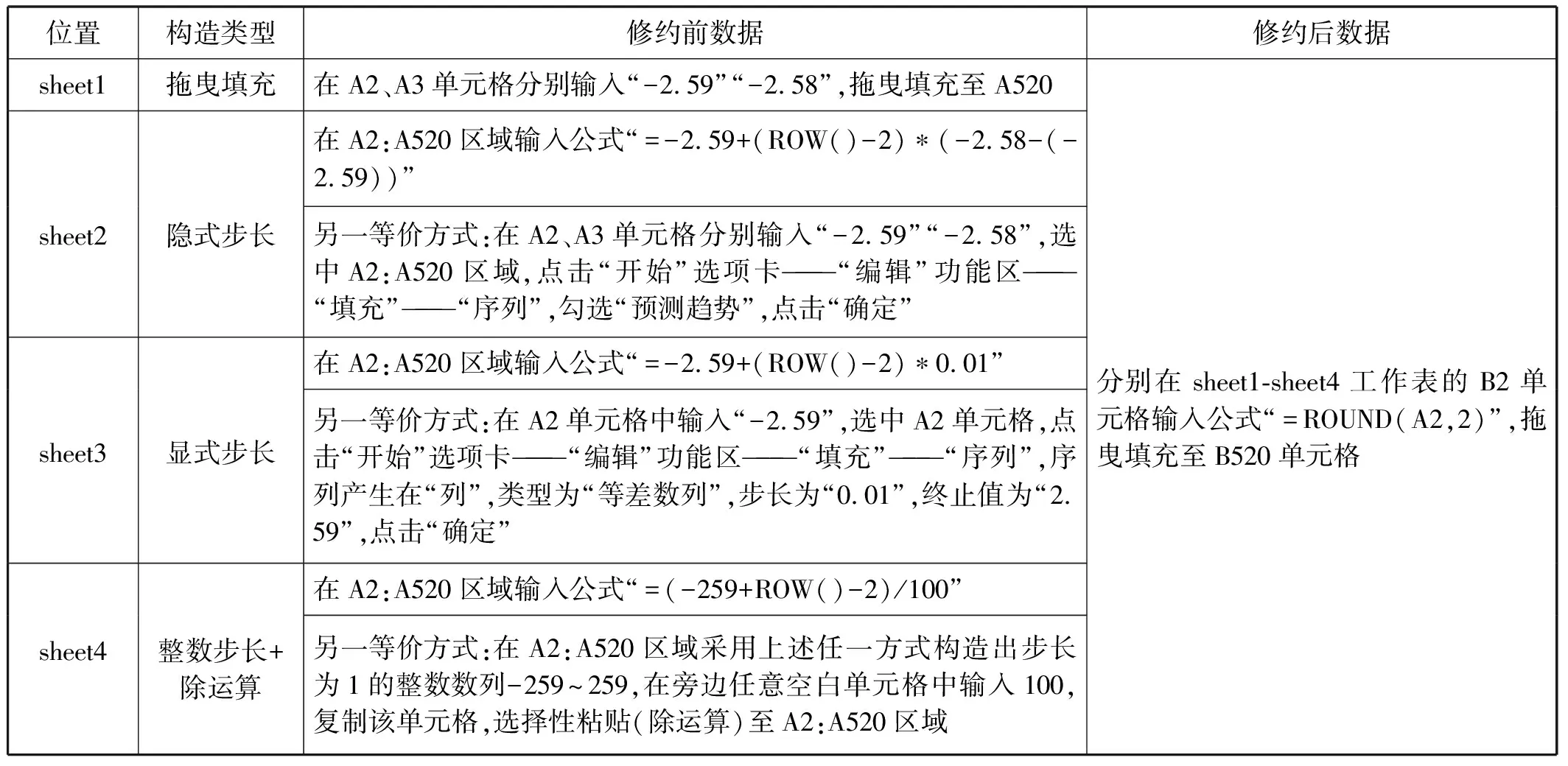
表1 构造小数数列和修约的方式
2 数值查找匹配
2.1 “=”匹配
分别在sheet1-sheet4工作表的C2单元格输入公式“=A2=B2”,拖曳填充至C520单元格。当修约前后数据的数值一致时,该公式结果为“TRUE”(表中以“T”表示),否则为“FALSE”(表中以“F”表示)。
另一等价方式:分别在sheet1-sheet4工作表的C2单元格输入公式“=COUNTIF(A:A,B2)”,拖曳填充至C520。当修约前后数据的数值一致时,该公式结果为“1”,否则为“0”。
2.2 MATCH函数匹配
分别在sheet1-sheet4工作表的D2单元格输入公式“=MATCH(A2,B:B,0)”,拖曳填充至D520。当修约前后数据的数值一致时,该公式结果为该数值所在行的行号(表中以“R”表示),否则为“#N/A”(表中以“N”表示)。
另一等价方式:分别在sheet1-sheet4工作表的D2单元格输入公式“=VLOOKUP(A2,B:B,1,0)”,拖曳填充至D520。当修约前后数据的数值一致时,该公式结果为修约后的数值,否则为“#N/A”。
2.3 数值匹配结果
表2展示了部分代表性的匹配结果。
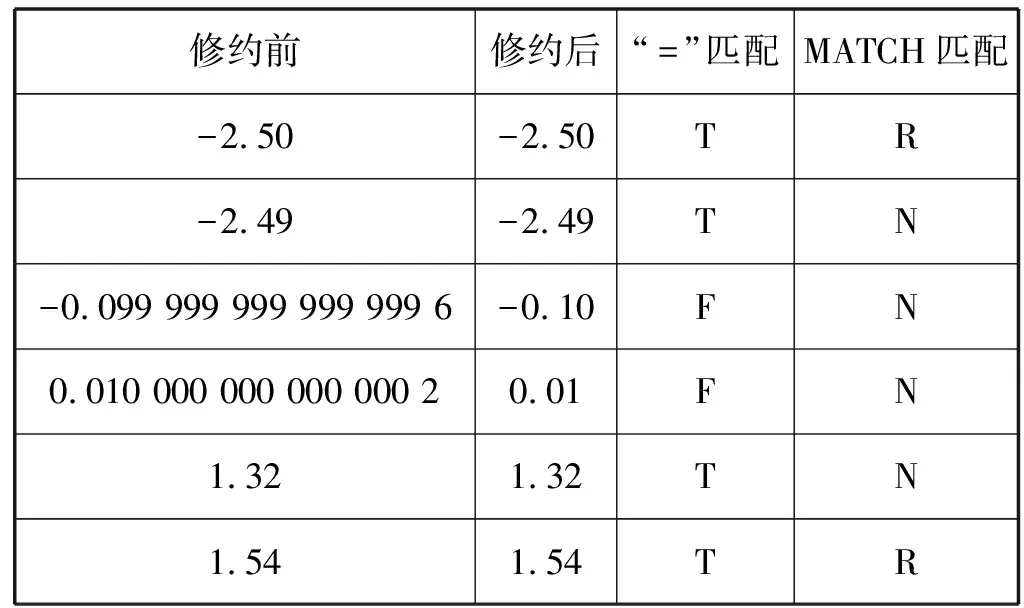
表2 sheet3数值匹配结果示例
表3中匹配结果为“FALSE”或“#N/A”的数目即为修约前后数值不匹配的数据数目。不同构造方式生成的数据,匹配结果也不相同,只有最后一种方式构造生成的数据在修约前后能够完全匹配。
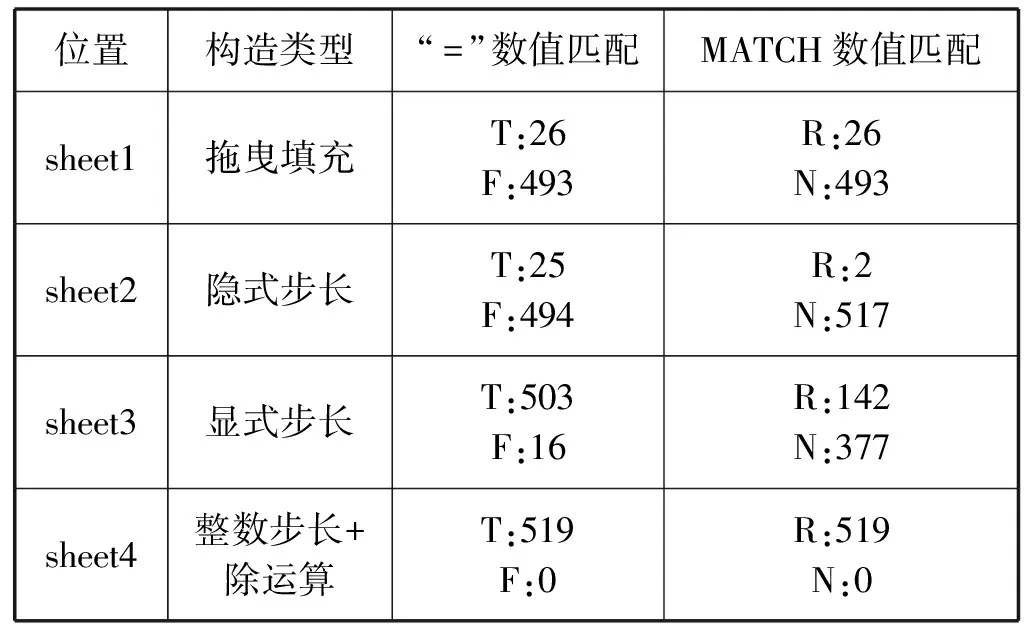
表3 修约前后数据的数值匹配结果
MATCH函数未能匹配的数据在sheet2和sheet3中多于“=”未能匹配的数据。经确认,“=”未能匹配的都是存在可见误差的数据(如表2中通过“显式步长”方式生成的数据“-0.10”实际显示为“-0.099 999 999 999 999 6”)。而MATCH函数未能匹配的数据中,除包含全部存在可见误差的数据外,还有部分数据看上去并无异常。
此外,对sheet1-sheet4中修约后的数据进行交叉匹配,未出现不匹配的结果,说明不同方式生成的数据在修约后都是完全一致的。
计算机中数据的存储和运算都是基于二进制的形式,十进制小数会被转换为二进制浮点数,但是有些十进制小数无法用有限位的二进制数来表示,或者需要非常多位的二进制数来准确表示。但物理存储空间是有限的,软件设计时遵循的标准规范对于数据类型的长度也会有规定,这些都可能造成数据精度的损失。
微软宣称Excel对于浮点数的存储和运算严格遵循IEEE 754标准,双精度浮点数以二进制形式存储在65位范围内(包括1个符号位、11位指数、1个隐含位和52位尾数),精度取决于尾数的大小。尽管存储的数值可以非常大(最大值为1.797 693 134 862 32E+308,最小正数为2.225 073 858 507 2E-308),但是精度最高只有15位有效数字——在引言中已经验证了Excel中的显示精度确实为15位。当精度损失达到这一显示精度(有效数字不超过15位)时,即呈现为可见的误差。
但是这解释不了“=”和MATCH函数匹配结果的不一致。尽管根据种种迹象可以推测这部分异常是由于Excel的存储精度与显示精度不一致导致的,MATCH函数能够识别超出15位显示精度的差异,而“=”只能识别15位的可见精度差异,但是缺乏直接的证据。那么在无法获得Excel源代码的情况下,如何能够获得直接的证据?
3 文本查找匹配
3.1 获取17位精度的数据
Excel工作簿(2007版以上的“.xlsx”文件)本质是一个压缩文件,其中的工作表其实是以“.xml”格式单独存储的。将Excel文件的扩展名由“.xlsx”改为“.zip”或“.rar”,然后使用解压缩软件打开,进入“xlworksheets”目录,即可看到与各工作表名称相同的“.xml”文件,使用网络浏览器(如Internet Explorer、Chrome等)或记事本程序打开“.xml”文件后,即可看到其中的XML代码(图1)。XML代码中,元素

图1 sheet1的XML代码(局部)
将上文中的Excel示例文件另存为副本后按上述步骤操作,分别打开sheet1-sheet4对应的“.xml”文件,从中提取存储的A2:B520区域内所有单元格的数据(此步骤需使用自编程序处理或使用Excel中Power Query查询功能,限于篇幅不再赘述),然后以文本格式(文本格式可保留超过15位有效数字,而数值格式则会丢失15位之后的有效数字)录入至原Excel文件中各自工作表的E2:F520区域,即获得了原本在Excel中不可见的17位精度的数据(E、F列分别为修约前后的A、B列数据的17位精度文本)。
3.2 15位文本“=”匹配
15位文本“=”匹配的目的是模拟15位显示精度下数据的匹配。
为了规避15位显示精度的限制,17位精度的E、F两列数据以文本格式存储,因此无法使用常规的数值修约函数,而是通过下述公式“修约”至15位有效数字后再进行匹配。
分别在sheet1-sheet4工作表的G2单元格输入公式“=IF(LEN(E2)>5,LEFT(E2,LEN(E2)-17+15),E2)=IF(LEN(F2)>5,LEFT(F2,LEN(F2)-17+15),F2)”,拖曳填充至G520单元格。当修约前后数据的文本完全一致时,该公式结果为“TRUE”,否则为“FALSE”。该公式含义如下:(1) 当文本长度大于5位时,通常为17位有效数字,此时文本总长度减去17,得到其中可能包含的负号“-”、小数点“.”、前导“0”所占的位数,再加上15,即为按15位有效数字截取文本;(2) 当文本长度小于5位时,直接取原文本,不进行截取;(3) 用“=”对两处文本进行匹配。
上述公式并不严谨,因为:(1) 按文本截取的规则可能与数值存储和运算时的舍入规则不同,导致误判;(2) 长度超过5位但不足17位的数据、以科学记数法表示的数据,其最终截取的位数有可能不正确;(3) 截取后末尾有多个“0”的数据与未经截取末尾没有“0”的数据无法匹配。但由于此时数据为文本格式,通过Excel公式难以处理上述问题,遇到此类情形时只能进行人工判断(更好的方式是在支持17位精度以上的程序中将其作为数值舍入到15位之后进行比较)。
3.3 全文本“=”匹配
全文本“=”匹配是对具有17位有效数字精度的数据文本进行直接比较。
分别在sheet1-sheet4工作表的H2单元格输入公式“=E2=F2”,拖曳填充至H520单元格。当修约前后数据的文本完全一致时,该公式结果为“TRUE”,否则为“FALSE”。
3.4 文本匹配结果
表4展示了部分代表性的匹配结果。
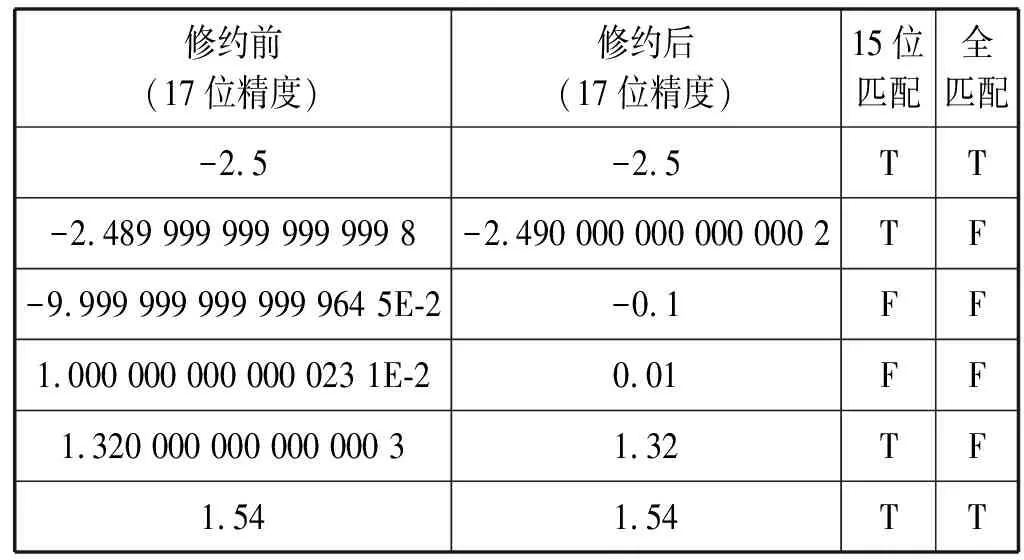
表4 sheet3文本匹配结果示例
表5中,MATCH函数数值匹配的结果与全文本 “=”匹配(17位精度)的结果完全一致,说明MATCH函数能够识别17位有效数字的精度。15位文本“=”匹配的结果与“=”数值匹配的结果完全一致,说明“=”用于数值匹配时只能够识别15位有效数字的精度(“=”用于文本匹配时不存在有效数字精度的问题)。
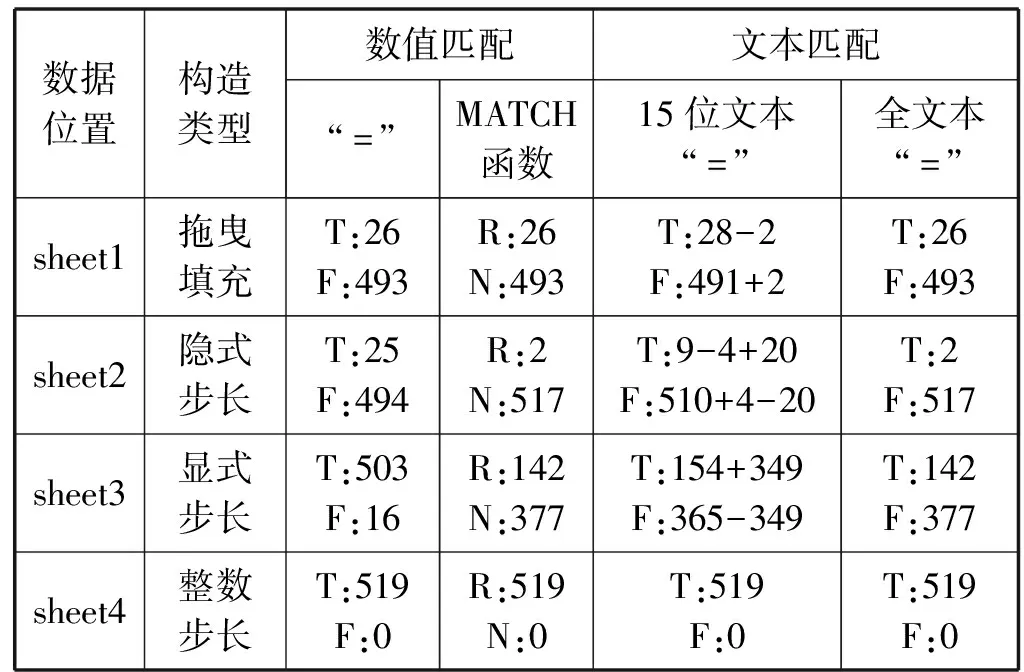
表5 修约前后数据的匹配结果
从“.xml”文件中获取的Excel存储数据可知,在Excel中的显示精度与存储精度确实存在差异,存储精度可达17位有效数字,而显示精度只有15位。Heiser[8]从理论的角度解释了为什么Excel中同时存在这两种精度:IEEE 754标准中还有一种80位扩展双精度浮点数格式,相当于十进制数的17位精度,微软将Excel设计为在寄存器中使用该扩展精度进行运算,以获得更高的中间结果精度,运算后的结果转换为15位精度后返回。
经验证,MATCH、LOOKUP、VLOOKUP、HLOOKUP、RANK、FREQUENCY、DELTA等函数能够识别超过15位有效数字精度的数值,而“=”和COUNTIF等函数则只能识别15位有效数字精度的数值。
4 结果与讨论
本文通过比较Excel界面中显示的数据以及从“.xml”文件获取的内部存储数据,直接证明了如下事实:
(1) Excel中数值的存储精度为17位有效数字,而显示精度为15位有效数字。
(2) 不高于显示精度(不超过15位有效数字)的浮点数误差表现为可见误差。
(3) 高于显示精度(超过15位有效数字)的浮点数误差表现为不可见的误差。
采用不同的构造方式生成了“相同”的小数数列,发现:
(1) 不同的操作方式(填充序列和公式)可能产生完全相同的结果(可见误差与不可见误差均相同),相关数据限于篇幅未体现在文中,读者可根据本文所述方法进行验证。
(2) 相似的操作(“隐式步长”“显式步长”和“整数步长”)可能产生不同的结果(“隐式步长”构造的数据包含更多的可见误差,“显式步长”构造的数据包含更多的不可见误差,而“整数步长”构造的数据则不包含可见误差和不可见误差),甚至如引言中所举的例子,仅仅是运算顺序的差异都可能导致不同的结果。
采用不同的匹配公式将修约前后的数据进行比较,发现:
(1) MATCH、LOOKUP、VLOOKUP、HLOOKUP、RANK、FREQUENCY、DELTA等函数能够识别17位有效数字的存储精度。
(2) “=”和COUNTIF等函数只能识别15位有效数字的显示精度。
4.1 浮点数误差的识别与修正
4.1.1可见误差的识别与修正
可见误差的识别可以使用LEN函数来获取原始数据的长度,当长度超过13位时,则很可能出现了可见误差。
可见误差的修正建议使用ROUND函数。
微软给出的另一种解决方式是设置显示精度:在“文件”选项卡——“选项”——“高级”中勾选“将精度设为所显示的精度”。勾选之后会导致工作簿中所有的数值都将精度调整至所显示的精度,这一操作是不可逆的,强烈不建议采用。
4.1.2不可见误差的识别与修正
不可见误差的识别可以参照本文2.2节使用MATCH等函数对修约前后的数据进行匹配,当返回结果为“#N/A”时,则表明出现了不可见误差。
对于不可见误差的修正,除了使用ROUND函数或设置为显示精度的方式外,笔者在研究中还发现了另一种有趣的方式:(1) 将sheet3中A列的数据复制并选择性粘贴为值;(2) 任意选取“=”匹配结果为“TRUE”、MATCH函数匹配结果为“#N/A”的数据(即存在不可见误差的数据),如A12单元格的“-2.49”,双击该单元格进入编辑状态,直接按Enter键,此时MATCH函数匹配结果将由“#N/A”变为“12”,说明不可见误差被修正了。
通过以下方式可以修正整列数据的不可见误差:选中A列,点击“数据”选项卡——“数据工具”功能区——“分列”,直接点击“完成”。此时MATCH函数匹配结果中#N/A的数目将从最初的377个缩减至16个(这16个均为存在可见误差的数据)。
上述修正方式仅对静态数据有效,因为公式的结果是会重新计算的(“.xml”文件中同时储存了公式和计算结果)。
笔者推测其原理如下:原本显示的数值是经过某些运算或操作得到的,与直接输入的数据存在微小差异原数据为“-2.489 999 999 999 999 8”,修正后的数据为“-2.490 000 000 000 000 2”,与修约后的数据相同),修正的过程相当于按照15位显示精度进行了修约,舍弃了15位之后的尾数,因而与ROUND函数修约的结果一致(误差只出现在15位有效数字之后,因此,在本例中修约至15位有效数字之前都将得到相同的结果)。
4.2 目前无法解决的问题
仍然有一些与浮点数误差相关的问题是目前无法解决的,例如:
(1) 无法再在单元格中输入“39 524.848”,结果会显示为“39 524.847 999 999 9”。
(2) 无法进行超出15位有效数字的运算,“=1+0.000 123 456 789 012 345”的结果为“1.000 123 456 789 01”。
这些问题只有留待相关理论与标准规范的进一步发展,比如提升数据精度以减少此类问题的出现概率,或是发明更先进的存储和运算方式,无损地进行十进制与二进制的转换,从而在根本上解决此类问题。
5 结 语
Excel的易用性是一把双刃剑,一方面使得不具备编程能力的用户也可以在Excel电子表格环境中进行简单的“编程”——通过组合使用Excel内置函数以实现特定的功能;同时也使得原本应当由程序员处理的浮点数误差变成了普通用户需要面对和解决的问题[9]。
Excel中淡化了数据类型的概念,但是对于整数和小数的操作仍然是有区别的,这一区别源自部分十进制小数转换为二进制时不可避免的精度损失。因此进行涉及小数的比较与查找等操作时,务必非常谨慎。使用ROUND函数修约应当成为习惯,这是规避此类问题最有效的手段。需要指出的是,修约并没有避免精度损失(如表4中修约后的“-2.49”在17位精度下为“-2.490 000 000 000 000 2”,仍然存在误差),而是通过主动损失精度,将可能存在误差的部分尾数舍弃,只保留真正关注的“主体”数据。
