基于PCNN与混合加权的多波束声呐图像镶嵌方法

曲 萌,高兴国,王 峰,闫循鹏,阳凡林,3

(1.山东电力工程咨询院有限公司,山东 济南 250013; 2.山东科技大学 测绘与空间信息学院,山东 青岛 266590;3.自然资源部 海洋测绘重点实验室,山东 青岛 266590)

多波束测深系统(multibeam echosounder system,MBES)能够获取海底的反向散射强度(backscatter,BS),利用反向散射强度可以生成声呐图像并用于海底底质分类与海底目标识别[1-2]。受测量中海洋环境和仪器自身误差的影响,原始数据存在明显的系统性误差[3]。经过传播损失改正、角度响应改正等处理后,声强数据中的系统性误差明显减小[4]。但由于改正不完善,在条带间仍存在由残差引起的声强差异,表现在声呐图像上为重叠区域明显的拼接线,对海底底质分类与目标识别造成干扰,影响图像质量和应用。此外,由于测量时声波入射角不同,重叠区域在不同条带声呐图像中呈现不同的纹理特征。因此,在应用声呐图像之前,需对声呐图像进行镶嵌以消除重叠区域差异,并尽量保留更多细节信息,对提高声呐图像质量具有重要意义。

声呐图像处理需进行图像配准和图像镶嵌。图像配准的主要目的是消除图像的几何畸变。多波束测深系统通常采用“平均声强法”对回波序列进行采样,得到的声强点与测深点一一对应,经过波束归位后,采样点具有较高的几何精度,可认为不存在几何畸变。图像镶嵌的主要目的是消除图像灰度畸变,实现多图像的无缝拼接。在光学图像拼接中,常采用的方法有平均法、混合加权法(blending weighted fusion,BWF)[5]、泊松法[6]等。其中,混合加权法由于计算简便、效率高等优势,在图像拼接中应用广泛。目前,对于多波束声呐图像相邻条带的拼接研究相对较少。孙文川等[7]提出一种基于加权最小二乘估计的声强数据归一化方法,以消除重叠区域与非重叠区域的强度差异。赵建虎等[8]提出一种通过滑动窗口逐ping确定拼接线的拼接方法,但该方法需要进行相邻条带ping的匹配。朱正任等[9]提出一种基于多条带最小二乘拟合的多波束声呐图像残差处理方法,有效削弱了残差对声呐图像的影响。上述方法主要针对相邻条带拼接线的消除问题,在一定程度上削弱了条带间声强的残差,但未顾及重叠区域纹理信息存在的差异,易造成信息损失。在光学图像处理中,常基于图像融合实现信息的综合,并以多尺度变换作为图像融合框架,如离散小波变换、非下采样轮廓波变换、非下采样剪切波变换(non-subsampled shearlet transform,NSST)等。在变换域内,对不同尺度的图像分量按照不同的规则进行融合,可以得到比较理想的效果。巩稼民等[10]在NSST域内结合脉冲皮质模型(spiking cortical model,SCM)与引导滤波实现了红外图像与可见光图像的融合。曹义亲等[11]提出一种基于NSST的脉冲耦合神经网络与稀疏表示相结合的多元遥感卫星图像融合方法。在声呐图像中,相关研究主要是多波束声呐图像与侧扫声呐图像在小区域的信息综合与互补[12-13],并未考虑声呐图像拼接对图像信息综合的影响。

综上所述,目前多波束声呐图像镶嵌方法未能实现大区域无缝拼接和信息综合的有效统一。为实现多波束声呐图像的无缝拼接,同时顾及重叠区域纹理差异,实现图像信息综合,本研究基于脉冲耦合神经网络(pulse coupled neural network,PCNN)和混合加权法,在NSST变换域内进行多波束声呐图像的镶嵌,消除图像中存在的灰度畸变,实现声呐图像的拼接和信息综合。

1 NSST域内多波束声呐图像镶嵌方法

针对多波束声呐图像镶嵌问题,为了实现相邻条带的无缝拼接,本研究提出一种在NSST域内结合PCNN与混合加权的多波束声呐图像镶嵌方法(如图1)。首先对多波束反向散射强度数据进行传播损失、角度响应等系统误差的改正,再按照地理坐标对两条带图像进行配准。多波束声呐图像镶嵌过程在NSST的基础上进行,主要步骤包括源图像NSST变换、低频图像融合、高频图像融合与NSST逆变换。其中,低频图像融合采用混合加权方法,以削弱图像间的拼接线。高频图像融合采用PCNN,充分保留图像的细节纹理信息。最后通过NSST逆变换完成多波束声呐图像的镶嵌。

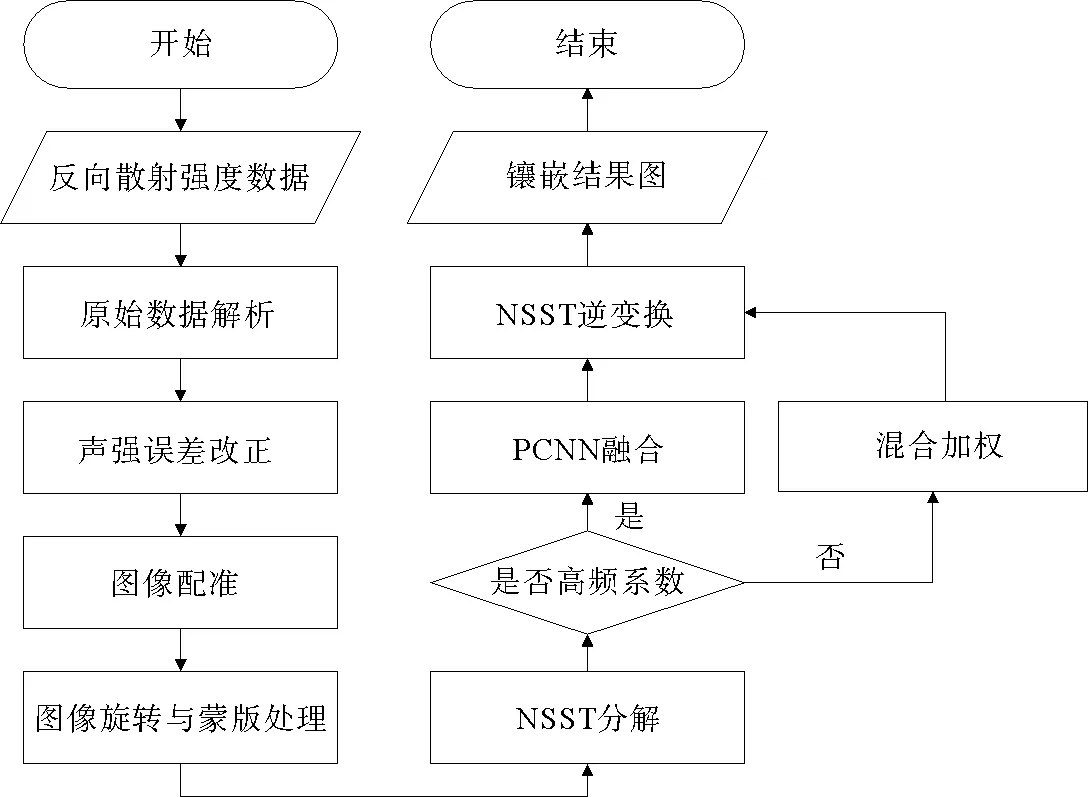
图1 多波束声呐图像镶嵌流程图

1.1 NSST图像变换

图2展示了图像NSST变换的过程,主要包括多尺度分解和方向局部化。图中的方框表示频域图像。首先使用上采样得到的非下采样金字塔(non-subsampled pyramid,NSP)滤波器组对频域图像进行多尺度分解,得到一个低频和一个高频子带系数[14],对低频子带可继续进行分解得到更小尺度的低频和高频系数。然后对所有高频子带进行方向局部化,方向局部化采用剪切波滤波器(shearlet filter,SF)。在频域内将剪切波滤波器窗口作用于分解得到的高频子带,获得不同方向子带[15]。如图2所示,经过NSST变换后得到一个低频子带系数和若干不同方向的高频子带系数。NSST可以避免图像的下采样操作,同时避免了伪吉布斯现象,具有良好的平移不变性。

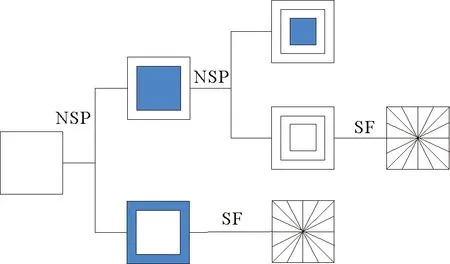
图2 非下采样剪切波变换(NSST)过程示意图

1.2 低频系数的混合加权融合

低频系数包含纹理、结构等信息,能够反映声呐图像之间的强度差异。为了削弱图像中存在的灰度畸变,同时充分保留低频系数的有效信息,实现条带间的无缝拼接,采用混合加权法对低频系数进行拼接。混合加权法是根据重叠区域的宽度,以每个像素点到重叠区边界的距离进行定权,使得图像在重叠区边界平滑过渡,削弱声强差异,表达式为[5]:

(1)

式中:Il和Ir分别表示左图像与右图像;x和y分别表示像素点在图像坐标系中的坐标;W1和W2是两条带重叠区域像素点(x,y)的权重函数,且W1+W2=1。权重函数为:

(2)

式中,Xl和Xr分别表示重叠区域的左边界和右边界坐标。

1.3 高频系数的PCNN融合

高频系数反映图像的突变特性,含有丰富的细节信息。本研究将PCNN方法引入多波束声呐图像镶嵌领域,通过PCNN点火次数可有效获取图像的纹理等细节信息,实现多波束声呐图像的细节信息综合。PCNN是由若干神经元组成的单层二维神经网络,每一个神经元都与图像中的一个像素点对应。单个神经元由接收域、调制域和脉冲发生器三部分组成[16],如图3所示。其中,F为反馈输入,L为连接输入,U为内部活动项,Y为输出部分,W为权阵,β为连接强度,E为活动阈值。

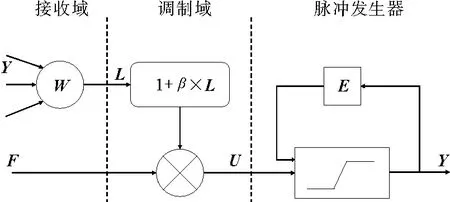
图3 脉冲耦合神经元结构

传统的PCNN模型存在参数众多、迭代计算较慢等缺陷,因此衍生了较多简化的PCNN模型。其中,SPCNN(simplified PCNN)是由Chen等[17]在SCM基础上提出的,并提供了参数的自动设置方法,SPCNN模型的迭代过程为:

Fij(n)=Sij,

(3)

(4)

Uij(n)=e-αFUij(n-1)+Fij(n)(1+βLij(n))。

(5)

(6)

Eij(n)=e-αEEij(n-1)+VEYij(n)。

(7)

式中:Fij表示反馈输入项,Lij表示连接输入,Uij表示内部活动项,Yij表示脉冲输出,Eij表示动态阈值,n为迭代次数,下标i、j、k、l均表示像素坐标位置,VL和VE分别为连接输入和动态阈值的幅值,αF和αE分别为反馈输入和动态阈值的时间衰减常数。

式(3)将外部激励Sij作为反馈输入。式(5)为脉冲调制部分,通过将反馈输入和连接输入进行耦合,得到内部活动项Uij,由于神经元的漏电积分特性,调制项Uij随着每次迭代按照αF进行指数衰减。将Uij和Eij进行比较,当Uij大于阈值时,该神经元点火,即Yij=1;否则神经元不点火,Yij=0,得到的二维图Y称为点火图。如果神经元点火,动态阈值按VE跃升,如果不点火,则按照αE进行指数衰减[16]。

SPCNN模型中的5个参数分别是VL、αF、β、VE、αE,均可进行自适应计算,如表1所示。其中,σ(I)表示图像的标准差,Smax和S′分别表示最大像素值和归一化Otsu阈值,其余参数同SPCNN模型一致。

表1 SPCNN参数自动设置[17]

连接强度β是SPCNN模型中一个重要的参数,反映了各神经元模型之间的连接强度,表征了某一神经元受其邻近神经元的影响大小[17]。传统PCNN算法中,所有神经元均采用相同的连接强度,未考虑不同像素点的贡献差异。实验采用改进的拉普拉斯能量ML和拉普拉斯能量SML定义连接强度[18]:

ML(i,j)=|2I(i,j)-I(i-1,j)-I(i+1,j)|+|2I(i,j)-I(i,j-1)-I(i,j+1)|,

(8)

(9)

式中:i和j表示像素坐标,I为高频子带系数,拉普拉斯算子步长设置为1,ML值累加窗口大小为3×3。

权阵W按照欧式距离倒数进行计算:

(10)

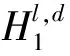
Tl,d(n)=Tl,d(n-1)+Yl,d(n)。

(11)

式中:Yl,d(n)表示l层d方向的第n次点火次数;Tl,d(n)表示l层d方向的前n次迭代累计点火次数,即该像素点在迭代计算过程中被激发的总次数。以点火次数作为判决算子,按照点火次数的大小进行融合:

(12)

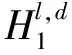
1.4 NSST逆变换

经过低频信息融合和高频信息融合后,实现了两图像的信息综合,消除了低频信息中的拼接线并保留高频特征信息。最后将两幅图像融合后的低频系数L和一系列高频系数Hl,d进行NSST逆变换,得到两幅图像镶嵌后的结果。

2 实验与分析

2.1 实验数据

本研究采用多波束测深系统实测数据进行声呐图像镶嵌实验。实验数据采集于2011年3月8日,来源于2012年浅水调查会议资料[19]。调查区域位于新西兰惠灵顿附近海域,平均水深约20 m(图4),图4(b)中X、Y表示高斯投影后的平面坐标。使用Kongsberg EM2040多波束测深系统以平均声强方式获取的实验数据进行验证。多波束测深系统的工作频率为300 kHz,波束宽度为1°×1°,波束开角为120°,采样模式为等距采样。

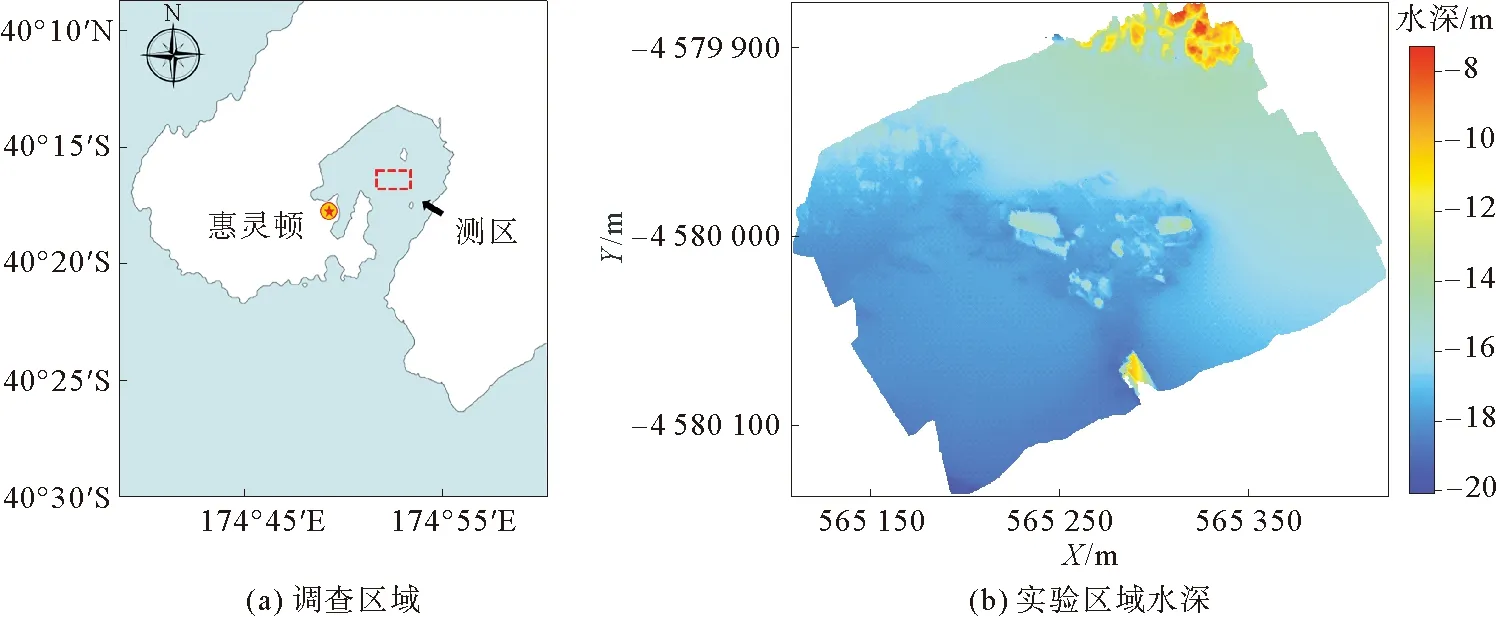
图4 实验区域概况

2.2 评价指标

为准确、客观地评价信息综合效果,选择信息熵、标准差、空间频率用于定量分析,从不同角度反映信息综合效果。上述指标值越大,表明图像的质量越高。

信息熵作为一种图像质量评价指标,常被用来衡量图像中包含信息的丰富程度。信息熵越大,图像包含的信息量越多,计算公式为:

(13)

式中:IE表示信息熵,L表示待测图像像素灰度最大值,Pk表示像素值为k的像素个数。

标准差通过对图像进行统计,得到像素的离散程度。标准差越大,图像的灰度值离散程度越高,视觉效果越好,计算公式为:

(14)

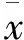
空间频率是基于梯度的图像质量指数,能够有效衡量图像的梯度分布,用来估计图像的纹理和细节[20]。SF越大,表明图像具有丰富的边缘和纹理,计算公式为[20]:

(15)

其中:

(16)

式中:RF与CF分别表示图像的空间列频率与行频率,M和N表示图像的行列数。

2.3 实验结果与分析

为验证本研究方法的有效性,对调查区域的7个条带数据进行镶嵌实验。首先对数据进行预处理,主要包括:①对原始多波束反向散射强度进行解析,并结合导航、姿态等辅助数据对各条带进行波束归位,将各条带数据纳入统一的坐标框架下;②对各条带数据进行传播损失、入射角效应和中央异常改正等各项声强误差处理,以削弱系统误差的影响;③对图像进行旋转,使得航迹线方向大致与图像纵轴平行,利用图像蒙版操作提取相邻条带重叠区域,完成预处理。再使用本研究方法对各条带进行镶嵌,主要过程为:①首先对各条带重叠区域图像进行NSST分解,分解层数设置为2,各层方向数设置为16,得到高低频子带图像;②对低频子带图像,沿着图像横轴方向,按照混合加权法进行拼接;③对高频子带图像,按照PCNN进行融合,迭代次数为200,其余参数按照表1进行计算。对该调查区域的7个条带数据进行镶嵌,镶嵌前后的结果如图5所示。

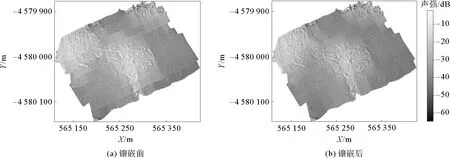
图5 实验区多波束声呐图像镶嵌结果

从图5(a)中可以看出,尽管经过误差改正处理,条带间仍存在系统性残差,表现为明显的拼接线,该现象影响声呐图像的进一步使用。经本研究方法镶嵌后,如图5(b)所示,能有效削弱图像的灰度畸变,无明显拼接痕迹,且底质和纹理特征的边界清晰,能够较好地保留图像的纹理信息,实现多条带的无缝拼接。

为了说明本研究方法的有效性,选取实验区域内具有代表性的相邻两条带进行分析,两条带重叠区域大、强度差异明显。采用平均法、混合加权法和本研究方法分别对条带重叠区域图像进行镶嵌处理,实验结果如图6所示。

图6 多波束声呐图像镶嵌效果对比

从图6(a)可以看出,原始数据存在的残差造成了重叠区域边界明显的拼接线。图6(b)中,经平均法镶嵌后,两条带总体声强较一致。但由于只对重叠区域数据进行平均化,削弱了部分随机噪声,导致重叠区域更加平滑,与非重叠区域间的纹理细节存在一定差异,因此镶嵌结果仍存在较明显的拼接线。图6(c)中,混合加权法总体上效果较好,条带间声强过渡均匀,无明显的拼接线。但在加权计算过程中,损失了地物地貌的细节信息,使图像存在一定程度的模糊。图6(d)中,本研究方法在低频系数上利用混合加权法消除了拼接线,并对高频系数进行信息提取,保留了细节信息,有效实现了多波束声呐图像的镶嵌。下面分别从拼接效果和信息综合效果两方面分析本研究方法的有效性。

1) 拼接效果分析

为了定量评价本研究方法在消除条带间拼接线方面的有效性,首先在声呐图像镶嵌结果图(图6)中沿垂直航迹线方向取一横向截面(黄色直线),该截面跨越了相邻条带的拼接线且底质类型基本一致;然后分别计算拼接线两侧一定范围内声强的统计特征,如表2所示。

表2 拼接线两侧声强统计特征

图7显示了截面处不同镶嵌方法的拼接效果。红色实线与黄色实线分别表示拼接线两侧的声强均值。在图7(a)中,原始图像条带之间在重叠区域存在明显的声强差异,约为-6.18 dB。在图7(b)平均法处理结果中,拼接线两侧均值相差2.81 dB,条带边界处呈明显的阶梯状。此外,如表2所示,平均法处理结果中拼接线两侧的声强标准差相差0.1 dB,表明重叠区经过平均化处理后,削弱了随机噪声影响,与非重叠区域存在一定差异。因此,在镶嵌结果图6(b)中有较明显的拼接痕迹。在图7(c)混合加权方法中,拼接线两侧均值相差1.15 dB,比平均法降低了59%,表明该方法能够有效削弱拼接线两侧声强差异,实现声强的均匀过渡。该方法拼接线两侧声强标准差相差0.15 dB,说明加权处理削弱了随机噪声的影响。在图7(d)本研究方法中,拼接线两侧声强均值相差1.29 dB,总体上无明显阶跃,表明对NSST分解后的低频系数进行混合加权处理能实现声强的无缝拼接。此外,如表2所示,本研究方法拼接线两侧声强标准差基本一致,表明对NSST分解后的高频系数进行PCNN融合能保持声呐图像的原始细节信息,避免加权处理弱化图像的纹理信息。

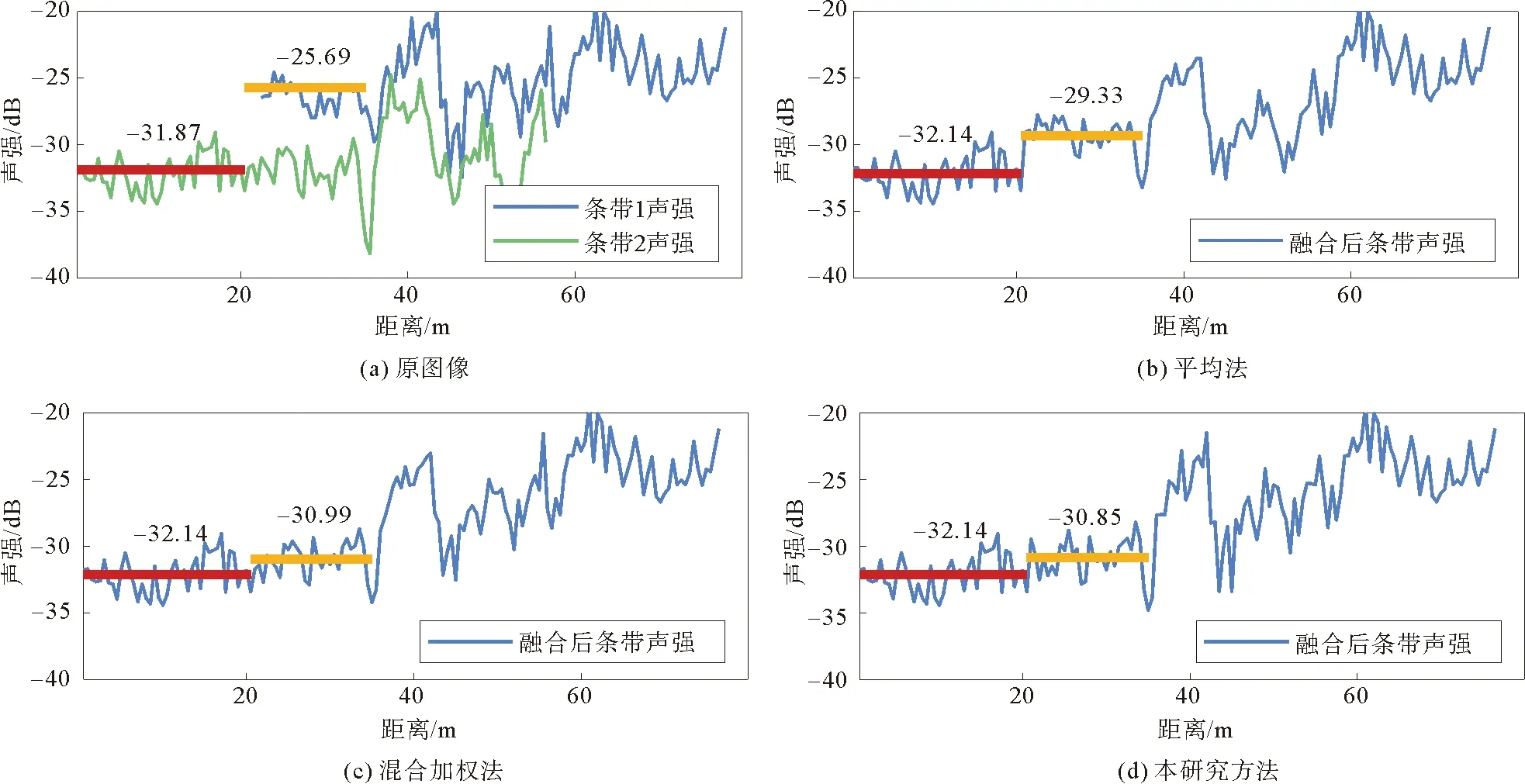
图7 拼接线两侧声强比较

2) 信息综合效果分析

通过对声呐图像进行镶嵌,实现了相邻条带重叠区域的信息融合。为定量评价3种方法在信息综合方面的有效性,对图像的信息熵IE、标准差SD和空间频率SF进行计算,结果如表3所示。

表3 声呐图像信息综合效果评价

从表3可以看出,3种镶嵌方法的标准差相近,本研究方法实验结果标准差稍高,与平均法和混合加权法相比,分别提升0.8%和0.9%。本研究方法实验结果的信息熵最高(3.25),平均法次之,混合加权法最低。主要原因是混合加权法在计算过程中未考虑具体区域的纹理信息,仅按照像素点位置加权,可能会损失部分纹理信息。与其他两种方法相比,本研究方法的信息熵分别提升2.5%和4.2%,表明该方法在保持信息丰富程度上具有一定优势。本研究方法的空间频率为22.76,分别比平均法的18.84、混合加权法的17.29提升了20.8%和31.6%,表明镶嵌结果图中具有丰富的边缘信息,图像质量更高。

从图6中的源图像和拼接后声呐图像中提取子区域(黑色矩形),如图8所示。从图8(a)和8(b)中可以看出,条带之间的纹理信息差异明显,不同条带的重叠区域的细节信息不同,且呈较强的互补性。主要原因是采用多波束声呐测量同一区域时,不同条带的波束入射角和方位角不同,导致返回的信号存在差异。经过镶嵌处理后,平均法(图8(c))和混合加权法(图8(d))的镶嵌结果均存在一定的模糊。本研究方法的镶嵌结果(图8(e))纹理特征明显、边界清晰,能够保持更丰富的细节信息。

图8 声呐图像镶嵌信息综合结果

3 结论

本研究针对多波束声呐图像镶嵌中存在的拼接线消除与信息综合问题,提出一种在NSST域内结合PCNN和混合加权法的图像镶嵌方法,并利用实测多波束海底反向散射强度数据进行实验分析。实验结果表明,本研究方法能够有效削弱条带间的拼接线并消除灰度畸变,同时能够保留较为全面的纹理细节信息,可为声呐图像的镶嵌任务提供参考。但当重叠区域较窄、海底底质较为单一且无明显纹理特征时,该方法存在一定局限性,需要进一步研究。