一种顾及随机误差的地面三维激光扫描仪自检校方法

李 霜,樊 亚,付 贵,周腾飞

(1.安徽理工大学 空间信息与测绘工程学院,安徽 淮南 232001;2.中国建筑材料工业地质勘查中心 贵州总队,贵州 贵阳 551400;3.贵州建设职业技术学院,贵州 贵阳 551400;4.同济大学 测绘与地理信息学院,上海 200092)

随着地面三维激光扫描仪(terrestrial laser scanner,TLS)测量技术的发展,点云数据成为三维测量和建模的重要来源。然而,由于系统误差的存在,点云数据可能无法完全反映目标物的真实特征,从而影响测量结果的精度和质量[1]。因此,为保证测量质量和结果的可靠性,必须了解随机误差和系统误差对点云数据的影响,并采取相应的消除方法。传统检校方法[2]的数学模型虽然简单,但不能同时解算多种观测值的系统误差,且需要严格的实验条件和较高的成本。近年来,自检校方法受到越来越多的关注,其本质是将所有检校参数(calibration parameters,Cps)与其他未知参数一起纳入某个函数模型中进行解算[3]。

目前TLS自检校研究主要包含以下3类:①识别系统误差来源方面,现有的研究大多参考全站仪测距误差和轴系误差制定TLS的Cps[4]。由于TLS与全站仪结构不完全相同,此措施在理论上不严密,一些学者试图从扫描仪构造和观测原理出发探究误差的来源[5-6];②自检校模型构建方面,一般基于刚体坐标转换模型实现[7],例如,官云兰等[8]基于Gauss-Markov模型构建了一个具有11个参数的扫描仪自检校误差模型;Reshetyuk[9]将所有参数视为观测值,通过附有参数的条件平差实现了检校参数的求解。尽管自检校法在平差过程中可同时估计Cps和转换参数,但不可避免地导致参数间的高度相关性[10];③影响因素方面,部分学者对粗差[11]、扫描目标分布[12]、目标中心点不确定性[13]与温度[14]对于自检校结果的影响进行了分析。以上研究对系统误差的影响因素和解算方法等进行讨论,为选择适当的自检校方法和参数提供了参考,然而当前的自检校函数模型往往忽略了点云数据的随机误差,理论上不够严格,或者缺乏随机误差对检校结果影响程度的合理评定。

本研究基于Gauss-Helmert模型和TLS观测原理,提出一种顾及随机误差的三维激光扫描仪非线性自检校方法,并联合方差分量估计理论(variance component estimation,VCE)[15]实现不同种类观测值(距离与角度)的后验估计,旨在分析和量化观测值随机误差对TLS自检校未知参数解算和坐标改正的影响。

1 顾及随机误差的自检校方法

常规自检校函数模型未考虑观测值的随机误差,鉴于此,本研究基于TLS观测方程,提出一种新的基子点的TLS自检校方法;同时,采用Newton-Gauss法对函数模型进行线性化处理。

1.1 TLS观测原理

在扫描过程中,TLS以其几何中心为原点,构建独立的空间极坐标系,利用飞行时间理论(time of flight,TOF)测得仪器中心与目标点P之间的斜距s,同时通过角度编码器记录激光线在极坐标系中的垂直角θ和水平角α。遵循球坐标系与笛卡尔坐标系的空间几何关系,以左手系为例,扫描仪观测原理如图1所示。其中:O为坐标系原点;X、Y、Z轴分别表示扫描仪的瞄准轴、水平轴与垂直轴;(x,y,z)表示目标点的三维笛卡尔坐标;(s,θ,α)表示极坐标系下目标点的原始观测值。

脉冲式TLS依托光电测距原理进行测量,距离观测值一般包括加常数m与乘常数λ的系统误差。另外,参考全站仪的轴系误差[8],角度观测值的系统误差项通常包括瞄准轴误差c、水平轴误差i及垂直轴误差t。因此,点云数据的原始观测值与真值往往存在一定偏差,需要进行相应的改正。值得一提的是,相位式扫描仪与脉冲式扫描仪的测量原理不尽相同,两者的系统误差项可能并不等价,使得自检校函数模型的形式存在一定差异,但这对于自检校理论没有直接影响。基于以上5个Cps,顾及系统误差项的TLS观测方程可表示为:

(1)

式中,c′与i′分别为瞄准轴误差与水平轴误差对于水平角观测值的改正。

(2)

1.2 TLS自检校模型

基于点的自检校法通常会利用待检校扫描仪和高精度全站仪对预先设定的目标进行观测。为了保证参考坐标的精度,高精度全站仪的目标物一般选取平面靶标或靶球[16]。在获得目标点的两套坐标数据后,需要将点云数据的三维坐标转换为原始观测值,根据坐标转换模型实现系统误差项的求解。常规自检校函数模型可表示为:

(3)

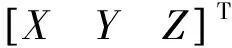
(4)

式中,φ、ω、κ为3个旋转参数。

观察式(3)不难发现,模型没有考虑观测值的随机误差,在一定程度上特别是观测数据精度较低时易导致模型的不稳定。鉴于此,基于Gauss-Helmert模型和扫描仪观测原理,提出一种新的基于点的TLS自检校方法,函数模型为:

(5)

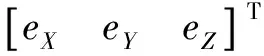
相应地,未知参数可表示为:

(6)

由于常规自检校过程并没有考虑到目标点观测值的随机特征,此时权阵应为单位阵。根据式(5)中不同坐标系下目标观测值的属性,假设全站仪和扫描仪的测量中误差分别为(σX,σY,σZ)和(σs,σθ,σα),且随机误差服从正态分布,则随机模型可表示为:

(7)

此处扫描仪及全站仪的先验信息可根据仪器的标称精度及误差传播定律获得。

1.3 自检校函数模型的线性化推导

由于函数模型采用完整的旋转矩阵R且点云坐标采用原始观测值表示,故因变量与自变量间不能表示为线性对应关系,即提出的自检校法实质上为非线性模型。鉴于此,本研究基于Newton-Gauss法[17]对函数模型进行线性化以实现未知参数的迭代计算。

为便于理解及简化推导过程,首先令:

(8)

设第j次迭代计算后获得的参数估计值为:

(9)

(10)

式中,dT、dφ、dω、dκ、dm、dλ、dc、di、dt为各未知参数的改正数。

(11)

再令

(12)

此时,系统误差项改正数的系数矩阵元素为:

(13)

结合式(11)～(13),对式(10)整理后可得:

(14)

(15)

Aj、Bj分别为第j次迭代时扫描仪观测值随机误差及未知参数改正数的系数矩阵,且有:

(16)

(17)

式中,I3×3表示维度为3的单位阵。

为实现参数的解算,采用式(14)构建加权整体最小二乘问题的拉格朗日目标函数Φ:

(18)

式中:K为拉格朗日乘子,P1、P2分别表示e1、e2的权阵。

令

(19)

根据拉格朗日必要条件,对各变量求导,并令导数为0,即:

(20)

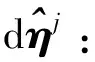
(21)

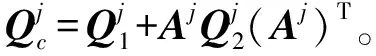
(22)

值得注意的是,观测值的随机误差在迭代过程中需要不断更新[18],且参数向量在第j+1次迭代时的预测值为:

(23)

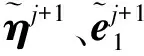
(24)

另外,为提高迭代效率并避免收敛失败,在迭代开始前应确定各变量的初始值。假定仪器在观测时处于理想状态,系统误差和随机误差的初值可设定为零;平移参数和旋转参数的初值可利用线性Bursa-Wolf模型或采用重心化后的坐标获得[8]。

2 算例分析

为分析观测值随机误差对于自检校结果的影响,实验基于仿真数据和实测数据进行,其中仿真数据由真实仪器参数生成,以保证算法的普适性。实验方案设计如下:

方案1文献[8]提出的基于Gauss-Markov模型的自检校法;

方案2仅考虑扫描仪观测值随机误差的自检校法;

方案3本研究提出的基于Gauss-Helmert模型的自检校法;

方案4利用仿真的系统误差真值对观测值进行改正的自检校法。

2.1 仿真数据实验

由于均匀分布的观测目标易导致参数间的高相关性[19],根据TLS真实视场,假设空间中随机分布60个目标点,其中选取50个作为公共点,其余视为检核点。根据真实的检校实验,设定扫描仪几何中心至目标物的距离为5～30 m,垂直角范围为-45°～90°,水平角范围为0～360°;未知参数的真实值与原始观测值中误差如表1所示。假定扫描仪的水平角与垂直角具有相同的先验信息,在仿真过程中按照零均值和给定的单位中误差生成相应的随机误差,仿真1 000次。

表1 原始观测值中误差与未知参数的真实值

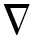
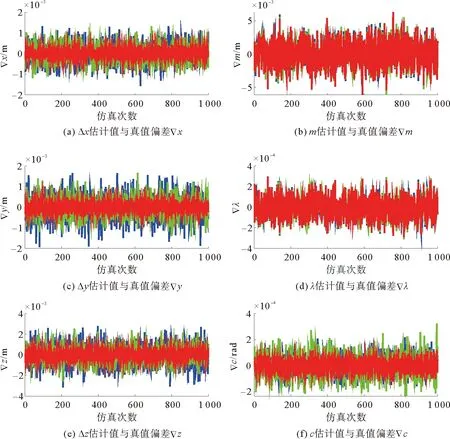
图2 参数偏差与均方根误差

为比较参数估计值与真值对坐标改正的成效,在计算坐标分量误差及点位中误差时利用系统误差的真值对观测值进行改正(方案4),并与以上3种方案进行比较,结果如图3所示.

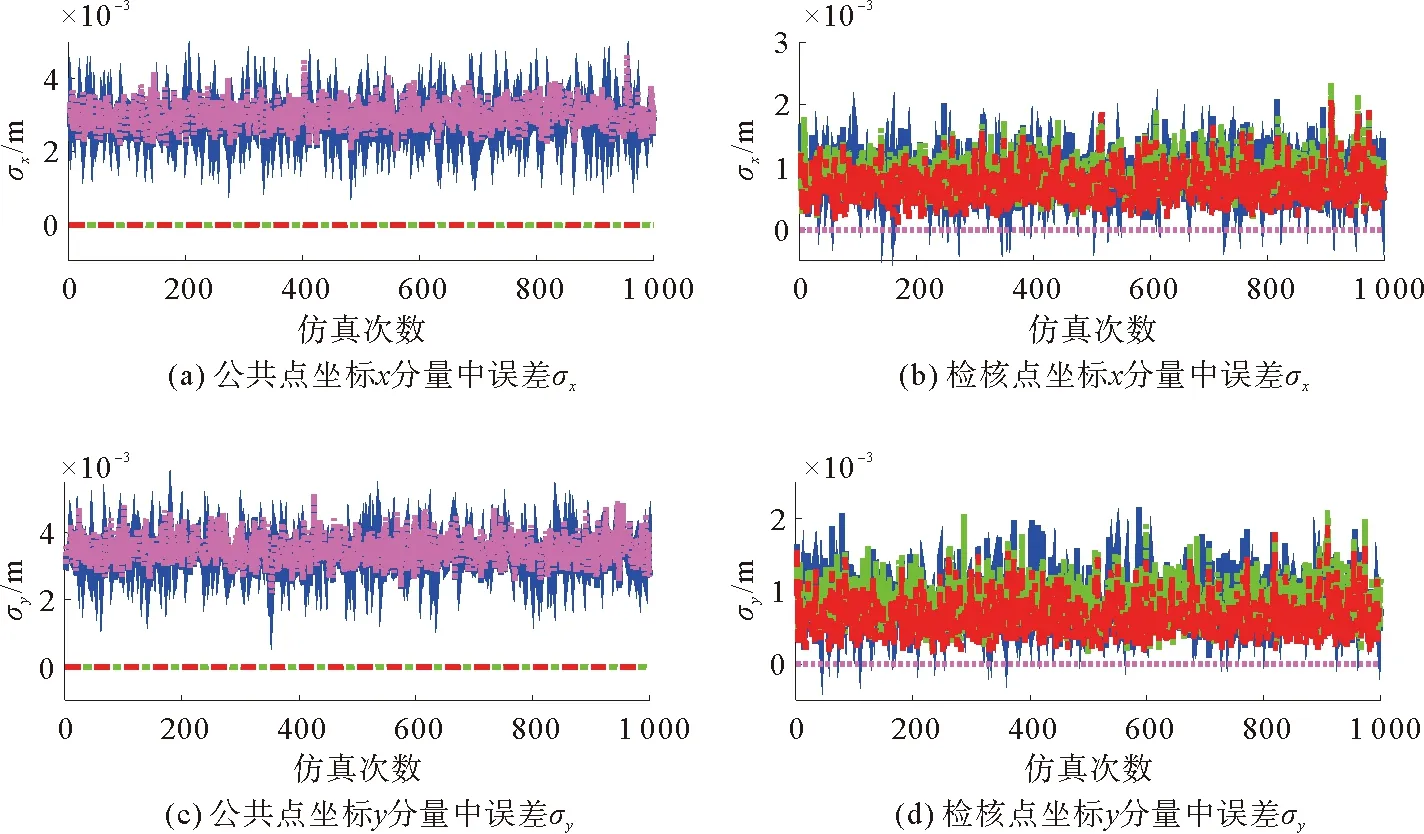
图3 坐标分量误差及点位中误差

2.2 实测数据实验

采用文献[8]给出的实测坐标序列进行实验,数据通过HDS3000扫描仪(σs=0.004 m,σθ,α=12″)与NET1200 全站仪(σs=0.001 m,σθ,α=1″)先后观测固定位置的3个平面靶标及5个靶球的几何中心获得,实测数据见表2。

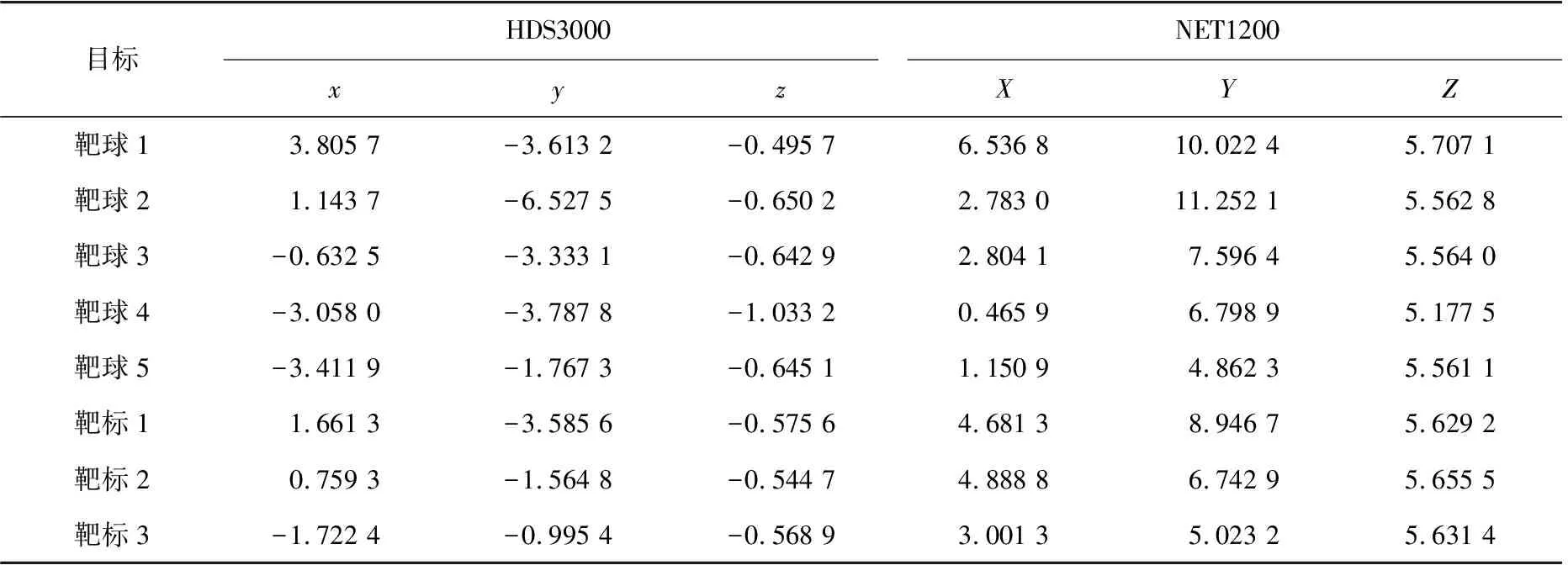
表2 实测坐标数据

以5个靶球作为公共点、3个平面靶标作为检核点。鉴于实测数据没有真值,仅利用仿真实验中的方案1、方案2和方案3对HDS3000扫描仪进行自检校并评定结果。计算过程中认为垂直角与水平角观测精度相同,在获取未知参数估值后,计算公共点与检核点的坐标分量中误差(σx,σy,σz)及点位中误差σp以验证本算法的有效性。

(25)

式中:(xc,yc,zc)为经误差改正后的目标坐标;M表示目标点数量,对于公共点M=5,检核点M=3。计算结果如表3所示。

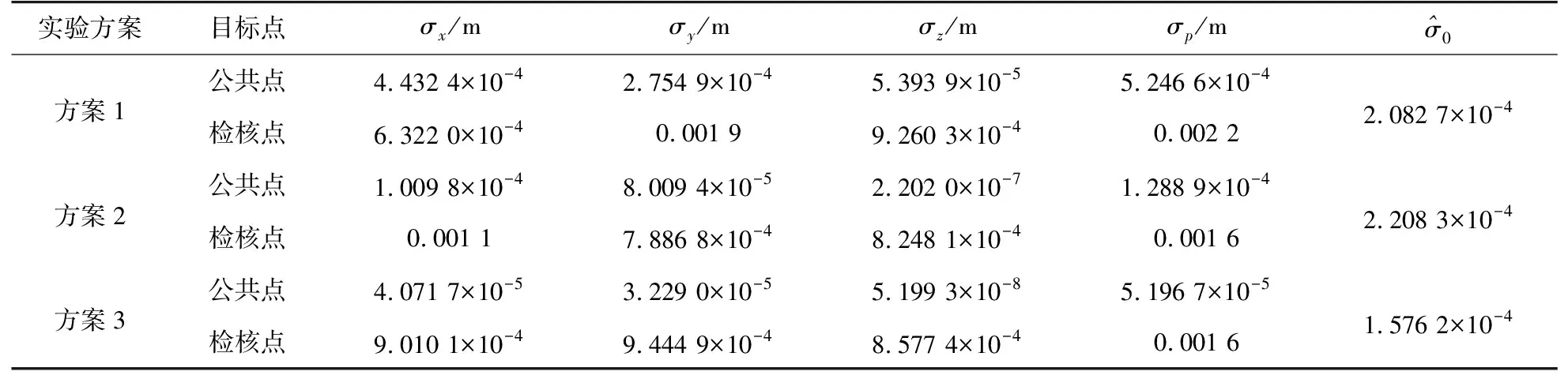
表3 实测数据计算结果

2.3 实验结果分析

由图2～3及表2可知,在仿真实验中不考虑观测值随机误差时,参数估计值与真实值差距最大且变化显著,表明随机误差的存在直接关系到未知参数的解算精度。方案2在函数模型中考虑了扫描仪观测值的随机误差,与方案1相比有一定程度改善,特别是平移参数与垂直角系统误差项。就参数估计精度而言,新算法得到的结果更接近真实值,与方案1和方案2相比具有更优的RMSE且参数估计值更加稳定;根据式(15)中参数的排列顺序,方案3较方案1的参数RMSE分别提高了59%、65%、66%、19%、14%、31%、2%、1%、33%、14%和56%,表明合理剔除观测值中的随机误差可有效提高参数的解算精度。但与距离有关的系统误差改善效果并不明显,可能由于数值相对角度系统误差项较大引起的。

此外,经过系统误差和随机误差改正后,方案2与方案3的公共点的坐标分量误差及点位中误差更小,较方案1与方案4的坐标分量精度提高30%,点位精度提高60%;方案1与方案4的公共点精度具有大致相同的变化趋势,表明了考虑随机误差的必要性。为进一步验证算法的有效性,利用3种方案对没有加入随机误差的检核点进行处理,经误差改正后方案3较方案1与方案2更接近真实全站仪坐标,表明方案3获取的参数估计值更接近于真实值。

实测数据实验中,方案1得到的坐标分量误差及点位中误差均满足仪器的检校需求,原因是在观测过程中仪器与目标的距离较近,观测值中的随机误差可被有效控制,但当仪器精度较低或与目标的距离较远时,上述结果将很难保证。方案3较方案1的点位精度在公共点处提高90%,检核点处提高27%,且验后单位权中误差提高24%;方案3较方案2的公共点点位精度提高60%,检核点精度几乎相同,原因是高精度全站仪观测值的随机误差极小,不足以对结果产生显著影响。方案2的公共点与检核点的精度优于方案1,但验后单位权中误差却有所增加,可能是由标称精度定权导致随机模型不精确引起的。

3 结论

提出一种新的基于Gauss-Helmert模型的TLS自检校方法,与常规方法相比,可同时考虑全站仪和扫描仪观测值的随机误差。仿真数据和实测数据验证表明,该方法可获得更高精度的参数解,且经过系统误差和随机误差修正后的坐标更接近真实值。此外,由于自检校模型是非线性模型,在迭代计算过程中需要不断更新未知参数和随机误差,导致运行时间增加。因此,如何提高计算效率还需要进一步研究。另外,随机模型对于参数估计至关重要,在后续研究中应增加合理的验后估计。