超音速声强近似测量方法

王文璟，张永斌

(1.铜陵职业技术学院，安徽 铜陵 244061；2.合肥工业大学 噪声振动工程研究所，合肥 230009)

结构受到激励产生弯曲波、纵波或横波等弹性波，它们在结构里的传播带动附近的空气形成声波并向外辐射。这就是结构声的产生机理。根据结构波传播速度与声速的相互关系，这些结构波可以分为两类：亚音速波(传播速度小于声速)和超音速波(传播速度大于声速)。其中超音速波引起的噪声能够辐射到远场，是环境噪声污染的主要组成部分；而由于结构表面相邻区域振动的抵消作用，亚音速波无法辐射到远场，只存在于结构的近场区域。因此识别超音速结构波引起的声源振动对于有效控制振动结构的噪声辐射具有重要意义。

声强(通常是有功声强)测量是一种常用的识别声源和评价声源强度的方法，但是由于亚音速结构波的存在，在有些位置处声强的正负值会互相抵消，导致难以识别引起远场声辐射的声源区域。为解决该问题，Williams于1995年首次提出了超音速声强(supersonic acoustic intensity)的概念，并用于水下柱壳的声源识别[1]。特别需要注意，这里的“超音速”与常规含义不同，超音速声强指的是传播速度高于声速的结构波引起的声强分布。这一概念被提出以后，相继被扩展到平面型结构[2-6]和任意形状结构的声源识别[7-10]。在超音速声强的基础上，近年来又延伸出了非负声强(non-negative acoustic intensity)的概念[11-12]。

在测量超音速声强时，既可以先测量声压，也可以先测量质点振速，然后通过近场声全息技术[13-17]计算出声源表面的声压和质点振速，接下来对声压和质点振速进行波数域滤波，去除辐射圆之外的所有倏逝波成分(对应亚音速结构波)，只保留辐射圆之内的传播波成分(对应超音速结构波)。滤波后的声压和质点振速分别被称为超音速声压和超音速质点振速。最后，在超音速声压和质点振速的基础上，采用与有功声强相同的定义方法计算超音速声强。从上述过程可以看到，超音速声强只需近场测量数据，却能表征声源的远场辐射信息，因此可作为噪声控制的一个重要依据。近年来，超音速声强还常被用于分析声学黑洞的作用机理和振动噪声控制效果[18-19]。

在已有的超音速声强测量方法中，需要首先测量声源表面或近场的法向质点振速或声压。目前测试这两个参量的方法有快照法和扫描法两种。其中，快照法使用大通道数测试设备和大型传感器阵列同时测量声场或振动信号。该方法虽然适用于任意声源信号，但是所需测试硬件设备的成本过高，而且不适合在空间较小的环境中使用。扫描法使用小通道数测试设备和小型传感器阵列分步扫描测量声场，所需测试硬件设备的成本低，因此是声阵列测量中的常用方法。但是扫描法需要与声源相关的参考信号而且要求参考信号的数目大于潜在声源的数目，来辅助消除不同次测量之间的相位差[20-21]。但在实际应用中，声源的数目和位置是未知的，因此难以获得满足要求的参考信号。

为解决超音速声强测量受硬件成本和参考信号限制的问题，本文提出一种超音速声强近似测量方法。在该方法中，使用传统的声强探头进行扫描测量。由于复声压和法向质点振速在每一点都是同步测量，初始相位互相抵消，因此传统的有功声强这一参量在不同的测量点不受初始相位的影响，因此也就无需参考信号。然后对有功声强直接进行波数域滤波，得到近似的超音速声强。需要说明的是，通过本文方法测量得到的超音速声强与Williams的定义有所不同，跳过了超音速声压和质点振速的计算，直接从传统声强计算超音速声强，因此是一种近似方法。但是理论推导和数值验证表明本文定义的近似超音速声强具有传统超音速声强的特性，而且可以有效识别引起远场声辐射的声源区域。

1 理 论

1.1 准确超音速声强的定义与计算

假设时间简谐因子为e-iωt,那么在平面z上的波数域声压P(kx,ky,z)和法向质点振速U(kx,ky,z)可以表示为

(1)

(2)

式中，kx和ky分别为x和y方向的波数分量，p(x,y,z)和u(x,y,z)分别表示平面z上的空间域声压和法向质点振速。

对波数域声压和质点振速进行滤波，去除辐射圆(Radiation Circle)之外的倏逝波成分，可以分别得到超音速声压和质点振速为

(3)

(4)

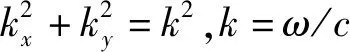
基于式(3)和式(4)以及传统的有功声强的定义，Williams提出的超音速声强的定义为

(5)

式中，上标*表示复数共轭，Re表示取复数的实部。经过数学证明，可以发现通过式(5)定义的超音速声强计算得到的声功率与通过传统的有功声强，即下文式(6)，计算得到的声功率相等。这也是式(5)中的I(s)(x,y,z)之所以被称为声强的根本原因。

在测量超音速声强时，为降低测试成本，通常使用扫描法测量声压(或质点振速)，然后使用近场声全息技术计算对应的质点振速(或声压)，最后将其代入式(1)～(5)计算得到超音速声强I(s)(x,y,z)。但是如引言中所述，使用扫描法测量时，存在参考信号难以获取的限制。

1.2 近似超音速声强的定义与计算

传统的有功声强的定义为

(6)

关于有功声强测量方法的研究是一个经典问题，目前已经研发出了多种声强探头用于有功声强的测量[22-23]。这些探头可以分为两类：一类是使用两个或多个传声器，所需的质点振速通过声压的有限差分获得；一类是同时使用传声器和质点振速传感器(如Microflown)，直接实现有功声强的测量。不管使用哪类声强探头，测试有功声强时，不同的传感器在同一个点都是同时进行测量，因此它们的测量信号具有相同的初始相位。而且由于在式(6)中，质点振速进行了共轭运算，因此最终的声压和质点振速的初始相位被抵消。也就是说使用扫描法测试不同位置的有功声强时不受初始相位变化的影响。虽然有功声强具有这一优点，但是由于亚音速结构波的存在，式(6)定义的有功声强在有些位置处的正负值会互相抵消，导致使用该参量不适合用于识别引起远场声辐射的主要声源区域[1-4]。

基于上述讨论，将有功声强和超音速声强的优点相结合，本文定义一种近似的超音速声强。在声源附近测量得到式(6)定义的有功声强之后，通过二维空间Fourier变换计算其波数谱IK(kx,ky,z)

(7)

然后通过对IK(kx,ky,z)直接进行波数域滤波，去除辐射圆之外的倏逝波成分，只保留辐射圆之内的传播波成分，得到近似的超音速声强为

(8)

式中，Sr与式(3)和式(4)中的含义相同。

检验公式(8)中超音速声强的定义是否合理的关键是由该声强计算得到的声功率是否与由式(6)定义的有功声强计算得到的声功率相同。由式(6)计算得到的声功率为

(9)

对比式(9)与式(7)可以发现kx=ky=0时，两者相等，即Ψ(z)=IK(0,0,z)。

由式(8)计算得到的声功率为

ΨI(s)(z)=

IK(0,0,z)

(10)

因此Ψ(z)=ΨI(s)(z)，也就是说式(8)中定义的参量II(s)(x,y,z)同样具有声强的含义。从定义上来说，式(5)中的准确超音速声强分别对声压和质点振速进行波数域滤波，因此传播波和倏逝波的定义和界限非常明确；但是如式(6)所示，有功声强是由声压和质点振速的共轭相乘得到，因此声压和质点振速分别对应的波数会相互叠加或相减，类似于三角函数的积化和差，导致一些原本不属于辐射圆内的波数通过相互运算后产生位于辐射圆内的波数。因此，式(8)给出的超音速声强定义虽然可以滤除部分倏逝波的影响且能保证声功率不变，从而可以有效识别引起远场声辐射的声源区域，但是不能完全消除倏逝波的影响，因此本文将其称为“近似超音速声强”。

近似超音速声强的测量和计算流程如图1所示。首先使用声强探头在声源的近场逐点扫描测量法向有功声强I(x,y,z)，这里假设法向方向为z向，需要注意扫描时要求x和y方向的测点间隔(即空间采样频率)保持不变，以满足空间Fourier变换的要求。然后对I(x,y,z)进行二维空间Fourier变换，得到法向有功声强的波数域谱IK(kx,ky,z)。由于计算过程使用了二维空间Fourier变换，因此与文献[2]中提出的准确超音速声强类似，这里要求测量面为平面。接下来对波数域谱IK(kx,ky,z)进行低通滤波，将辐射圆之外的波数域谱置零。最后对滤波后的IK(kx,ky,z)进行反空间Fourier变换，得到近似超音速声强II(s)(x,y,z)。

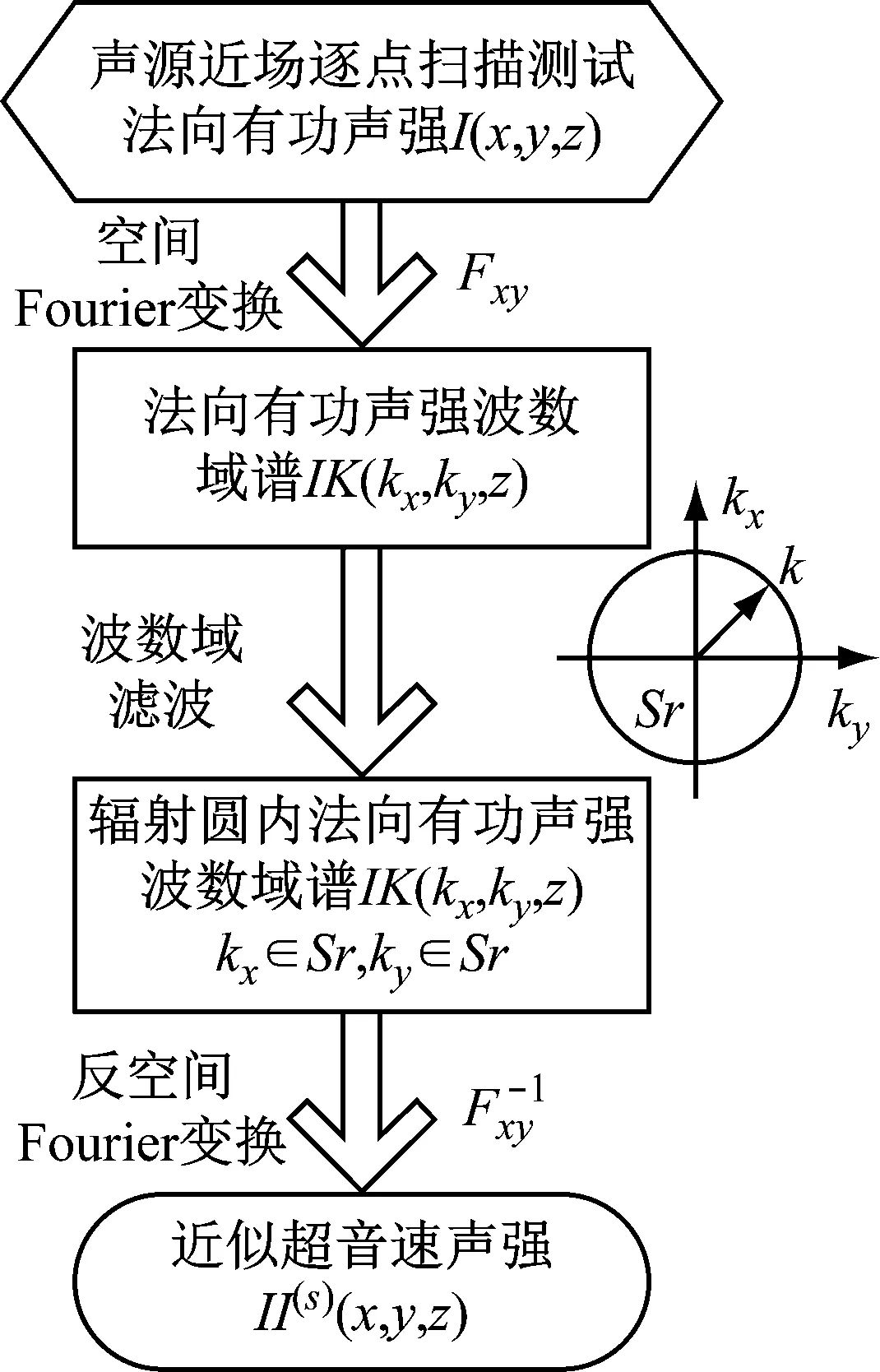
图1 近似超音速声强测量和计算流程Fig.1 Measurement and computational flow of the approximate supersonic acoustic intensity

从计算角度来说，近似超音速声强的误差主要来源于空间Fourier变换。根据上文的变换公式可以看到空间Fourier变换的积分区域是无限大的平面，但实际中只能在有限尺寸的平面上进行扫描测量，也就是说需要对空间进行截断。由于空间截断，空间Fourier变换中会引入卷绕误差。减小卷绕误差的有效方法是对测量数据进行补零。

2 准确和近似超音速声强的对比

2.1 无限大障板上的点源

首先以无限大障板上的点源为例进行对比，选择这个算例的原因是其超音速声强能够推导出解析公式。假设源强为Q的点源位于z=0处的障板上，那么声源表面的法向质点振速u(x,y,0)=Qδ(x)δ(y),声源表面的声压可以通过Rayleigh积分得到：

(11)

则根据式(6)，得到有功声强为

(12)

将式(12)代入式(7)，得到I(x,y,0)的波数谱为

(13)

将式(13)代入式(8)，并引入极坐标变换：kx=kρcosθ,ky=kρsinθ,x=ρcosφ,y=ρsinφ,则可以推导得到近似超音速声强为

II(s)(x,y,0)=

(14)

式中，J0和J1分别为0阶和1阶第一类Bessel函数，上式的推导过程中使用了积分恒等式：

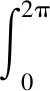
对公式(14)中的II(s)(x,y,0)在整个声源面上进行积分，可得声功率为

(15)

将式(12)代入式(9)可得通过有功声强计算得到的声功率，其结果与式(15)相同。通过这个算例进一步证明了本文定义的近似超音速声强保持了声功率不变，具有声强的特性。

在文献[2]中，针对这个算例，Williams给出了准确超音速声强的表达式为

(16)

对比式(14)和式(16)可以发现，对于无限大障板上的点源而言，本文定义的近似超音速声强与Williams定义的超音速声强仅差sin(kρ)/kρ一项。图2给出了除以ρck2Q2/(8π2)之后的归一化超音速声强的对比，其中图2(a)为线性值，图2(b)为对数值。从图2(a)中可以看到，虽然超音速声强II(s)不如I(s)集中，但是也可以有效地识别出对应远场声辐射的声源区域。上述结论从图2(b)也可得到，虽然II(s)的旁瓣比I(s)的旁瓣峰值更大，但是主瓣的峰值相同，主瓣的中心位置也相同。另外从图2中的I(s)的曲线可以看到，准确超音速声强基本没有负值，因此不存在声源附近的声场正负抵消问题；相比I(s)，本文定义的II(s)的负值数目有所增加，因此II(s)是超音速声强的近似参量，而不是等价参量。

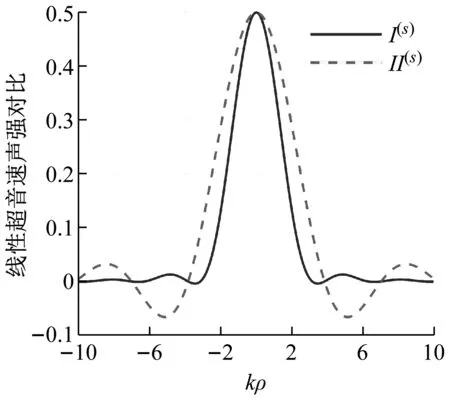
(a) 线性值

(a) 准确超音速声强

2.2 无限大障板中的简支板

该简支板为0.003 m厚的铝板，其长和宽为2 m×2 m。幅值为500 N的简谐力作用在该板的中心对其进行激励。简谐力的频率满足kL=3π，其中L=2 m为简支板的边长。板表面的法向位移由(11,9)阶模态振型产生，距离板表面0.02 m处的声场通过Rayleigh积分数值计算得到。根据文献[2]和文献[24]可知，(11,9)阶模态角模态(Corner modal)，即只有四个角的区域是形成远场声辐射的主要振动区域，而其他区域的振动形成了能量循环，因此并不向远场辐射。

针对该算例，两种超音速声强I(s)和II(s)的计算结果如图3所示。从图中可以看到在I(s)中基本不包含负值，但是在II(s)中仍然存在一些负值，表明在II(s)中仍然残留一些局部能量循环。图4中给出了相同表面上的有功声强计算结果，可以明显看到在简支板中间交叉出现正值和负值，但是这些位置处的能量仅仅形成局部循环，并不对远场声辐射做出贡献。通过图3和图4的对比可以发现，相比有功声强，本文定义的超音速声强II(s)消除了局部能量循环导致的干扰声源，突出了边角模态振型，有效地识别出了引起远场声辐射的声源位置。

图4 无限大障板中的简支板对应的有功声强Fig.4 Active acoustic intensity of a simply supported plate in an infinite baffle

2.3 试 验

实验场景如图5所示，声源为一块铝板，其尺寸为0.44 m×0.44 m×0.003 m，该板做为其中一个面被安装在一个箱体上，箱体的其他几个面为硬质纤维板，并在箱体中安装一个音箱驱动铝板振动。信号采集和发生设备为B&K公司的“PULSE”分析仪(型号3560)。

图5 试验场景Fig.5 Experimental arrangement

为进行对比，以分析仪产生的信号为参考，应用集成了传声器和Microflown质点振速传感器的1/2英寸p-u声强探头，在尺寸为0.425 m×0.45 m的平面上，扫描测量了声压和质点振速，测量点数为18×19点，测量面与板表面之间的距离为0.045 m。将测量得到的声压和质点振速代入式(3)～(5)可以计算得到准确的超音速声强。将测量得到的有功声强代入式(8)可以计算得到近似超音速声强。但是需要注意，为实现扫描测量声压和质点振速，引入了预知的输入信号作为参考信号，但在实际中激励来源和输入信号是难以获取的；相对地，测量有功声强的过程则不需要任何参考信号。这就是本文方法的优势所在。

图6和图7分别给出了在200、800、1 000和2 000 Hz处的准确和近似超音速声强实验测量结果。通过两图的对比可知，除1 000 Hz外，近似超音速声强结果均与准确超音速声强结果比较接近，两者都能定位出主要声源位置，但是相对而言，准确超音速声强结果干扰更少，声源位置更为突出。在1 000 Hz时，如图6所示，准确超音速声强出现了较为明显的负值，也就是说在这个频率处，两种方法的测量结果都存在较大误差。

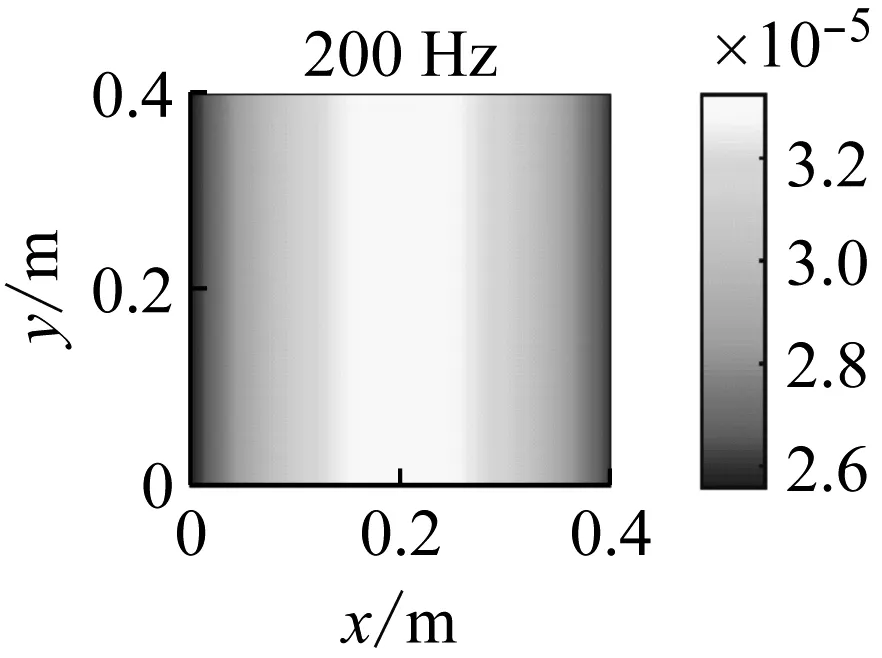
图6 准确超音速声强实验结果Fig.6 Experimental results of the accurate supersonic acoustic intensity

图7 近似超音速声强实验结果Fig.7 Experimental results of the approximate supersonic acoustic intensity

3 结 论

本文提出了一种超音速声强的近似测量方法，在该方法中利用了传统有功声强测量不受初始相位影响的优势，通过在波数域滤除有功声强的倏逝波成分，得到近似的超音速声强。在使用扫描法测量的过程中，不需要任何参考信号是所提出方法的主要优势。之后，从理论上证明了采用本文给出的超音速声强计算得到的声功率与采用有功声强计算得到的声功率的等价性，表明本文定义的超音速声强确实具有声强的含义。开展了以无限大障板上的点源和简支板为声源的数值仿真和以有限尺寸铝板为对象的实验研究，比较了Williams定义的准确超音速声强与本文定义的近似超音速声强，结果表明虽然近似超音速声强的主瓣变宽且旁瓣变大，但是仍可以有效地识别出对应远场声辐射的声源位置。