基于循环生成对抗网络的壁画色彩修复算法

曹建芳,靳梦燕,李朝霞,陈泽宇,马 尚

(1.太原科技大学 计算机科学与技术学院,山西 太原 030024;2.忻州师范学院 计算机系,山西 忻州 034000)

敦煌唐代壁画由于年代久远,出现变色、褪色等问题。传统的人工修复方法依赖于科研工作者对史料的全面了解和丰富的修复经验。随着计算机技术的发展,数字图像处理为壁画修复提供了强大支持,降低了修复难度,减少了对人工修复的依赖。近年来,壁画数字修复技术迅速发展,Pan等[1]提出从壁画高光谱图像捕获从可见光到近红外光光谱范围的图像,有效提取了褪色壁画图案,但当壁画图像不够清晰完整时,该方法的精度较低。Cao等[2]利用高光谱成像技术,提出一种基于暗通道先验和Retinex双边滤波的灰暗壁画修复方法,但对于复杂壁画图像的细节处理仍有待改进。杨筱平等[3]首次采用GrabCut分割算法[4],对壁画图像进行分割和色彩转移自动取样,实现了壁画图像色彩修复。张豪远等[5]在壁画图像中提取局部分割区域的特征,并在多尺度空间中提取纹理特征以确定最佳匹配块,对破损的壁画进行虚拟修复,但无法为大面积破损的壁画图像匹配最合适的特征块,修复效果较差。Liu等[6]使用部分卷积对非规则化破损区域进行修复,但一些结构稀疏的图像会修复失败。焦莉娟等[7]提出一种改进的块匹配修复算法,克服了Criminisi算法[8-9]中的错误填充问题,但只适用于修复跨度较小的破损区域。Li等[10]提出一种基于方向扩散的二阶双曲偏微分方程模型,能有效防止图像阶梯效应的产生,并且保持图像的边缘和细节。

传统修复算法存在语义一致性差、边缘模糊及伪影、难以捕捉高级语义信息等问题,而生成对抗网络(generative adversarial network,GAN)[11]为解决壁画修复问题提供了新的思路。Pathak等[12]首次将神经网络算法引入到无监督的视觉特征学习中,运用卷积神经网络和生成对抗网络,以图像缺失部分的上下文信息作为推理依据,提出一种兼顾整幅图像理解与合理推断的上下文编码器算法,为图像的视觉修复、语义还原提供了全新的解决办法,为后续研究提供了理论借鉴。徐志刚等[13]提出基于双重约束卷积神经网络方法,以解决石窟壁画褪变色问题,但仅适用于结构较为简单的壁画。Song等[14]将壁画图像转换到色彩空间,然后对各分量图像进行高低帽运算,构造多结构形态滤波器平滑图像中的噪声,将融合后的掩膜图像与原始壁画进行融合,提出一种改进的生成式对抗网络结构。朱欣娟等[15]针对文物表面暗旧、图像褪色等问题,提出一种生成式对抗网络的文物图像超分辨率模型,在重建图像纹理时能在一定程度上对褪色图像色彩进行修复,但很难修复表面信息不完整的壁画图像。Cao等[16]提出增强一致性生成对抗网络算法,可对纹理结构强、缺失区域较大的壁画图像缺失部分进行修复,但该算法对数据的质量要求较高。Li等[17]提出一种基于人工智能算法的生成鉴别网络模型,能有效修复具有圆点状损伤和复杂纹理结构的壁画。随着深度学习技术的不断深入,利用神经网络技术实现图像的风格转移,为壁画图像色彩修复提供新途径。Zhu等[18]提出循环生成对抗网络(CycleGAN),首次采用GAN[11]进行图像风格迁移,可以转换无配对图像。Arjovsky等[19]提出WGAN算法,利用Wasserstein距离来代替JS散度和KL散度,从根本上解决了GAN的梯度消失问题。Johnson等[20]提出利用感知损耗函数对前馈网络进行训练,实现了实时风格转换和超分辨率重建。现有的基于深度学习的图像修复方法,对早期训练样本的精度和完整性要求很高,但找到高质量的实际壁画图像需要很高的成本,且很多待修复的壁画图像根本不完整。

现有的壁画修复技术大致可以分为两类:一类为传统的图像修复,另一类为基于深度学习的图像修复。传统修复算法存在语义一致性差、边缘模糊及伪影等问题,而基于深度学习的图像修复方法多需要高精度数据集。本研究以CycleGAN算法[18]为基础,提出一种基于循环生成对抗网络和多尺度融合协调注意力机制的壁画色彩修复算法(multi-scale fusion coordinated attention mechanism CycleGAN,MFCA-CycleGAN),创新之处有:在网络的循环一致性损失中添加同一映射损失改进网络,使生成的壁画图像更加真实可靠;改进协调注意力机制,引入多尺度融合思想,在生成器中加入多尺度融合的协调注意力机制,提高生成壁画图像的协调性和质量。

1 相关技术介绍

1.1 循环生成对抗网络

CycleGAN包含两个判别器和两个生成器,无需预先匹配,就可以进行数据之间的转换。在此基础上,内容图像通过生成网络和判别网络,生成风格化图像。CycleGAN主要包含两部分损失,分别为对抗损失和循环一致损失。

1) 对抗损失

GAN是CycleGAN的基础,利用对抗损失不断优化生成器和判别器。CycleGAN也利用此对抗损失优化网络,通过判别器对生成样本和真实数据进行鉴别,生成器希望生成样本被判定为真,而判别器要识别出图像是真实的还是生成的。对于生成器G:X→Y,其判别器DY的损失函数为:

LGAN(G,DY,X,Y)=Ey～Pdata(y)[lnDY(y)]+Ex～Pdata(x)[ln(1-DY(G(x)))]。

(1)

式中:X、Y为两个图像域;x、y为两个域中的图像;DY(y)为图像y属于域Y的概率;Ey～Pdata(y)为y取自Y的期望;Ex～Pdata(x)为x取自X的期望。

对于生成器F:Y→X,其判别器DX的损失函数为:

LGAN(F,DX,Y,X)=Ex～Pdata(x)[lnDX(x)]+Ey～Pdata(y)[ln(1-DX(F(y)))]。

(2)

式中:F为域Y向域X的映射函数;DX(x)为图像x属于域X的概率。

2) 循环一致性损失

CycleGAN同时进行G、F映射,将图片转换后还可以进行还原,有效避免了所有X图像转换为Y图像域中的同一图像的情况。循环一致性损失为:

(3)

式中:Ex～Pdata(x)[]为域X中图像x经生成器G作用后生成G(x),G(x)再由生成器F作用变为F(G(x)),F(G(x))应与图像x近似。Ey～Pdata(y)同理。

CycleGAN的基本原理如图1所示。网络的所有损失相加即为CycleGAN的目标损失

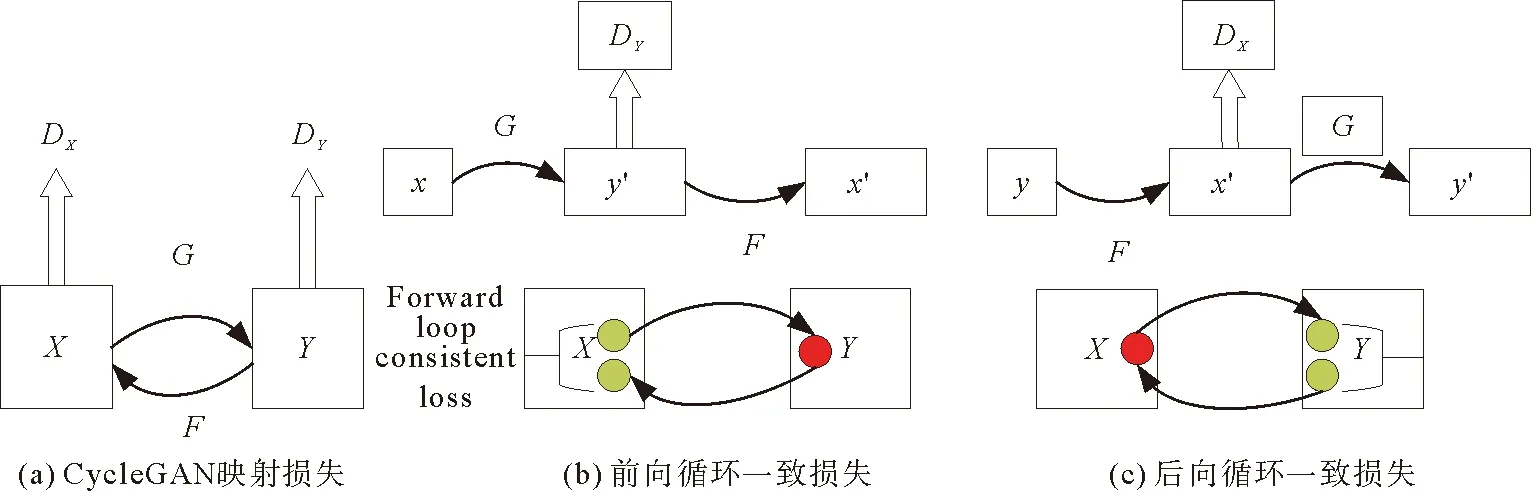
图1 CycleGAN原理图

L(G,F,DX,DY)=LGAN(G,DY,X,Y)+LGAN(F,DX,Y,X)+λLcyc(G,F)。

(4)

式中,λ为控制各损失间相对重要程度的加权因子。

1.2 协调注意力机制

注意力机制被广泛用于提高现代深层神经网络的性能。Hou等[23]基于挤压和激励网络(squeeze-and-excitation networks,SENet)[21]和卷积块注意力模块(convolutional block attention module,CBAM)[22],将位置信息嵌入通道中,使移动网络能够在大范围内关注,同时避免了巨大的计算量。位置信息嵌入通道注意,将一个二维的池化操作转换为两个一维的池化操作,沿着两个方向聚合特征,生成的特征映射被分别编码成方向感知和位置敏感的注意映射,用于提高感兴趣对象的输入特征的表示。具体地,为了激励注意力模块以精确的位置信息在空间上捕获远程交互,给定输入x,分别从水平与垂直方向进行重要特征提取,高度h上的第c个信道的输出[23]

(5)

式中:x来自具有固定内核大小的卷积层,W为图像的宽度。类似地,宽度w处第c个信道的输出可写为:

(6)

式中,H为图像的高度。

给定式(5)、式(6)生成的聚合特征图,首先进行拼接,然后利用一个共享的1×1卷积变换函数F1,得到

f=δ(F1([Zh,Zw]))。

(7)

式中:δ为非线性激活函数;f∈RC/r×(H+W)为水平、垂直方向编码空间信息的中间特征图;r为缩减比,用来控制块大小,然后将f分为两个独立张量fh∈RC/r×H和fw∈RC/r×W。利用另外两个1×1卷积变换Fh和Fw将fh和fw变换为与输入X具有相同信道数的张量,得到:

gh=σ(Fh(fh)),

(8)

gw=σ(Fw(fw))。

(9)

式中,σ为sigmoid函数。使用适当的缩减率r以减少f的信道数,然后将输出gh和gw分别展开用作注意力权重,则坐标注意力块Y的输出为:

Y=X×gh×gw。

(10)

2 基于循环生成对抗网络的壁画色彩修复

循环一致性损失将还原图像F(G(x))与真实图像x、还原图像G(F(y))与真实图像y的损失考虑在内,然而这种端到端的损失未能详尽考虑其转化过程中的风格损失,因此本研究在CycleGAN循环一致性损失函数中添加同一映射损失。而协调注意力机制从横向和纵向两个角度对输入图像进行注意力筛选,缺少综合周围语义信息的有效手段,因此为协调注意力机制添加多尺度融合策略,使得网络模型能够从多方面的特征信息中筛选最为有效的特征信息。从逻辑层面来说,本研究方法使用多尺度融合的协调注意力机制对CycleGAN生成模块中的上采样区域进行特征筛选,在训练过程中利用同一映射损失降低图像转化过程中的风格损失,经过多次循环训练使得CycleGAN最终实现良好的风格迁移。

2.1 同一映射损失

CycleGAN算法的循环一致性损失函数将图像还原之后计算与原始输入图像的差值并求和,在一定程度上可以计算出原始图像与还原图像的差异,但是未考虑生成图像G(x)与真实图像y的损失和生成图像F(y)与真实图像x的损失。以原始图像x到生成图像G(x)再到还原图像F(G(x))为例(其中,真实图像x与真实图像y为不成对图像),由原始图像x到生成图像G(x)的生成损失较生成图像G(x)到还原图像F(G(x))的损失更为重要,如果生成图像与真实图像y的风格损失很大,后续的生成图像G(x)到还原图像F(G(x))的变换也不会成功。本研究基于此改进了循环一致性损失函数,在原始循环一致性损失的基础上加入同一映射损失,即

Lcyc(G,F)=Ex～Pdata(x)[(1-λ1)‖F(G(x))-x‖1+λ1‖G(x)-y‖1]+

Ey～Pdata(y)[(1-λ2)‖G(F(y))-y‖1+λ2‖F(y)-x‖1]。

(11)

式中:λ1为x→G(x)≈y过程中的损失权重,(1-λ1)为F(G(x))≈x过程的损失权重,整个过程中损失之和为1。同理,λ2为y→F(y)≈x过程损失权重,(1-λ2)为G(F(y))≈y过程损失权重。

图2为算法模型的训练流程框架。以正向循环为例,具体训练过程为:首先将真实未修复唐代壁画图像x输入,由生成器G生成修复的唐代壁画图像G(x);然后利用判别器DX判断生成图像是否为真,并将输出反馈到生成器G进行对抗博弈;最后通过生成器F还原为验证的未修复唐代壁画图像F(G(x)),利用循环一致性损失和同一映射损失,确保最终验证壁画图像与真实壁画图像尽可能相似。

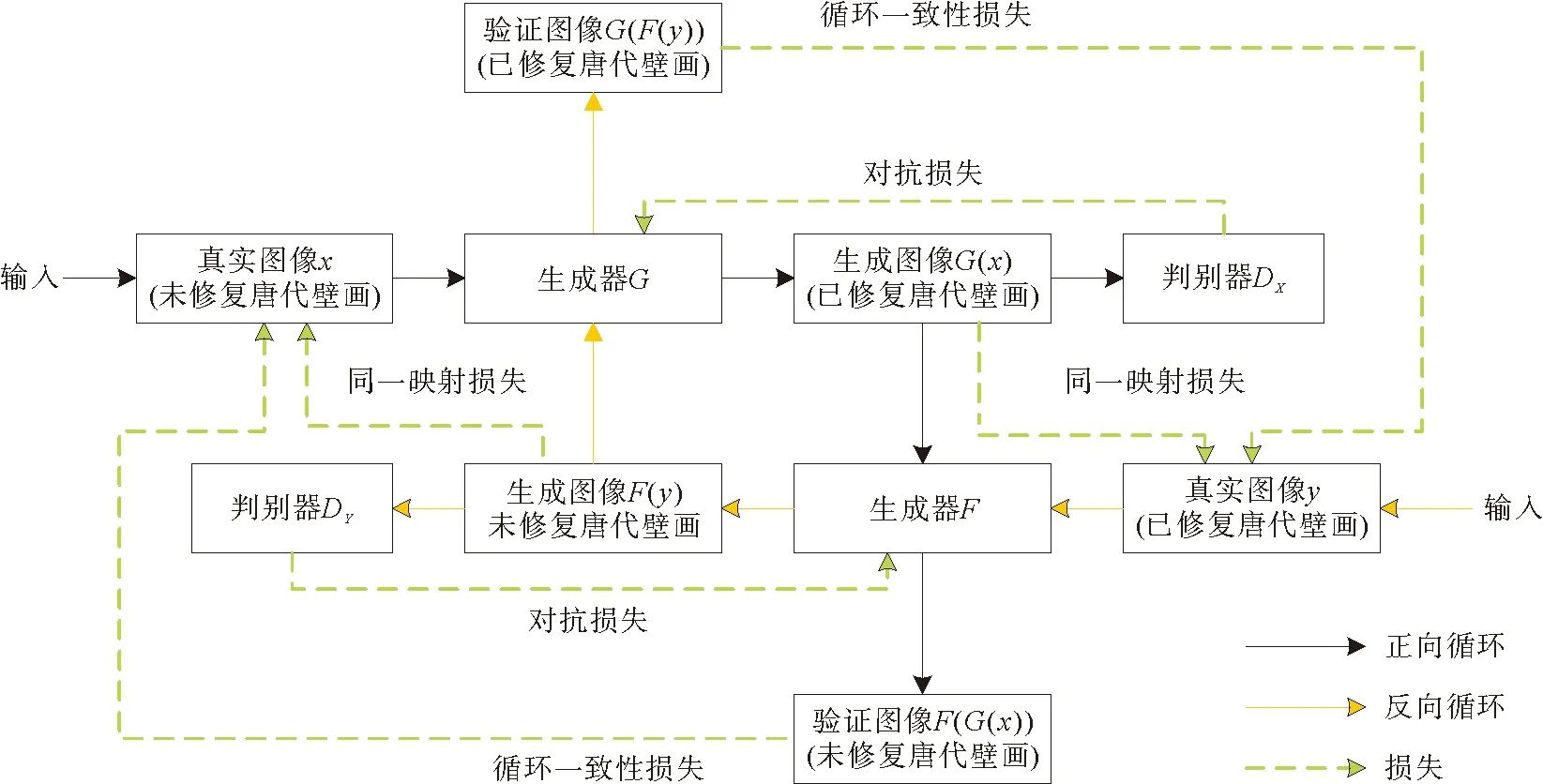
图2 模型训练框架图

2.2 多尺度融合协调注意力机制

协调注意力机制只考虑横纵两个方向的重要性,未从整体上考虑周围语义信息的重要性程度,本研究对协调注意力机制网络结构进行改进,加入多尺度特征融合思想,构成多尺度融合的协调注意力机制。首先对输入图像分别进行卷积核大小为1×1、3×3、5×5、7×7的多尺度卷积运算,得到不同感受野大小的特征信息;然后对四个通道进行特征融合,从横纵两个方向进行适应性平均池化、维度拼接与卷积操作,以及批量归一化与非线性激活;随后分别在横纵两个方向使用Sigmoid函数进行重要性程度判别,对特征图进行权重赋值;最后通过在生成器G的上采样区第2层引入多尺度融合的协调注意力机制,建立图像各个位置像素间关联关系,提高生成图像的协调性和质量。

改进后的生成器G由三部分组成,分别为:由卷积神经网络组成的下采样区域,从输入图像和风格图像提取特征表达;由残差网络组成的中间区域进行图像转换;由反卷积神经网络与多尺度融合的协调注意力机制组成的上采样区域。具体生成模块结构见图3。

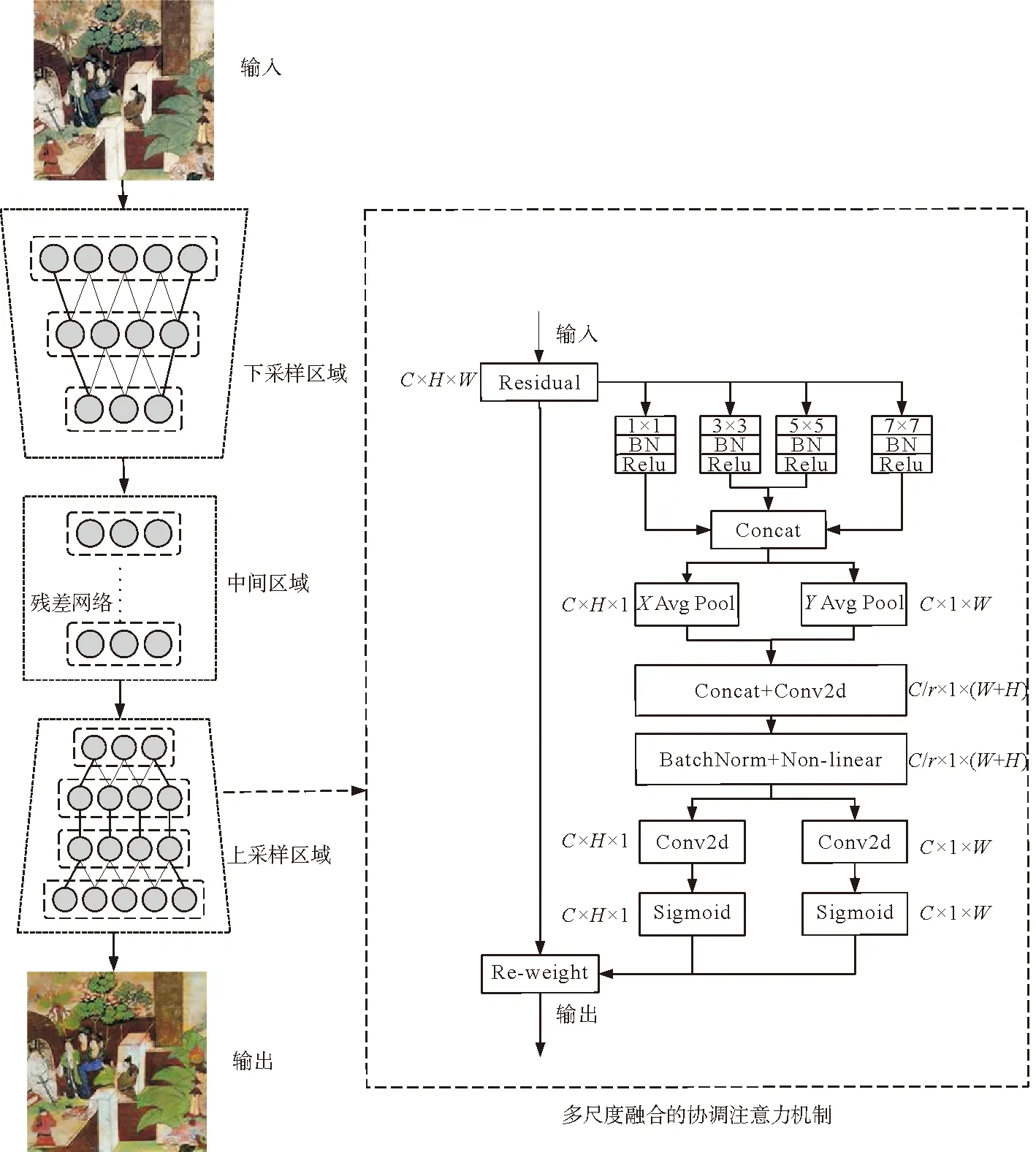
图3 生成模块结构图

2.3 算法步骤

常见的算法描述方法有自然语言、结构化流程图、伪代码等,本研究参考文献[7]采用自然语言方法对算法进行形式化定义。

MFCA-CycleGAN算法的输入包括未修复壁画图像x与已修复壁画图像y,输出为利用风格迁移方法色彩修复后的壁画图像G(x)。具体步骤为:首先,对于输入的未修复壁画图像x与已修复壁画图像y,经过生成网络G生成已修复壁画图像G(x)与还原的已修复壁画图像G(F(y)),再经过生成网络F生成未修复壁画图像F(y)与还原的未修复壁画图像F(G(x));然后,将生成网络梯度设置为0,利用式(11)计算同一映射损失Lcyc(G,F)对生成网络进行反向传播,计算生成网络G、F的梯度并更新权重参数,再使用均方根误差计算判别器DX、DY的梯度并更新权重参数;最后,重复上述步骤,迭代n次得到最优模型,输出本研究算法(以下简称本算法)色彩修复后的壁画图像。

本算法模型需要迭代n次,数据集包含m条数据。m条数据经过前向传播生成对应的风格图像、梯度函数计算等均需要经过n×m次循环迭代来更新网络模型参数,因此本算法时间复杂度为O(nm)。

3 实验结果及分析

3.1 实验环境

使用Python 3.8和Pytorch 1.8.1搭建实验网络验证本算法对壁画图像色彩修复的有效性。其中,硬件环境为Intel i5-9400F处理器、NVIDIA GeForce RTX 2060 SUPER显卡、16 GB内存,软件环境为Windows 10操作系统、Pycharm集成开发环境。

3.2 数据来源

实验使用图像数据集为《中国敦煌壁画全集》电子资源画册的唐代未修复壁画图像和人工修复的唐代壁画图像的截图。其中,未修复壁画图像692张、人工修复壁画图像572张。

3.3 实验结果与分析

3.3.1 模型训练

将未修复壁画图像和人工修复壁画图像按照8∶2的比例进行划分。其中,训练集包括已修复壁画图像458张和未修复壁画图像554张,测试集包括已修复壁画图像114张和未修复壁画图像138张。初始学习率设置为0.000 2,Epoch设置为100,网络中的超参数设置为10,Batchsize设置为8。λ1与λ2为自优化超参数,初始设置均为0.2。图4为原始壁画图像,图5为100次迭代训练之后的壁画修复效果。

图4 原始壁画

图5 修复壁画

从图5可以明显看出,修复后的壁画色彩更加鲜艳,色彩饱和度更高,基本延续了原始壁画的色彩,并对原始壁画的色彩进行了很好的视觉效果增强,具有较高的可信度。

3.3.2 局部褪色壁画图像修复对比实验

将人工修复的壁画图像裁剪为224×224像素大小的壁画图像,并对裁剪后的壁画图像进行矩形区域随机去色处理,获得局部褪色的壁画图像数据集。分别应用文献[18-20]算法和本算法进行壁画局部色彩修复实验,结果如图6所示。

图6 局部褪色壁画图像的不同算法实验结果

文献[18]算法修复后的壁画图像整体模糊,如图6(c)第2张,虽将壁画图像褪色部分进行了修复,但修复效果不佳。文献[19]算法修复后的壁画图像在色彩细节上与原始壁画图像差异较大,如图6(d)第4张。文献[20]算法修复后的壁画图像效果均不理想。

本算法整体效果较好,但在局部壁画色彩修复方面存在不理想的情况。经分析,出现这种情况是由于在同一映射损失函数计算过程中,x→G(x)≈y和y→F(y)≈x损失的存在,弱化了原始CycleGAN中的循环损失函数,图像生成时更加关注整体图像风格的迁移,使部分区域未能得到有效修复,但从实验效果可以看出,相较其他算法,采用本算法修复的局部褪色壁画图像效果最好。

3.3.3 壁画图像整体色彩修复对比实验

分别应用文献[18-20]算法以及本算法进行壁画图像色彩修复对比实验,实验结果如图7所示。本研究利用结构相似性(structural similarity,SSIM)、图像峰值信噪比(peak signal to noiseratio,PSNR)、学习感知图像块相似度(learned perceptual image patch similarity,LPIPS)、Frechet Inception距离得分(Frechet Inception distance score,FID)以及用户调研评价(user study,US)对色彩修复后的壁画图像进行评价。一般情况下,PSNR越高,对应的图像修复效果越好;SSIM取值为[0,1],其值越高图像相似度越高;LPIPS与人类感知情况更为相似,当数值较低时,两幅图片的相似性会更大;FID是一种专门用来评估生成对抗网络性能的方法,将生成的壁画图像与真实的壁画图像进行对比计算“距离值”,该值越小,图像质量越好。不同算法的定量指标对比如表1所示。

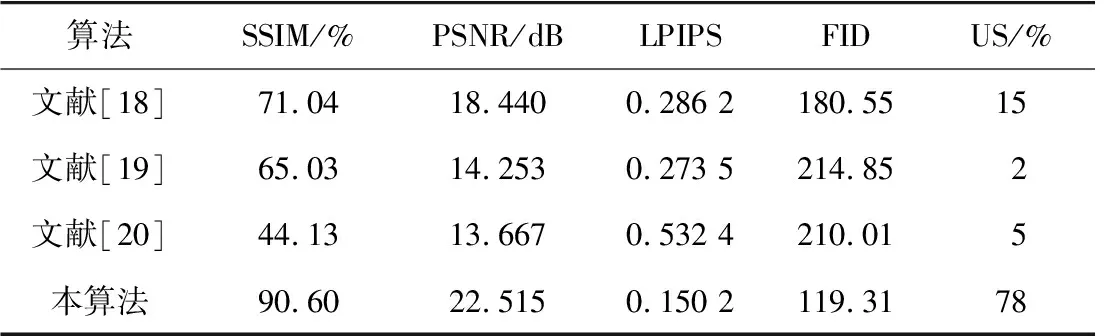
表1 不同网络的定量指标对比

图7 整体壁画图像色彩修复不同算法实验结果

从SSIM和PSNR看,本算法在4组图像中最高,分别达到90.60%和22.515 dB;从LPIPS和FID看,本算法4组图像中最低,分别为0.150 2和119.31。对比实验结果可以看出,本算法可以获得更加清晰可靠的色彩修复图像,节省了修复时间,提高了修复质量,达到更真实的视觉效果。与其他方法相比,本算法的修复效果更合理、主观视觉更顺畅,在整体颜色重建上有很好的效果。

通过调研100名视力正常的用户,78%的用户认为本算法修复的壁画图像是最佳图像。为了证明本算法修复的壁画图像在主观评价上更具有普遍性,采用评分法对该100名用户进行以人眼主观感知为评价标准的主观评价,得到对4种算法修复的壁画图像清晰度及色彩饱和度的打分结果(评分为5分制:优,5分;良,4分;中,3分;差,2分;劣,1分),并对打分结果分别求平均值,得到的评分结果如图8所示。评分结果显示,本算法修复的壁画图像评分均较高,与其他算法相比,在主观评价上效果更好。

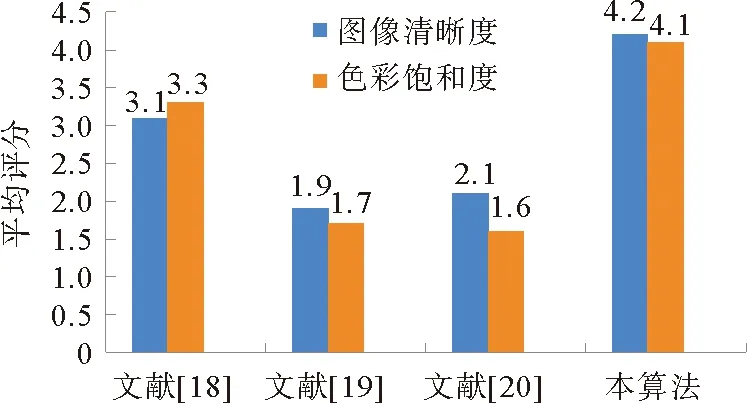
图8 不同算法无参照主观评分对比图

3.4 消融实验

3.4.1 权重系数实验分析

以文献[18]中原始代码为基础进行消融实验,测试原始CycleGAN与本算法所设置参数壁画色彩修复效果,实验结果如图9所示。表2为采用经典PSNR和SSIM定量评价指标,对色彩修复后的壁画图像进行评价。

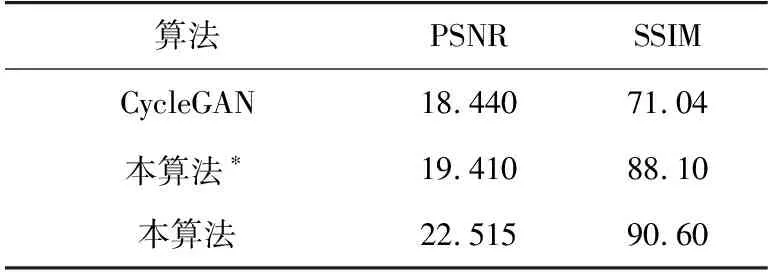
表2 消融实验定量指标对比

图9 消融实验结果图

从图9可以明显看出,原始CycleGAN修复后的壁画图像色彩效果较差,在部分壁画图像中出现了明显的棋盘效应。而当λ1=λ2=0.2时,壁画的色彩修复效果最好,色彩过渡更加自然,且无明显棋盘效应。此外,从PSNR和SSIM看,使用参数λ1=λ2=0.2修复的壁画图像较原始CycleGAN分别提高0.97%和17.06%。

3.4.2 多尺度融合协调注意力机制实验分析

在3.4.1节权重系数实验的基础上,对多尺度融合的协调注意力机制进行消融实验,实验结果如图10所示。

实验表明,使用多尺度融合的协调注意力机制善于捕获全局细节,对于图像修复效果起到至关重要的作用。如图10(c)中壁画图像较原壁画图像色彩更加鲜艳,引入多尺度融合的协调注意力机制有明显的效果提升,对壁画图像颜色的还原起到良好作用。从评价指标看,添加多尺度融合协调注意力机制修复的壁画图像与仅添加权重系数修复的壁画图像相比,PSNR和SSIM分别提高3.105%和2.50%。

3.5 模型复杂性分析

为了分析本算法与其他方法的复杂性,参考文献[24],选用参数量、运算量与单次训练耗时作为算法模型复杂度评价指标。其中,参数量指网络的总参量,与空间复杂度相对应;运算量指网络中浮点运算总量,与时间复杂度相对应;单次训练耗时为对应网络模型迭代一次所需平均时间。实验结果见表3。

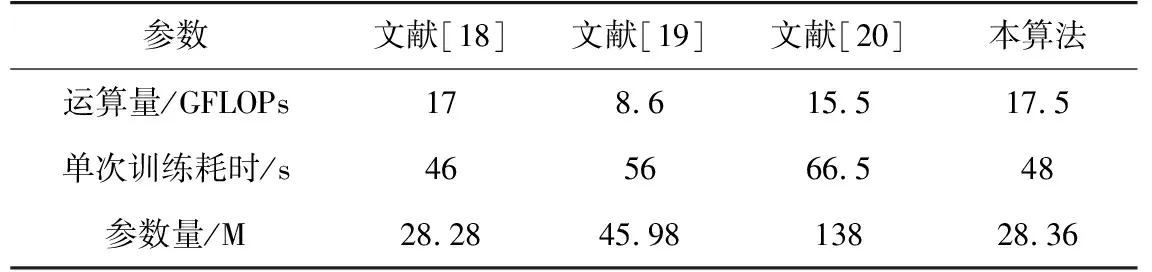
表3 模型复杂度分析

与文献[18]相比,本算法模型复杂度仅与同一映射损失函数以及多尺度融合的协调注意力机制有关。而在同一映射损失函数的计算过程中,相关变量无需重复计算,故对模型复杂度的影响微乎其微。因此,多尺度融合的协调注意力机制对本算法复杂度的影响最大。参照表3可知,在与文献[18]参数量、运算量和单次训练耗时大致相当的条件下,本算法模型在实际壁画色彩修复中取得最佳效果。从单次训练耗时来看,本算法的速度明显快于文献[19]和文献[20],满足速度要求。

此外,本算法虽然在运算量上与文献[19]存在较大差距,但是从实际修复效果来看,本算法色彩修复后的壁画图像色彩更加鲜明且真实细腻。相比于其他3种算法,本算法从主、客观层面都取得了较为理想的效果,性能有较好提升。

4 结论

针对敦煌唐代壁画色彩难以较好修复的问题,提出基于循环生成对抗网络和多尺度融合协调注意力机制的壁画色彩修复算法。首先将同一映射损失加入到循环一致性对抗损失函数中,然后在生成器中引入多尺度融合的协调注意力机制,得到最优的壁画色彩修复网络模型。对比文献[18-20]的3种算法,SSIM分别提高16.59%、25.57%、46.47%,达到90.60%;PSNR分别提高4.075、7.992、8.848 dB,达到22.515 dB;LPIPS分别降低0.136 0、0.123 3、0.382 2,为0.150 2;FID分别降低61.24、95.54、90.7,为191.31。采用无参照主观评价验证表明,改进后的算法在壁画图像色彩的修复上具有有效性和卓越性。最后,通过对权重系数及多尺度融合的协调注意力机制进行消融实验,验证本算法可以在不依赖专家知识的情况下恢复褪色壁画图像的颜色,节省了壁画修复时间。