损伤效应下天然气水合物产气规律模拟研究

王祥阜,邱 月,梁 伟,赵同彬

(1.山东科技大学 能源与矿业工程学院,山东 青岛 266590;2.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;3.中国矿业大学 深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116 )

天然气水合物赋存条件复杂且赋存状态不稳定,压力或温度变化极易诱导其分解[1]。降压法是目前应用最广泛的天然气水合物开采方法,开采过程是一个涉及温度-渗流-应力-化学(thermo-hydraulic-mechanical-chemical,THMC)的多相态多组分多场耦合的复杂过程。水合物降压分解将导致含水合物的沉积物固体结构损伤,应力场及相关耦合物理场将会随之变化。忽略水合物的分解损伤效应将导致天然气水合物分解过程的表征和产气量的预测产生偏差。

国内外学者针对天然气水合物沉积物的损伤效应开展了一系列研究。朱万成等[2]认为损伤会对渗流场、温度场及应力场产生不可忽视的影响,并提出针对岩石类多孔介质的损伤演化方程,但未对天然气水合物沉积物的损伤效应进行系统研究;李彦龙等[3]基于Drucker-Prager准则和Weibull分布的基本假设,建立了同时描述含水合物沉积物应变软化规律和应变硬化规律的损伤统计本构模型;颜荣涛等[4]建立了考虑水合物赋存模式的含水合物沉积物损伤本构模型,并研究了模型参数与水合物饱和度和试验围压之间的关系;祝效华等[5]基于复合材料细观力学混合率理论和岩石孔隙损伤理论,建立了含水合物沉积物等效变弹性模量损伤本构模型,考虑了水合物含量、围压和沉积物内部孔隙变化对含水合物沉积物弹性模量及损伤的影响,但模型参数较多,物理意义不明确;张小玲等[6]提出了考虑损伤阈值和残余强度影响的含水合物沉积物损伤本构模型,将该损伤本构关系代入天然气水合物THMC多场耦合模型,并讨论了结构损伤对沉积物参数的影响规律,但该模型将沉积物屈服应力点作为损伤阈值点的合理性有待评估。以上有关天然气水合物损伤效应的研究,主要是结合Weibull分布建立统计损伤关系,进而建立起沉积物的损伤本构关系,对水合物的分解损伤考虑较少,无法体现水合物本身的强度衰减,同时对水合物分解过程中的损伤效应及其对产气的影响规律有待进一步探究。

本研究考虑天然气水合物分解过程中的损伤效应,建立了耦合温度-渗流-应力-化学(THMC)的多物理场数值模型,研究不同降压幅度、初始绝对渗透率、初始孔隙度对沉积物损伤及产气规律的影响。

1 天然气水合物THMC全耦合数学模型

1.1 天然气水合物全耦合关系分析

天然气水合物的分解吸收热量并产生甲烷气体和水,影响气体和水的渗流过程,同时改变了多孔介质的温度和承载结构,对温度场和应力场产生影响;气体和水的渗流会改变介质内的孔隙压力和有效应力,使得天然气水合物处于相平衡曲线的下方,促进水合物的进一步分解,同时渗流过程伴随着能量转移过程,气体和水的渗流携带了热量,改变多孔介质的温度;多孔介质的温度影响水合物的相平衡状态及分解速率,同时改变了渗流气体的密度并产生热应变;多孔介质应力状态变化导致渗透率、孔隙度和孔隙压力的改变,改变了水合物分解的相平衡条件,影响渗流过程并造成热传导系数、比热容等热力学参数的变化。

为建立天然气水合物THMC全耦合模型,在文献[7]模型基本假设基础上,认为水合物及沉积物遵循各向同性,且始终为弹性,同时以沉积物作为骨架,水合物、水及气占据沉积物全部孔隙体积,即三相的饱和度之和为1。

1.2 分解动力学方程

天然气水合物分解采用Kim-Bishoni分解动力学方程来描述[8-10],分解速率为:

(1)

式中:φ为水合物分解过程中任意时刻孔隙度;ρh为水合物密度,917 kg/m3;Sh为水合物的饱和度;kd为动力学反应速率,Pa·s;Mh为水合物摩尔质量,0.124 kg/mol;As为水合物反应比表面积,与渗透率相关,m-1;Pe为相平衡压力,MPa;Pg为气体动态压力,MPa。

1.3 气水两相渗流方程

天然气水合物岩芯气-水两相渗流质量守恒方程为[11]:

(2)

(3)

式中:ρg、ρw分别为甲烷和水的密度,kg/m3;Sg、Sw分别为甲烷和水的饱和度;k为水合物沉积物绝对渗透率,mD;krg、krw分别为甲烷和水的相对渗透率;μg、μw分别为甲烷和水的动力黏度,分别为1.84×10-5Pa·s和1.01×10-3Pa·s;Pw为岩芯内水的压力,MPa;mg、mw分别为天然气水合物的产气速率和产水速率,kg/(m3·s)。

1.4 传热方程

天然气水合物分解过程中热量变化可表示为[12]:

(4)

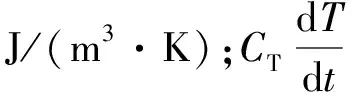
CT=(φ(ρwSwCw+ρgSgCg+ρhShCh)+(1-φ)ρsCs),

(5)

QT=-▽((φ(Swλw+Sgλg+Shλh)+(1-φ)λs)▽T),

(6)

QA=▽(φSwCwρwμwT+φSgCgρgμgT),

(7)

(8)

q=h(Tc-T)。

(9)

式中:Cw、Cg、Ch、Cs分别为水、甲烷、水合物固体和沉积物的比热容,J/(kg·K);ρs为沉积物的密度,取值2 150 kg/m3;λw、λg、λh、λs分别为水、甲烷、水合物固体和沉积物的热传导系数,W/(m·K);μw、μg分别为水和甲烷的达西流速(m/s);mh为水合物分解速率,kg/(m3·s);C1、C2分别为方程回归系数;h为边界热传导系数,W/(m3·K);Tc为岩芯水浴温度,275.45 K。热传导方程的初始条件为:

T=T0。

(10)

式中,T0为岩芯初始温度,取275.45 K。

1.5 力学损伤方程

以位移形式表示的平衡微分方程中考虑了孔隙压力及温度变化的影响,其张量形式表示为[2,13]:

(11)

式中:G为剪切模量;ν为泊松比,取值为0.2;Fi和ui分别为体力和位移在i方向上的分量;α为Biot系数,取值为0.4;αT为介质整体的热膨胀系数,取值为8×10-6K-1;K′为排水体积模量;p为等效孔隙压力。

将孔隙度视为变量,并耦合所有物理场控制方程,孔隙度与体应变的关系可表示为[14]:

(12)

式中:ε、ε0分别为任意时刻和初始时刻的体积应变;φ0为岩芯水合物饱和度为0时的孔隙度,即初始孔隙度。

根据Hyodo等[15]的水合物实验数据可以获得弹性模量与水合物饱和度的关系:

Eh=E0·exp(aE·Sh)。

(13)

式中:Eh为水合物任意时刻的弹性模量,GPa;E0为水合物饱和度为0时沉积物的弹性模量,取值为4.6 GPa;aE为损伤折减系数,取值为1.7。

根据弹性损伤理论,单元的弹性模量和损伤变量之间的关系式为[2]:

Eh=(1-D)Et0。

(14)

式中:Et0为水合物沉积物初始状态(未分解)的弹性模量,GPa;D为损伤变量。这里假定损伤及其演化均为各向同性的,故Eh、Et0和D均为标量。

天然气水合物沉积物初始状态弹性模量为:

Et0=E0·exp(aE·Sh0)。

(15)

式中,Sh0为水合物的初始饱和度。

联立式(13)和(15),得到天然气水合物沉积物损伤的演化表达式:

(16)

2 含损伤天然气水合物全耦合数值模型验证

为进一步验证构建的天然气水合物THMC全耦合数学模型,对比分析了Masuda试验[16]和THMC模型的产气量与温度变化。模型尺寸、初始条件及边界条件如图1所示。Berea岩芯模型长度300 mm,直径51 mm,置于温度为2.3 ℃的恒温水浴中。试验以左端为出口,出口端保持2.84 MPa的恒定压力,其他边界为无流动边界,并对岩芯施加4 MPa的恒定围压。在模型中布置3个监测点A、B、C,分别位于中轴线距降压端的35、150和225 mm处,记录测点温度和累积产气量。除模型基础参数外[7],其他相关参数见表1所列。

表1 模型参数

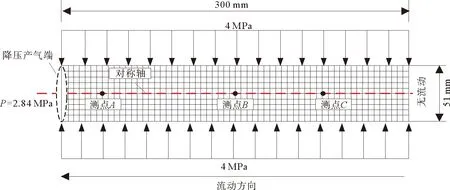
图1 模型的初始条件与边界条件

图2(a)为THMC模型降压分解后0～300 min的累积产气量与Masuda试验结果对比图。水合物初期产气较快而后逐渐放缓,进入稳定产气阶段,数值模拟的累积产气量结果相较于试验结果减小了228.4 cm3,整体相差较小。图2(b)为模型降压分解后0～300 min的温度试验结果对比图,水合物快速分解吸收热量,温度下降较快,稳定产气后温度逐渐回升至水浴温度,分解过程最低温度相差约1.6 K,模拟结果整体趋势与试验数据的吻合较好。

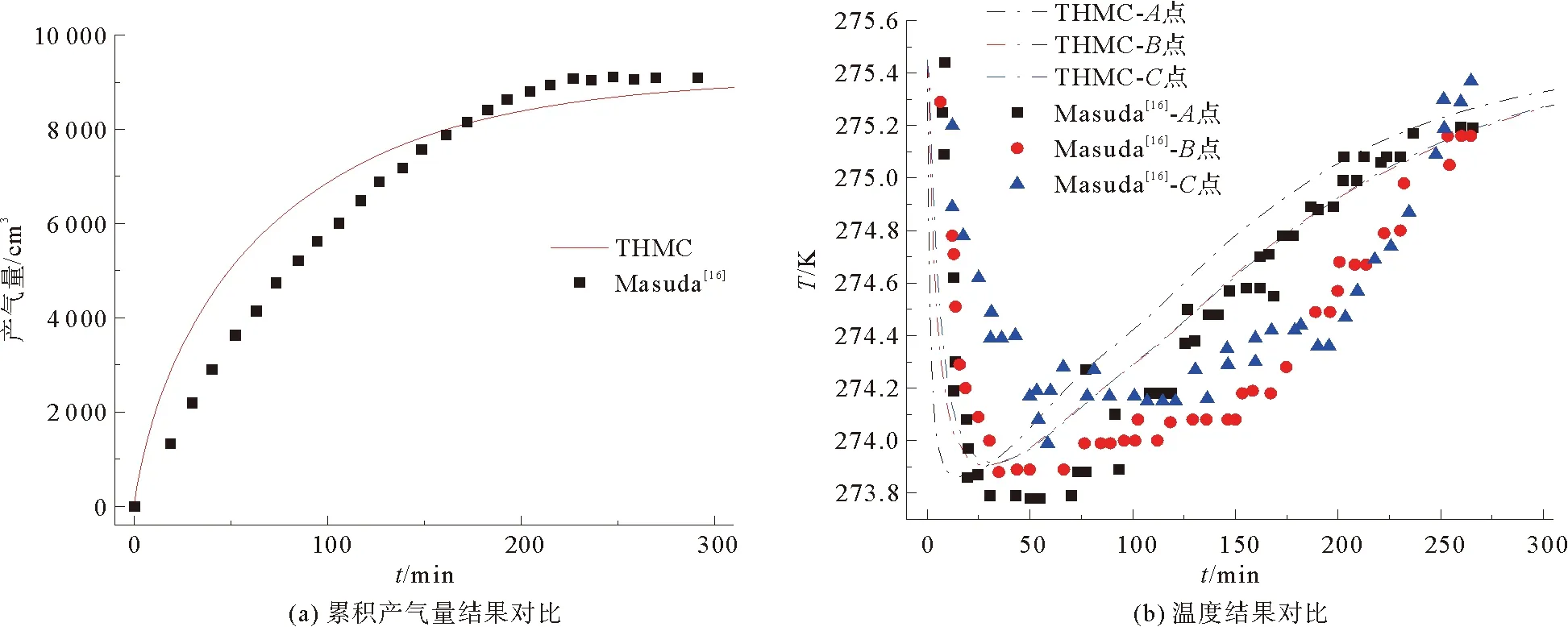
图2 THMC数值模拟结果验证

3 损伤效应下天然气水合物产气影响因素及规律分析

为探究天然气水合物的分解损伤效应及其对产气规律的影响,以Masuda试验模型为基础,选取A点为监测点,讨论损伤效应下降压幅度、沉积物初始绝对渗透率和沉积物初始孔隙度对天然气水合物产气速率的影响。

3.1 不同降压幅度影响分析

天然气水合物分解过程中损伤变量的变化不仅体现了沉积物弹性模量的下降,也表征了水合物饱和度的变化,当水合物饱和度为0时,损伤变量达到最大值,此时水合物完全分解。为进一步分析不同降压幅度下水合物分解损伤演化规律及其对产气规律的影响,选取0.45、0.91和1.8 MPa 3个降压幅度进行分析,如图3所示。

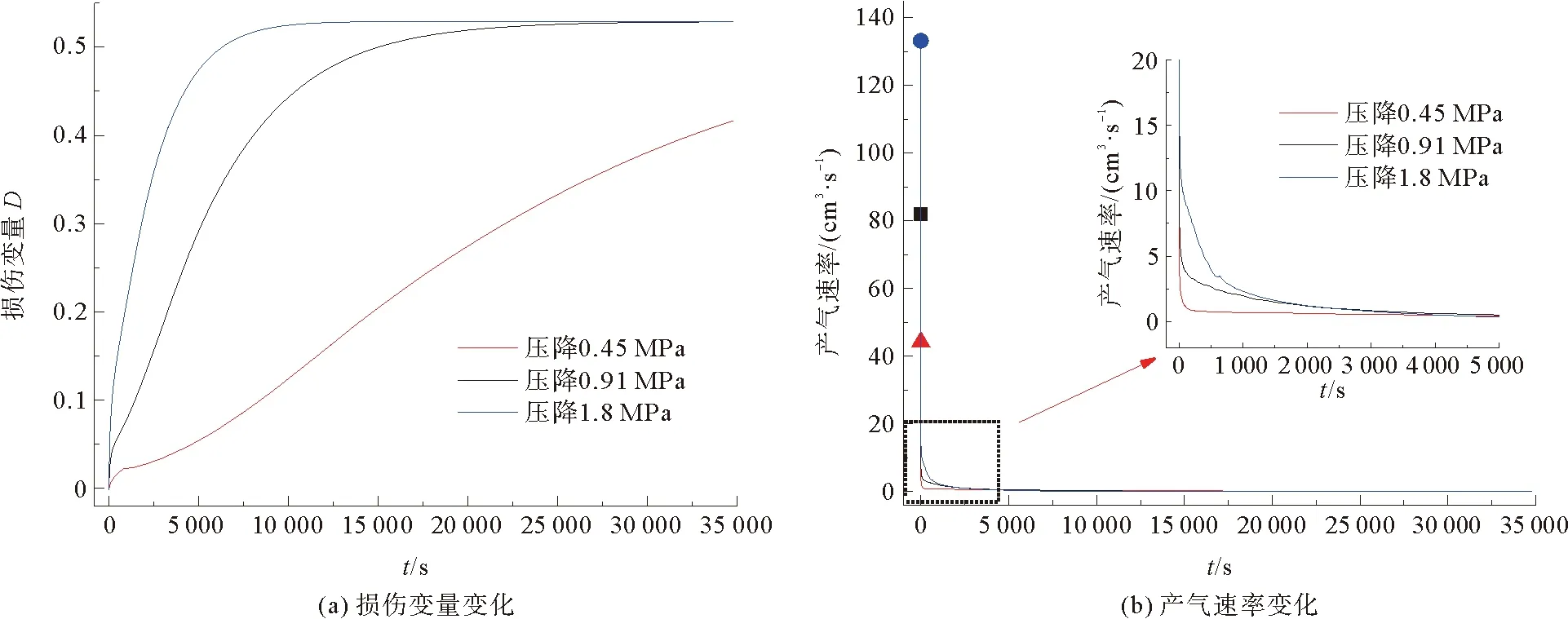
图3 不同降压幅度下水合物产气规律

在初始水合物饱和度为0.443,降压幅度为0.91和1.8 MPa时,损伤变量在天然气水合物分解35 000 s后达到最大值0.53,此时天然气水合物完全分解,如图3(a)所示。降压幅度较大,可提供较高的初始分解压力,水合物开始分解后,孔隙压力下降较快,有效应力迅速增加,此时承载压力的水合物逐渐减少,致使沉积物产生损伤,其整体弹性模量逐渐减小。随着有效应力不断增加,沉积物压缩变形进一步导致损伤加剧,使得产气通道迅速贯通。因此,在较大降压幅度下,水合物能够在较快的时间内完成分解,达到最终损伤状态。

降压开始后,产气速率瞬间达到峰值,然后迅速下降至较低的稳定产气速率,如图3(b)所示。突然降压导致降压端水合物迅速分解,产生分解损伤,孔隙度增大,产气速率较大,所以降压初期产气速率较大;随着水合物不断分解,沉积物在载荷作用下孔隙度减小,气体流动速度瞬间下降至较低稳定数值,产气速率也随之平稳,直至水合物完全分解。模拟结果显示,降压幅度为0.45 MPa时产气速率峰值为44.18 cm3/s,降压幅度为0.91 MPa时产气速率峰值为82.02 cm3/s,是降压幅度为0.45 MPa条件下产气速率峰值的1.86倍;降压幅度为1.8 MPa时产气速率峰值为133.17 cm3/s,是降压幅度为0.45 MPa条件下产气速率峰值的3.01倍。说明降压幅度越小时分解速度越慢,完全分解所需时间越长。

3.2 不同初始绝对渗透率影响分析

渗透率是评价流体通过多孔介质能力的基本指标,初始绝对渗透率是多孔介质在水合物饱和度为0时的绝对渗透率,表征多孔介质本身的渗透能力。为进一步探究不同初始绝对渗透率下水合物分解损伤演化规律及其对产气规律的影响,选取49、98和196 mD 3个不同初始绝对渗透率进行对比分析,如图4所示。

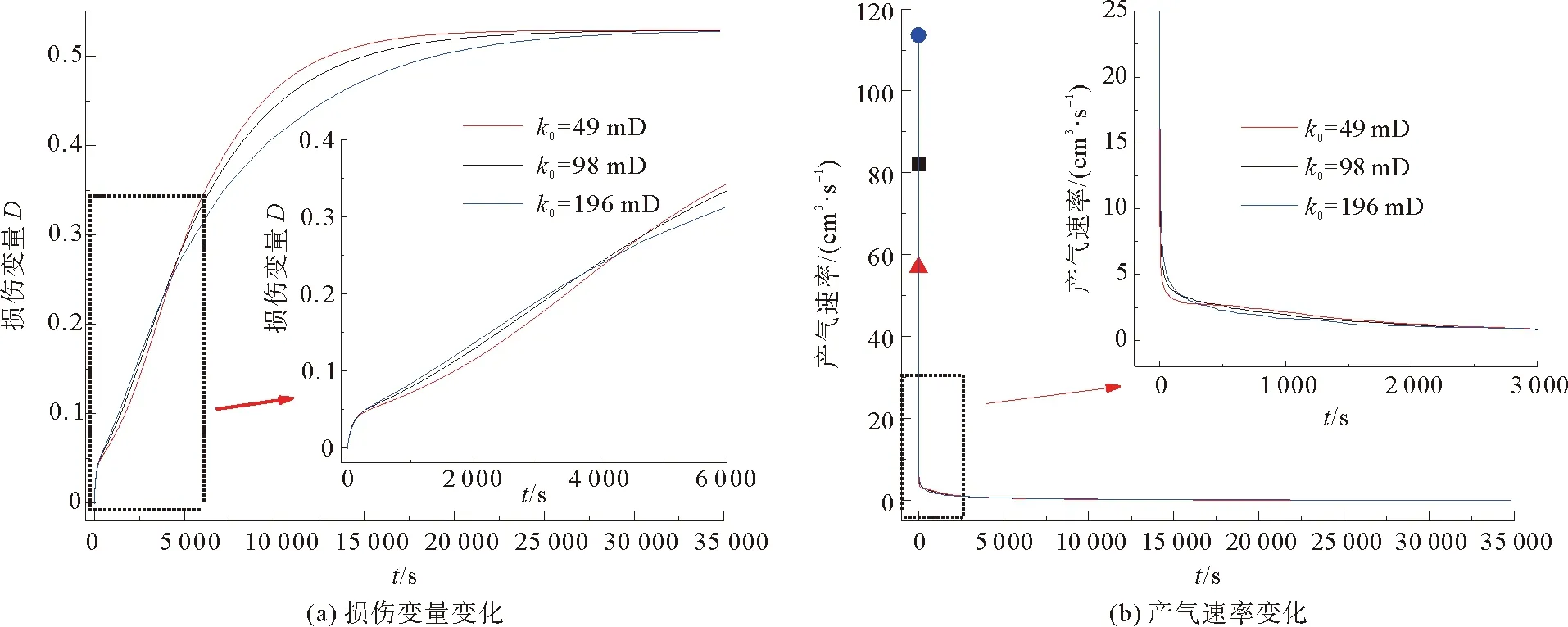
图4 不同初始绝对渗透率下水合物产气规律

水合物分解初期,损伤迅速产生,随着水合物继续分解,初始绝对渗透率为196 mD时,损伤最大,如图4(a)所示。这是由于在高初始绝对渗透率下,水合物分解产生的气体更易流出,初始分解速率最快,加剧损伤产生。当水合物进一步分解,绝对初始渗透率为49 mD时,损伤变量最快达到极限损伤,说明水合物最先达到完全分解状态。这是由于水合物的进一步分解引起有效应力迅速增大,在相同围压下水合物在高初始绝对渗透率下产生的压缩变形更大,从而导致孔隙闭合及产气通道关闭,抑制了水合物分解,损伤速率变缓。而低绝对初始渗透率模型虽然初始分解速率小,但分解过程中沉积物的压缩变形也较小,对产气通道的影响较弱,水合物在较快的分解速率和较小的压缩变形下损伤加快产生。

不同初始绝对渗透率下产气规律如图4(b)所示,降压分解后,产气速率瞬间达到峰值,且初始绝对渗透率越大,产气速率的峰值随之增大,初始绝对渗透率为98和196 mD时的产气速率峰值分别是初始绝对渗透率为49 mD时的1.44和1.99倍。初始绝对渗透率越高,产气初期损伤产生越快,气体在沉积物中更易流动,产气速率较快。进一步分解时,较高初始绝对渗透率下损伤受到的抑制作用越明显,水合物分解速率相对缓慢,产气速率较慢,因此较低的初始绝对渗透率下水合物更快达到完全分解。

3.3 不同初始孔隙度影响分析

初始孔隙度是多孔介质不含水合物时的初始孔隙度,并与水合物反应比表面积成正比。为进一步探究不同初始孔隙度下水合物分解损伤演化规律及其对产气规律的影响,选取不同初始孔隙度进行对比分析,如图5所示。

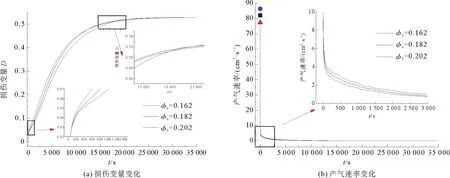
图5 不同初始孔隙度下水合物产气规律

天然气水合物分解35 000 s后,初始孔隙度为0.162、0.182和0.202时,天然气水合物完全分解,损伤变量达到最大值,初始孔隙度对损伤的影响呈现“快-慢-快”的3阶段,如图5(a)所示。降压后极短时间内,损伤随初始孔隙度增大而增大,但初始孔隙度对损伤的影响较小。最初的分解损伤会导致孔隙体积增大,因此较高的初始孔隙度促进损伤。分解一段时间后,较低初始孔隙度模型的损伤产生速率加快,这是因为失去了水合物颗粒的承载作用,沉积物有效应力增大,其压缩变形抑制水合物的快速分解,损伤较为缓慢。在产气后期,较高初始孔隙度模型的损伤速率逐渐加快,这是由于分解后期引起的沉积物变形量较小,而水合物不断分解使得沉积物中的孔隙体积持续增大,继续促进损伤产生,直至水合物沉积物达到最终损伤状态。因此经过“快-慢-快”3阶段后,高绝对初始孔隙度模型最终先达到完全损伤状态。不同初始孔隙度下产气速率如图5(b)所示,产气速率峰值随初始孔隙度的增大而增大,初始孔隙度为0.202和0.182时产气速率峰值分别比初始孔隙度为0.162时高11.72%和6.08%。较高的初始孔隙度增大了反应面积,损伤速率较快,并最先达到完全损伤,增大产气速率。

4 结论

建立了天然气水合物THMC全耦合降压开采模型,利用Masuda试验验证了模型的可靠性,并讨论了损伤效应的演化规律及其对产气规律的影响,得到以下结论。

1) 降压幅度大有助于产气。较大的降压幅度使得沉积物有效应力不断增大并加速沉积物损伤,产气初期水合物快速分解,产气速率较大,而后逐渐降低至较小的稳定产气速率。

2) 初始绝对渗透率越大,产气速率的峰值越大。高初始绝对渗透率在产气初期极短时间内加剧沉积物损伤,进一步分解时,在围压作用下沉积物产生较大压缩变形,抑制损伤产生,产气速率变慢,从而导致高初始绝对渗透率下的天然气水合物完全分解所需的时间较长。

3) 峰值产气速率随初始孔隙度的增大而增大。水合物分解效应对孔隙度的影响大于压缩变形对孔隙度的影响时,加速损伤,反之损伤被抑制,初始孔隙度对损伤的影响规律呈现出“快-慢-快”3个阶段,即分解初期较大孔隙度下分解速率较快,促进损伤产生;分解至中期时,在应力场作用下较大孔隙度产生较大压缩变形,抑制损伤产生;分解至后期时,较大孔隙度下水合物分解产生的孔隙体积大于沉积物压缩变形体积,使得损伤速率再次加快。