基于对偶神经网络的固体火箭发动机药柱非线性粘弹性力学分析方法①

贺 云,李海滨,杜 娟

(1.内蒙古农业大学 水利与土木建筑工程学院,呼和浩特 010018; 2.内蒙古工业大学 理学院,呼和浩特 010051;3.内蒙古财经大学 统计与数学学院,呼和浩特 010070)

0 引言

对于固体火箭发动机药柱粘弹性理论,国内外学者都进行了大量研究。在国外,CHARLES系统描述了固体推进剂粘弹性表征[1];JUNG等提出了一种考虑大变形及循环载荷对发动机装药影响的非线性本构方程[2];HIMANSHU等提出固体推进剂Maxwell模型,可以准确预测推进剂材料系数[3]。在国内,张海联等建立Lagrangian法随机虚功方程,研究了药柱的具有随机参数结构响应问题[4];张书俊等对固体发动机药柱进行粘弹性动态可靠度分析与不可压缩粘弹性随机有限元分析[5];张建伟等通过局部平均方法对随机场进行离散,得到随机粘弹性有限元方程[6];田四朋根据Herrmann变分原理和对应原理出发,推导得到了不可压和近似不可压粘弹性材料积分型本构关系[7];职世君根据药柱在固化降温情况下的结构完整性分析,在药柱施加点火冲击的压力载荷时,分别进行动态和准静态计算,得出较好的结果[8]。

综上所述,对于固体火箭发动机药柱粘弹性结构的力学性能分析,在线性粘弹性理论中对应原理分析方法较为成熟,是一种行之有效的方法,可以大大简化粘弹性问题的求解过程[9-14],但是对于非线性问题往往更贴近药柱实际情况。关于非线性粘弹性力学问题的研究,工程中应用较早的半经验单积分方法主要有四类,分别为修正的叠加方法[15]、Beinstin弹性流体理论[16]、Schapery热力学方法[17]及Valanis内时理论[18]。但这些方法模型中涉及较多需要待定的参数,本构关系复杂,给工程实际应用带来困难。SCHAPERY提出了一个基于伪应力和伪应变的对应原理,通过遗传性积分化,将现时应力和现时应变转换为伪应力和伪应变,给出了服从非线性弹性关系的伪应力和伪应变,但伪应力和伪应变的所有加载曲线不能完全重合,且卸载过程不能同时回到原点,不符合弹性力学性能要求[19-20]。胡强等提出基于多重积分的粘弹性本构关系及多重Laplace变换对应原理[21],但由于本构关系包含太多材料参数函数,很难解决实际问题。

神经网络作为在结构分析等领域被广泛应用的力学分析方法,同样在粘弹性研究方面也有涉及。ZHANG等进行了基于神经网络的短碳纤维增强复合材料聚四氟乙烯(PTFE)动态力学性能预测研究[22]。陈国荣在三元件粘弹性力学模型基础上,利用BP神经网路方法对地下洞室围岩粘弹性材料参数进行反分析[23]。伍振志等提出了利用遗传的神经网络算法进行粘弹性岩体力学参数反演[24]。TAO等基于分数阶导数模型分析了粘弹性材料的粘弹性特性,通过建立BP神经网络,实现了粘弹性参数的准确识别,从而分析了粘弹性材料的动态特性[25]。ZOPF等通过引入浅层神经网络,实现了弹性本构关系的准确描述,对于无法用模型表示的粘弹性材料,通过循环神经网络的深度学习,获得了粘弹性本构关系的准确表达,以天然橡胶为例,取得了良好的结果[26]。DEVRIES等通过一类深层神经网络的深度学习,得到了在任何时间及位置的流变学结构中粘弹性问题的有效解决方案,使得神经网络计算快速、可靠及具有高空间和时间分辨率,从而实现了大型粘弹性地震周期模型的计算[27]。

基于此,本文通过对应原理把粘弹性问题对应为弹性问题,在弹性力学问题解析求解方法的基础上,针对固体火箭发动机点火工作状态下,拟提出利用对偶神经网络方法求解管形药柱粘弹性力学问题新方法。

1 非线性粘弹性问题及其求解

1.1 非线性粘弹性本构关系

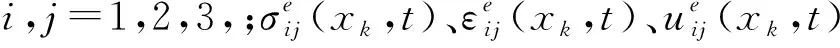
非线性粘弹性本构关系在一维情况下的Volterra-Frechet展开关系式可写为

(1)

参照Rabotnov[28],设Ji为i个不同变量的类函数乘积:

(2)

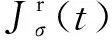
ε(t)=a1σe(t)+a2[σe(t)]2+a3[σe(t)]3+…

(3)

进而式(3)的反函数,即瞬时弹性应力可以表示为现时应变的函数为

σe(t)=φ[ε(t)]

(4)

1.2 非线性粘弹性对应原理

在小变形范围内,基于非线性本构关系找到一种非线性粘弹性对应原理。

平衡方程:

σij,j+Fi=0

(5)

几何方程:

(6)

本构关系:

(7)

或

(8)

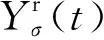
当边界条件为给定位移边界时,在边界s1上的面力及在边界s2上的位移分别为

(σijnj)s1=Ti=0

(9)

(ui)s2=Ui

(10)

式中nj为边界面外法线方向余弦。

物体内部体力Ti=0时,该粘弹性问题的解为

(11)

(12)

(13)

当边界条件为给定应力边界时,在边界s1上的面力及在边界s2上的位移分别为

(σijnj)s1=Ti

(14)

(ui)s2=Ui=0

(15)

则该粘弹性问题的解为

(16)

(17)

(18)

2 对偶神经网络方法求解弹性力学平面问题

2.1 弹性力学平面问题的偏微分方程描述

根据弹性理论可知,弹性力学平面问题可以归结为含有边界条件的偏微分方程求解[31]。

对于弹性力学平面问题,按应力求解时,得到直角坐标系下的相容方程:

(19)

式中φ为应力函数。

假设边界条件全部为应力边界条件,则在边界s上有如下表达式:

(20)

(21)

同理,根据弹性力学理论,极坐标系下相容方程可表示为

(22)

应力边界条件为

(23)

(24)

2.2 应力函数的对偶神经网络解法

将坐标变量x、y和应力函数φ(x,y)的关系式写为如下神经网络形式:

(25)

式中ki1、ki2为输入层到隐层单元连接权值;bi为隐层单元阈值;wi为隐层到输出层单元连接权值;c为输出层单元阈值。

针对式(19)、式(25)对坐标变量求偏导可得下列式(26)～式(28)。

(26)

(27)

(28)

文献[32]指出隐层单元激活函数为exp时,较logsig、tansig等传统激活函数,同样具有很好的泛化能力。为了方便构造神经网络之间的求导关系,本文方法网络隐层单元激活函数选取为f(x)=ex。将式(26)～式(28)代入式(19)等式左端,可得神经网络形式为

f(ki1x+ki2y+bi)=h1(x,y)

(29)

在弹性理论中,结构除必须满足式(29)控制方程之外,对于具体问题,还需满足相应的边界条件,然后根据方程给出其神经网络形式。

不计体力,根据应力函数φ可以得到应力分量:

(30)

(31)

将式(30)～式(32)带入边界条件式(20)、式(21)中,得到对应的神经网络形式:

式(29)、式(33)、式(34)就构成了弹性力学问题的神经网络求解表达式。

2.2.1 神经网络结构

比较式(29)、式(33)与式(34),各网络具有相同的结构,为双输入、单输出、n个隐层单元的前馈型神经网络,如图1所示。

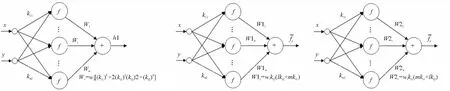
(a) Eq.(29) (b)Eq.(33) (c)Eq.(34)图1 式(29)、式(33)、式(34)对应神经网络结构Fig.1 Neural network structure of Eq.(29), Eq.(33) and Eq.(34)

Wi=wi[(ki1)4+2(ki1)2(ki2)2+(ki2)4]

W1i=wiki2(lki2+mki1)

W2i=wiki1(mki1+lki2)

运用多神经网络联合训练算法对上述神经网络系统进行联合训练,训练后的网络参数ki1、ki2、bi、wi带入式(30)～式(32),得到应力分量的神经网络数值解。

2.2.2 多神经网络联合训练算法

(35)

其中,

f(ki1x+ki2y+bi)-h1(x,y)

因此,结合L-M训练算法,多神经网络联合训练算法的计算步骤如下:

(1)初始化网络参数,得到训练误差e、常数μ0和学习率μ的增加率β(0<β<1),令迭代步数r=1,μ=μ0。

(3)计算雅可比矩阵J(xr)、梯度矩阵g(xr)、拟海瑟矩阵H(xr)。

(4)根据L-M训练算法中的迭代算式Δx=-[H(xr)+μI]-1g(xr),计算权值、阈值的变化矩阵Δx。

3 管形药柱非线性粘弹性力学分析

固体火箭发动机点火工作状态下,其药柱的粘弹性特性对振动情况有影响,所以不能忽视。由于固体火箭发动机药柱呈现出粘弹非线性,所以对其进行非线性粘弹性力学分析是必要的。

固体火箭发动机截面可简化为图2的形式[33]。管形药柱为粘弹特性的推进剂,内径a=0.12 m,外径b=0.2 m。壳体为线弹性钢壳,厚度为δ1=0.003 m。如考虑壳体为线弹性材料,药柱及壳体的相关参数为药柱瞬态弹性模量E(0)=5.5766 MPa,药柱泊松比μ=0.489,药柱密度ρ=1635.2 kg/m3;壳体弹性模量Ec=196.5 GPa,壳体泊松比μc=0.29,壳体密度ρc=7850 kg/m3。设发动机圆筒段长L=3 mm,粘弹性材料的材料阻尼c=0.01,总体结构瑞利阻尼阻尼系数为0.000 5。

图2 发动机截面简图Fig.2 Simplified cross section of solid rocket motor

在点火状态下,发动机工作时其圆筒段处于无约束状态且无预应力等影响。由于药柱在燃烧时的强大气流对内壁产生压力,所以分析内压作用下药柱的力学行为较为贴合实际情况。根据文献[34],载荷q(t)是关于时间的渐变函数,关系式为

q(t)=mp0[1-exp(-nt)]

(36)

式中p0为渐变载荷幅值,p0=2.0 MPa;m、n为系数,m=1,n=0.4;t为发动机工作时刻,t=1,2,3,…,30 s。

3.1 对偶神经网络方法求解瞬时应力分量

当边界条件为应力边界时,得到粘弹性应力分量的解为式(17),现时应力和瞬时应力相等。根据文献[29]中关于粘弹性材料应力、应变关系的阐述,粘弹性材料的瞬时应力、应变分量服从弹性力学的规律,上述粘弹性力学问题可以转换为弹性力学问题。这样就可以通过对偶神经网络对弹性力学的求解方法进行数值求解。由于考虑壳体的影响,药柱和壳体的材料性质不同,不符合均匀性假设,必须考虑交界面的接触条件,由多连体的位移单值条件,取药柱的应力表达式为

壳体的应力表达式为

并考虑边界条件和接触条件,注意到这里是平面应变问题,药柱和壳体的径向位移表达式为

在接触面上,药柱和壳体具有相同的位移:

φ取任何数值时,上式均成立。

通过以上条件,得到待定常数A、C、A′、C′,得到ρ=b处的径向应力边界条件为

(37)

其中,

根据弹性力学应力求解相容方程可写为

(38)

补充的边界条件有

(τρφ)ρ=a=0,(τρφ)ρ=b=0

(39)

(σρ)ρ=a=-q(t)

(40)

将极坐标系下应力函数的神经网络形式带入相容性方程及边界条件,由于边界条件式(39)自动满足,所以只需构造式(37)、式(38)及式(40)对应的神经网络。两个网络都为单输入、单输出、三层前馈型神经网络。如表1所示,药柱半径为[0.12,0.2]范围内均匀取9个点作为神经网络训练输入样本,表1中y1和y2分别为相容方程式(38)和边界条件式(37)、式(40)所对应的网络输出。

表1 神经网络系统训练样本Table 1 Neural network system training samples

算例中隐层单元个数n=10,运用多神经网络联合训练算法训练网络系统100步,t=1 s时误差收敛曲线如图3所示。

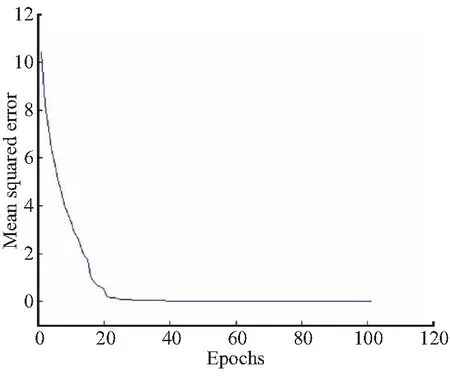
图3 网络系统误差收敛曲线Fig.3 Error convergence curve of network systems

针对不同的时间t对应的渐变载荷q(t),神经网络方法循环计算30次,得到t=1,2,3,…,30 s时的危险点药柱内表面瞬时应力分量,如图4所示。

(a) Instantaneous radial stress (b) Instantaneous hoop stress图4 瞬时应力随时间的变化曲线Fig.4 Curves of instantaneous stress with time varies

3.2 本构关系的推导

根据Stieltjes卷积的交换律及Gurtin和Sternberg的处理方法,式(17)可以写为

(40)

根据粘弹性理论相对松弛模量计算方法,得到相对蠕变柔量的表达式为

(41)

进而

(42)

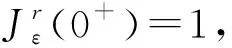
(43)

由于粘弹性材料的瞬时应力、应变分量服从弹性力学规律,所以瞬时应变分量可以写为

(44)

(45)

根据文献[35],固体火箭发动机药柱粘弹性材料泊松比可以用自定义神经网络通过如下拟合表达式进行拟合,且拟合效果较好。

(46)

拟合表达式中各参数如表2所示,拟合曲线如图5所示。

表2 泊松比拟合表达式中各参数Table 2 The parameters in Poisson 's fitting expression

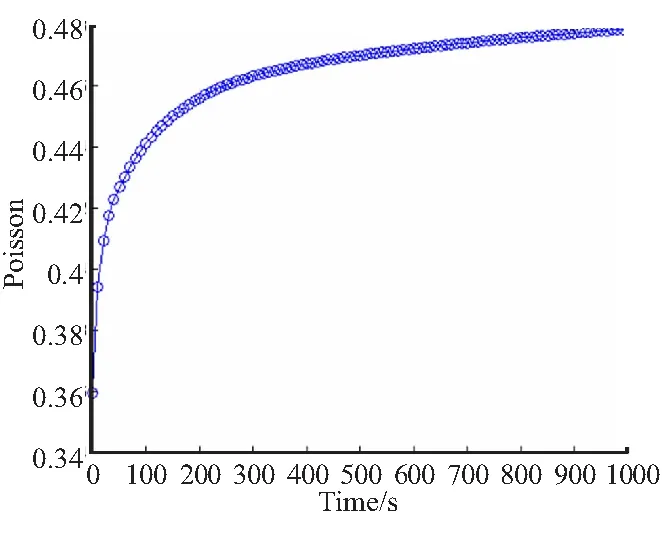
图5 泊松比拟合曲线Fig.5 Poisson 's fitting curve

这样,式(44)中的所有参量都可以得到,进而瞬时径向应变就可以写为

(47)

根据式(43)、式(47)、式(48),得到现时径向应变的表达式为

(49)

同理,也可以得到现时环向应变的表达式。

3.3 结果分析

根据对偶神经网络构造及积分方法,计算现时应变分量表达式中的积分项,从而得到现时应变分量随时间变化的曲线如图6所示,对应的现时应力-应变曲线如图7所示。

(a) Current radial strain (b)Current hoop strain图6 现时应变随时间的变化曲线Fig.6 Curves of current strain with time varies

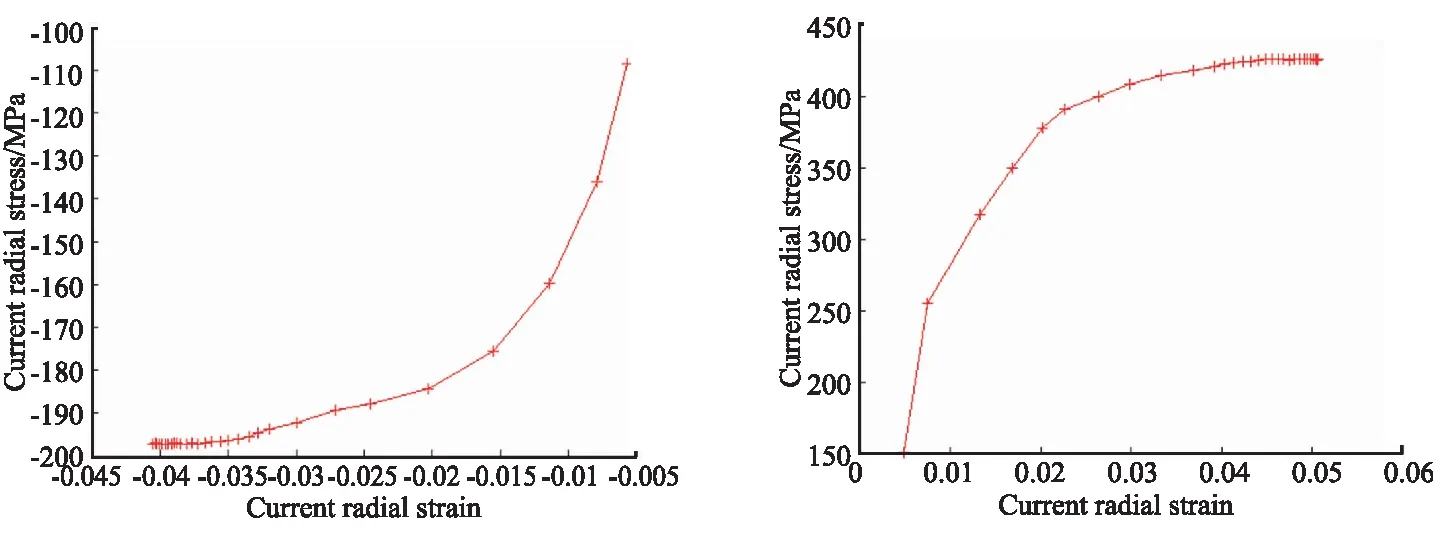
(a) Current radial stress-strain (b) Current hoop stress-strain图7 现时应力-应变曲线Fig.7 Current stress-strain curves

为了验证方法的有效性,作为对比对圆筒进行有限元仿真, 根据对称性选取结构的1/4,划分1400个单元格,如图8所示。

图8 有限元网格划分及观测点Fig.8 Finite element mesh division and observation points

同样选取式(36)渐变载荷幅值p0=2.0 MPa,m=1,n=0.4。首先,渐变载荷历时30 s,观察药柱响应随时间的变化规律;然后,卸掉载荷再观察药柱的30 s回复过程。选取4项Prony级数拟合模量函数,有限元仿真模拟得到1～30 s时刻位移,图9为30 s时的径向位移云图。

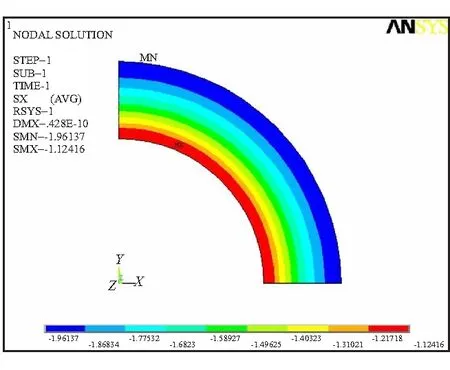
图9 30 s时的径向位移云图Fig.9 Radial displacement contour of the grain at 30 s

从图9看出,圆筒内径处位移最大。由于药柱内表面不能产生过大形变是压力载荷下药柱的失效判据,即药柱危险点处径向最大位移应当小于其极限位移,所以取内径处的径向应变作为对比。表3为本文方法与有限元方法结果对比。从表3中可看出,以划分1400个单元格的有限元方法作为理论解,本文方法体现出很好的精度,最大相对误差为 2.941 2%,符合工程实际<5%的要求。而当有限元方法划分20个单元格时,最大相对误差达到7.202 2%。在计算效率方面,本文方法优于有限元方法,有限元方法划分1400个单元格,而本文对偶神经网络仅训练100步,体现出较好的计算效率。

表3 1～30 s危险点处径向应变结果对比Table 3 Comparison of radial strain results at the danger point 1～30 s

4 结论

本文给出了一种基于对偶神经网络的固体火箭发动机药柱非线性粘弹性力学分析方法,通过对发动机药柱的简化模型进行粘弹性力学分析,根据对应原理及对偶神经网络方法,得到了该算例模型各点处的现时应力、应变分量,由于粘弹性材料内部恢复力的存在,现时径向应变分量随时间的增加逐渐减小,现时环向应变分量随时间的增加逐渐增大,这符合粘弹性材料的规律。

由于药柱内表面不能产生过大形变是药柱的失效判据,所以作为对比,采用本文方法和有限元方法同时分析圆筒内径处的径向位移,得到1～30 s时的计算结果,以划分1400个单元格的有限元方法作为理论解,本文方法的最大相对误差为2.941 2%,符合工程实际要求。

有限元收敛的标准为:单元越多,精度越高,越接近精确解,而计算过程中不能达到无数多个单元,所以只能越来越接近精确解。有限元软件一般采用位移法有限元,需要进行应力修匀,在网格较少的情况下,传统的应力修匀方法在边界处的应力误差很大,本文固体火箭发动机药柱模型危险点恰处于内边缘处,从而使有限元方法计算受到局限。神经网络方法计算体现出较好的优势,网络训练步数较少,而在边界处计算精度可以保障,不受应力修匀的影响,从而在保证计算精度的情况下,本文方法的计算效率优于有限元方法。

本文贡献在于:(1)在粘弹性力学分析中,将应力函数写成神经网络表达式,无需根据问题的不同假设不同的应力函数,克服了应力函数的分析困难;(2)由于本文神经网络方法直接从理论求解粘弹性力学问题的偏微分方程出发,所以相比传统有限元方法的求解过程,本文方法无需对粘弹性体物理模型进行网格划分;(3)通过本文方法的求解,使粘弹性力学问题的数值解具有良好的计算精度和效率,对固体火箭发动机粘弹性体力学分析提供了一种新的思路。

同时,可以通过本文方法对模型中所有点进行力学分析,从中找出危险点,为分析固体火箭发动机药柱可靠性提供条件。