喉栓式固体轨控发动机单阀推力偏差不确定性分析①

张德权,贾军凯,武泽平,王东辉,牛 禄,周伟华

(1.河北工业大学 机械工程学院,天津 300401;2.国防科技大学 空天科学学院,长沙 410073;3.上海航天动力技术研究所,上海 201109)

0 引言

固体姿轨控发动机(Solid Divert and Attitude Control Motor,SDACM)可以为飞行器轨道和姿态调整提供动力[1]。其工作原理是通过改变喉栓位移以控制阀门燃气流量,从而调节单阀推力大小,进一步通过多个单阀推力合成不同大小和方向的合推力矢量,实现飞行器轨道和姿态控制[2]。固体姿轨控发动机中各种不确定性因素相互耦合,引起实际推力与名义推力之间的偏差,导致飞行器轨道和姿态难以达到预期控制效果[3]。为此,对固体姿轨控发动机推力偏差进行不确定性分析,研究推力调控过程中不确定性因素传递规律,为固体姿轨控发动机实现快速准确调控提供参考。

目前,研究发动机推力性能主要手段是计算流体力学(Computational Fluid Dynamics,CFD)和有限元分析等数值模拟方法[4],但是这些方法求解成本高,计算效率低。为此,代理模型方法被引入到固体发动机性能研究中以提高计算效率。代理模型仅需少量的仿真样本就可以将原有复杂耗时仿真模型替换为简单数学模型,显著降低计算成本[5]。常用的代理模型有径向基函数[6]、响应面模型[7]和Kriging模型等[8]。多位学者将代理模型方法用于构建固体发动机近似模型以降低计算成本。文谦等[9]使用径向基函数模型对运载火箭进行气动力和结构承载能力近似建模,大幅提高计算效率。TOLA等[10]通过响应面模型研究几何参数与火箭发动机结构完整性和内弹道性能之间的关系。王鹏宇等[11]采用基于Kriging模型的优化框架,实现多工况下喉栓式固体发动机喷管型面优化设计。

上述研究均从确定性角度出发分析固体发动机性能,未考虑固体发动机中的不确定性因素[12],为此,多位学者[13-16]考虑环境载荷、材料属性和结构尺寸等多源不确定性因素对发动机药柱贮存、药柱结构和密封性能的不确定性进行分析。然而,固体姿轨控发动机推力性能不确定性相关研究还较为少见。固体姿轨控发动机推力性能同样受到多源不确定性因素影响,主要包括伺服机构不确定性、加工精度不确定性以及推进剂材料属性不确定性等。这些不确定性因素导致发动机推力实际值与名义值存在偏差,如果推力偏差超出控制系统容许偏差,会导致固体姿轨控发动机难以达到预期轨道控制效果。因此,考虑固体姿轨控发动机中推力影响因素的不确定性,对推力偏差进行不确定性分析具有重要意义。

本文采用Fluent进行固体轨控发动机单阀推力仿真计算获取名义推力。然后,考虑参数不确定性进行仿真计算,得到轨控发动机单阀仿真推力样本。根据仿真推力样本和名义推力建立轨控发动机单阀推力偏差Kriging模型,实现推力快速预测。在推力偏差Kriging模型基础上,对其进行不确定性分析,获取轨控发动机单阀推力偏差概率曲线,并计算不同容许偏差下推力偏差可靠度。基于代理模型对固体姿轨控发动机推力偏差进行不确定性分析,有望为快速量化评估实时调节过程的推力输出不确定性提供参考,同时对固体姿轨控发动机性能可靠性设计具有一定理论指导意义。

1 轨控发动机单阀推力建模

固体姿轨控发动机一般由姿控发动机和轨控发动机组成,其中姿控发动机为飞行器姿态控制提供动力,轨控发动机实现飞行器轨道变换。在轨控发动机工作过程中,通过多阀协同调节,控制各阀门推力,可以合成不同大小和方向的合推力矢量,实现飞行器姿态和轨道控制。因此,轨控发动机推力快速精确调节是实现飞行器高精度目标控制的基础[17],若实际推力与名义推力间的偏差超过控制系统容许偏差,会导致固体姿轨控发动机脱离预定轨道,无法完成预期任务。

1.1 轨控发动机单阀推力计算模型

轨控发动机单阀推力计算公式为[18]

(1)

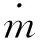
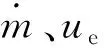
(2)

式中ρ为推进剂密度;C*为特征速度;a为燃速系数;Ab为药柱燃面面积;At为喷管等效喉部面积;n为压强指数。

由式(2)可以看出,燃烧室压强主要受到推进剂材料属性、装药尺寸和等效喉部面积三方面因素影响。因此,分别从三方面选取共计六种影响因素对喉栓式固体轨控发动机单阀推力进行分析计算。推进剂材料属性相关因素为随机性较强的推进剂特征速度和推进剂密度;由于采用端面燃烧装药,装药尺寸方面选择药柱直径;等效喉部面积影响因素有喉栓位移、喉栓直径和喷管喉径。六种影响因素信息列于表1。

表1 轨控发动机单阀推力影响参数Table 1 Influence parameters of single valve thrust in the divert motor

计算得到燃烧室压强后,需要对固体轨控发动机进行内流场仿真,进而根据仿真结果计算发动机推力。图1为固体姿轨控发动机喷管构型及装药示意图。由于喉栓和喷管均为回转体,为此采用二维轴对称原理简化喷管构型以提高计算效率。简化后喷管构型如图2所示。

图1 轨控发动机喷管构型及装药示意图Fig.1 Nozzle configuration and propellant charging schematic of divert motor

图2 轨控发动机简化喷管构型Fig.2 Simplified nozzle configuration of divert motor

1.2 轨控发动机单阀推力内流场仿真方法

固体姿轨控发动机工作过程中流体满足连续介质假设,遵循流体力学基本方程:质量守恒方程、动量守恒方程和能量守恒方程[19]。因此,建立流体控制方程组[20]:

(1)连续方程

(3)

(2)动量方程

(4)

(3)能量方程

·uiτji+pujfj+SE

(5)

采用Realizablek-ε两方程湍流模型对湍动能k和耗散速度ε进行求解。仿真计算完成后,将结果代入式(1)即可计算获取仿真推力。

为验证本文仿真方法的准确性和有效性,建立文献[21]中喷管构型CFD仿真模型,分别与低压(4 MPa)和高压(12 MPa)两种不同工况的试验结果进行对比,结果如表2所示。高压状态喷管流场云图如图3所示。由表2可见,低压和高压状态下仿真推力与试验结果相对误差均在5%以内,表明本文所用数值仿真分析方法精度满足实际工程分析需求。

表2 仿真推力与试验推力结果对比[21-22]Table 2 Comparisons of simulation thrust and test thrust[21-22]

(a)Pressure contour

1.3 轨控发动机单阀推力仿真计算

喉栓式轨控发动机的燃烧室压强随喉栓位移变化,因此采用压力入口边界条件,总温为3200 K。喷管和喉栓等壁面采用绝热无滑移壁面边界条件,其型面根据输入条件可变化。将出口边界条件定义为压力出口,环境压强及温度设置为海平面标准大气参数。

计算域网格划分如图4所示。轨控发动机喷管及喉栓型面变化复杂,因此采用三角形非结构网格,并对物理量变化较剧烈的区域,如边界层、喷管喉部及喉栓头部等进行网格加密处理。

图4 喷管流场计算域网格Fig.4 Grid of calculation region of nozzle flow field

网格无关性验证结果列于表3。当网格数量达到55 223后,仿真推力计算结果受网格密度影响较小。因此本文计算域网格数量选择55 223,推力仿真结果云图如图5所示,计算得到仿真推力F0=7.863 5 kN。

表3 CFD仿真模型的网格无关性验证Table 3 Verification of grid-independence of the CFD simulation model

本文建立轨控发动机单阀推力计算模型,选择推力影响参数进行仿真计算。将计算推力作为名义推力,为轨控发动机单阀推力偏差代理模型构建提供基础仿真数据。

2 轨控发动机单阀推力偏差代理模型构建

不确定性分析需要足够多的仿真数据支撑以获得精确结果,而轨控发动机推力仿真单次耗时约为0.5 h,直接使用仿真模型进行不确定性分析会造成难以承受的计算负担。为此,通过少数仿真计算构建单阀推力偏差代理模型代替耗时仿真模型,以减少计算量。由于Kriging模型具有较为良好综合性能[23],本文选择Kriging模型近似轨控发动机单阀推力偏差。

2.1 Kriging模型原理

Kriging模型是基于随机过程的半参数化模型,可以实现空间分布参数的无偏估计,仅需估计点附近的局部信息就可以给出全局近似[23]。假设有n维样本x=[x1,x2,…,xn],其对应的响应值为Y=[Y1(x),Y2(x),…,Yn(x)],则Kriging模型一般形式可表示为[23]

g(x)=fT(x)β+z(x)

(6)

式中f(x)=[f1(x),f2(x),…,fm(x)]T为回归模型基函数;β=[β1,β2,…,βm]T为回归系数向量,m为基函数的个数;fT(x)β为线性回归部分;z(x)为均值为0、方差为σ的正态分布随机过程,表示模型对线性回归部分的局部随机偏差。

不同样本点之间的协方差由式(7)计算:

cov(z(xi),z(xj))=σ2Rθ(xi,xj)

(7)

式中i,j=1,2,…,n;Rθ(xi,xj)为样本点xi与xj之间的相关函数;θ为相关性参数。

根据最小二乘法,未知系数β和随机过程方差σ2可分别估计为[24]

(8)

(9)

式中F为由Fik=fk(xi)组成的矩阵(i=1,2,…,n;k=1,2,…,m);R为Ri,j=Rθ(xi,xj)组成的矩阵。

Kriging模型预测函数为

(10)

式中rT(x)=[R(x,x1),R(x,x2),…,R(x,xn)]。

2.2 轨控发动机单阀推力偏差Kriging模型构建

轨控发动机单阀推力受到喷管构型等几何尺寸以及推进剂属性影响,而这些因素不可避免地存在不确定性,将推力影响参数考虑为随机变量更加符合工程实际。因此,将表1中参数设定为服从正态分布的随机变量[20,25],则其概率分布信息列于表4。

表4 单阀推力不确定参数统计信息Table 4 Statistical data of uncertain parameters for the single valve thrust

考虑表4中随机变量,实际推力与名义推力之间的偏差ε可表示为

ε(x)=F(x)-F0

(11)

式中F(x)为轨控发动机单阀实际推力;x为随机输入参数组成的六维向量;F0为名义推力,根据轨控发动机单阀推力偏差仿真计算结果,取F0=7.863 5 kN。

推力Kriging预测值为

(12)

针对文中的六维问题,一次实验设计法采用60组初始样本可以构建较为精确的代理模型[26]。为保证轨控发动机单阀推力偏差代理模型的精度,根据表4所示推力影响因素统计信息生成110组随机样本,通过CFD获得仿真推力值,由输入参数和对应仿真推力组成110组样本,从中选取90组构建样本用以建立单阀推力偏差Kriging模型,20组测试样本来验证代理模型精度。

四种常用代理模型精度评价指标[23]分别为复相关系数(R2)、均方根误差(eRMSE)、相对平均绝对误差(eRAAE)和相对最大绝对误差(eRMAE),其表达式如下[27]:

(13)

(14)

(15)

(16)

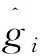
σSTD表达式为

(17)

四种评价指标中,eRMSE和eRAAE用于评估模型全局精度,其值越接近0表明模型全局精度越高;eRMAE用来评估模型局部精度,其值越接近0,模型局部精度越高;R2用于评估模型全局精度,其值越接近于1表明模型精度越高。20组测试样本上的评价指标值列于表5。

表5 单阀推力偏差Kriging模型精度评价指标Table 5 Evaluation index of Kriging model accuracy for single valve thrust deviation

由表5可知,所建立单阀推力偏差Kriging模型具有较高的全局精度,而其局部精度评价指标eRMAE值为0.935 2。为此,根据式(12)计算测试样本处推力Kriging预测值,与对应样本处CFD模拟值进行对比并求出相对误差,推力预测相对误差如图6所示。由图6可知,20组测试样本中仅2组样本推力预测值和模拟值的相对误差大于0.4%,说明所建立轨控发动机单阀推力偏差Kriging模型具有足够高的局部精度。

图6 Kriging预测推力和CFD模拟推力相对误差图Fig.6 Relative error of Kriging predicted thrust and CFD simulated thrust

本文考虑参数不确定性对轨控发动机单阀推力进行仿真计算,获得其偏差响应样本。使用随机输入参数和推力偏差响应样本构建推力偏差Kriging模型并验证其精度,数据表明,所建代理模型具有较高的全局精度和局部精度。

3 轨控发动机单阀推力性能分析

3.1 轨控发动机推力影响因素敏感性排序

为研究轨控发动机推力对各影响因素的敏感性,将各参数分别设为服从正态分布的随机变量,其他5个变量为固定值,通过单阀推力偏差的标准差度量推力对各影响参数变化的敏感程度。推力偏差的标准差越大,表示推力对相应随机参数的变化越敏感。当第k个因素为随机变量时,相应的轨控发动机单阀推力可表示为

(18)

式中χk=(μ1,…,μk-1,xk,μk+1,…,μ6),μk为第k个因素的均值,χk为第k个随机变量。

在建立的轨控发动机单阀推力偏差Kriging模型基础上,采用蒙特卡洛模拟法(MCS)获取推力偏差的标准差,计算结果列于表6。由表6可知,当取喉栓直径为随机变量时,推力偏差的标准差最大,达到0.016 3 kN。取药柱直径为随机变量时的推力偏差标准差最小,为0.000 8 kN。这表明,喉栓直径对轨控发动机单阀推力偏差不确定性水平的影响最大,而药柱直径则导致推力偏差的最低不确定性水平。

表6 不同不确定变量下推力偏差的标准差计算结果Table 6 Results of standard deviation for thrust deviation with different uncertain parameters

为更加直观地比较各参数对推力偏差的影响,图7给出推力偏差敏感性分析结果柱状图。可知,各参数对推力影响程度排序:喉栓直径>喉栓位移>喷管喉径>推进剂密度>推进剂特征速度>药柱直径。

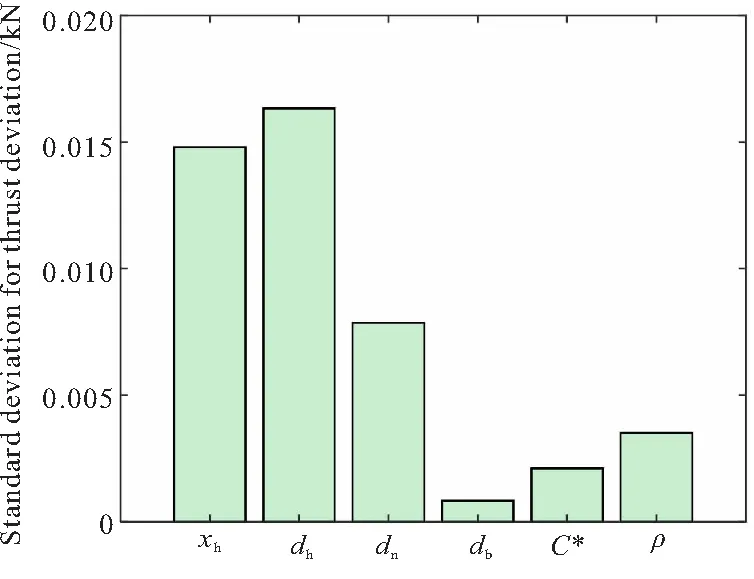
图7 推力偏差敏感性结果Fig.7 Sensitivity result of thrust deviation

由于等效喉部面积Ar对燃烧室压强pc和固体轨控发动机推力都存在影响,表明等效喉部面积不确定性对推力不确定性影响效果更显著。六种推力影响因素中,喉栓直径、喉栓位移和喷管喉径三因素与等效喉部面积相关,推进剂密度、推进剂特征速度和药柱直径三参数与燃烧室压强相关。因此,喉栓直径、喉栓位移和喷管喉径对推力偏差影响程度大于推进剂密度,推进剂特征速度和药柱直径对推力偏差影响程度。

3.2 轨控发动机单阀推力偏差不确定性分析

表7给出了考虑参数不确定性时110组CFD模拟推力和105组Kriging预测推力最大值、最小值和平均值。

表7 考虑参数不确定性的轨控发动机单阀推力值Table 7 Single valve thrust values of divert motor considering parameter uncertainties

由表7可知,考虑不确定性的推力值和推力名义值相比有较大波动范围,表明固体姿轨控发动机推力影响因素的不确定性对推力性能有不容忽视的影响。因此,需要开展轨控发动机单阀推力偏差不确定性分析,进一步探明参数不确定性对固体姿轨控发动机推力性能的影响规律。

在轨控发动机单阀推力偏差Kriging模型的基础上,采用MCS方法对轨控发动机单阀推力偏差进行不确定性分析。110组CFD模拟推力偏差和105组Kriging预测推力偏差的前两阶矩列于表8。

表8 轨控发动机单阀推力偏差前两阶矩Table 8 The first-two order moments for single valve thrust deviation of divert motor

由于CFD数值模拟的样本量限制,其结果仅具有一定的参考意义。两种方法得到的推力偏差均值和标准差都相差不大,说明Kriging预测推力偏差不确定性分析结果精度较高。

图8为轨控发动机单阀推力偏差概率密度函数(Probability Density Function,PDF)和累积分布函数(Cumulative Distribution Function,CDF)曲线。由图8可知,在整体趋势上,Kriging预测值的概率曲线和CFD仿真值概率曲线拟合较好。出于计算成本考虑,本文仅获取110组CFD模拟数据,难以获得准确推力偏差概率信息,导致其PDF和CDF曲线有较大波动。因此,以105组样本所得Kriging预测值的概率曲线分析固体轨控发动机单阀推力偏差不确定性。

(a)PDF curves of the thrust deviation

(b)CDF curves of the thrust deviation图8 轨控发动机单阀推力偏差概率曲线Fig.8 Probability curves of single valve thrust deviation for divert motor

当轨控发动机实际推力与名义推力之间偏差小于一定范围时,可由控制系统对其推力进行补偿,以保证发动机实现预期轨道控制效果,此范围称为控制系统容许偏差。当推力偏差小于容许偏差时,认为轨控发动机推力偏差性能可靠[25]轨控发动机推力偏差性能可靠的概率称为轨控发动机推力偏差可靠度。

表9为容许偏差分别取0.01～0.1 kN时的推力偏差可靠度。当容许偏差取0.1 kN时,推力偏差CFD仿真值与Kriging预测值的可靠度分别为99.12%和99.56%,表明此时固体姿轨控发动机控制系统可以补偿几乎全部推力偏差,使其达到理想控制效果。当轨控发动机单阀推力偏差可靠度设计要求为99%时,控制系统对发动机推力输出的容许偏差为0.09 kN即可实现该设计要求。

表9 不同容许偏差下单阀推力偏差可靠度Table 9 Reliability of single valve thrust deviation subject to different tolerable deviations

为更直观地比较不同容许偏差下轨控发动机单阀推力偏差可靠度,图9给出对应到单阀推力偏差PDF曲线上的推力偏差可靠域,其中灰色区域面积表示单阀推力偏差可靠度。

(a)Tolerable deviations is 0.02 kN

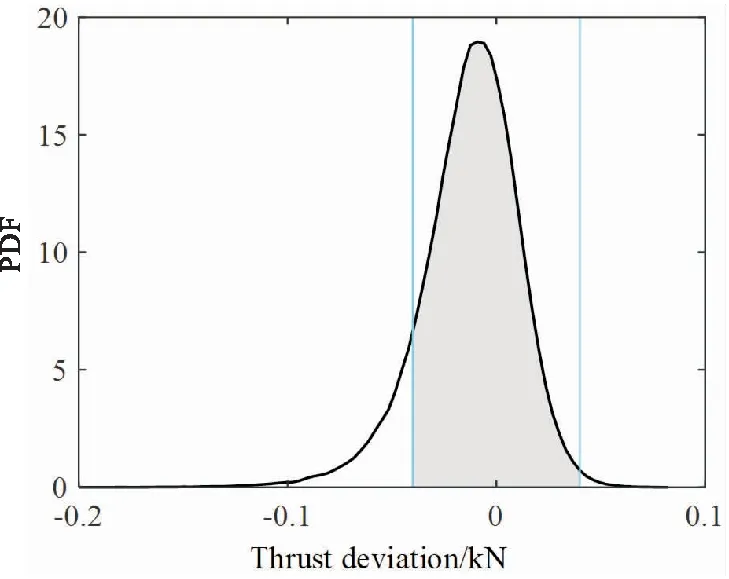
(b)Tolerable deviations is 0.04 kN

(c)Tolerable deviations is 0.06 kN图9 不同容许偏差下单阀推力偏差可靠域Fig.9 Reliability region of single valve thrust deviation subject to different tolerable deviations

对固体轨控发动机推力偏差进行不确定性分析,探明发动机推力调控过程中参数不确定性的影响,可为固体姿轨控发动机推力快速准确调节提供参考。同时,可以更加高效并直观地了解该发动机推力性能是否满足可靠性设计要求,为喉栓式固体轨控发动机设计提供理论指导。

4 结论

考虑影响固体姿轨控发动机推力性能的不确定性因素,基于CFD数值模拟构建轨控发动机单阀推力偏差Kriging模型,探究不确定性对固体姿轨控发动机推力偏差的影响。主要结论如下:

(1)根据轨控发动机推力调控原理和计算模型,将喉栓位移、喉栓直径、喷管喉径、药柱直径、推进剂密度和特征速度等参数的不确定性视为影响轨控发动机推力性能的主要因素。

(2)采用复相关系数、均方根误差、相对平均绝对误差和相对最大绝对误差四种评价指标对本文构建的代理模型进行精度验证,数据表明所建立的推力偏差Kriging模型具有较高的全局精度和局部精度。

(3)依据所建立的Kriging模型开展轨控发动机推力影响因素敏感性、不确定性和可靠性分析。结果表明,为提高固体轨控发动机单阀推力偏差可靠度,在控制系统容差确定后,需着重控制喉栓直径、喉栓位移和喷管喉径等喷管构型相关参数不确定性水平,同时有选择地控制推进剂密度、特征速度和药柱直径等装药相关参数不确定性水平以平衡成本。