固体火箭发动机内弹道多参数辨识及精准预示方法①

2023-08-30王德友李世鹏王宁飞

固体火箭技术 2023年4期

张凌,王德友,李世鹏,王宁飞

(北京理工大学宇航学院,北京 100081)

0 引言

固体火箭发动机内弹道学的基本任务是在发动机各种工作条件下计算燃烧室压强随时间和空间的变化规律。零维内弹道计算方法假定燃烧室内参数均匀一致,与一维及多维内弹道计算方法相比更加简便、直观,是工程上应用较多的求解方法[1-2]。发动机的内弹道特性直接决定着整机性能,进而影响着火箭导弹的飞行特性。因此,进一步提高内弹道预示的精度,对保障飞行器工作可靠性有着重要意义。

工程上通常根据单台或多台发动机的实测数据和燃面几何退移规律,对燃速特性等参数进行辨识,以获得更精确的内弹道性能预示结果。目前,业内学者针对发动机内弹道性能精确预示问题,从理论算法修正、参数辨识方法改进等角度开展了研究。如刘杨等[3]基于对发动机实测数据处理误差的理论分析,提出了修正的燃速系数处理方法,该方法可提高具有较高压强比的发动机内弹道预示精度。李春艳等[4]针对短时间工作固体发动机特点,从理论角度对现有内弹道计算方法进行了适应性修改,所得预示结果与实测数据相比具有较高精度。

在辨识参数选择方面,CAVALLINI等[5-6]通过研究Vega固体运载火箭发动机实际飞行性能影响因素,发现喷管喉部烧蚀率对推力和燃烧室压强的影响较大。BIANCHI等[7]采取数值仿真方法研究喷管喉部烧蚀率和燃速变化对燃烧室压强的影响,发现这两个参数的改变对压强-时间曲线影响十分明显。李晓斌等[8]基于发动机工作过程的内弹道数学模型及实测燃烧室压强时变数据,通过参数辨识方法可对燃速、喉衬烧蚀率等参数进行计算。

在参数辨识方法改进方面,由于最小二乘法、最大似然法等传统辨识方法常存在初始点敏感等问题,因而如遗传算法等具有初值稳健性和全局搜索性的方法在内弹道参数辨识领域逐渐得到深入应用。樊超等[9]将遗传算法用于固体火箭发动机参数辨识,获得了推进剂燃速模型和喉径变化模型的全局最优辨识值,所得内弹道性能预示结果与试验测量值吻合良好。庄建华等[10]对发动机贮存老化内弹道性能的影响因素进行参数建模,基于拉丁超立方设计方法进行了瞬态参数辨识,结合非定常内弹道模型对发动机贮存老化内弹道进行了预示。蒲晓航等[11]基于部分实测压强数据,通过遗传算法逆向反算获得预示参数,再结合正向计算实现了内弹道的预示自修正,对复杂环境剖面下的发动机内弹道性能进行了准确预示。孙瑞阳等[12]建立了基于经典AlexNet卷积神经网络的内弹道参数辨识方法,对长期贮存发动机推进剂装药的燃速特性参数进行了辨识。张小平等[13]建立了高能固体推进剂的配方表征方法,利用遗传神经网络(GA-BP)对推进剂高压燃烧性能及其变化规律进行了预示。

传统发动机的实测数据处理常通过燃烧时间内的平均压强和药柱平均燃速计算获得燃速系数等参数并反算燃面,而实际上平均压强与平均燃速间并不符合燃速模型对应关系[3],因而计算存在一定误差。而目前的研究工作大多采用遗传算法和神经网络等方法对关键内弹道参数进行辨识,并没有根据实测数据对药柱燃面以及内弹道参数进行修正与二次辨识,内弹道参数辨识以及性能预示的精度还可以进一步提高。因此,有必要对关键内弹道参数开展二次辨识,得到更加精确的辨识结果,进而提高发动机内弹道预示精度。

本文提出了一种发动机内弹道多参数辨识及性能精准预示方法,根据发动机实测压强数据,通过遗传算法对燃速系数、压强指数、推进剂密度和喷管喉衬烧蚀速率系数开展初步辨识,基于辨识结果修正燃面-肉厚关系,在此基础上开展二次参数辨识,最终确定关键内弹道参数。根据第二次参数辨识结果和修正后的燃面-肉厚关系,通过正向预示可获得发动机的内弹道性能。以美国C1xb型发动机[14-15]和国内某型长通道发动机[16]为案例进行计算分析,验证了该方法内弹道性能预示的精度和有效性,相关结果可为固体火箭发动机的优化设计提供技术参考。

1 内弹道预示模型

本文以零维内弹道模型[17-18]为基础进行发动机性能正向预示,该模型有如下假设:(1)燃气为理想气体,气体流动为零维定常流动;(2)装药点燃过程瞬时完成;(3)喷管喉衬烧蚀速率与燃烧室压强正相关。在考虑点火药和喷管喉衬烧蚀作用对内弹道计算影响的情况下,结合燃烧室内质量守恒定律、能量守恒定律、燃烧室内体积守恒方程、燃速方程以及气体状态方程,推导出的内弹道微分方程组如下:

(1)

其中,

(2)

(3)

(4)

(5)

2 多参数辨识及精准预示方法

考虑到发动机试验成本问题,基于一次或几次试车数据开展发动机内弹道关键参数的精确辨识研究,对降低固体发动机设计成本和提高设计效率有着重要意义。基于工程中的内弹道参数辨识方法,本文提出一种发动机内弹道多参数辨识及预示方法,可提高内弹道预示精度。

2.1 工程中内弹道参数辨识方法

(6)

(7)

(8)

式中W为装药肉厚;t为燃烧时间;Ab为燃面面积;At为喷管喉部面积;C*为特征速度。

2.2 多参数辨识及精准预示方法流程

上述平均燃速和平均压强并不具有实际对应关系,计算存在一定误差,在内弹道预示精度上仍有较大优化空间。本文提出了一种内弹道多参数辨识及精准预示方法,该方法是对工程办法的改进。以单台发动机的实测压强数据为基础,在发动机稳定工作段选取部分时间段进行计算,基于所建立辨识修正方法获得燃速模型参数和燃面-肉厚数据等内弹道预示所需全部关键参数,进行内弹道性能预示,该方法能提高内弹道预示精度,具体流程如图1所示。

图1 多参数辨识及精准预示方法流程Fig.1 Multi-parameter identification and prediction method process

从发动机实测压强数据出发,基于GA遗传算法对燃速系数a、压强指数n、推进剂密度ρp及喷管喉衬烧蚀速率系数as进行第一次参数辨识。通过参数辨识结果和燃面-压强公式对燃面-肉厚曲线进行反算,进而更新多参数辨识的计算模型,再通过所得燃面数据和遗传算法开展第二次参数辨识。根据二次辨识结果对初次辨识参数进行修正,在第一章介绍的内弹道预示模型的基础上,根据所得参数及燃面数据对发动机内弹道性能开展正向预示。

2.3 基于遗传算法的内弹道多参数辨识

内弹道多参数辨识主要根据发动机工作时间内的实测压强数据进行逆向反算,该工作基于GA遗传算法完成,对燃速系数a、压强指数n、推进剂密度ρp及喷管喉衬烧蚀速率系数as四个参数进行辨识,具体步骤如下:

(1)根据实测数据信息及设计经验,选定时间间隔Δt,作为计算两条曲线拟合程度的最小时间微元;

(2)给定参数初值范围,其中燃速系数a和压强指数n还需满足燃速模型关系,故需施加额外限制条件;

(3)在给定初值范围内,随机给出N组数据(a,n,ρp,as)作为模型初始群体,每组数据为初始群体的个体;

(4)根据零维内弹道理论建立正向预示数学模型,基于任意一组数据可进行一次内弹道性能预示,即N组数据可获得N条压强曲线;

(5)由于发动机稳定工作段数据更具代表性,故在稳定工作段内以Δt为间隔总计选取M个节点,建立内弹道预示模型的适应度函数,其为M个节点处预示压强与实测压强的差值组成的行向量,该行向量的范数作为衡量该组数据适应度高低的判据;

(6)淘汰适应度低的初始个体,保留适应度高的初始个体,在保留个体间进行数据的交换和变异,形成初始群体的子代,再次通过适应度函数对新群体进行选择;

(7)重复上步操作直至结果收敛,将适应度最高的数据代入内弹道预示模型中,即可获得与实测数据吻合度最高的压强曲线。

上述为初次参数辨识的步骤。基于初次参数辨识结果进行燃面反算,根据反算燃面数据更新内弹道预示数学模型,再进行二次参数辨识修正。第二次辨识的参数初值范围可适当缩小,以加快收敛速度并提高效率。

3 案例计算分析

为验证内弹道性能预示方法的准确性和有效性,本文选取C1xb型发动机和一种长通道发动机作为研究案例。

3.1 C1xb型发动机案例

C1xb型发动机的装药组成为79% AP和21% HTPB的复合推进剂,该发动机结构参数和试车数据较为详尽[15],许多关于发动机燃烧稳定性和内流场特性的研究均选取该发动机作为验证案例。该型发动机的具体参数如表1所示,结构如图2所示。

表1 C1xb发动机参数Table 1 Parameters of C1xb SRM

图2 C1xb发动机结构图Fig.2 Schematic of C1xb SRM

3.1.1 第一次参数辨识

(1)取最小时间微元Δt=0.01 s进行曲线拟合度对比计算;

(2)在稳定工作段内,以Δt为时间间隔选取300个点作为曲线拟合度计算时间节点;

(3)计算所有节点上预测压强值与实测压强值的差向量,将该行向量的Euclid范数作为适应度函数。

C1xb发动机实测压强曲线存在初始尖峰,根据工程经验可知其为点火药与装药共同燃烧导致产气量剧增所致[17-18]。点火过程影响因素较为复杂,但其对内弹道曲线整体趋势影响并不显著。辨识计算中取发动机稳定工作部分时间段作为计算区间,避开初始点火过程和压强下降拖尾段,以提高多参数辨识的精度。

在第一次多参数辨识的过程中,设定4项待辨识参数的初始取值范围分别为3.5 mm/(s·MPan)≤a≤5 mm/(s·MPan),0.4≤n≤0.5,1550 kg/m3≤ρp≤1650 kg/m3,0.1 mm/(s·MPa)≤as≤0.2 mm/(s·MPa)。基于遗传算法进行多参数辨识,在经过多次迭代计算后结果收敛,求解过程如图3所示。初次参数辨识结果为:燃速系数a=4.48 mm/(s·MPan),压强指数n=0.487 6,推进剂密度ρp=1556 kg/m3,喷管喉衬烧蚀速率系数as=0.138 7 mm/(s·MPa)。

图3 第一次遗传算法优化求解过程Fig.3 Calculation progress of first multi- parameter identification

由于原始文献未给出发动机点火装置参数,且点火过程对宏观内弹道特性影响较小,故将点火药假定为球形颗粒黑火药,再基于遗传算法和考虑点火过程的内弹道预示模型对点火药质量和颗粒粒径进行辨识。该过程所需其余参数采用初次参数辨识的结果,最终获得点火药质量为2.5 g,粒径为1.5 mm。根据参数辨识结果进行内弹道预示,可获得初步预示的压强-时间曲线,如图4所示。

图4 第一次辨识计算结果与实测数据对比Fig.4 Comparison between first prediction and measured pressure data

3.1.2 燃面反算及第二次参数辨识

基于初次参数辨识结果,根据燃面-压强公式进行燃面反算。为避免点火过程对反算燃面数据产生影响,在计算时不考虑点火药燃烧的影响,可获得如图5所示的反算燃面-肉厚曲线。

图5 反算燃面-肉厚曲线Fig.5 Inverse calculation of burning area-web curve

在初次辨识基础上开展二次辨识,基于反算燃面数据对已有数学模型进行更新。为加速收敛,第二次辨识的参数初值范围相较第一次辨识适当缩小。设定4项待辨识参数的初始取值范围分别为4.2 mm/(s·MPan)≤a≤4.8 mm/(s·MPan),0.45≤n≤0.5,1550 kg/m3≤ρp≤1600 kg/m3,0.12 mm/(s·MPa)≤as≤0.2 mm/(s·MPa)。如图6所示,经过多次迭代计算后结果收敛,第二次参数辨识结果为:燃速系数a=4.648 mm/(s·MPan),压强指数n=0.455 1,推进剂密度ρp=1589 kg/m3,喷管喉衬烧蚀率系数as=0.142 3 mm/(s·MPa)。根据反算燃面数据和第二次参数辨识结果再次进行内弹道预示,可获得图7所示的修正压强-时间曲线。由图7可知,第二次性能预示精度较第一次更高,且预示结果与实测数据高度吻合。

图6 第二次遗传算法优化求解过程Fig.6 Calculation progress of second multi- parameter identification

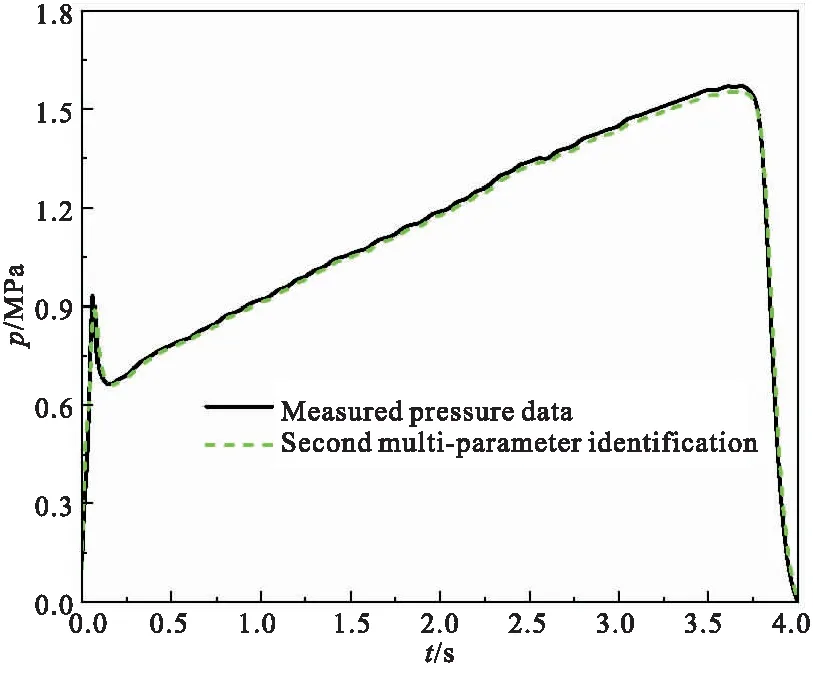
图7 第二次辨识计算结果与实测数据对比Fig.7 Comparison between second prediction and measured pressure data

3.2 某型长通道发动机案例

测试案例二为某型长通道固体发动机,该发动机装药为端面包覆的内外燃管形装药,采用双基推进剂并以黑火药为点火药,其相关参数较为详尽[16],具体结构参数如表2所示,结构图如图8所示。

表2 长通道发动机参数Table 2 Parameters of the long passage SRM

图8 长通道发动机结构图Fig.8 Schematic of the long passage SRM

应用上述介绍的内弹道多参数辨识方法对该长通道发动机进行第一次参数辨识,第一次参数辨识结果为:燃速系数a=3.01 mm/(s·MPan),压强指数n=0.444 1,推进剂密度ρp=1563 kg/m3,喷管喉衬烧蚀率系数as=0.112 2 mm/(s·MPa)。用第一次多参数辨识结果进行燃面反算,根据内弹道预示模型进行性能预示,计算得到如图9所示的燃烧室压强预示曲线和如图10所示反算燃面曲线。由于燃面数据计算采用式(8)所示的工程方法,故上升段和下降段与实际燃面变化的物理过程存在一定差异。

图9 长通道发动机第一次辨识预示曲线Fig.9 First prediction of the long passage SRM

图10 长通道发动机反算燃面-肉厚曲线Fig.10 Inverse calculation of burning area-web curve of the long passage SRM

根据反算燃面数据更新模型后,进行第二次多参数辨识,得到最终参数辨识结果为:燃速系数a=3.09 mm/(s·MPan),压强指数n=0.440 5,推进剂密度ρp=1564 kg/m3,喷管喉衬烧蚀率系数as=0.113 1 mm/(s·MPa)。由于辨识计算过程的主要依据为发动机稳定工作段压强数据,故所得辨识参数结果具有较好的合理性。把反算的燃面数据以及修正后的参数代入内弹道正向预示模型进行计算,可获得如图11所示的燃烧室压强曲线。由图11可知,第二次性能预示精度较第一次更高,且预示结果与实测数据高度吻合。