机器人针刺成型异形预制体的路径规划①
2023-08-30邵建娜张雅秀曾欣怡李嘉禄
邵建娜,张雅秀,曾欣怡,蒋 云*,李嘉禄
(1.江南大学 纺织科学与工程学院,无锡 214122;2.天津工业大学,天津 300387)
0 引言
纤维预制体是采用定型剂或纺织方法将增强纤维预成型为特定形状的纤维复合材料增强体。针刺作为一种工艺简单、低成本的织物增强成型制备技术而被航空航天领域广泛应用,使用该技术制备的纤维复合材料比强度、比刚度高,抗疲劳性能良好[1-2]。三维针刺成型技术的原理是使用带倒钩的刺针反复刺入纤维网,当刺针的倒钩进入纤维网时,由于纤维之间摩擦力的作用,使得原本有序的纤维交叉缠绕在一起,经过大量反复的针刺,最终得到具有良好力学特性的针刺复合材料预制体。
三维针刺成型技术适用于制备平板预制体、圆环预制体、圆柱和圆锥预制体,以及具有复杂曲面形状的预制体。在过去的几十年时间里,国内外的研究单位及科研工作者对三维针刺预制体的成型装备开展了广泛的研究[3]。OLRY[4]发明了一种可以制备高厚三维针刺预制体的针刺机,该设备在厚度方向具有较大的工作范围,可以用于制备不同厚度的平板预制体。为了进一步扩展针刺机的适用性,RENAUD等[5]公开了一种环形纤维预成型构件的制造方法,该方法可以实现环向纤维的自动铺放和针刺,自动化程度更高。航空航天用构件通常具有较为复杂的曲面形状。OLRY和RENAUD发明的平板和圆环预制体针刺机不能很好的满足近净成型的要求,限制了三维针刺预制体及其复合材料的开发和应用[3]。OLRY[6]在之前的基础上发明了用于异形纤维预制体的针刺设备,由四自由度机械臂拖动针刺头完成针刺,针刺头角度可在0~90°范围内进行调整,特别适合椭球、圆锥等特定类型的非封闭壳体制品的针刺工作[7]。后续,FRANCOIS等[8]设计了一款数控复合材料纤维增强针刺设备,设备采用龙门架式结构并配有数控系统,工作范围更大,自动化程度更高,可进行平面、曲面的针刺任务,缺点是针刺角度不可调节[7]。由于技术封锁的原因,国外在机器人复合材料三维针刺成型领域应用研究的资料寥寥无几。国内有天津工业大学的陈小明[3]借助CATIA软件开发了机器人针刺路径规划算法,缺点是该算法依赖其他第三方软件。童宁[9]对PCA算法进行改进得到一种具有广泛适应性的喷枪姿态获取方法。周仁义[10]采用基于Zernike矩的亚像素轮廓提取方法,通过NURBS曲线拟合的方法得到机器人运动路径。
在机器人快速发展的今天[11-15],本文在此背景下对异形预制体机器人针刺成型路径规划进行研究,解决异形变截面预制体变密度针刺,棱边和大面不同植针数量末端执行器无缝衔接针刺,实现轮廓形状可变,纤维体积含量的精确控制,推动三维针刺装备快速发展,助力中国航天事业。
1 异形预制体机器人针刺路径生成方法
由于自由曲面的灵活性使得异型预制体针刺路径生成较为困难,主流的等参数法具有较大的局限性。为此,本团队提出了基于切片法的异型预制体机器人针刺路径生成方法[7],将预制体模型保存为STL格式并提取其中的三角面几何信息,采用多个平行切平面与STL模型文件三角面求交得到异型预制体针刺路径型值点集合,如图1所示。然后利用交点冗余信息对针刺路径点集进行优化排序。最后,使用3次NURBS方法对针刺路径型值点进行拟合[7],从而得到机器人针刺路径以及路径表达式。图中,T1、T2、…、T9为STL文件包含的三角面;i-2、i-1、…、i+2为多个切平面;a、b、…、e为i+2层切平面与三角面的交点,后文统称为针刺路径型值点。
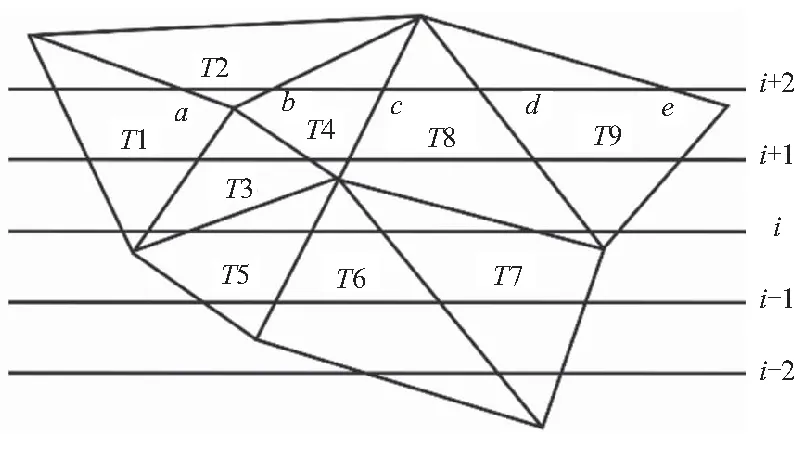
图1 异形预制体机器人针刺路径生成示意图Fig.1 Schematic diagram of needling path generation for special-shaped preform robot
1.1 STL模型文件特点
STL文件是计算机图形应用系统中使用三角面集合去描述物体的一种文件格式,该格式文件可以根据不同的精度要求对模型表进行网格划分,将模型表面离散为许多三角面的集合,每个三角面记录着三角面的三个顶点坐标和外法向矢量[9]。不同于其他模型文件(STEP、IGES等),该格式文件只限于几何信息数据在3D物体的表面,而没有描述三角面之间的拓扑关系。文本格式的STL文件数据结构如下:
solid film name.stl//模型文件名称
facet normalnxnynz//法向量的3个分量值
outer loop
vertexx1y1z1//第一个顶点坐标
vertexx2y2z2//第二个顶点坐标
vertexx3y3z3//第三个顶点坐标
endloop
endfacet //结束第一个三角面定义
……//其余三角面定义
end solid //文件结束声明
1.2 三角面与切平面交点计算
三角面与切平面交点计算的基本算法是当前切平面与一个三角面相交,以Z轴为切片方向进行说明。经过分析,切平面与三角形面片的相交情况存在以下4种(见图2):
(1)X-Y切平面与三角面的一个顶点相交;
(2)X-Y切平面与三角形面片的两个顶点相交;
(3)X-Y切平面与三角形面片的一条边和一个顶点相交;
(4)X-Y切平面与三角形面片的两条边相交。
设三角面的三个顶点坐标分别为v1(x1,y1,z1)、v2(x2,y2,z2)、v3(x3,y3,z3),th为切片间距,z0为Z轴方向切片的起始高度。假设当前位于第i个切片层,在Z轴方向高度为
zi=i·th+z0
(1)
当X-Y切平面与小三角形面片的一个顶点相交时,说明该顶点就是在当前切平面上的一个针刺路径点,如图2(a)所示,二者相交于v1点,则针刺路径型值位置信息为
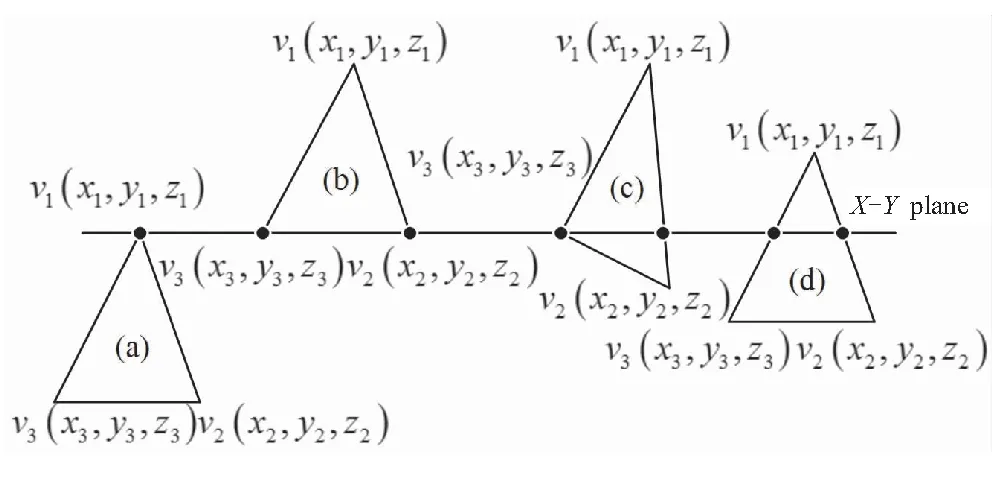
图2 三角面相交的情况分析Fig.2 Analysis of triangular patch intersection
(2)
当X-Y切平面与小三角形面片的两个顶点相交时,说明三角面的一条边与切平面重合,此时该条边的两个顶点就是在当前切平面的两个针刺路径点,如图2(b)所示,二者相交于v2和v3点,则针刺路径型值点位置信息分别为

(3)
当X-Y切平面与小三角形面片的一条边和一个顶点相交时,此时产生两个针刺路径点。其中一个为三角形的一个顶点,二者相交于v3点;另一个位于三角形边v1v2上,可以使用相似三角形原理求解三角形边v1v2上的针刺路径点位置信息,如图2(c)所示,则针刺路径点位置信息分别为
(4)
和
(5)
当X-Y切平面与三角形面片的两个边相交时,说明该切片层与三角形面片相交产生两个针刺路径点,两个针刺路径点分别位于三角形面片的两条边上[9],如图2(d)所示,此时两个针刺路径点分别为
(6)
和
(7)
1.3 基于交点冗余信息的针刺路径型值点排序
由于STL模型丢失了原物理模型之间的拓扑关系,三角形的记录顺序杂乱无章,为了使交点坐标有序排列,需要对其重建三角形间的拓扑关系。由于STL模型三角形之间存在共边原则,因此在切片过程中存在着冗余的交点信息,本文基于此信息利用逐点识别与剔除的思想重建拓扑关系,进而对针刺路径型值点进行排序[10]。
根据STL文件共边规则,三角形面片共用一条边,T1、T2三角形与切平面的交点记录形式[ab]、[cd][10],分别为面片T1和面片T2的针刺路径型值点,坐标值b=c,在顺时针记录有序点坐标时可将点坐标视为点坐标的冗余交点。因此,利用三角形与切平面的交点坐标可快速查到其冗余交点坐标,得到三角形的邻接三角形,从而得到针刺路径点型值点顺序为a、b、d或a、c、d,冗余交点如图3所示。

图3 交点冗余信息示意图Fig.3 Schematic diagram of intersection redundancy information
1.4 基于NURBS曲线拟合的针刺路径生成
经过1.2和1.3节的运算,将排序后的针刺路径型值点拟合就形成了针刺路径,针刺路径型值点是后续规划针刺点位置和姿态的基础数据。由于NURBS方法灵活性和连续性好的优点目前已在CAD/CAM领域获得广泛应用,且这种方法已经成为产品数据交换的国际标准。因此,本文采用NURBS方法进行针刺路径点拟合。一条k次的NURBS曲线可以由以下有理分式表示[7]:
(7)
其中,di(i=0,1,…,n)为控制顶点;ωi(i=0,1,…,n)为权因子,与控制顶点di一一对应;Ni,k(u)是由节点矢量U=[u0,u1,…,un+k+1]通过德布尔-考克斯递推公式决定的k次B样条基函数,其递推公式为[11]
(8)
设1.3节获取的针刺路径型值点序列为pi(i=0,1,…,n),由于3次NURBS曲线完全满足实际应用中的要求,所以本文应用3次NURBS曲线进行针刺路径型值点拟合,拟合流程图如图4所示[7]。
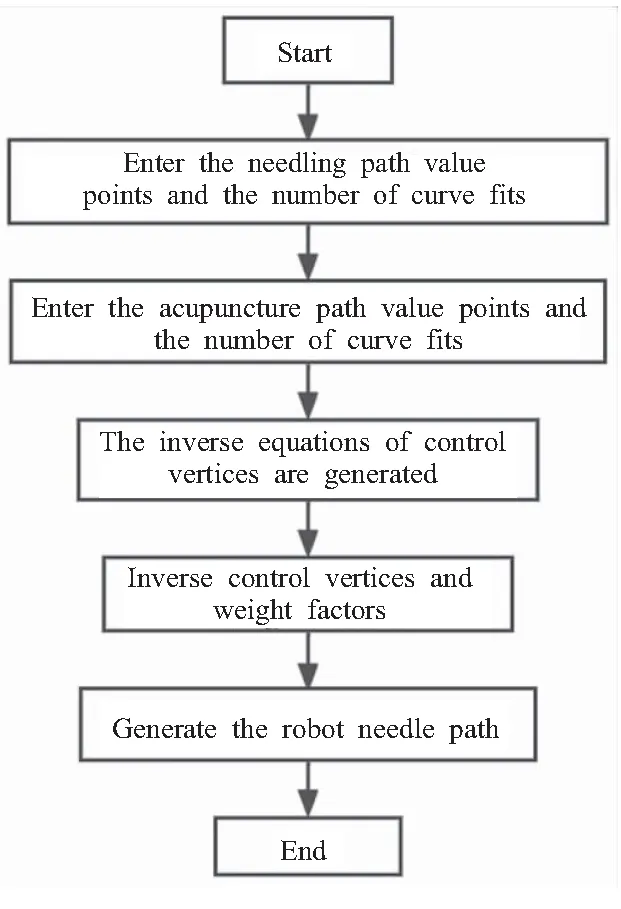
图4 针刺路径型值点NURBS曲线拟合流程图Fig.4 Flow chart of NURBS curve fitting for needling path type value points
(1)型值点参数化
型值点参数化实际上是为每一个型值点pi赋予参数值ui,确定节点矢量U。积累弦长参数化方法是目前公认的最佳参数化法,该方法可以如实地表现出型值点的分布情况,更符合切片法得到的数据点特点,则使用积累弦长参数化方法得到的节点矢量U[12]:
(9)
(2)控制顶点反算
将控制顶点di与权因子ωi重新组合,定义带权控制顶点Di[ωidi,ωi](i=0,1,…,n),转换为齐次坐标形式,它们之间的关系为
(10)
对于C2连续的3次NURBS闭曲线,式(10)中包含n+1个方程,因为首末型值点重合p0=pn,不计重复,方程数减少1个,剩余n个。又首末3个控制顶点依次相重Dn=D0,Dn+1=D1,Dn+2=D2,未知控制顶点数少了3个,剩余n个。因此,就可从n个方程构成的线性方程组求解出个n个未知不重复带权控制顶点[13]。将式(10)改写为矩阵形式:
(11)
其中,
(12)
对于3次NURBS开曲线,式(10)的n+1个方程不足以解决其中包含的n+3个未知控制顶点,还必须增加两个通常由边界条件给定的附加方程[14]。此时求解3次B样条插值曲线未知控制顶点的线性方程组可写成如下矩阵形式:
(13)
其中,系数矩阵中首行非零元素a1、b1、c1与右端列阵中矢量e1表示了首端点边界条件;系数矩阵中末行非零元素an+1、bn+1、cn+1与右端列阵中矢量en+1表示了末端点边界条件[15]。其余各行元素ai、bi、ci(i=1,2,3,…,n)与C2连续闭曲线的情况相同。
边界条件通常采用端点切矢条件,切矢条件相当于力学中的梁的端部固支的情况,该条件具有固定的切线方向。采用端点切矢条件时,首、末端满足下列附加方程[16]:
(14)
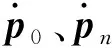
(15)
2 针刺点位置和姿态信息确定
在获得针刺路径的表达式后,根据针刺工艺对针刺路径进行等步长插补,进而得到一系列针刺点位置和姿态信息,将生成的一系列针刺点位姿进行逆运动学求解,运动控制器对各个电机进行脉冲分配,驱动机器人TCP点沿着针刺轨迹移动到针刺点完成针刺。
2.1 针刺点位置信息确定
由于插补节点参数集合{u1,u2,…,un}与插补时间集合{t1,t2,tn}相互对应,以插补时间t为自变量,节点参数u为因变量建立函数。将参数u对时间t的函数在ti时刻进行泰勒展开,则有
(16)
记T=ti+1-ti,则在t=ti+1时刻可得
(17)
略去式(17)中高阶项,只保留到二阶项,记u(ti)=ui,u(ti+1)=ui+1,即可得插补参数u的递推公式为
(18)
由式(18)可知,插补参数的计算问题转换为了节点参数u对时间t的求导问题。若机器人末端TCP点始终沿着曲线移动,则理想插补速度Varc(ui)为
(19)
用给定进给速度V(ui)近似代替理想进给速度Vace(u)并将式(19)变形得
(20)
对式(20)求导得
(21)
因此,基于泰勒展开法的插补参数计算公式为
(22)
为了统一描述插补参数计算误差的大小,引入速度波动率δ作为评价标准:
(23)
速度波动率δ值越小,插补参数越接近理想值。
二阶泰勒展开法计算插补参数均要进行复杂的求导运算,不利于算法的实时性,同时算法截断误差较大。为此本文提出了基于四阶Runge-Kutta的插补参数预估校正法,该方法首先运用Runge-Kutta法对插补参数进行预估计算,之后使用校正公式对得到的插补参数进行修正,使速度波动率保持在限定的范围内,提高插补参数的计算效率和计算精度,确保针刺点间距一致。
将四阶Runge-Kutta法运用到NURBS曲线插补中用以计算插补参数。插补参数计算过程中,时间t为自变量,参数u为因变量,T为时间间隔(插补周期),T=ti+1-ti,已知在ti时刻对应插补参数为ui,给定进给速度V(ui),目标是求解处时刻ti+1的插补参数ui+1,因此建立非线性微分方程:
(24)
由二阶泰勒展开法可得
(25)
由四阶Runge-Kutta法可得
(26)
其中,
(27)
四阶Runge-Kutta法与二阶泰勒展开法相比,只需要进行一阶导数的运算,避免了二阶导数的运算,同时提高了计算精度,但是相较于理想的插补参数还是有一定的偏差,主要原因是用给定的插补进给速度V(ui)替代理想进给速度Varc(ui)。对此以速度波动率作为优化目标设计校正算法对四阶Runge-Kutta法计算出的插补参数初值进行修正,提高插补参数的计算精度,保证各个周期插补步长一致。
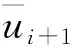
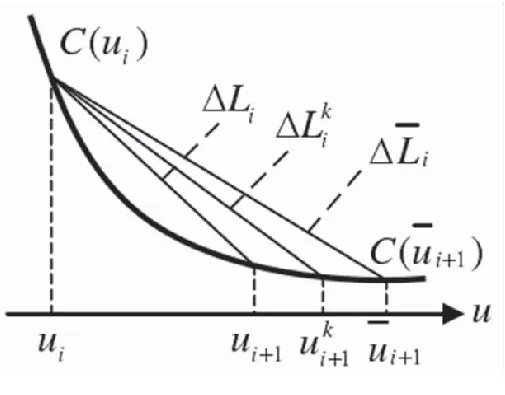
图5 基于速度波动率的插补参数校正示意图Fig.5 Schematic diagram of interpolation parameter correction based on velocity fluctuation rate
本文设计的修正策略如下:
(28)
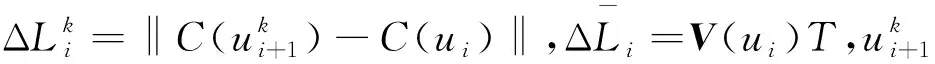
基于四阶Runge-Kutta法的预估校正法插补参数计算流程如图6所示。

图6 基于四阶Runge-Kutta的预估校正 插补参数计算流程图Fig.6 Calculation flow chart of predictive correction interpolation parameters based on fourth order Runge Kutta
具体计算步骤如下:
Step1:初始化i=0,ui=0;

Step3:采用本文设计的四阶Runge-Kutta法计算式(26),计算初始插补参数ui+1;
Step4:计算出插补参数ui+1处的插补点坐标C(ui+1),得到当前插补参数ui+1插补时的实际进给步长ΔLi;
Step5:根据式(23)计算速度波动率,若δi=δmax,则跳转到Step6;否则,采用式(28)对插补参数进行校正,返回Step4;
Step6:判断是否满足ui+1≥1,如果满足,表明此时已经到达NURBS曲线的终点,令ui+1=1,结束插补;否则返回Step2。
将基于四阶Runge-Kutta的预估校正得到的插补参数u代入式(7)中即可得到针刺点位置坐标信息。2.2 针刺点姿态信息确定
假设基于四阶Runge-Kutta的预估校正法求得的某个针刺点对应的节点参数为u,从而确定节点参数u位于的节点区间,即u∈[u3+i,u4+i]。采用二分搜索法在节点矢量U的子区间{u3,u4,…,u2+n,u3+n}中搜索节点区间的下标i,即可确定针刺点在型值点pi与pi+1之间[7]。
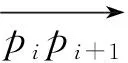
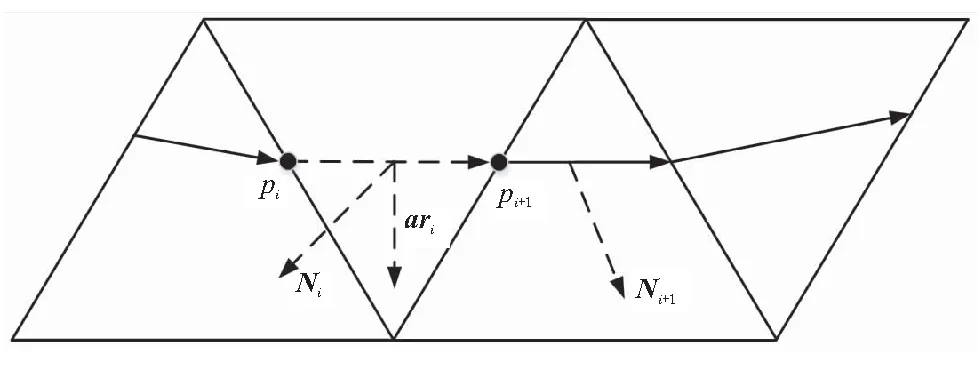
图7 姿态笛卡尔坐标系建立Fig.7 Establishment of attitude Cartesian coordinate system
则所有针刺点与其相邻两个型值点连线组成的边的集合为
(29)
针刺点相邻两个型值点所在三角面的法向量集合可表示为[7]
(30)
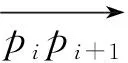
(31)
由上述可知,机器人第i个针刺点的姿态信息可以表示为[9]
(32)
由于机器人RPY角姿态描述方式较为常用,将姿态矩阵转换为RPY方式。机器人姿态的RPY描述方法如图8所示,首先绕a轴旋转α角,再绕o轴旋转β角,最后绕n轴旋转γ角,α、β、γ分别为其滚动角、俯仰角和偏航角[7]。

图8 机器人姿态RPY描述方式Fig.8 RPY description mode of robot attitude
机器人RPY姿态转换矩阵表示为
Rot(a,α)Rot(o,β)Rot(n,γ)=
(33)
式中 cα、cβ、cγ分别为代表cosα、cosβ、cosγ; sα,sβ,sγ分别代表sinα、sinβ、sinγ。
式(33)中包含α、β、γ三个耦合角,为了求解α、β、γ的具体值,需要对矩阵进行解耦。假设机器人期望姿态为
(34)
将式(34)左乘Rot(a,α)-1可得
(35)
将式(35)展开:
(36)
令式(36)中(2,1)元素对应相等:
nycα-nxsα=0
(37)
解得
α=arctan 2(ny,nx)
(38)
令式(36)中(1,1)和(3,1)项分别对应相等:
(39)
解得
β=arctan2[-nz,(nxcα+nysα)]
(40)
令式(36)中(2,2)和(2,3)项分别对应相等得
γ=arctan 2[(-aycα+axsα),(oycα-oxsα)]
(41)
3 仿真验证
为了验证上述算法的有效性和稳定性,选取某导弹天线罩预制体三维模型进行仿真实验,异型预制体三维模型如图9所示。

图9 某导弹天线罩预制体三维模型图Fig.9 3D model drawing of a missile radome preform
选取X轴为切片方向,切片间距设置为100 mm,得到每一个切片层的交点坐标数据并基于交点冗余信息的针刺路径型值点排序,仿真结果如图10所示。

图10 针刺路径点Fig.10 Needling route point
由于每个切片层切片形状基本一致,为了简化仿真流程,选取单个切片层验证针刺路径点NURBS曲线插补算法,仿真结果如图11所示。图11中,各个坐标原点为针刺点位置,绿色为针刺点法向矢量,红色为针刺点切向矢量,蓝色为针刺点轴向矢量。三个矢量构成了针刺点的姿态信息。
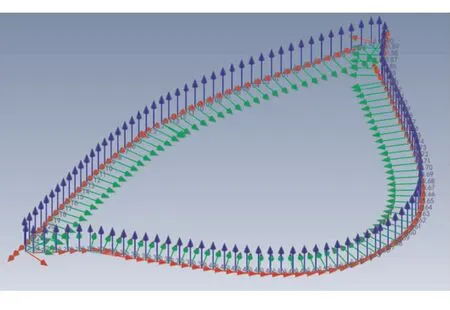
图11 机器人针刺点位置和姿态生成Fig.11 Generation of robot needling position and attitude
速度波动率描述了插补误差的大小,进而反映了针刺的均匀性。在此基础上,运用二阶泰勒展开法和基于四阶Runge-Kutta的预估校正法对机器人针刺路径进行插值仿真。仿真插补参数如下:给定进给速度V=100 mm/s,插补周期为T=0.04 s,即插补步长为4 mm,最大速度波动率δmax=10-2%,以速度波动率为判定标准比较二阶泰勒展开法以及基于四阶Runge-Kutta的预估校正两种插补参数计算方法。
采用二阶泰勒展开法进行仿真,结果如图12所示。仿真结果表明,速度波动率最大为6.4%,在u=0.2、u=0.6处出现突变,此时针刺点刚好位于针刺轨迹最大曲率处,原因在于插补节点参数u计算时是用给定的弦长进给速度代替理想的切线方向进给速度,这时两者差距较大,因此出现剧烈变化,说明此时针刺点间距与理想值偏差较大。该算法由于没有考虑对速度波动率的限制,所以导致速度波动率远远超过最大允许速度波动率[17]。
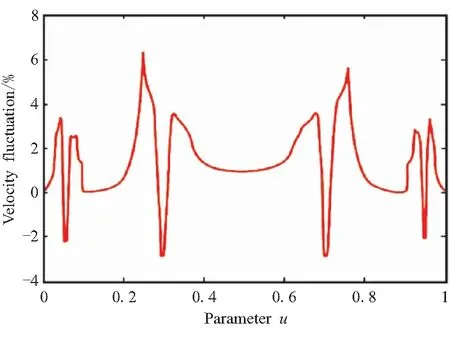
图12 二阶泰勒展开法的速度波动率Fig.12 Velocity fluctuation rate of second order taylor expansion method
如图13所示,采用基于四阶Runge-Kutta的预估校正法使得最大速度波动率限制在给定10-2%内,计算精度明显提高,原因在于四阶Runge-Kutta算法精度比二阶泰勒展开法高,同时对计算得到的插补参数进行校正,保证速度波动率限制在预设的范围内。

图13 基于四阶Runge-Kutta的预估校正法速度波动率Fig.13 Velocity volatility of predictor corrector based on fourth order Runge Kutta
综合以上分析,基于四阶Runge-Kutta的预估校正法在速度波动率方面明显优于二阶泰勒展开法,插补参数的计算更加准确,保证了针刺点的均匀性,且不需要计算高阶导数,计算速度也有所提升,充分体现了算法的有效性[17]。
仿真结果表明,该算法灵活性好,稳定性强。可以设置切片间距和切片方向以满足不同针刺工艺要求的异型预制体针刺点位置和姿态生成,对于实际生产具有一定的意义。
机器人实物验证验证在本课题搭建的机器人针刺成形单元中进行,如图14所示。针刺机器人采用广州数控(RB50),针刺工具为自主研制的气动针刺头,如图15所示。其余部件还包括空气压缩机、电磁阀、工件工装等。

图14 机器人针刺单元实验平台Fig.14 Robot needling unit experiment platform
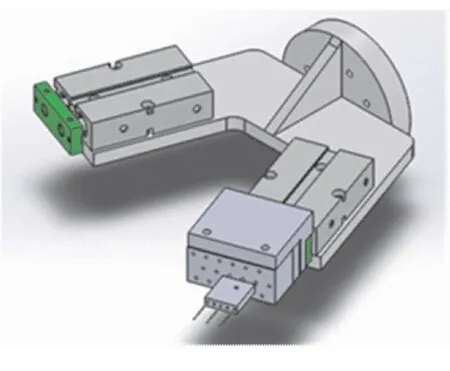
图15 针刺工具三维模型Fig.15 3D model of needling tool
异形预制体针刺加工验证如图15所示,针刺点位姿与规划值基本一致,图16为针刺效果的局部放大图,经过测量,针刺间距和针刺深度满足针刺要求。

图16 实际加工验证Fig.16 Actual processing verification

图17 针刺后的异形预制体Fig.17 Special-shaped preform after needling
4 结论
(1)本文对异型预制体机器人针刺成型路径规划进行研究,提出了一种基于切片法的机器人针刺路径规划方法。将多个平行切平面与预制体STL模型文件中包含的三角面进行求交运算,从而实现了异形预制体CAD模型到机器人针刺路径的自动生成。
(2)采用基于四阶Runge-Kutta的预估校正法,用于NURBS曲线等步长插补参数的计算,得到针刺点位置;选取针刺点相邻路径型值点的法向量和位置坐标,结合机器人RPY姿态描述方式,得到了针刺点的姿态。
(3)仿真结果表明,该路径规划算法灵活有效,为异型预制体机器人针刺成型路径规划提供了一种简便有效的方法。
后续,结合此路径规划方法进一步提高效率还可采用电动凸轮驱动提高针刺频率和针刺力,可制作更厚、密度更高的预制体。
