直面复杂问题挑战的数学主题创新活动——以六年级《圆锥形纸杯面积有多大》主题拓展教学为例

卢 琴 蒋守成

数学主题创新活动，是指引导儿童在直面复杂问题挑战过程中形成新体验、获得新见解的跨学科数学学习活动。主题就是要解决的问题，是学生能够主动参与的、有真实情境的、具有挑战性的复杂问题。创新活动就是解决问题的过程，是指围绕复杂问题的解决，学生综合运用已有的生活经验和数学知识以及其他相关学科的知识，通过独立思考、合作探究等数学学习活动，创造性地解决问题，并在此过程中获得新经验、产生新思考、形成新见解。数学主题创新活动的实施主要分为四步：确立项目主题—设计项目方案—进行项目探究—展示活动成果（如图1）。

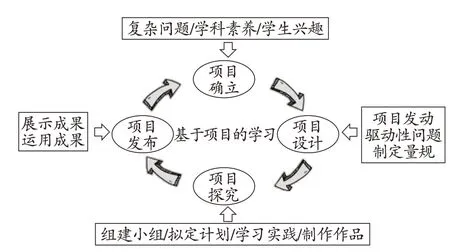
（图1）

下面，笔者以教学苏教版六下“圆柱与圆锥”单元时自主设计的《圆锥形纸杯面积有多大》一课为例，谈谈如何设计直面复杂问题挑战的数学主题创新活动。

一、聚焦生活，确立项目主题

数学主题创新活动的“主题”是种子，来源于学生的真实生活和真实问题，根植于学生的认知和生活经验。主题的确立基本上决定了主题创新活动的深度和广度。

师：同学们，老师这儿有一个喝水的纸杯，这个纸杯和我们平时见过的纸杯有什么不一样？

生：这是一个圆锥形的纸杯，我们平时见到的大多是圆柱形的纸杯。

师：你有没有在哪里见过或使用过这种圆锥形纸杯？

生1：我在商场购物时，看到饮水机旁边放着这种圆锥形纸杯。

生2：我在高速公路上的服务区用过。

师：确实，在大商场、服务区、飞机场、火车站等人流密集地可能会用到这种圆锥形纸杯。那你知道为什么要在这些地方使用圆锥形纸杯吗？大家不妨大胆猜一猜。

生1：圆锥形纸杯更容易拿在手上。

生2：更省材料。

师：我们通过一段视频来了解一下。

播放视频《为什么使用圆锥形纸杯》。

师：原因之一确实是“省纸”，那这个圆锥形纸杯的面积有多大呢？到底省不省纸呢？这就是我们今天的研究主题。

上述教学从生活中的纸杯入手，引导学生思考圆锥形纸杯存在的价值，启发学生联想“圆锥形纸杯面积有多大”这一研究主题，这既是学生源于生活经验自然生发的研究内容，也是单元知识内容的补充，有助于学生完善有关立体图形的认知结构。

二、问题驱动，共生项目设计

在数学主题创新活动中，立足一个或多个问题，以问题解决为驱动力，能有效激活学生主动参与的意识和行为，充分调动学生已有的学习经验进行方案设计与实践探究，使问题真正成为其研究和探索的出发点和归宿。

师：确定研究主题后，我们先讨论设计出可行的研究方案。你打算怎样研究圆锥形纸杯的面积？

生：可以把这个纸杯剪开。

师：剪开后是什么平面图形？

生：剪开后是扇形，扇形的弧就是圆锥的底面周长，扇形的半径是圆锥的这条斜边。

师：扇形的半径是圆锥顶点到底面圆边任意一点的距离，这是圆锥的母线，可以用字母l表示。要求纸杯的面积，也就是求这个扇形的面积。但我们没学过扇形面积的计算方法，怎么办？

生1：我觉得这个扇形好像是整个大圆面积的三分之一。

师：可以用三个扇形拼成一个大圆。

生1：三个扇形拼成圆还有一些剩余，看来这个扇形面积没有正好是圆面积的三分之一。

生2：可以将扇形平均分成若干个小扇形，拼成已经学过的长方形、三角形，然后再推导。

师：从圆面积的推导联想到扇形面积的推导，是否可行？我们可以来尝试进行实践探究。

研究方案是在生生、师生共同交流的过程中逐步明晰并完善的。在上述教学中，学生首先调取圆柱侧面积的研究经验，将圆锥的侧面展开化曲为直进行研究；然后调取圆面积的推导经验，将扇形平均分成若干份，并剪拼转化成学过的图形进行推导。

三、项目探究，共享优势资源

数学主题创新活动能为学生提供广阔的合作探究空间和必要的“脚手架”，并在问题解决的关键处给予点拨和引领，促进学生在研究中积累经验、提升能力。

出示活动要求：（1）试转化。你想把扇形转化成哪种图形？（2）找联系。转化后的图形与圆锥有怎样的联系？（3）推公式。根据已学图形的面积计算公式，推导出圆锥侧面积的计算公式。

生1：我们组将扇形对折，平均分成四个小扇形，然后拼成近似的平行四边形。平行四边形的底是圆锥底面周长的一半（即πr），平行四边形的高是圆锥的母线（l）。因为平行四边形的面积=底×高，所以扇形的面积是圆锥底面周长的一半×母线=πrl。

生2：我们组也是将扇形对折，平均分成四份，但拼成的是近似的三角形。三角形的底是（即πr），三角形的高是2l。因为三角形的面积=底×高÷2，所以扇形的面积=。

生3：我们组将扇形对折，平均分成8 个小扇形，并拼成近似的梯形。梯形的上底是，梯形的下底是，高是2l。因为梯形的面积=（上底+下底）×高÷2，所以扇形的面积=2l÷2=πrl。

生4：我们组把扇形平均剪成4 个小扇形，再补出4 个小扇形，这样就想象成一个近似的平行四边形。平行四边形的底就是圆锥的底面周长，高是母线，所以扇形的面积＝底面周长×母线÷2=2πr×l÷2=πrl。

师：这四种推导过程有什么相同点？

生：都是将扇形转化成已经学过的图形，再根据它们之间的联系推导出扇形的面积。

师：所以，转化这种数学思想方法非常重要。不管是哪种转化，最后都能得出圆锥的侧面积=πrl。

学生合作探究后呈现的作品让人欣喜，既有转化为近似平行四边形的推导过程，也有转化为三角形和梯形的推导过程，甚至有补上相同数量小扇形的想象推导过程。学生思维的火花在分享中碰撞，转化思想的渗透在比较中得到强化，创新意识的培养在课堂中蓬勃生长。

四、项目发布，推广实际应用

主题创新活动有助于学生形成一系列的数学学习策略：疑难问题不放过，刨根究底找原因；举一反三找规律，触类旁通明原理；小组合作常总结，融会贯通学数学；等等。

师：现在，你能计算出圆锥形纸杯的面积了吗？

生：还需要测量。

师：直径7厘米，母线9.5厘米。

生：3.14×3.5×9.5≈104.4（平方厘米）≈1 平方分米，大约手掌大小就能制作一个圆锥形纸杯，视频中说圆锥形纸杯更省纸，我们用数据证明了确实如此。

师：生活中还有哪些物体是圆锥形的？

生1：生日帽。

生2：冰淇淋甜筒。

师（出示图2）：你能计算出一个生日帽和一个冰淇淋甜筒的面积各是多少吗？

（图2）

…………

生：计算冰淇淋甜筒的面积时要注意用侧面积加上底面积。

师：所以，圆锥的表面积=πrl＋πr2。

师：回顾今天的学习过程，我们发现生活中有圆锥形纸杯，确定了研究主题，然后讨论设计出了可行的研究方案，接着进行了实践探究，得出了研究结论，最后将结论在生活中进行了推广应用，这样的研究过程你学会了吗？你在这个过程中有什么体会？

…………

师：但是，圆在生活中，圆锥形纸杯还是比较少见的，常见的是这种圆台形纸杯。联想一下，你还可以确定什么研究主题？

生：圆台形纸杯的面积有多大？

师：如果是这个主题，你打算怎样来研究？今天这节课能给你带来启发吗？

生1：也要把这个纸杯剪开，应该是一个圆形和一个扇环。

生2：也可以通过转化成已经认识的图形来推导出侧面积的计算方法。

生3：还可以将这个扇环延长，就能得到一个扇形，用大扇形的面积减掉小扇形的面积就是扇环的面积。

师：大家举一反三的能力真强！其实，与之相关的研究主题还有很多，如怎样制作圆锥形纸杯或圆台形纸杯，圆台形纸杯的容积有多大，等等。课后，大家可以接着去发现、去探究。

将数学知识和实际生活联系起来，既使学生完善了对圆锥表面积的认知结构，又让他们深刻体会到数学在实际生活中的应用价值。将圆锥形纸杯的面积研究推广到圆台形纸杯的面积研究，既是学生研究经验的再积累，也是学生对主题创新活动过程的再强化，更在学生心田埋下了继续探究的种子。

总之，数学主题创新活动是基于儿童需求开展的探究活动，强调打破学科之间、学校与社会生活之间的壁垒，开发学科育人资源，它承载着儿童创新意识的萌芽、创新思维的开发和创新能力的培养等功能，连接着儿童当下的学习与未来的发展。