Group-Based Successive Interference Cancellation for Multi-Antenna NOMA System with Error Propagation

Cheng Hu ,Hong Wang ,Changxiang Li ,Rongfang Song,*

1 School of Network and Communication,Nanjing Vocational College of Information Technology,Nanjing 210023,China

2 School of Communication and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

3 National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China

Abstract: Non-orthogonal multiple access(NOMA)is viewed as a key technique to improve the spectrum efficiency and solve the issue of massive connectivity.However,for power domain NOMA,the required overall transmit power should be increased rapidly with the increasing number of users in order to ensure that the signal-to-interference-plus-noise ratio reaches a predefined threshold.In addition,since the successive interference cancellation (SIC) is adopted,the error propagation would become more serious as the order of SIC increases.Aiming at minimizing the total transmit power and satisfying each user’s service requirement,this paper proposes a novel framework with group-based SIC for the deep integration between power domain NOMA and multi-antenna technology.Based on the proposed framework,a joint optimization of power control and equalizer design is investigated to minimize transmit power consumption for uplink multi-antenna NOMA system with error propagations.Based on the relationship between the equalizer and the transmit power coefficients,the original problem is transformed to a transmit power optimization problem,which is further addressed by a parallel iteration algorithm.It is shown by simulations that,in terms of the total power consumption,the proposed scheme outperforms the conventional OMA and the existing cluster-based NOMA schemes.

Keywords: multi-antenna NOMA;group-based successive interference cancellation;error propagation;power control

I.INTRODUCTION

With rapid growth of the number of terminal devices,it is a requirement to support massive connectivity in B5G/6G wireless communication system.It is well known that much more concurrent transmissions and an improved user fairness [1,2] can be achieved by using non-orthogonal multiple access (NOMA),which is more spectrum-and energy-efficient than the orthogonal multiple access (OMA).NOMA mainly includes two categories: power-domain and codedomain NOMA.In this paper we focus on the powerdomain NOMA,in which multiple user messages are superposed on the same resource blocks,which are decoded with a predefined order with the aid of successive interference cancellation (SIC) technique [3].According to this basic principle,there exists a couple of issues in the power domain NOMA system.On one hand,for the user detected firstly,the user signals detected later will be treated as the interference.In order to satisfy the data rate requirements of all users,the required transmit power is increased rapidly as the number of concurrent links increases.On the other hand,for the user detected later,it should decode and subtract the messages of the former users.In practice,the error propagation caused by imperfect SIC is inevitable and becomes more serious as the order of SIC increases[4–6].

Multiple-input-multiple-output (MIMO) is a key technology to improve spectral efficiency or reliability in the modern wireless communications.It is a cost-effective way to meet the requirement of huge throughput and massive connections by integrating multi-antenna technique into NOMA system.Since the channel matrices cannot be sorted like the scalars of single-input-single-output (SISO) NOMA system,it is hard to predetermine the order of SIC in multiantenna NOMA system.As a result,the transmission policy design in multi-antenna NOMA system is more difficult than that in SISO-NOMA system[7].The ergodic sum-rate gain of NOMA over OMA was demonstrated by [8] for single-antenna and multi-antenna uplink cellular networks.To date,NOMA has not been standardized in last new radio (NR) version of 3GPP Release 16.However,NOMA has been promoted into the stage of study item and is promising to be standardized in the B5G/6G version [9–11].In this paper,we aim at studying an effective and novel transceiver strategy in uplink multi-antenna NOMA system with error propagation aiming at reducing the transmit power consumption.

1.1 Related Works and Motivations

In the existing multi-antenna NOMA transmission schemes,the cluster-specific beamforming is widely used due to its easy implementation.Conventionally,by exploiting the channel information,the users of a multi-antenna NOMA system are organized into multiple clusters such that the users of the same cluster are served in the same space dimension[12,13].To handle the co-channel inter-cluster interference,the BS simply uses the zero-forcing beamforming relying on the channel matrices of the stronger users of each cluster in such a way that the stronger users become less interference-limited.In such situation,the channel realizations of the users in the same cluster should be highly correlated,which indicates that the system performance is sensitive to the correlation of the channel matrices/vectors.In[14,15],multiple beamforming vectors are generated randomly at the BS.In each beam,a cluster of users are served in the NOMA mode.At the terminals,the inter-cluster interference is suppressed by equipping with an interferencerejection equalizer,and then an SIC device is employed to remove the intra-cluster interference.Since the generation of beamforming vectors does not consider any information about user channels,it leads to that the equivalent channel strengthes between some users and the BS are quite small.Thus,in order to satisfy the minimum transmission rates of these users,it requires a large power consumption.When a unit matrix is served as the precoder,the receiving vector for each user is carefully devised to minimize the total transmit power in[16].

However,the existing schemes developed in [12–16] are applicable into the downlink NOMA system only.In the multi-antenna NOMA uplinks,the transmission strategy and the order of SIC is fundamentally different from those in the downlink.A new concept of signal alignment(SA)is conceived to design an uplink MIMO-NOMA transmission scheme in [17].To be specific,all users are separated into multiple clusters in the above SA-NOMA method,in each of which,a weak user and a strong user are included.The intention of precoding designed at the users is to align the channel vectors in each cluster into the same direction.At the BS,a zero-forcing receiver is leveraged to remove the inter-cluster interference and the SIC is used to facilitate the signal detection for the users in the same cluster.Unfortunately,the channel directions of two clusters may be quite close in the spatial domain for the above SA-NOMA scheme.In this situation,there will be a large loss of the useful signals when the signals pass through the interference-rejection equalizer.In a word,the shortcomings of this approach is that the power efficiency is degraded.It has a couple of reasons.On one hand,the transceivers of the users and the BS are not jointly designed.On the other hand,the clustered pairs lack of flexibility in dealing with various system conditions.Besides,in[18],an effective precoding design was proposed for uplink MIMONOMA system with group detection.By using zeroforcing equalizer,the precoder was obtained by an iterative update procedure.For two-cell uplink scenario,a two-tier methodology was developed to power minimization problem for MIMO-NOMA system with orthogonal space-time block code[19].

In addition,the existing works [12–17] mentioned above focus on the NOMA decoding with perfect SIC.In the practical NOMA system,error propagation caused by imperfect SIC has an adverse effect on the user signals decoded later.Thus,the consideration of error propagation is more meaningful in the design of NOMA scheme.Following the clusterbased design framework,the power allocation coefficients and the transmit beamforming are jointly designed to reduce the total power consumption and maximize the weighted sum rate with the consideration of error propagation [20].In [21],a joint pilot and payload power allocation method was developed for MIMO-NOMA uplinks with the consideration of error propagations and maximum ratio combining equalizers,in which geometric programming was invoked to maximize the weighted average signalto-interference-plus-noise ratio.Besides,both the ergodic rates and the outage probabilities are derived in the closed-form expressions for multi-antenna NOMA system in the presence of error propagation [22].By utilizing the theoretical results,the transmit power coefficients are designed in order to boost the user fairness of each cluster.However,it has the disadvantages of large power consumption in the cluster-specific beamforming.In this work,a power minimization problem is investigated in multi-antenna NOMA uplinks.For the reasons above,we develop a new multigroup NOMA scheme for the uplink MIMO-NOMA system with error propagations,where all users located in the cell coverage are separated into several groups.The inter-group interference is eliminated by invoking a new SIC,whilst the design of power control and equalizers aims at mitigating intra-group interference.

1.2 Contributions

Currently,high power consumption is an important issue for information and communications technology (ICT) industry.Therefore,it is urgent to design more power-efficient approaches to reduce carbon dioxide emission.Motivated by this observation,we intend to design an efficient MIMO-NOMA transmission scheme to reduce the power consumption for next generation communication systems.In summary,the main contributions of this paper are enumerated below.

1.A novel framework with group-based cooperative optimization is proposed for the uplink multiantenna NOMA system.A hybrid operation of SIC and parallel interference cancellation is equipped in the new multi-antenna NOMA framework.Specifically,the equalizers and power control are jointly optimized to suppress intragroup interference for the users in the same group,whereas the users in the different groups are served following the NOMA principle and the group-based SIC is invoked to remove the intergroup interference.

2.Different with the user-level SIC in the clusterbased NOMA scheme,the group-based SIC is conceived in this paper.In the conventional cluster-based NOMA method,the active users are separated into several clusters.The different clusters are served by using the space division multiple access (SDMA),while the users in the same cluster are detected by leveraging the user-level SIC.This NOMA framework has shortcomings of degraded power efficiency because the transceivers are not jointly designed and the inter-group coordination is not considered.However,in the proposed group-based SIC method,all users are divided into multiple groups according to average path losses.The users messages in the same group are decoded and subtracted simultaneously by adopting group-based SIC.The advantage of the proposed group-based SIC framework is that the transceivers in each group can be optimized jointly by taking intra-group and intergroup interference into consideration,and therefore the power efficiency can be enhanced.The comparison between the proposed group-based SIC NOMA with the conventional cluster-based NOMA is presented in Table 1.

Table 1.Comparison between different methods.

3.A power minimization problem is formulated under the constraint of per user’s minimum transmit rate.In the problem formulation,the effect of error propagation is considered from the perspective of practice.By using the relationship between the equalizers and the transmit power coefficients,the original joint optimization problem is converted into a simplified power control problem.In addition,a parallel iteration algorithm is devised to obtain the optimal transmit power factors.In simulations,it is shown that the proposed scheme outperforms both the conventional OMA scheme and the cluster-specific beamforming scheme.

1.3 Paper Organization and Notation

The remainder of this paper is organized as follows.In Section II,the system architecture of multi-group NOMA transmission is presented.The optimization problem of the equalizer and the transmit power is formulated and then transformed in Section III.Section IV proposes a parallel iterative power control scheme.Numerical results are then presented for validations in Section V.This work is concluded in Section VI.

Notation: The following notations shall be adopted throughout this paper.The uppercase and lowercase boldface letters denote matrices and vectors,respectively.XT,XH,X−1and X1/2stands for the transpose,conjugate transpose,matrix inverse and Hermitian square root of matrix X,respectively.Tr(·),det(·)and diag(·)refer to trace,determinant and diagonalization operations,respectively.represents the Euclidean/Frobenius norm of a vector/matrix.EA{·}denotes the operator of the expectation taking over random variableA,and the subscriptionAis sometimes omitted without leading to ambiguity.Cm×nis the set ofm × n-dimensional complex matrices.CN(µ,Σ) denotes the distribution of a circularlysymmetric complex Gaussian (CSCG) random variables with mean vectorµand covariance matrix Σ.0n,1nand Inrepresent ann×1 all-zeros vector,ann ×1 all-ones vector and ann × nidentity matrix,respectively,and the dimensionalitynis sometimes dropped out for convenience.The symbol i=refers to the imaginary unit.Re{·}represents the real part of a complex number.∪(·) stands for the union operation.represents Fox’s H-function.Any other notations are deferred to define in the place where they appear.

II.SYSTEM MODEL

In this paper,a macrocell with the coverage radius ofRBis considered,where the BS is located at the center of the coverage and there areUusers distributed in the coverage randomly with the near-field distanceRN.The number of antennas at each user and the BS are 1 andAR,respectively.The users are separated intoKgroups based on the propagation distances to the BS,and the number of users in them-th group is denoted byUm.Hereafter,for convenience,then-th user in them-th group is referred as UEm,n.Each user sends one data stream to the BS.Besides,the total number of active users using the same resource block is larger than that of antennas at the BS,i.e.,

whereUmdenotes the number of users in them-th group.If the condition (1) does not hold,the system is degraded into a traditional multi-user OMA system,which is not the focus of our paper.

2.1 The Criterion of User Grouping

In the proposed NOMA scheme with multi-group,all users’messages in the same group are decorrelated by the joint design of equalizers and power allocation,whereas the users in different groups are scheduled on the common resource block by using the NOMA method.The user grouping criterion depends on two factors: (i) the total number of concurrent streams per group,and(ii)the propagation distances from the users to their connected BS.

Firstly,the total number of concurrent streams in each group should not be more than the number of the BS’s receiving antennas,i.e.,

which ensures that the messages for users in each group can be decorrelated in parallel.

Secondly,the propagation distances are increased with the group index,i.e.,the users in 1st group have the smallest average distances to the BS,and then on.Letrm,ndenote the distance between the UEm,nand the BS.Then,we have

An illustration of system architecture and user grouping in this work is demonstrated in Figure 1.In this paper,the user group scheme is based on the propagation distances.The limitation is that there may exist the case that the users assigned to the different groups have a strong channel correlation,which will degrade the system performance.In the future,we will design more efficient user grouping method by taking the channel correlation into account.

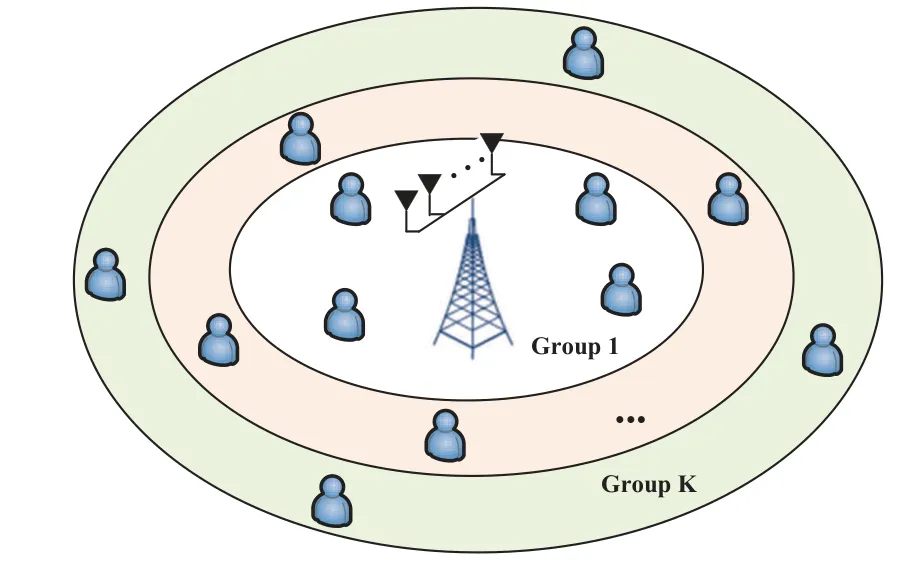
Figure 1.An architecture of multi-antenna NOMA transmissions with multiple user groups.

2.2 The Expression of Received Signals

In the considered model,multiple users transmit different messages to their associated BS at the same resource block.The signal received at the BS,z,is expressed as

where qm,urepresents the channel vector between the UEm,uand the BS,ωm,uandsm,uare the transmit power coefficient and the transmit signal of UEm,u,respectively,and v is the noise vector with each element following a complex Gaussian distribution of zero mean and variance.The channel vector can be characterized by a product of the small-scale and the large-scale fading,i.e.,

whereβstands for the path loss exponent,and each element in fm,ufollows a complex Gaussian distribution with zero mean and unit variance independently.

To facilitate the group-level power control and equalizer design in the next section,we rewrite the received signal into a form of matrices,which is given by

where Gmis named as the equivalent channel matrix between the BS and them-th group,the diagonal elements of Γmdenote each user’s transmit power coefficient of them-th group,and smis the stacked transmission signal for the users belonging to themth group.

2.3 Data Detections

Because the 1st group has the maximum average received signal strength,the signals of the users in the 1st group are detected in the first place at the receiver.Before decoding user signals in the 2nd group,the signals in the 1st group are cancelled from the composite signals,and so on,until the messages in theK-th group are detected.In the presence of multiple antennas at the BS,the channels are in the form of vectors.Thus,it is hard to sort the channels like the case with a single antenna.Currently,the optimal detection order in multi-antenna NOMA system is still an open problem.In the multi-antenna NOMA system,it is more complicated to sort the channels because the equalizer can also reshape the channel conditions.Commonly,the path loss or the propagation distance is used to determine the detection order which reflects the average channel strength.In this paper,the detection order is determined by the average path loss for each group.In fact,for uplink NOMA systems,the detection order will not affect the feasibility of signal decoding for the users in each group.

Let Emdenote the equalizer of them-th group.Then,the post-processed signal of them-th group is given as

where imis the inter-group interference,including the interference stemming from the undecoded NOMA users and the residual interference caused by error propagations,which is given as

where Σjis a diagonal matrix representing the residual interference caused by error propagations of thej-th group.Due to the characteristics of error propagation of imperfect SIC,it is difficult to model the impact of imperfect SIC in a unified analytical fashion.It was reported in [23,24] that a linear function can effectively represent the relationship between the residual interference and the power of the received signal.Thus,it is common to use a so-called fractionalcancellation-error parameterϵto roughly account for all sources of SIC errors [23,24],in whichϵcan be obtained by long-term measurement.Therefore,Σjis defined as

whereϵj,urepresents the residual interference factor of UEj,u.

In the remaining,we will try to solve the joint design problem of the transmit powers and the equalizers,i.e.,{ωm,u,Em}.In doing so,the uplink channel state information(CSI)should be available,which can be achieved by channel estimation at the BS.When the design of power allocation is completed,the BS will deliver the optimal power coefficients to its associated users via downlink broadcasting channels.

Based on the decoded signals in (10),the UEm,u’s signal-to-interference-plus-noise-ratio (SINR) is expressed as

where[Em]:,ustands for theu-th column of the matrix Em,and Zmrepresents the covariance matrix of the inter-group interference,which is written as

III.PROBLEM FORMULATION AND TRANSFORMATION

Green communication is one of the main themes for future communications.In this work,the optimization problem is formulated as a sum power minimization problem.In particular,under the conditions that each user’s quality of service (QoS) and maximum transmit power are satisfied,our objective is to reduce the transmit power consumption.The optimization problem can be formulated as

wherePmaxandare the maximum allowed transmit power and the minimum transmit rate of UEm,u,respectively.Due to the fact that the 1st constraint in the optimization problem is non-convex,the problem(Q1)is non-convex obviously.In such case,obtaining the optimal solution is quite difficult.By using the relationship between the optimal equalizer and the transmit power,the original problem(Q1)will be transformed in the following.In the considered uplink NOMA scenario,the minimum transmission rate is included in the constraint (16),which ensures the successful decoding and SIC at the BS.Thus,the SIC decoding is not considered in the optimization problem,which is different from that in the downlink NOMA system[25].

In terms of maximizing each user’s SINR performance,the minimum mean square error (MMSE)equalizer is proved to the best linear equalizer [26].Therefore,the MMSE equalizer of them-th group is expressed as

It is worth mentioning that when the messages of the previous groups are decoded,the recovered data will be subtracted from the received signal at the BS rather than the equalized signal.As a result,the equalizer in(18) will not include the equalizers of the previously decoded groups.

By substituting (18) into (13),the SINR of UEm,ucan be further given by

Therefore,the original optimization problem (Q1)is transformed to

It is shown that the joint power control and equalizer optimization problem (Q1) is transformed to a pure power control problem.In problem (Q2),the optimization variables are all users’ transmit powers.In fact,there arevariables in total.It can be observed from the SINR expression in (19)that the transmit power of the users in the same group and the different groups are highly coupled,which is related to the first and the second terms in the inversion operation.The first constraint in problem (Q2)is still non-convex.Thus,the problem (Q2) is nonconvex.Thus,it is still not easy to address this optimization problem.In the next section,we will focus on addressing the power control problem(Q2).

IV.POWER CONTROL DESIGN PROCEDURES

In this section,a group-level transmit power optimization scheme is proposed,in which the transmit power of each group is optimized iteratively.In the design of the transmit power of them-th group,the transmit power in other groups is fixed.

Proposition 1.In order to characterize the effect of any other user’s transmit power,,on the SINR ρm,u,we define a new function as

Proposition 2.Only when the equalities in the 1st constraint of the problem(Q2)hold,the optimization problem achieves the optimal solution.Then,we have

Proof.This proposition is proved by invoking the contradiction.Supposeis the optimal solution of the optimization problem (Q2),and an inequality holds for an arbitrary user,e.g.,

Based on the Proposition 2,we develop an iterative power control scheme as

wherekandtare the indices of the outer and inner iterations,respectively.When designing the power control scheme of them-th group,the inter-group interference Zmis constructed.For the inner iteration,the initial value is set as the optimal value of the last outer iteration.

Proposition 3.When the initial transmit power is feasible,the transmit power of each user is decreased with the iterations.Accordingly,the proposed power control scheme can convergent to a stationary point.Besides,the 2nd constraint is satisfied automatically.Proof.By substituting the transmit power into the QoS constraint,we have

where the 1st inequality holds by using the Proposition 1.Thus,it can be derived that

Thus,if the initial transmit power is feasible,the proposed power control scheme can convergent to a stationary point.Besides,the 2nd constraint is also satisfied,i.e.,

The implementation procedures of the proposed power control scheme are presented in Algorithm 1.

After the users’transmit powers in each group is optimized,we can get the optimal equalizers{Em}at the BS by substituting the optimized transmit power into(18).

Remark 1.It is noted that when the channel correlations for the users in the same group are strong,there will be large intra-group interference in data detection for the proposed group-based SIC scheme.However,in the conventional cluster-based NOMA scheme,a preferable performance is achieved under the condition that the channels of users in the same cluster should be highly correlated,which implies that the system performance is sensitive to the correlation of channel realizations.In practice,when the number of active users organized on the same resource block is not large,it is hard to find two channel vectors with high correlation in the system,which will degrade the performance of conventional cluster-based NOMA method.Besides,it seldom appears that two channels have high correlation in the same group.The performance comparison between the group-based SICscheme and the conventional cluster-based NOMA scheme will be presented later.

V.NUMERICAL ANALYSIS

In this section,the total transmit power of the proposed algorithm is evaluated.The simulation parameters are presented in Table 2.In order to compare with the existing methods,two conventional methods are introduced,i.e.,(i)Cluster-based scheme: All users are organized into multiple clusters based on the channel directions,and there are two users in each cluster.At the BS,the interference rejection receiver is used to suppress inter-cluster interference;(ii)The optimal OMA scheme: The different groups are served in different slots with the same time durations,and the MMSE equalizer and the optimal power control scheme is adopted.In this paper,in order to make a fair comparison with the existing cluster-based scheme,the number of SIC layers should be equal for all schemes.Thus,we set the number of groups is 2 in simulations.It is worth mentioning that the proposed scheme is also applicable to the scenario with arbitrary number of user groups.

Table 2.Simulation parameters.

5.1 The Effect of Minimum Rate Requirement

Figure 2 depicts the total transmit power for different rate requirements.It is shown that as the rate requirement increases,the power consumption is also increased.Besides,the proposed scheme is superior to the two benchmarks in terms of the power consumption.Particularly,the performance gap between the OMA scheme and the proposed one becomes larger with the rate requirement because of the benefits of NOMA over OMA.It is observed that the clusterbased NOMA scheme has the worst performance.It is partly because the user channels in the same cluster are not highly correlated when the number of users is not large,and partly because the useful signal power is weakened in suppressing the inter-cluster interference when the channel directions of different clusters are similar.Thus,it means that the conventional clusterbased scheme is sensitive to the error propagations,whereas the proposed design scheme is robust in the case of imperfect SIC.In this paper,we consider the scenario that the number of users is not large.Thus,it seldom happens that the users in different groups have strong channel correlation.It is also the reason that the performance of the proposed scheme is better that the existing ones substantially.In the scenario that the number of users is huge,user scheduling can be used to avoid the terrible situation that the users in different groups have strong channel correlation.

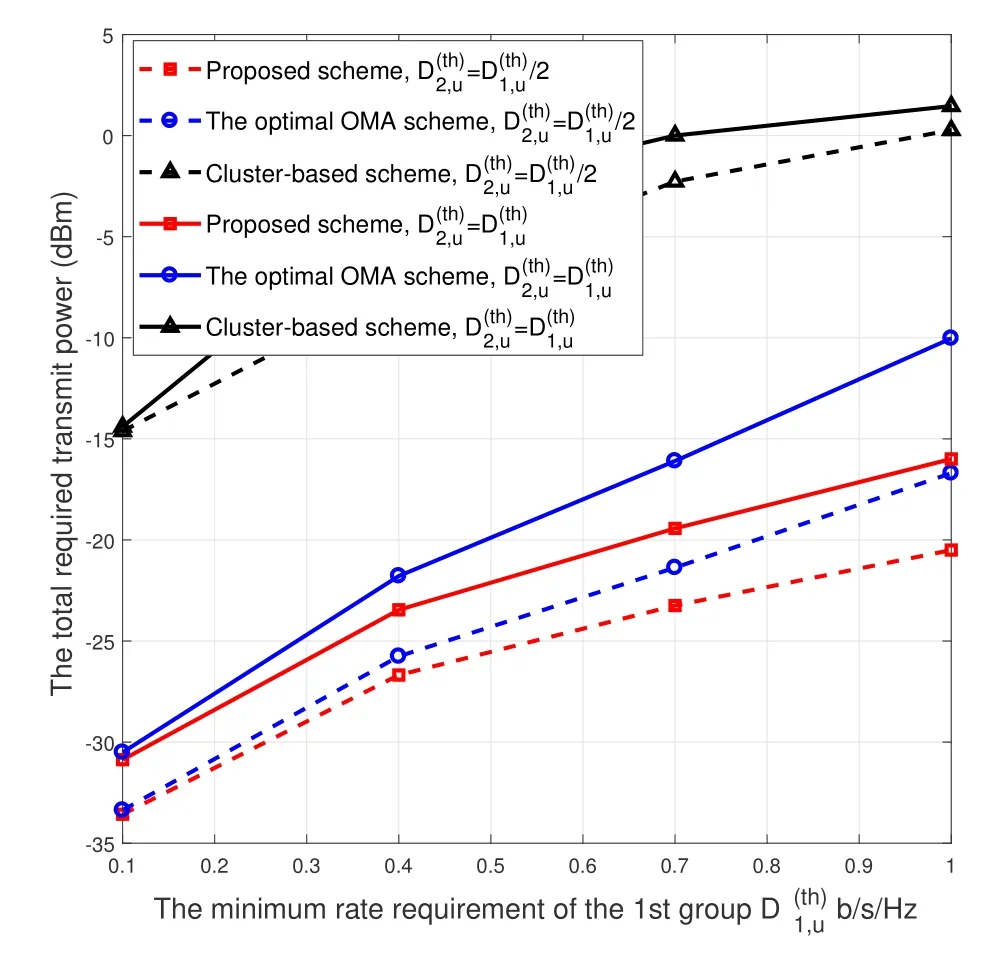
Figure 2.The total transmit power versus the minimum rate requirement with ϵ=0.01.

5.2 The Effect of Error Propagation Factor

Figure 3 depicts the total transmit power for different error propagation factors.It is shown that for the proposed schemes,the required transmit power is increased with the error propagation factor.The reason is that the inter-group interference grows with the error propagation factor.Thus,for the sake of achieving the predefined SINR thresholds,the transmit power should be improved.However,when the error propagation factor is not so large,the proposed scheme has the least power consumption compared with the benchmarks.The reasons have been given in the forgoing analysis.As the error propagation factor increases,the difference of power consumption between the proposed scheme and the OMA scheme is decreased.It indicates that the benefits of NOMA fades away when the error propagation is serious.Based on the curve behaviors in Figs.2-3,it is clear that the proposal is capable of reducing the total transmit power considerably compared with other existing methods,which is promising for the future cellular communication networks.

Figure 3.The total transmit power versus the residual interference factor with =1 b/s/Hz.

VI.CONCLUSION

In this work,the equalizers and the power control are designed jointly aiming at minimizing the total power consumption for uplink multi-antenna NOMA system.Importantly,the design framework with group-based SIC is developed and the error propagation stemming from imperfect SIC is considered for the developed framework.The proposed NOMA scheme with groupbased SIC is capable of dealing with the intra-group and the inter-group interferences effectively.Besides,an optimization problem is developed to realize the objective of low-power transmission.In order to address the joint optimization problem,the original problem is converted into a simplified power control problem,which is further solved by a parallel iteration method.It is demonstrated by simulation results that the total transmit power of the proposed group-based SIC scheme is less than that of the conventional clusterspecific NOMA scheme.The improvement percentage increases with the minimum rate requirement.In the future,we will investigate the low-power transmission scheme for MIMO-NOMA system with imperfect channel state information.

ACKNOWLEDGMENT

This work was supported in part by the National Natural Science Foundation of China under Grant 62171235 and Grant 62 171237;in part by the Qinglan Project of Jiangsu Province;and in part by the Open Research Foundation of National Mobile Communications Research Laboratory of Southeast University under Grant 2023D01.