Discrete Phase Shifts Control and Beam Selection inRIS-Aided MISO System via Deep Reinforcement Learning

Dongting Lin,Yuan Liu

School of Electronic and Information Engineering,South China University of Technology,Guangzhou 510641,China

Abstract: Reconfigurable intelligent surface (RIS)for wireless networks have drawn lots of attention in both academic and industry communities.RIS can dynamically control the phases of the reflection elements to send the signal in the desired direction,thus it provides supplementary links for wireless networks.Most of prior works on RIS-aided wireless communication systems consider continuous phase shifts,but phase shifts of RIS are discrete in practical hardware.Thus we focus on the actual discrete phase shifts on RIS in this paper.Using the advanced deep reinforcement learning(DRL),we jointly optimize the transmit beamforming matrix from the discrete Fourier transform(DFT)codebook at the base station(BS)and the discrete phase shifts at the RIS to maximize the received signal-to-interference plus noise ratio (SINR).Unlike the traditional schemes usually using alternate optimization methods to solve the transmit beamforming and phase shifts,the DRL algorithm proposed in the paper can jointly design the transmit beamforming and phase shifts as the output of the DRL neural network.Numerical results indicate that the DRL proposed can dispose the complicated optimization problem with low computational complexity.

Keywords: reconfigurable intelligent surface;discrete phase shifts;transmit beamforming;deep reinforcement learning

I.INTRODUCTION

Nowadays,reconfigurable intelligent surfaces (RIS)have aroused wide concern due to its low cost,ease of deployment and directional signal enhancement[1–3].RIS consists of a large number of reflecting units,each of which can independently reflect the incident signal in the desired direction through different phase shifts.RIS can obtain better propagation conditions by adjusting the dynamic change of phase shifts.Moreover,benefiting from breakthroughs in programmable metamaterials manufacturing,the RIS has been regarded as one of the crucial technologies for the sixgeneration(6G)wireless communication systems,enabling communication systems to expand beyond massive multiple-input multiple-output(MIMO)and realizing smart radio environments[3–9].

1.1 Related Work

There are many works to optimize the performance of wireless communication systems with RIS-assisted.In uplink RIS-assisted MIMO system,matched filter (MF) and the optimal receiver were researched in[7].In[10],the transmit beamforming and phase shift were jointly optimized to maximize the security rate of RIS-assisted MIMO system using alternating optimization and semidefinite relaxation methods.An algorithm for optimizing the transmitted beam covariance and the phase shift matrix was investigated in[11].A joint optimization problem of phase shifts and transmit beamforming was investigated in[12]for multiple-input single-output(MISO)systems using alternating optimization.The similar problems for RISaided MISO systems were studied based on manifold optimization methods[13].

However,the above mentioned works were based on the assumption of continuous phase shifts of RIS.In reality,it is impractical to implement continuous phase shifts for RIS by current hardware,thus the phase shifts of RIS should be discrete in practice[14,15].Due to the high non-convex nature of joint optimization phase shifts and transmit beamforming,most of the work was to use the alternating optimization method to gain the optimal results of phase shifts and transmit beamforming alternately [16].On the other hand,thanks to the development of deep learning(DL) which is able to solve very complicated problems,the work [17] and [18] used DL methods for continuous and discrete phase shifts design.Note that DL is supervised learning that requires collecting mass data for training.In addition,labels of data are hard to obtain,however,unlike DL,deep reinforcement learning(DRL)does not require labels during training and is an online learning under the real-time generated data,which can dispose complicated optimization problems with low computational complexity in wireless communications without collecting mass training data [19].By receiving rewards from the environment,DRL is able to find solutions to complex optimization problems for wireless communication systems,enabling efficient algorithm design [20].As a result,DRL has also been used to design RIS-aided wireless communication systems [19–30].Note that the DRL based work all considered continuous phase shifts.

1.2 Contributions

In the paper,we propose the joint optimization problem of BS beamforming and phase shifts of RIS.Unlike the prior work considering continuous designs,our paper considers discrete design for both phase shifts of RIS and BS beamforming.In particular,based on the limited channel state information (CSI)feedback that only requires a few bits in uplink,a codebook-based BS beamforming scheme is adopted.The following are the main contributions summarized of our work:

• We investigate a joint problem of transmit beamforming based on the DFT codebook and the discrete phase shifts of RIS in multiuser downlink MISO systems.

• As the studied problem is non-convex because of the coupling between discrete variables,the DRL algorithm is applied to dispose the non-convex optimization problem,in which a double deepQlearning network (DDQN) is carefully designed to accommodate the considered problem.

1.3 Organization and Notations

The rest of the paper is arranged as follows.Section II describes the system model and the establishment of mathematical.In Section III,a joint design algorithm of transmit beamforming and phase shift based on DRL is proposed.Simulation results are demonstrated in Section IV to evaluate the performance of the proposed algorithms,whereas we summarize the paper in Section V.

The notations used in this paper are listed as follows.Cm×nrepresents the space ofm×ncomplexvalued matrices.For a complex-valued vectorn,||n||,diag(n),andnHdenote its Euclidean norm,a diagonal matrix with each diagonal element being the corresponding element inn,and conjugate transpose,respectively.Scalarnkrepresents thek-th element of a vectorn.For any matrixB,BH,andBm,ndenote its conjugate transpose,and(m,n)-th element.jrepresents the imaginary unit,i.e.,j2=−1.For a complex-valued scalarn,arg(n)and|n|represent its phase and absolute value.

II.SYSTEM MODEL AND PROBLEM FORMULATION

2.1 Communication Network Model

In this paper,we focus on a MISO wireless communication system making up of a uniform linear array(ULA) ofMantenna units deployed in a BS andKsingle antenna users,as shown in Figure 1.The RIS is deployed withN=Nx×Nyphase shifters,whereNxandNyare the number of reflection units per column and row of the RIS,respectively.RIS uses controllers to change the phase of each reflection unit in real time according to the communication propagation environment.Considering the path loss caused by signal propagation and reflection,this paper ignores the case of signal reflected through RIS twice or more times.On the other hand,in order to research the effect of joint optimization of transmitting beam based on codebook and discrete phase shift on the performance of RIS assisted wireless system,it is assumed that all channels fit the quasi-static flat fading model.

Figure 1.The model of RIS-aided multiuser wireless communication system.

We defineynas the signal after incident signalxnis reflected by then-th reflection unit of the RIS,whereynis represented byxnas follows:

where the reflection amplitude coefficient and phase shift coefficient areβn ∈[0,1] andθn ∈[0,2π]for then-th reflection element of RIS,respectively.Θ=represents the diagonal reflection matrix from the incident signal to the reflected signal throughNreflection units of the RIS,i.e.,y=Θx.

In general,we assume that the reflection coefficient vector of the RIS isv=[v1,...,vN],such thatβn=|vn|andθn=arg(vn)for then-th RIS unit.It is worth mentioning that in practical reflection models,the amplitude coefficients of reflection vary with the phase shifts [28].Thus,this paper considers to use a practical reflection model to gain the reflection amplitude coefficient according to the phase shift.Moreover,due to the actual RIS hardware construction,we consider that the phase shift is discrete variable [31].LetLdenote the number of phase shift quantization levels,andbrepresents the number of bits,whereL=2b.For convenience,the paper assumes that the discrete phase-shift value is gained through uniformly quantizing the interval [0,2π).Therefore,the discrete value set of each reflection unit is expressed as

It is important to note that forNreflection units withLnumber of phase shift quantization levels per reflection unit,the total number of phase shift patterns isLN.

LetC1×N,C1×M,andG ∈CN×Mrepresent the channels from the RIS to userk,the BS to userk,and the BS to RIS,respectively.At the BS,we set up a predefined codebook known to both users and the BS,from which each user can select precoding vectors[32].In this paper,the discrete Fourier transform (DFT) codebook is used,which is efficient for spatially correlated channels produced by ULA and is proved to approximately match the optimal beamforming vectors[33,34].As shown in Figure 2,the pre-designed codebook contains a list of transmitter and receiver codewords,each of which reflects one state of the channel at a given time.When the user selects the beamforming vector that is to maximize its SINR after estimating its CSI,the corresponding precoding matrix indicator (PMI) is sent to BS.In order to make the set of DFT codevectors evenly distribute over the whole beam directions,the unified DFT codebook is adopted[33].The unified DFT codebook with sizeZfor ULAs withMantenna units is expressed byM ×ZmatrixW=[w0,w1,...,wZ−1],where thez-th codevector is

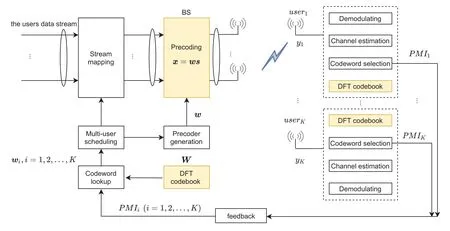
Figure 2.The feedback beamforming of the multiuser MISO system.

wherenkis the zero mean additive white Gaussian noise(AWGN)with entries of variance.The SINR of userk=1,...,Kis then expressed as

2.2 Problem Formulation

Based on the above description,we focus on maximizing the total received SINR by selecting the transmit beamformingwand phase shift vectorθthrough joint optimization.Therefore,its optimization problem can be formulated as

Due to the coupling of discrete variables,(P1) is a complex non-convex optimization problem.If the method of exhaustive search is used to dispose the optimization problem,it has a high complexity ofO(ZKLN).To reduce the complexity of solving the optimization problem,a DRL based approach is introduced in the next section.

III.DEEP REINFORCEMENT LEARNING BASED OPTIMIZATION SCHEME

Unlike DL,DRL based methods avoid huge training labels and have the property of online learning and sample generation,which can dispose complicated optimization problems with low computational complexity without collecting mass training data.In this section,we first briefly introduce the DRL techniques and then describe the proposed DDQN based framework in detail.

3.1 Brief Preliminaries of DRL

DRL includes many learning frameworks,among which DQN learning framework stores historical sample data through the experience gained in the learning environment:{st,at,rt,st+1}.The rewardrtand the newly gained statest+1enter the target network to get the new targetQvalue:

Since the DQN selects the actionat+1according to the next statest+1,the parameters of the consistent neural network training model can predict theQ(st+1,at+1) value,which may lead to overoptimistic estimation of the value function.Based on this problem,this paper considers the double deepQlearning network(DDQN)learning framework,which can decouple the action selection and action state values,and enable the two networks to learn independently without affecting each other.The calculation formula of targetQvalue based on DDQN learning framework is expressed as:

It can be seen from Eq.(12)that DDQN calculates the targetQvalue by using the parameters of two different networks,namely,parameterθtof the currentQnetwork and parameterof the targetQnetwork.The currentQnetwork is mainly used for action selection,and the targetQnetwork is mainly responsible for calculating the targetQvalue.In the general DDQN learning and training process,oneQnetwork is adopted to get the action of the next time stepat+1,and another network is utilized to get the estimatedQvalueQ(st+1,at+1),thus decoupling the choice of action and the estimation of state value is realized.

3.2 DRL-Based Scheme Design

DRL consists of two major parts,i.e.,the agent and the environment.We set the communication system as the environment and the agent is independent of the environment.As we can see from Figure 3,these two parts complement each other.The agent performs learning algorithm according to the feedback reward of the environment,and the action state value obtained by the learning algorithm further guides the environment to finally achieve the best balance state.As shown in Figure 3,the agent in the DDQN learning framework uses theϵ-greedy strategy to learn the network and can make decisions to select the corresponding action by learning decision strategy from exploration experience.The corresponding elements are shown as follows.

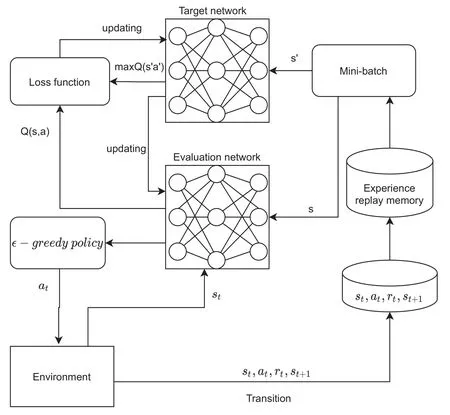
Figure 3.The DDQN framework for an RIS-aided wireless communication network.

• State space: During time stept,we define the statestas the collections of RIS phase-shifts and transmit beamformers,i.e.,

• Action space: The agent takes the current state as the input of the neural network and updates the phase shift and transmit beamformers according to the reward feedback.When the network has been updated,new phase shifts and transmit beamformers are generated.Thus,the action vector is expressed as:

• Reward function: The optimization goal of this paper is to maximize the total received SINR.So we take the total received SINR as the rewardrt.

In the DDQN,the agent is able to obtain samples{st,at,rt,st+1}at each time step and randomly selectsUsample pairs from the experience pool when training the neural network.In the DDQN learning framework,the estimated network and the target network are designed to gain the estimated valueQEand the target valueQT(st+1,arg maxa QE(st+1,a)),respectively.Therefore,we update the estimated network parameters by obtaining gradient information via the Adam algorithm and the loss between the estimated network and the target network.The loss function of the proposed algorithm is expressed as:

After updating the estimation networkJtimes,we can copy the weight parameters of the neural network from the estimation network to the target network and update it.Algorithm 1 is the Pseudo code of DRL scheme proposed.

IV.NUMERICAL RESULTS

We show the simulation results to further verify the effectiveness of the proposed scheme in this section.

4.1 Simulation Setup

We focus on the Rician fading channel model to explain the LoS components of all the channels as[35,36]:

wheredr,k,dBI,dd,kare the communication transmission distances of RIS-user,BS-RIS,and BS-user links,respectively.According to the above formula,αr,αBI,andαdare the attenuation coefficients of the corresponding transmission channel,whereαr=2.5,αBI=2,αd=3.5.In addition,L0is the path loss at the reference distance ofd0,and we set the signal attenuation of all channels at a reference distance of 1 meter(m)to 10dB.

In the proposed DDQN learning framework,we consider that all neural networks have four layers,and the estimate network and target network apply Adam algorithm to update network parameters.The input layer and output layer both containN+Kneurons,and the two hidden layers in the middle are 200 and 300 neurons,respectively.Furthermore,we set the batchsize as 32,the learning rate 10−3,the discount factor 0.9,and the experience replay capacity 10000.

As shown in Figure 4,we set the distanceD0between BS and RIS as 30 m,and the users are located on the horizontal line which is parallel to the connection line between BS and RIS.The vertical distance of two parallel lines is set asDv=2 m,and we assume that the horizontal distance between the user and BS isDh.Therefore,we can obtain the distance expressions of BS-user and RIS-user respectively asDBU=

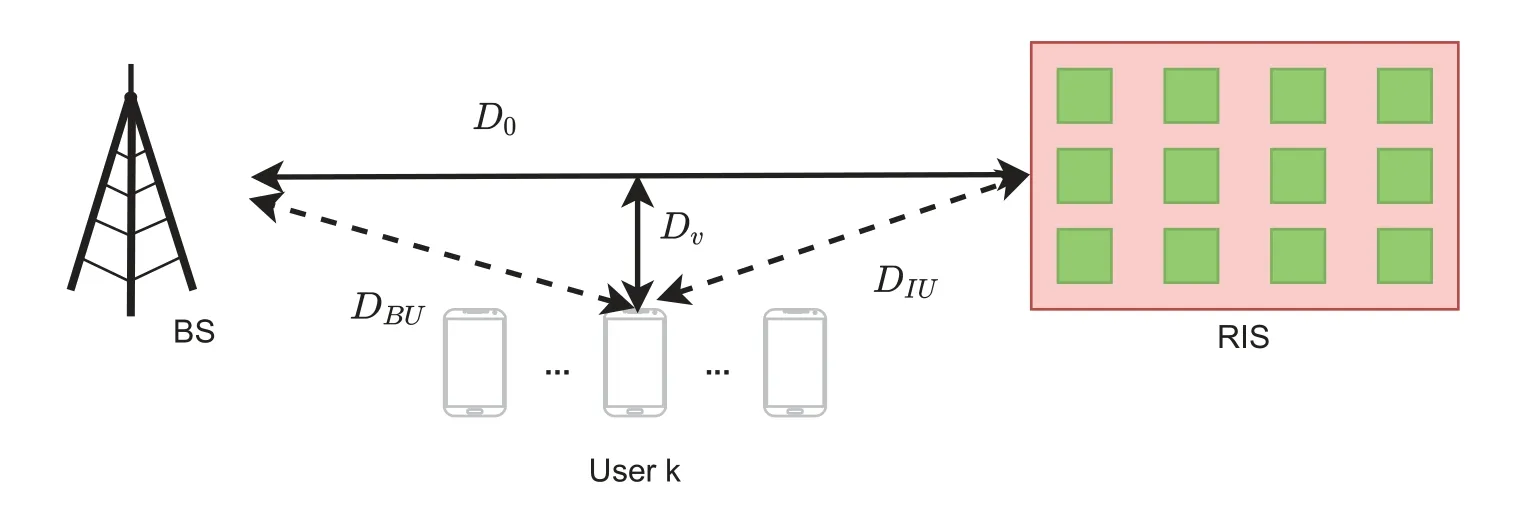
Figure 4.Simulation setup.

4.2 Results and Analysis

1)Figure 5 shows SINR versus training iterations for the proposed scheme.It is shown that the DDQN scheme can achieve approximately 5dB at the beginning,and converges to about 20dB after 25,000 training iterations.This result indicates that due to the high-dimensional space,the DDQN-based scheme needs many iterations to explore the environment and the convergence is not very stable during training.However,finally the DDQN algorithm can converge and obtain a solution because it can learn from the exploration experience.

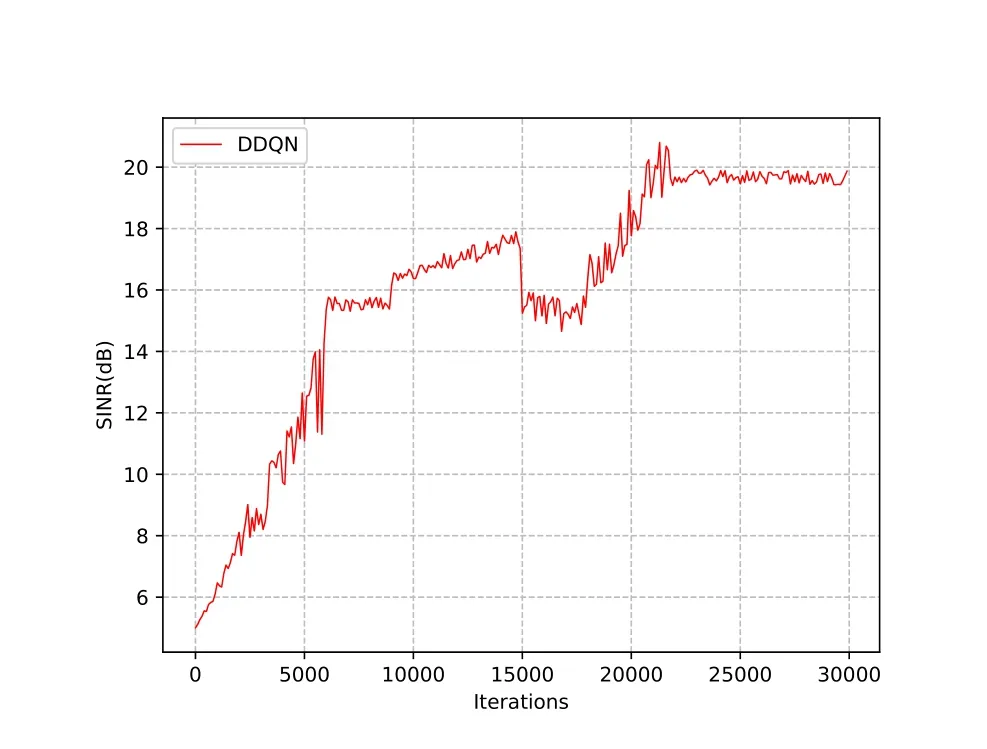
Figure 5.SINR versus training iterations.

2)In Figure 6,we compare the total received SINR of the system with 1-bit,2-bit,3-bit phase shifters and without RIS versusDh,whereM=5,N=9,andβmin=0.2.The value ofβminrepresents the curve of amplitude coefficient with phase shift [28].It can be found in the simulation result diagram that for the scheme without RIS,the total SINR first decreases and then increases with the increase ofDh,but when the user is close to RIS and away from BS,the total SINR tends to be stable without the assistance of the RIS.However,this problem can be partially solved by deploying RIS,which means that in an RIS-assisted wireless network,a greater distance between the user and the BS does not necessarily result in worse performance,because the user can receive signals reflected from the RIS.In addition,we find that the higher the number of quantized bits of the discrete phase shifts,the better its performance.This can be analyzed that because of discrete phase shifts,the multipath signals from BS including those reflected by RIS and those not reflected are not fully aligned at the receiver and the misalignment of multipath signals becomes more obvious on account of the low level of discrete phase shifts quantization,which leads to a loss of performance.

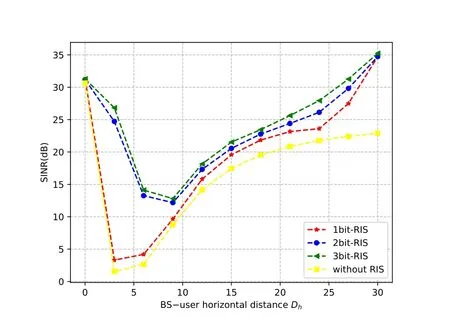
Figure 6.Received SINR versus BS-user horizontal distance,Dh.

3) As shown in Figure 7,we show the trend of the total SINR with the number of reflection elementsNat the RIS versus 1-bit,2-bit,and 3-bit phase shifters whenDh=15 m,M=5,andβmin=0.2,which is further verified the influence of quantization level of the discrete phases and the number of reflecting unitsNon RIS performance.We see from the corresponding graph that asNincreases,the performance of 1-bit phase-shift quantization scheme becomes stable but the 2-bit and 3-bit schemes still increase withN.This shows that the quantization bits play an important role in discrete phase-shift RIS.

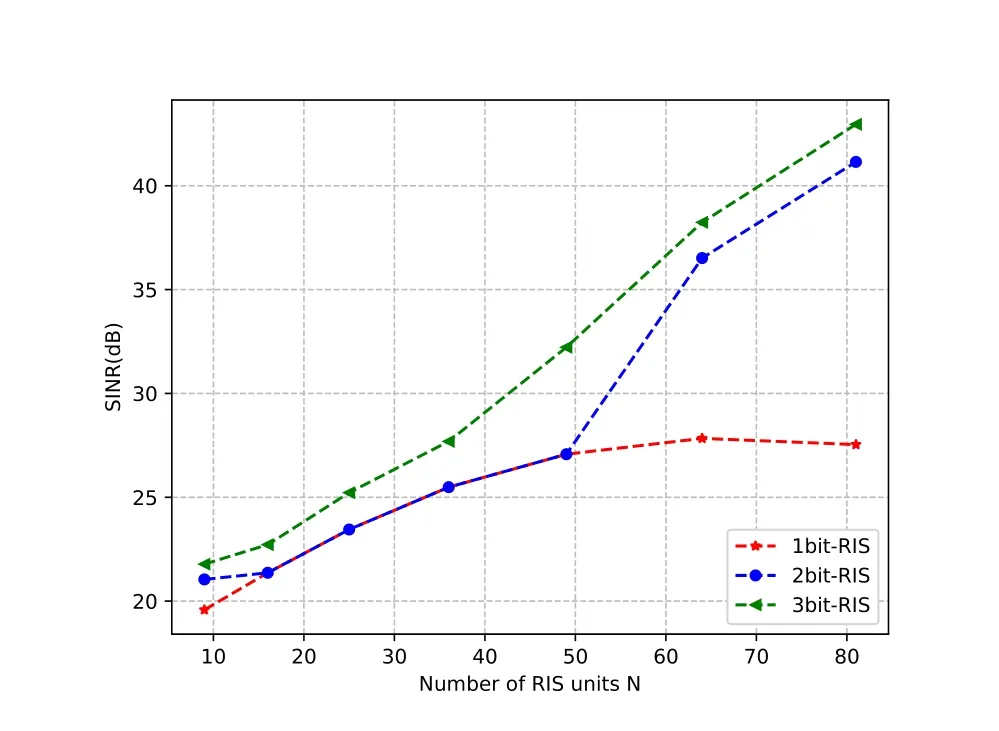
Figure 7.Received SINR versus the number of reflecting elements N with different quantitative level.

4)To understand the effect of ideal amplitude coefficients and actual amplitude coefficients on RIS performance,the total SINR versus the number of reflecting unitsNwithβmin=1,βmin=0.6,andβmin=0.2 is shown in Figure 8,whenDh=15 m,M=5,b=2.It can be analyzed from Figure 8 that asNincreases,the gap between the ideal case (βmin=1)and practical cases (βmin=0.6,andβmin=0.2)on performance becomes larger.Obviously,this result is shown that the closerβminis to the ideal case,the better its the performance is.In addition,it is shown that the signal loss is still not negligible even for largerβminvalue.The above results indicate that the consideration of RIS hardware defects is very important for beamforming design in practical application systems[28].

Figure 8.Received SINR versus the number of reflecting elements N with different βmin.

5) From Figure 9,we compare the influence of the number of BS antennas on the performance of the schemes proposed in this paper,whenDh=15 m,N=9,b=2,andβmin=0.2.We can observe that whether with or without RIS,the received SINR changes in triangular shape as the number of antennasMincrease,because the transmitted beam vector is selected based on DFT codebook,and according to the Eq.(3),we can see the relationship between the vector in DFT codebook and the number of antennasM.As the increase ofM,the transmitted beam vector will change periodically as the angle of trigonometric function,and the performance is increased with the RIS,and as shown in Figure 9,it presents a triangular periodic increasing state.The results verify the specific structure of the DFT codebook and the fact that RIS can reflect signals by phase modulation and shift,so as to realize energy efficiency and higher spectrum of wireless networks.

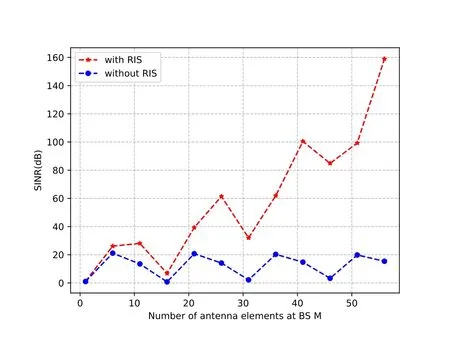
Figure 9.Received SINR versus the number of antenna element at BS M.

6) Finally,we simulate a multi-user system model and assume that multiple users are in the same line whenDh=15 m,N=9,M=5,b=2.Figure 10 shows the total SINR versus the number of usersK,for the case ofβmin=1,βmin=0.6,andβmin=0.2.It is shown that the total SINR goes up as the number ofKgoes up,because more users provide more diversity gain in the system.

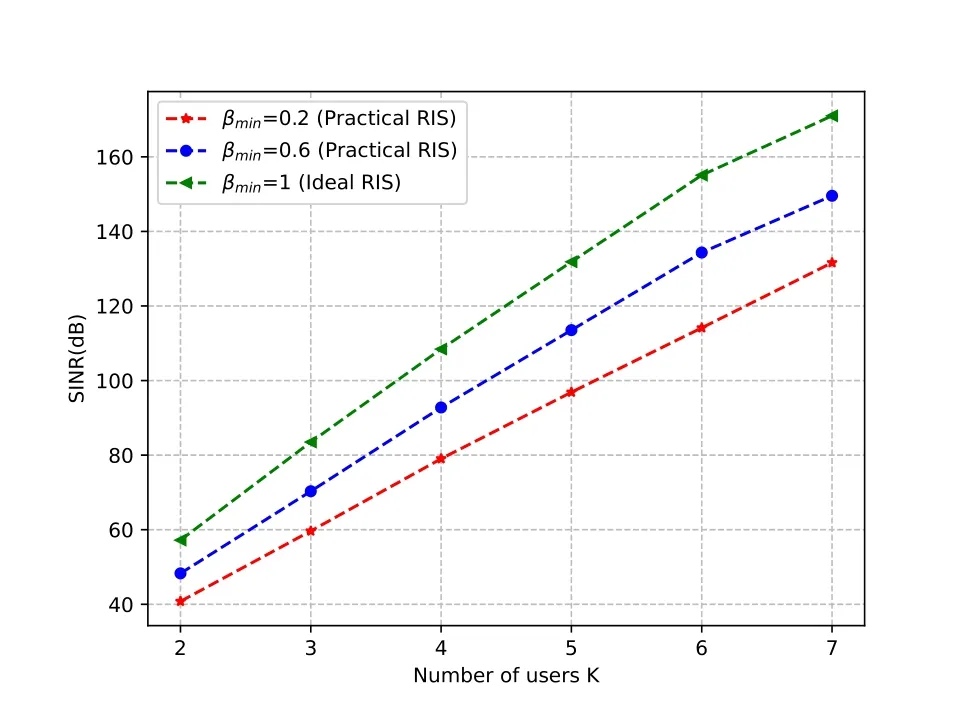
Figure 10.Received SINR versus the number of users K.

V.CONCLUSION

In the paper,we explored the received SINR maximization problem in RIS-aided wireless communications with joint transmit beamforming from the DFT codebook at the BS and practical discrete phase shifts at the RIS.We applied the DDQN learning framework,whose algorithm learns from the environment and obtains experience to map the relationship between previous and current optimization variables,which can dispose of the non-convex optimization problem proposed in the paper.We showed that the DRL method used in this paper can effectively solve the problem of combining multiple discrete variables.