Multi-Topology Hierarchical Collaborative Hybrid Particle Swarm Optimization Algorithm for WSN
2023-08-26YiWangKanqiWangMaoshengZhangHongzhiZhengHuiZhang
Yi Wang ,Kanqi Wang,2,* ,Maosheng Zhang ,Hongzhi Zheng ,Hui Zhang
1 School of Information Science&Technology,Northwestern University,Xi’an 710127,China
2 Institute of Artificial Intelligence,Xiamen University,Xiamen 361102,China
3 Institute of Disaster Prevention and Ecological Restoration,Xi’an Jiaotong University,Xi’an 710054,China
Abstract: Wireless sensor networks (WSN) are widely used in many situations,but the disordered and random deployment mode will waste a lot of sensor resources.This paper proposes a multi-topology hierarchical collaborative particle swarm optimization(MHCHPSO)to optimize sensor deployment location and improve the coverage of WSN.MHCHPSO divides the population into three types topology: diversity topology for global exploration,fast convergence topology for local development,and collaboration topology for exploration and development.All topologies are optimized in parallel to overcome the precocious convergence of PSO.This paper compares with various heuristic algorithms at CEC 2013,CEC 2015,and CEC 2017.The experimental results show that MHCHPSO outperforms the comparison algorithms.In addition,MHCHPSO is applied to the WSN localization optimization,and the experimental results confirm the optimization ability of MHCHPSO in practical engineering problems.
Keywords: particle swarm optimizer;levy flight;multi-topology hierarchical collaborative framework;lamarckian learning;intuitive fuzzy entropy;wireless sensor network
I.INTRODUCTION
The Wireless Sensor Network (WSN) is a multi-hop AD hoc network made up of a number of wireless sensor nodes and data processing programs [1,2].Each node in the WSN has the ability to be aware of its environment and can collect and process data in that environment.As a result,the location of nodes in the network is critical.An excellent network node deployment scheme can reduce the time of wireless sensor establishment,coordinate and control the communication state between network nodes,extend the network lifetime,and effectively adapt to changes in the environment.However,the optimal node deployment problem itself is an NP-hard problem,and evolutionary algorithms can often obtain approximate optimal solutions to such problems.
The heuristic algorithm has the advantages of excellent performance,simple implementation and strong generality[3,4].Therefore,it is widely used in a variety of engineering applications[5,6].Compared with other heuristic algorithms,PSO has the advantages of fewer parameters and strong convergence ability,so it is widely used in various practical applications.There are more than 46,000 citations.The application of PSO in different classification,function optimization,and regression tasks has not stopped [7–9].However,PSO also has some shortcomings: first,in the exploration stage,the convergence is too fast to explore the whole global space,and finally falls into local optimal;Second,the convergence speed of PSO is slow around the extreme point [10,11].The reason for this is that the algorithm oscillates around the optimal solution all the time due to the mismatched inertial weight,but cannot find the optimal solution directly.Therefore,many scholars proposed different methods to improve the performance of PSO [9,12].The first common improvement scheme is to mix PSO with one or more other algorithms[13,14].The second improvement is to use the multi-subgroup strategy.There are usually two ways to improve such algorithms: (i) Dynamic subgroup method,which dynamically adjusts the members in the subpopulation or adjusts the size of each subpopulation according to the search environment of the current individual[15,16].(ii)Staged multi-subgroup method,which divides the population into multiple subpopulations in the exploration stage and gradually merges the subpopulations with the progress of iteration[17].Both methods rely on multiple subpopulations to form multiple optimization centers so that the algorithm can obtain more global information in the early stage.Later,by integrating this global information,the most promising areas will be developed.The success of these methods illustrates the advantages of the multi-subgroup strategy.However,these two improvements do not change the problem that the exploration ability of the algorithm decreases in the later period.At the same time,individuals may still explore better local development areas in the later stage,and the development of local space in the early stage can provide more abundant information for the subsequent optimization.In addition,all subgroups in the multi-subgroup method adopt the same algorithm,which may lead to excessive homogeneity among subgroups,that is,the exploration ability and development ability of each subgroup are very similar.Therefore,the advantages of multi-subgroup strategy cannot be fully exploited.Inspired by the above ideas,this paper proposes a multitopology hierarchical collaborative framework and applies it to MHCHPSO (Multi-Topology Hierarchical Hybrid Particle Swarm Optimization)algorithm.This algorithm balances the diversity and convergence of the algorithm and improves the overall search efficiency of the algorithm.
In this paper,a hierarchical collaborative strategy is proposed based on multi-topological structure,building a multi-topological hierarchical collaborative framework,which includes: diversity topology,fast convergence topology,and collaboration topologies.Diversity topology is used to maintain the diversity of the algorithm.In the whole algorithm running process,all individuals in this topology only consider diversity without considering convergence ability,to solve the problem of premature convergence of PSO.In this paper,Levy flight with random walk capability is used as a diversity topology to provide diversity for the algorithm.The fast convergence topology is used to enhance the convergence ability of the algorithm.During the operation of the algorithm,only the convergence speed of all individuals in the topology is considered,not the diversity.In this paper,a fast local convergence particle swarm optimization is implemented using the Lamarckian mechanism for local development.Since the diversity topology contains a lot of random information,if this information is directly transmitted to the fast convergence topology,it will mislead the fast convergence topology,and then affect the convergence ability of MHCHPSO.Therefore,we design collaboration topology that receive information from diversity topology and provide fast convergence topology with regions where optimal solutions may exist for fast convergence topology development.In other words,the collaboration topology can be regarded as a filter,filtering and processing the information in the diversity topology and providing a high-quality search area for the fast convergence topology.In addition,collaboration topology combines the functions of exploration and development,and maintains a balance between exploration and development.In this paper,two collaboration topologies are designed based on PSO and two adaptive weights are applied,respectively.Two collaboration topologies with different weights have the following two advantages: One is that different search areas can be explored to improve the performance of MHCHPSO.Second,it can contain more heterogeneous search information to avoid the homogeneity of the two collaboration topologies.Finally,the cooperation and information sharing among topologies are realized through the iteration difference analysis strategy(IDAS)and the aggregation estimation strategy(AES)among multiple topologies,and the diversity and convergence of the algorithm are balanced by adaptive algorithm.
The main contributions of this paper are as follows:
• A multi-topology hierarchical collaboration framework is proposed,which includes three types of topologies.Each topology works independently and only interacts with limited information through collaboration topology,so that the algorithm can keep its exploration ability and convergence ability for a long time.
• Memory was added to Levy’s flight,allowing it to record spatial information while exploring space and use it as a diversity topology.A fast local convergence particle swarm optimization is designed based on the idea of “use it or lose it” of the Lamarckian mechanism and is used as a fast convergence topology to provide efficient convergence capability for MHCHPSO.
• Two kinds of adaptive weights are proposed,which are fast convergence adaptive inertia weight with activation and adaptive inertial weight based on intuitionistic fuzzy entropy.These two inertial weights enable collaboration topologies to automatically adjust exploration and development capabilities according to the interactive information from the diversity topology and the fast convergence topology,thus achieving an adaptive balance between algorithm diversity and convergence.
• In this paper,various heuristic algorithms are compared on well-known benchmark function sets,and the problems are compared and analyzed from three aspects: solving accuracy,convergence speed and stability.These experiments verify the competitiveness of the proposed algorithm.In addition,the experiment on WSN location optimization confirms the effectiveness of this algorithm,and provides a new solution for WSN location optimization.
The rest of this paper is set up as follows.Section 2.1 introduces the diversity topology.The collaboration topology is detailed in Section 2.2.The fast convergence topology is explained in Section 2.3.Section 2.4 discusses the information exchange mechanism among topologies.Section III is the experimental part and analyzes the working process of MHCHPSO.Section IV concludes the paper.
II.MHCHPSO
MHCHPSO has three types of topologies: diversity topology,collaboration topology,and fast convergence topology.All individuals are equally divided into four topologies,one of which is diversity topology,one is fast convergence topology,and two are collaboration topology.The MHCHPSO model is shown in Figure 1.
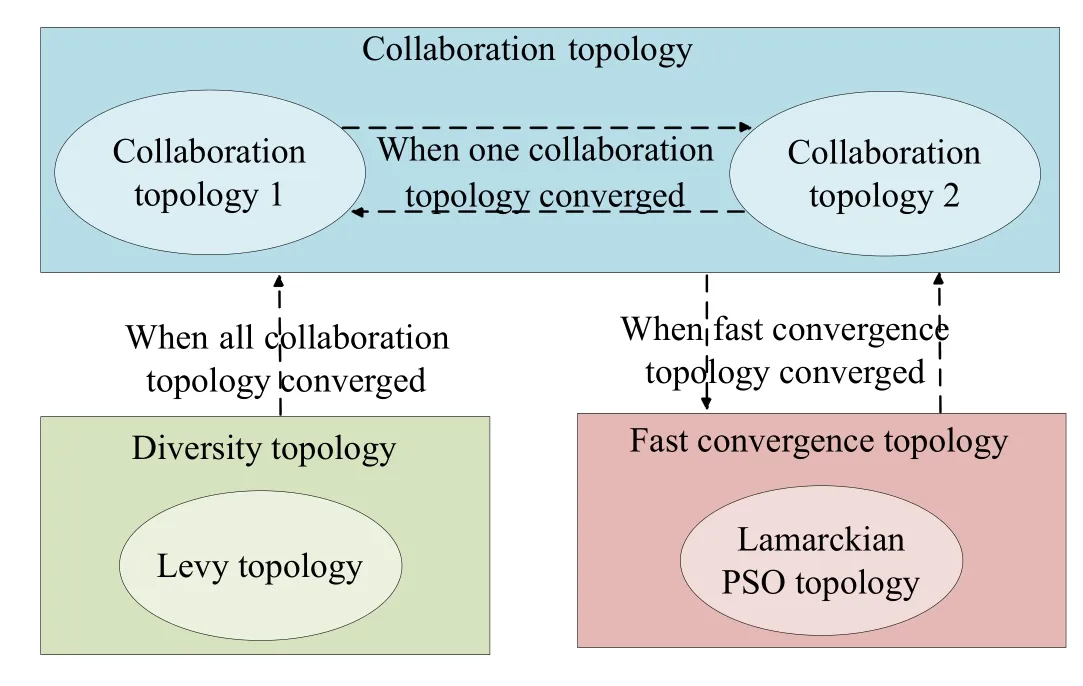
Figure 1.MHCHPSO model diagram.
The diversity topology is used to maintain the diversity of MHCHPSO,which is implemented by Levy Flight in this paper.The fast convergence topology is used for local fast optimization,which is implemented by Lamarck PSO in this paper.Collaboration topology 1 is implemented by a PSO with the adaptive weight proposed in section 2.2.1,and collaboration topology 2 is implemented by a PSO with the adaptive weight proposed in section 2.2.2.As can be seen from the figure,if any collaboration topology converges,information will be exchanged with another collaboration topology.This measure has the following two advantages:First,the search efficiency of each topology can be improved by exchanging search information.The second is that when a topology falls into a local optimal solution,another topology can help it expand its diversity and escape the local optimal solution.Diversity topology will only unilaterally transfer individuals to collaboration topology.This is to prevent the collaboration topology from inputting particles with local information into the diversity topology,which will lead to the loss of the diversity information of the diversity topology.Only when all collaboration topologies converge,the diversity topology will input diversity information to the collaboration topology.This is because the two topologies are likely to fall into the same local optimum when the two topologies converge at the same time.Therefore,diversity topologies are needed to help collaboration topologies escape from local optima.The fast convergence topology interacts with the collaboration topology only when it converges.This is to ensure the continuity of the local optimization of the fast convergence topology.The method to determine whether the topology has converged is described in section“Communication between topologies”.
2.1 Diversity Topology
In the multi-topology hierarchical collaborative framework,the diversity topology is used to maintain the overall diversity of the algorithm,and the ability to maintain the diversity runs through the whole iteration process.In this paper,the random ability of Levy flight is utilized to realize the diversity topology,so the meaning of Levy topology in this paper is equivalent to the diversity topology.Specifically,this paper improves the Levy flight formula of the CS algorithm to improve the ability of Levy flight to maintain the overall diversity of the algorithm.The formula is as follows.
whereαis a random number in range of [0,1],represents the best solution in diversity topology att-1th iterations,represents the historical optimal solution of individualiint-1th iteration.step(β) is the step size of the Levy flight.In this paper,the Mantegna’s algorithm described by Yang[18]is used.
2.2 Collaboration Topology
The collaboration topology plays a central role in the algorithm and maintains the balance between diversity and convergence.When the diversity of the collaboration topology is insufficient,it expands its diversity by interacting with the diversity topology;when the fast convergence topology stagnates,it provides a new local exploitation target for the fast convergence topology.At the same time,the collaboration topology has the works of global exploration and local exploitation.
The collaboration topology in this paper consists of two topologies,each of which has its own best solution.Two topologies realize information interaction by exchanging non-optimal particles in two topologies.This paper implements two collaboration topologies based on Shi’PSO[19],and proposes two adaptive weights as inertial weights of these two collaboration topologies.According to the current population distribution,these adaptive weights will automatically update the weights to achieve the purpose of automatic adjustment exploitation and exploration.
2.2.1 Fast Convergence Adaptive Inertia Weight with Activation
This section proposes a fast convergence inertia weight with activation.When the weight is not activated,the convergence ability is strong,which can prompt the topology to perform a local search.Once particles are introduced from the diversity topology,weights are immediately activated and raised to increase topology diversity.In order to ensure the convergence curve of the topology has a downward trend,the upper bound of the weight is limited by a linearly decreasing function.The formula is as follows.
whererepresents the inertia weight of the collaboration topology 1,trepresents the current number of iterations,the activation pointaprepresents the number of iterations when the most recent interaction occurred,maxIterrepresents the maximum of iterations,a ∈(0,1)is a constant.U1is the upper bound ofb(x),andL1is the maximum decreasing interval ofb(x),andU1>L1.U1andL1reflect the upper limit of the inertia weight and the lower limit of the attenuation degree,this is a decreasing process.
To illustrate the workflow of this adaptive weights,here we draw the corresponding function images forat−apandb(ap),namelyaxandb(x).The functionsaxandb(x) are shown in Figure 2a.The curve represents the functionax,a=0.5,0.8,0.9,0.95 and the line representsb(ap)which is a function that decreases linearly fromU1toU1−L1.HereU1=1toL1=0.8.It can be seen from Figure 2a.that the smaller the weight ofais,the faster the decline speed will be,while the too small weight is likely to cause premature convergence of topology.Therefore,it is more reasonable forato be between 0.8 and 0.95.In this article,a=0.9.

Figure 2.Fast convergence adaptive weight with activation.
Once the collaboration topology 1 interacts with the diversity topology or collaboration topology 2,the inertia weight is activated and setap=t.Therefore,the weight will rise after each interaction and to accommodate the global search of the collaboration topology.However,improper weight increase will interfere with the convergence process to some extent,so functionb(·)is used to control the upper bound.Figure 2b is an example of the weight being activated.In the figure,the horizontal axis represents the number of iterations,the vertical axis represents the inertia weight value,the red curve represents the inertia weight at each iteration,and the blue straight line representsb(x).It can be seen from the figure the collaboration topology is activated at thex1th iteration and thex2th iteration,and the inertia weight rises toy1andy2respectively and then drops rapidly,as shown inap1andap2in the figure.In addition,if the interactions are frequent,wtends to be the inertia weight that linearly decreasing.
2.2.2 Adaptive Inertial Weight Based on Intuitionistic Fuzzy Entropy
Intuitionistic Fuzzy Sets(IFS)[20]is an extension of Zadeh Fuzzy Sets,which has stronger expression and discrimination capabilities than ZFS.Like information entropy,the smaller the intuitionistic fuzzy entropy,the lower the degree of blur and the higher the certainty of the object described by the IFS,and vice versa.Therefore,in order to reflect the convergence state of the topology more effectively,the entropy value is used as a disturbance factor and the inertia weight is dynamically changed with the number of iterations and entropy value change strategy,which has achieved the goal of adaptively balancing the topology’s global exploration capability and local search.We use the intuitionistic fuzzy entropy formula proposed by Wang et al.[21],which formula as follows.
whereµ ∈[0,1],γ ∈[0,1],π ∈[0,1]represents the degree of membership,the degree of non-membership and the degree of hesitation respectively,andµ+γ+π=1.The inertial weight is calculated as follows.The calculation formula is as follows.
whererepresents the inertia weight of the collaboration topology 2 at thetth iteration,ris a random number in range[0,1],andHtis calculated from Eq.(4).U2−L2indicates the proportion ofrin the inertia weight,L2indicates the proportion of the intuitionistic fuzzy entropy in the inertia weight,andU2>L2.Htwill decrease as the population gradually converges.Therefore,U2andL2can be regarded as the upper limit of the inertia weight and the lower limit of the inertia weight attenuation.
At the early stage of iteration,the topology is in the global search stage,and the particles are relatively dispersed and the overall diversity of the topology is high,which result in the degree of particle aggregation is small.In this case,the entropy should be higher to improve the global search capability.At the later stage of iteration,the behavior of all particles tends to stop,and the diversity of the topology is the least,and the degree of particle aggregation is the largest.In this case,the entropy should be low to enhance the local search capability.Through the above analysis,in order to make the intuitionistic fuzzy entropy reflect the correct degree of aggregation of topology,the membership function,non-membership function and hesitation function are designed as follows.
Since the intuitional fuzzy entropy weight does not decrease continuously,the weight will reach its maximum atµt=γt,which can maintain the diversity of the topology.Therefore,compared with the first adaptive weight,the second adaptive weight has slower convergence and stronger global search capability.
2.3 Fast Convergence Topology
The main work of fast convergence topology in the multi-topology hierarchical collaborative framework is to provide fast convergence capabilities for MHCHPSO.Under the guidance of the collaboration topology,the given target region is searched and the optimal solution is fed back to the collaboration topology.This paper uses the Lamarck mechanism to achieve fast convergence topology.
The core idea of Lamarckian theory is“use and disuse”,which means only good species are worth evolving [22].Therefore,this paper applies the characteristics of Lamarckian mechanism to the local search of the algorithm in the following two ways.One is to implement an elite retention mechanism for this topology.Secondly,an evaluation standardη ∈[−4,4] is set for each particle to evaluate the quality of its historical best solution.The largerηis,the better the historical optimal solution is,while the opposite is true.In other words,the particles in the PSO are no longer affected by their own history,but select the history of high-quality particles in the fast convergence topology to learn,and to achieve the purpose of fast local search.
In this paper,for each particle,the league mechanism is used to select the historical optimal solution from other particles according toη.In addition,in order to further improve the convergence speed,the league mechanism is only performed on positiveη.When the number of positiveηis greater than the preset value,it is set to 2 in this paper,and the league mechanism is performed on theηof all particles.It is set to 2 because the league mechanism requires at least two individuals to participate.The formula for calculating theηis as follows.
In Eq.(9),fitrepresents the fitness of the th particle at thetth iteration.In Eq.(10),abs(·) represents the absolute value function,setirepresents the set of particles that select the historical best solution of particleias its own historical best solution.In Eq.(12),rank(A,B) is an ascending sorting function,which represents thatAis sorted first,andBis sorted whenAis equal.numrepresents the number of fast convergence topology particles,which purpose is to normalize the sorted results.The following multiplication by 8 minus 4 is used to scale the normalized result to the interval of [-4,4].Thetanhis a commonly used activation function in machine learning,the formula is as follows,
In addition,because Lamarckian mechanism requires the fitness information of the previous generation of particles,the league mechanism is executed in terms of historical optimal fitness of all particles during the first iteration.If a particle updates its historical optimum,it is always assumed that its historical optimum will be better than before,soη=η+0.1.To sum up,the pseudocode is shown in Algorithm 1.

Finally,the velocity of particles in the fast convergence topology is updated by the following formula.
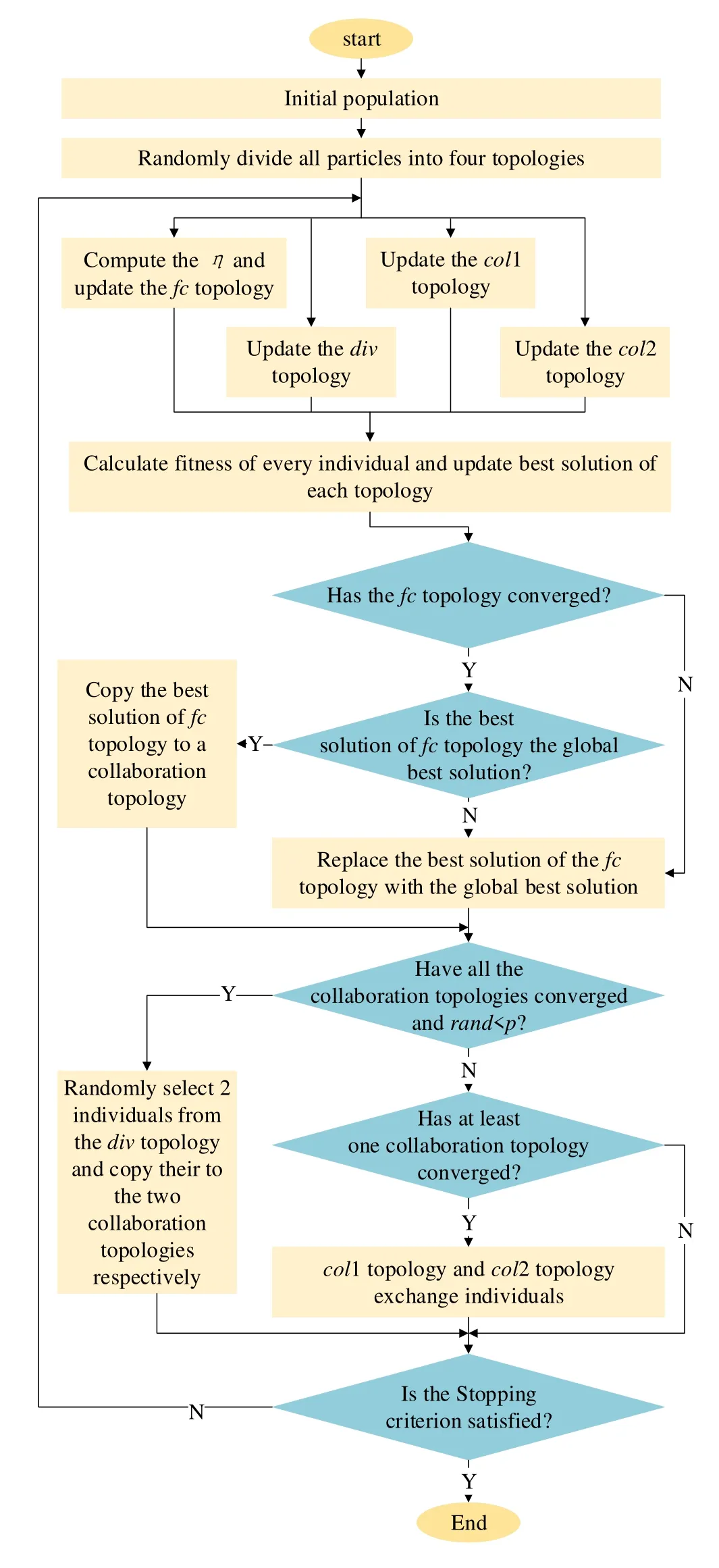
2.4 Communication Between Topologies
In this algorithm,all particles are divided into 4 topologies on average,among which,there are 2 collaboration topologies,1 diversity topology and 1 fast convergence topology.The following rules govern the exchange of information between topologies.
Rule1: When the fast convergence topology converges and its best solution is not global best solution,a particle in the fast convergence topology is randomly replaced with the global best solution.
Rule2: When the fast convergence topology converges and its best solution is global best solution,a particle in the collaboration topology is randomly replaced with the best solution of the fast convergence topology.
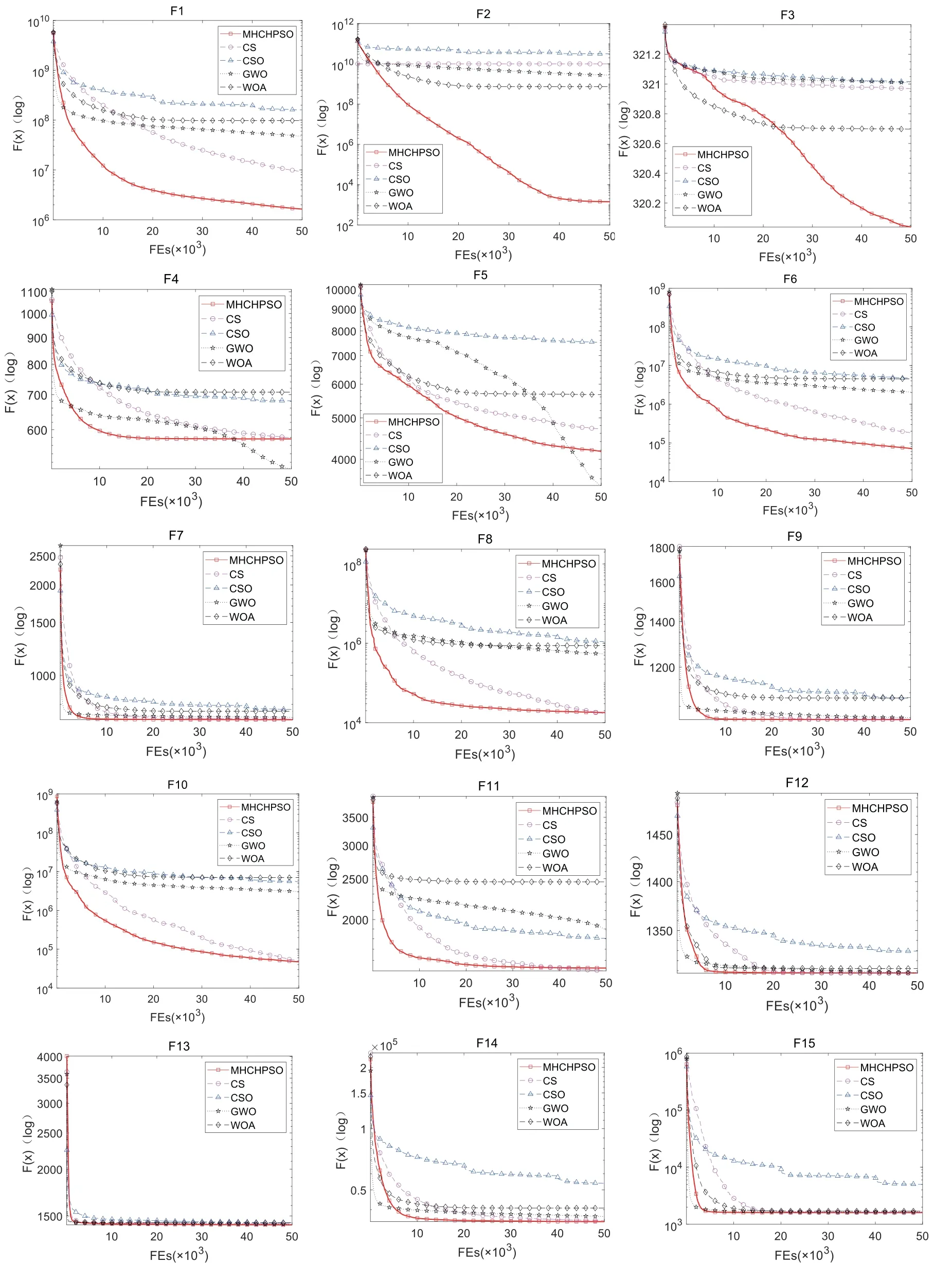
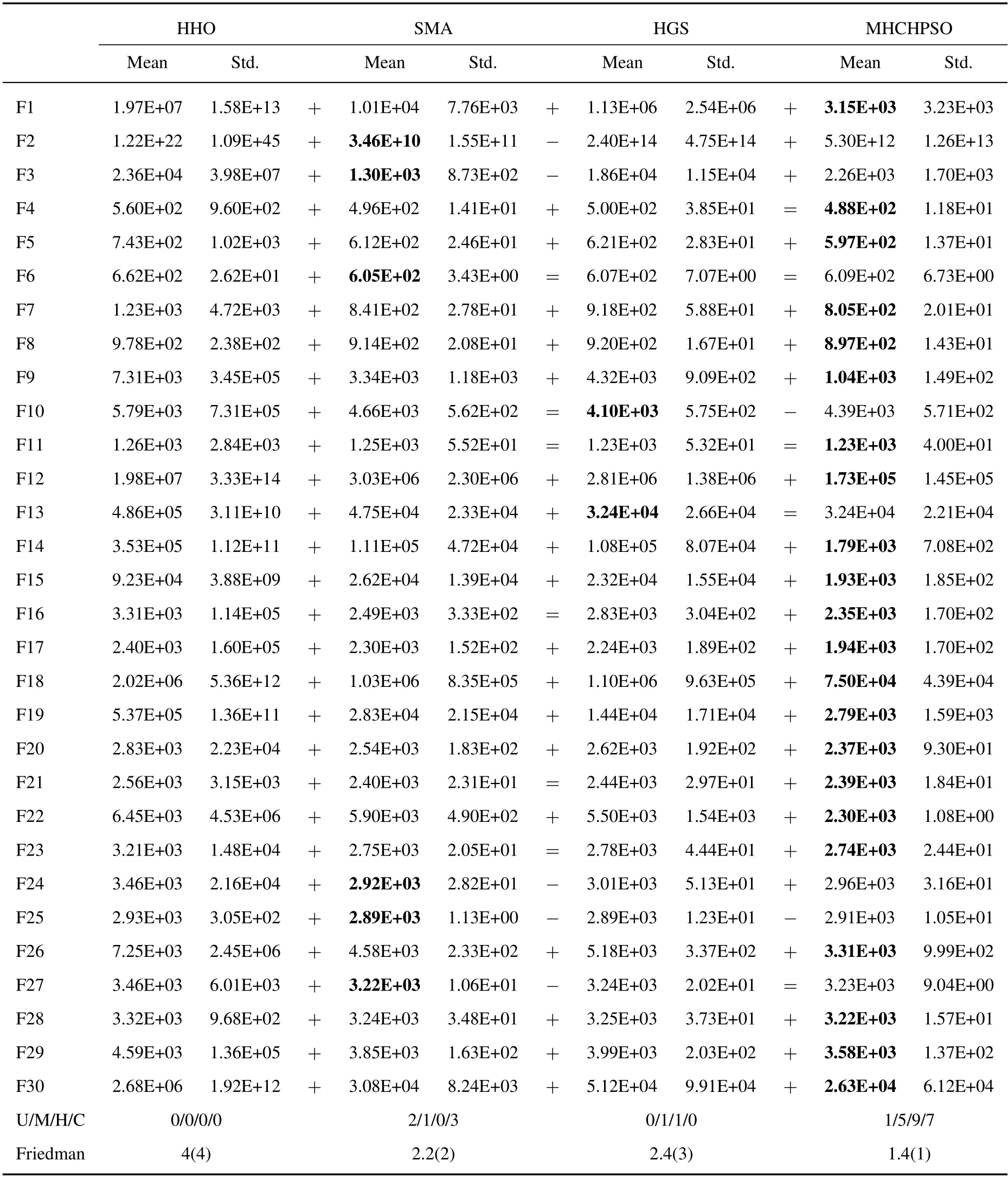
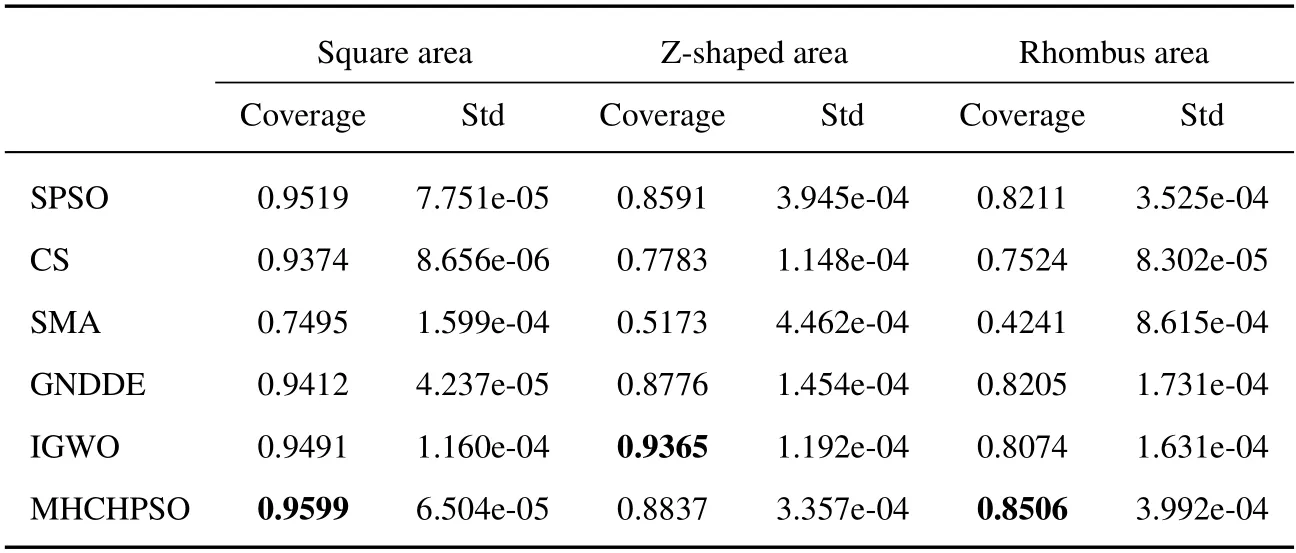
Rule3: When all collaboration topologies converge andrand Rule4: When any collaboration topology converges,the two collaboration topologies randomly exchange a particle. Among the above rules,the purpose of rule 1 and rule 2 is to improve the convergence ability of the algorithm,while the purpose of rule 3 and rule 4 is to maintain the diversity of the algorithm. Because of too frequent implantation of diversity information into the collaboration topology,the collaboration topology cannot enter the local search stage.Therefore,the thresholdpis set.Whenever step 3 is executed,p=0.Each iterationp=p+0.1,untilp=1. In MHCHPSO,there are two kinds of convergence judgment strategies of topology,namely,aggregation estimation strategy (AES) and iteration difference analysis strategy (IDAS).AES and IDAS are used for collaboration topology and fast convergence topology respectively.The AES means that if all the particles in the topology are within the range of[gbestk −neig,gbestk+neig],the topology is considered to have converged,whereneigrepresents the neighborhood size andgbestkis the best solution of collaboration topologykas so far.IDAS means that the optimal particle of the topology does not improve after n iterations,and then the topology is considered to have converged.The reason why the fast convergence topology is used for IDAS instead of AES is that the property of fast convergence topology leads to the fact that the particles will always cluster around the optimal particles.Therefore,AES should not be used in fast convergence topology. According to the above rules,the complete pseudocode of this algorithm is shown in Algorithm 2,and the flow chart is shown in Figure 3. Figure 3.MHCHPSO model diagram. In Figure 3,fctopology represents fast convergence topology,divtopology represents diversity topology,col1 topology andcol2 topology represent collaboration topology 1 and collaboration topology 2 respectively. In order to test the performance of MHCHPSO,this paper compares it with other algorithms on CEC 2013 30D [23],CEC 2015 30D [24],and CEC 2017 30D[25],respectively.The comparison is detailed in the corresponding sections.All experiments were run on matlab2018a of a computer with 64-bit windows 10 system,Intel Core i7-6700 processor and 8 GB of memory.Section 3.2 compares MHCHPSO with various improved PSO algorithms on CEC 2013.In Section Section 3.3,MHCHPSO is compared with the well-known heuristic algorithm at CEC 2015.In Section 3.4,MHCHPSO is compared with heuristic algorithms proposed in recent years at CEC 2017.WSN location optimization experiment is in Section 3.5. In all experiments,MHCHPSO parameters were set as follows.The population sizeN=40.β=1.5 in diversity topology.In fast convergence topology,wlocal=[0.2,0.6],n=10 in CEC 2013 and CEC 2015;in CEC 2017,because the maximum FEs is small,n=5.In collaboration topology,a=0.9,U1=U2=1.2,L1=L2=0.8.The maximum velocity of the individualvmax=,and the minimum velocityvmin=−vmax,neig=,whereubandlbrepresent the upper and lower bounds of the search space respectively.The acceleration coefficient is set asc1=c2=2.Note that maximum velocity,minimum velocity,and acceleration coefficients only apply to fast convergence topology and collaboration topology. In this section,MHCHPSO and various improved PSO algorithms are compared and analyzed on CEC 2013 30D,where F1-F5 is a unimodal function,F6-F20 is a multimodal function,and F21-F28 is a composition function,and the search range is [−100,100]D.The Neighborhood Centroid Opposition-Based Particle Swarm Optimization (NOCOPOS) [26],was selected as comparison algorithm,which has received wide attention in recent years,Meanwhile,we cite its comparison algorithm including PSO,SPSO,OPSO,GOPSO,FIPS,CLPSO.Comparison algorithm parameters and experimental data refer to literature[26].The dimension of the test function was 30,the maximum number of FEs was 100,000,and 25 independent runs.The experimental results are shown in Table 1. Table 1.The comparison results with improved PSO on CEC 2013 30D functions. In Table 1,U/M/C respectively represents the number of optimal solutions for each algorithm on unimodal,multimodal,and composition functions It can be seen from Table 1 that MHCHPSO has the best comprehensive result,with the best result obtained on a total of 11 functions.In other functions,PSO,SPSO,OPSO,GOPSO,FIPS,CLPSO and NCOPSO achieved optimal results on 0,3,3,1,1,4 and 6 functions respectively,among which OPSO and GOPSO were equally optimal on function 26.MHCHPSO achieves 4 best results among 5 unimodal functions.The one reason for this result is that Lamarckian mechanism promotes fast convergence topology to develop local extrema more efficiently.Secondly,at the same time,when the fast convergence topology is stagnating,the collaboration topology can provide it with a better target region,which enables it to restart local search.MHCHPSO achieves 6 best results in multimodal function.This is because the diversity topology provides more diversity for MHCHPSO.When diversity is introduced into the collaboration topology,the collaboration topology can automatically transform from the exploitation stage to the exploration stage through two different adaptive inertia weights,so that MHCHPSO can better search for the global optimal solution in the global scope.On the composition functions F21-F28,SPSO,OPSO and NCOPSO are tied for the first place with two functions,while MHCHPSO is slightly worse than them by one function. The last line in Table 1 is the Friedman test [27].The Friedman test is the average of each algorithm’s ranking on each function,so the smaller the Friedman test,the better the algorithm’s overall performance.It can be seen from Table 1 that the ranking of MHCHPSO is the smallest,so MHCHPSO has a better comprehensive optimization ability than other comparison algorithms. 3.3.1 Accuracy Comparison with Well-known Heuristic Algorithms In order to compare the performance of MHCHPSO,this section compares four well-known heuristic algorithms,including CS [28],CSO [29],GWO [30]and WOA[31]are selected as comparison algorithms in this section and compared in CEC 2015 30D.In CEC 2015,F1-F2 is unimodal function,F3-F9 is multimodal function,F10-F12 is hybrid function,F13-F15 is composition function,and the search space is[−100,100]D.The maximum number of FEs was and 50000,and each algorithm was run independently for 30 times.The parameters of CS,CSO,GWO and WOA follow the original paper.The Wilcoxon rank sum test with significance levelα=0.05 is used in the paper[27].The experimental results are shown in Table 2. Table 2.The comparison results with classical heuristic algorithms on CEC 2015 30D functions. In Table 2,U/M/H/C respectively represents the number of best results for each algorithm on unimodal,multimodal,hybrid,and composition functions.+,−,=respectively indicate that MHCHPSO is superior to,inferior to,and equal to the comparison algorithm in the Wilcoxon rank sum test.It can be seen from Table 2 that MHCHPSO got the best results on 9 functions,while CS,CSO,GWO and WOA got the best results on 2,0,3 and 1 functions,respectively.The above information can prove that MHCHPSO is superior to other algorithms. From Table 2,it can be concluded that MHCHPSO has a huge advantage in unimodal function.This reason is under the guiding ideology of “use and disuse”,fast convergence topology abandons the diversity of the population but improves the local search ability.Therefore,the optimization ability of the algorithm in the local extremum is guaranteed.MHCHPSO also has a big advantage in composition functions.MHCHPSO has the best result for all the composition functions.Because of Levy’s flight characteristics,MHCHPSO can better adapt to complex environments.When the collaboration topology falls into the local optimal,it can introduce diversity from the diversity topology to improve the overall exploration ability of the algorithm.In addition,the fast convergence topology can guarantee the local exploitation ability of the algorithm even if the algorithm is still in the exploration stage.The advantages of MHCHPSO are relatively small,but it is still better than other algorithms On the hybrid function,CS,GWO and MHCHPSO each have a best value. From the Friedman test in Table 2,MHCHPSO ranked first with 1.4667,and was ahead of the secondranked CS by about 1 ranking advantage.This proves that MHCHPSO has better overall performance. 3.3.2 Convergence Analysis In addition to comparing the mean value,this paper analyzes the convergence speed of each algorithm through the convergence curve graph,and analyzes the stability of each algorithm through the box plot.The convergence curve can show the specific situation during the iteration of the algorithm,so the convergence curve can analyze the convergence of the algorithm well.The convergence curve of each algorithm in CEC 2015 are shown in Figure 4. Figure 4.Convergence graph on CEC 2015 30D. It can be seen from Figure 4.that the convergence ability of MHCHPSO is generally better than other algorithms.As for the unimodal function F1-F2,the algorithm can search the best solution faster than other algorithms.This reason is even though MHCHPSO is in the global exploration stage,the fast convergence topology ensures the local convergence ability of the algorithm,and a good solution found by the fast convergence topology can help the collaboration topology to converge better.For multimodal functions F3-F9,MHCHPSO has better optimization ability on F6,F7,and F9.On F5,F6,and F8,the early convergence rate is faster,but the mid-term convergence rate is slower because the fast convergence topology and collaboration topology gradually converge and stagnate.However,when these topologies fall into the local optimum,diversity information is introduced from the diversity topology and adaptive weights are activated so that the collaboration topology alternates between exploration and exploitation.Therefore,although the convergence rate gradually slows down,it effectively avoids falling into local extremums.Although the accuracy of F4 is inferior to the CS algorithm,the convergence speed is faster in the early stage.MHCHPSO reached the result of the CS algorithm 42,000 evaluations in 14,000 evaluations.For the hybrid function F10-F12,MHCHPSO is better than other algorithms on F10 in the whole process.The accuracy on F11 is inferior to the CS algorithm,but the convergence speed is faster in the early stage.The search results of most algorithms on F12 are similar,but MHCHPSO converges faster.MHCHPSO finds the best solution at about 10,000 evaluations,and the CS algorithm with the second convergent speed finds the best solution at 22,000 evaluations.Most algorithms can achieve best solutions on F13 and F15,but MHCHPSO is faster,reaching the best solution after 2000 evaluations and 4000 evaluations,respectively.MHCHPSO is more accurate than other algorithms on F14,and the best solution is found in about 14,000 evaluations,much faster than other algorithms.This reason is MHCHPSO can adapt to complex and variable environments through collaboration topologies and information exchange mechanisms.When the collaboration topology falls into a local extremum,it can escape from the local extremum by interacting with the diversity topology.When the collaboration topology is in the exploration stage,the optimal solution provided by the fast convergence topology can be used to search for regions where the optimal solution may exist. 3.3.3 Stability Analysis In order to compare the stability of the algorithm,boxplot is used as a comparison method.Boxplot is a good analytical tool to evaluate the stability of algorithms.The boxplot takes it into account that the minimum,upper quartile,median,lower quartile,maximum,and outliers of the results of 30 independent runs.Therefore,boxplot can effectively avoid the impact of random errors on algorithm evaluation,and the stability of the algorithm can be intuitively seen.The boxplot on CEC 2015 is shown in Figure 5. Figure 5.Box plot on CEC 2015 30D. Analysis of Figure 5 shows that MHCHPSO not only achieves good results on F1,F2,F6,F7,F8,F9,F10 and F15,but also has high stability.Although the stability of F11,F12 and F13 is slightly lower than other algorithms,the median value is better than other algorithms.The good performance on F1 and F2 proves the effectiveness of the fast convergence topology of MHCHPSO.Fast convergence topology can provide MHCHPSO with better and more detailed local search capabilities.For the multimodal functions F6-F9,it is because the diversity topology can always maintain the diversity of the algorithm,and will not decline with the progress of iteration.Therefore,when the collaboration topology falls into a local extremum,the information exchange mechanism can be used to obtain diversity information from the diversity topology,thereby escaping from the local extremum.For the hybrid function F10-F12,although the stability of MHCHPSO on F11 and F12 is slightly inferior to the second CS algorithm,it has a better median value.This result shows that the CS algorithm is relatively easy to fall into the local optimum,and MHCHPSO has a greater probability of making the algorithm escape from the local extremum.For the composition function F13-F15,the median value of MHCHPSO on F13 is better than other algorithms,and the stability is slightly worse.It is inferior to CS algorithm on F14 but not much different in general.The median value and stability on F15 are better than other algorithms.In general,MHCHPSO performs well and is stable in most algorithms. In addition to comparing with classical heuristics,this paper also compares the recently proposed heuristics,including HHO (2019) [32],SMA (2020) [33],HGS (2021) [34],to measure the competitiveness of MHCHPSO.The selected benchmark function is CEC 2017 30D,in which F1-F3 is unimodal function,F4-F10 is multimodal function,F11-F20 is hybrid function,F21-F30 is composition function,and the search space is[−100,100]D.The maximum number of FEs was 50000,and each algorithm was run independently for 30 times.The parameters of HGS,HHO,and SMA follow the original paper.The experimental results are shown in Table 3. Table 3.The comparison results with recent heuristic algorithms on CEC 2017 30D functions. It can be seen from Table 3 that MHCHPSO has the best performance in 22 functions.HHO,SMA and HGS showed the best performance on 0,6 and 2 functions,respectively.Although MHCHPSO is slightly inferior to SMA on unimodal functions,MHCHPSO outperforms all algorithms on multimodal,hybrid and composition functions.This indicates that MHCHPSO can better adapt to the search environment of complex environment.This is because the diversity topology of MHCHPSO can maintain diversity in a complex environment for a long time,and the collaboration topology can jump out of local extremums with the help of diversity topology.So that MHCHPSO can better search in complex environments.Therefore,in general,MHCHPSO has better performance than the heuristic algorithms proposed in recent years.The Friedman test in Table 3 also verifies this. Wireless sensor network (WSN) is a self-organizing network composed of multiple nodes.In WSN,each sensor has a sensing radius and a communication radius.Each node in WSN can effectively collect data within the sensing radius and transmit data with other nodes within the communication radius.The area within the sensing radius is called the area covered by WSN.Different target areas will be set according to the actual task,and the target area needs to be covered under a given number of sensors.However,the random deployment mode can not reasonably use sensor resources,resulting in low coverage.Therefore,the sensor position needs to be optimized to achieve the highest possible coverage.Since the sensing radius of sensors is usually smaller than the communication radius,WSN coverage optimization can be described as maximizing the coverage within the target area given the number and sensing radius of sensors.To calculate the coverage,a continuous target area is usually divided into a set of square grids,which are considered covered if the center point of the grid is within the sensing radius of any sensor.The formulation is described as follows. wherexjrepresents the position of the sensor,yjrepresents the coordinates of the center point of the grid,rjrepresents the communication radius of sensorj,d(·) represents the distance calculation function,Mrepresents the number of grids,andNrepresents the number of sensors.In order to apply to the optimization algorithm,the objective function is set to 1−Rcov. To test MHCHPSO’s capability on the WSN coverage problem,we chose the top-ranked algorithms in Friedman test other than MHCHPSO from CEC 2013,CEC 2015,and CEC 2017.Therefore,the comparison algorithms selected were SPSO,CS and SMA.In addition,two heuristic optimization algorithms dedicated to WSN coverage optimization were selected as comparison algorithms,namely GNDDE [2] and IGWO[35]. In order to test the performance of the algorithm in detail,and also to meet the needs of special terrain coverage,in addition to testing the regular square area,MHCHPSO’s coverage ability in the Z-shaped and rhombus area was also tested.A square area is a 100m by 100m square area divided into a 100 by 100 grid.The number of sensors is 40,the sensing radius and communication radius are both 10 meters,and the search space is[0,100].Each individual is an 80-dimensional vector representing the 2-dimensional coordinates of 40 sensors.The Z-shaped area is shown as the blue area in Figure 6b,where the number of sensors is 30,the sensing radius is and the communication radius are both 3,and the search space is[0,40].The rhombus area is shown as the blue area in Figure 6c.The number of sensors is 30,the sensing radius and communication radius are both 5,and the search space is [0,80].Each algorithm was run independently 30 times.The experimental results are shown in Table 4. Table 4.Optimized coverage of each algorithm. The results in Table 4 show that MHCHPSO has the best optimization ability and small variance in the square area.This is followed by SPSO,IGWO,GNDDE,CS and SMA.The coverage of MHCHPSO is significantly better than that of the comparison algorithms in both the Z-shaped area and the rhombus area.MHCHPSO coverage ranked second and first in the Zshaped and rhomboid regions,respectively.This indicates that MHCHPSO can better adapt to complex environments and has high coverage.Although MHCHPSO coverage was lower than IGWO in the Z-shaped area,MHCHPSO coverage was better than IGWO in the more complex rhomboid area.This indicates that IGWO performs less well than MHCHPSO in a more complex environment.In conclusion,MHCHPSO can be well applied to a regular deployment environment and can also be used in a complex deployment environment. Figure 6 shows the coverage diagram of each algorithm,which selects the coverage map of the median fitness of each algorithm for 30 runs.The colored circles represent the sensor and its sensing radius,or coverage,while the black dots represent the center of the grid.The blue dots in b)and c)represent special covershapes. In Figures 6a,the SMA has a large gap;the CS has a large overlapping area in the upper right of the image and a large uncovered area in the middle of the image.SPSO has several small gaps in the middle of the image,and the coverage range of edge nodes is beyond the area that needs to be covered.The node in the lower right corner of GNDDE is beyond the target area;the IGWO has a large area of overlap in the lower left corner,while the uncovered area exists in the upper right corner.MHCHPSO had an uncovered area only in the upper right part,and the rest was well covered. In Figures 6b and 6c,since this paper does not strictly restrict the boundary of the search space in the experiment,each algorithm needs to rely on the fitness of the individual to constrain the nodes in the target area.Therefore,it may occur that the sensor node is not in the target area.In Figures 6b,SPSO,CS,and SMA all appear in the case that the sensor nodes are not in the target area,resulting in low coverage of these algorithms.GNDDE has multiple tiny voids.MHCHPSO and IGWO can cover the target area well,and the overlap rate is low.In Figures 6c,all the sensors of MHCHPSO are within the target area,and there is no significant overlap.SPSO,CS,SMA,and IGWO all have sensors outside the target area,resulting in low coverage for these algorithms.Although this is not the case for GNDDE,the overlap of the upper region results in its lower coverage. In conclusion,MHCHPSO neither exceeds the target area nor overlaps a large area in the three deployment environments.Therefore,MHCHCPO is a WSN coverage optimization algorithm with high search accuracy and high stability. This paper proposes a new heuristic algorithm named multi-topology hierarchical collaborative particle swarm optimization (MHCHPSO).In MHCHPSO,three types of topologies are used to overcome the problems of precocious convergence and easy oscillation in local search.In this paper,Levy flight with random walk capability was used as the diversity topology to maintain long-term diversity of MHCHPSO.The fast convergence topology is designed based on the Lamarckism,which makes MHCHPSO have strong local convergence ability.In order to coordinate the diversity topology and fast convergence topology,two collaboration topologies are set up in this paper.In this paper,fast convergent adaptive inertial weights with activation and intuitionistic fuzzy entropy-based inertial weights are proposed for two cooperative topologies. Experimental results at CEC 2013,CEC 2015,and CEC 2017 show that MHCHPSO outperforms the comparative PSO variants,well-known heuristic algorithms,and recently proposed heuristic algorithms,and MHCHPSO has the top Friedman ranking on all benchmarking sets.The analysis of the convergence curve on CEC 2015 proves that the search speed of MHCHPSO is faster than other comparison algorithms.The box plot on CEC 2015 shows the advantages of MHCHPSO in terms of stability.Finally,MHCHPSO is applied to WSN location optimization.Experiments show that MHCHPSO can find the best positioning scheme in complex space without strictly restricting the search space shape.This result shows that MHCHPSO can be easily applied to other complex environments. ACKNOWLEDGEMENT This work was supported by the National Key Research and Development Program Projects of China(No.2018YFC1504705),the National Natural Science Foundation of China (No.61731015),the Major instrument special project of National Natural Science Foundation of China (No.42027806),the Key Research and Development Program of Shaanxi(No.2022GY-331) DATA AVAILABILITY STATEMENTS This paper’s data are all publicly available benchmark sets.The source code for MHCHPSO is available at:https://github.com/VeteranDriverONE/MHCHPSO.
III.EXPERIMENTAL RESULTS
3.1 Experimental Setting
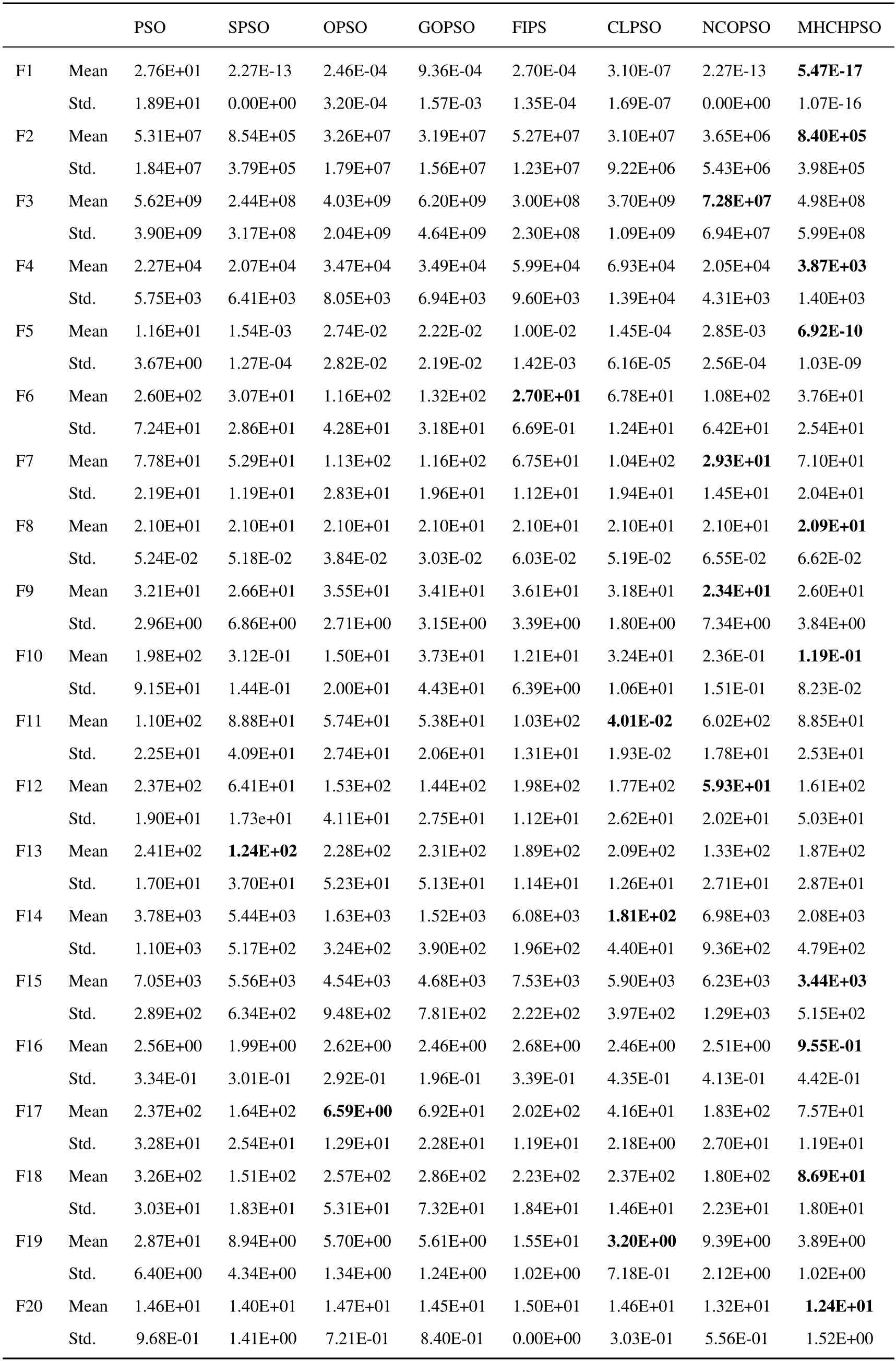
3.2 Accuracy Comparison with Improved PSO on CEC 2013
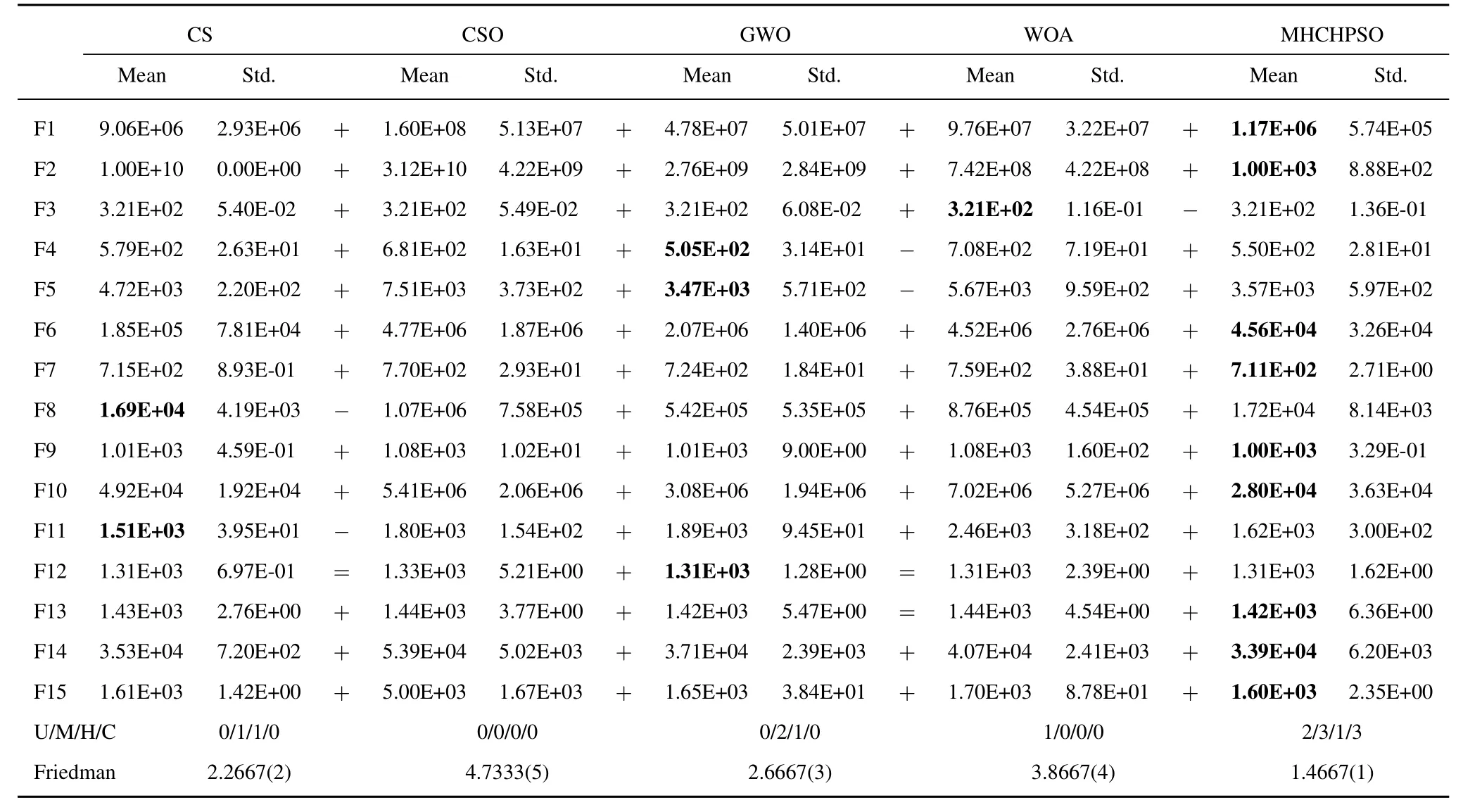
3.3 Comparison with Well-Known Heuristic Algorithms on CEC 2015

3.4 Accuracy Comparison with Recently Heuristic Algorithms on CEC 2017
3.5 Wireless Sensor Network Optimization
IV.CONCLUSION
杂志排行
China Communications的其它文章
- Group-Based Successive Interference Cancellation for Multi-Antenna NOMA System with Error Propagation
- RFID Network Planning Optimization Using aGenetic-Simulated Annealing Combined Algorithm
- Power Allocation and Antenna Selection for Heterogeneous Cellular Networks
- Dielectric Patch Resonator and Antenna
- Discrete Phase Shifts Control and Beam Selection inRIS-Aided MISO System via Deep Reinforcement Learning
- Distributed Edge Cooperation and Data Collection for Digital Twins of Wide-Areas
