Power Allocation and Antenna Selection for Heterogeneous Cellular Networks

Lingyi Kong,Yulong Zou,Yuhan Jiang,Jia Zhu

School of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China

Abstract: In this paper,we investigate the system performance of a heterogeneous cellular network consisting of a macro cell and a small cell,where each cell has one user and one base station with multiple antennas.The macro base station(MBS)and the small base station (SBS) transmit their confidential messages to the macro user(MU)and the small user(SU)over their shared spectrum respectively.To enhance the system sum rate (SSR) of MBS-MU and SBS-SU transmission,we propose joint antenna selection combined with optimal power allocation(JAS-OPA)scheme and independent antenna selection combined with optimal power allocation (IAS-OPA) scheme.The JAS-OPA scheme requires to know the channel state information (CSI) of transmission channels and interference channels,while the IAS-OPA scheme only needs to know the CSI of transmission channels.In addition,we carry out the analysis for conventional round-robin antenna selection combined with optimal power allocation (RR-OPA) as a benchmark scheme.We formulate the SSR maximization problem through the power allocation between MBS and SBS and propose iterative OPA algorithms for JAS-OPA,IAS-OPA and RR-OPA schemes,respectively.The results show that the OPA schemes outperform the equal power allocation in terms of SSR.Moreover,we provide the closed-form expression of the system outage probability(SOP)for IAS scheme and RR scheme,it shows the SOP performance can be significantly improved by our proposed IAS scheme compared with RR scheme.

Keywords: heterogeneous networks;antenna selection;inter-interference;power allocation

I.INTRODUCTION

Due to the overwhelming growth in data traffic generated by the ever-growing number of wireless devices[1,2],there is a growing demand for wide coverage and fast instantaneous transmission rate.However,the traditional cellular networks represented by homogeneous networks [3] only provide basic coverage and limited transmission rate.To this end,heterogeneous cellular networks have been proposed to expand the system coverage and increase the transmission rate at a reduced expense [4–9].The heterogeneous cellular networks usually have a network architecture in which several traditional macro base stations (MBSs) coexist with numerous small base stations(SBSs)[10].By employing dense SBSs into the coverage of MBS,the system capacity and the instantaneous transmission rate of cells can be improved.Moreover,the underlay spectrum sharing (USS) mechanism has been widely used to improve the spectrum efficiency of wireless communication[11].For instance,the authors in[11]jointly improved the energy efficiency and spectrum efficiency by using energy-harvesting and spectrum sharing.However,it also causes mutual interference between different cells,which results in a reduction of the channel capacity[12].

Faced with the increasingly tense status of system resources,multi-antenna technology is an effective approach to enhance the transmission performance of heterogeneous cellular networks without deploying extra terminal equipment such as base stations.As the representation of multi-antenna technology,antenna selection technology [13] has been widely exploited since it does not require strict system synchronization compared with beamforming[14]and space-time coding[15] technologies.Authors of [16] proposed a joint transmit/receive antenna selection scheme with a priority-based genetic algorithm in a multiple-input multiple-output (MIMO) system.In [17],a transmit antenna selection (TAS) was employed to enhance physical layer security in the MIMO wiretap channel with low feedback overhead and low signal processing cost.Moreover,[18] investigated the secrecy outage performance of optimal antenna selection (OAS) and suboptimal antenna selection (SAS)schemes for MIMO underlay cognitive radio systems over Nakagami-m channels.By selecting the optimal antenna at the MBS to maximize the instantaneous transmission rate between MBS and macro user(MU),authors of [4] investigated an opportunistic antenna(OAS)selection mechanism of a heterogeneous cellular network for strengthening physical layer security.

Typically,power allocation schemes can improve the system transmission performance effectively.To be specific,the authors in[19] investigated the tradeoff between secrecy capacity and feedback overhead by employing TAS-Alamouti and power allocation in MIMO wiretap channels.The results indicated that the proposed scheme achieves the better performane than that of conventional TAS [19].Subsequently,the power optimization combined with subcarrier allocation was presented to achieve secrecy transmission for MUs in heterogeneous cellular networks[20].Although TAS and power allocation have attracted much attention from researchers for decades,there are few cases that jointly consider these two technologies in heterogeneous networks.

Inspired by the recent work [4] where the transmit power at MBS and SBS are constant and only TAS was used to increase the system performance,we jointly consider TAS scheme and optimal power allocation for the heterogeneous cellular networks to further improve the system performance in terms of system sum rate(SSR)and system outage probability(SOP).

Our main contributions are summarized as follows.

• We present joint antenna selection combined with optimal power allocation (JAS-OPA) and independent antenna selection combined with optimal power allocation(IAS-OPA)schemes to enhance the reliability for a two-tier heterogeneous cellular network where a macro cell coexists with a small cell,each cell has a user and a base station which is equipped with multiple antennas.The difference between JAS-OPA and IAS-OPA is that the interference channel coefficient is available or unavailable for MBS and SBS.To elaborate,the antenna selection and OPA are jointly considered to maximize the SSR in the JAS-OPA scheme.On the contrary,the IAS-OPA scheme separately employs the antenna selection and OPA to enhance the SSR.Moreover,the roundrobin(RR)antenna selection combined with OPA is also considered as a benchmark which is named RR-OPA.The instantaneous channel state information (CSI) of all channels is assumed to be available.In principle,the CSI can be estimated at the receiver with the transmission of training sequences while it is available for the transmitter by a feedback channel [21,22].For simplicity,we only consider the perfect CSI can be estimated throughout this paper.

• This power optimization problem is non-convex.As a result,we first resort the D.C.approximation method [23] to transform the non-convex problem to an approximately convex optimization problem.In order to illustrate the advantage of our proposed schemes,we also analyze the equal power allocation (EPA) combined with antenna selection as benchmark schemes.Correspondingly,the antenna selection schemes with EPA are named as JAS-EPA,IAS-EPA and RR-EPA,respectively.The numerical results show that our proposed OPA schemes perform better than EPA schemes in terms of SSR and SOP.Moreover,JAS-OPA achieves the best performance among these schemes.

• We provide the closed-form expressions of SOPs for IAS and RR schemes.The numerical results are consistent with our closed-form expressions.It is indicated that the SOP performance of IAS scheme performs better than that of RR scheme.Moreover,an improving SNR will make the performance gap between IAS and RR become large.Furthermore,as SNR increases beyond a certain value,both the schemes converge to their SOP floors,where IAS has the lower floor than RR.

The rest of this paper is organized as follows.We describe the system model in Section II.Next,in Section III,we propose JAS-OPA,IAS-OPA and RR-OPA schemes and present the corresponding iterative algorithms and give the solutions to solve the power allocation problems.In Section IV,the SOP analysis of IAS and RR schemes relying on EPA and OPA methods is carried out and provide the closed-form expressions.Finally,Section V concludes this paper.

II.SYSTEM MODEL

In this section,we first describe the system model of a two-tier heterogeneous cellular network consisting of a macro cell and a small cell.As shown in Figure 1,the small cell is employed in the region of the macro cell.The macro base station(MBS)and the small base station(SBS)are connected to a mobile switch center(MSC)through fibers.For notational convenience,the transmit power of MBS and SBS is denoted byPMandPS.Meanwhile,Q={Ai|i=1,2,···,N}represents the set ofNantennas at MBS whereas the set ofMantennas at SBS is denoted byR={Bj|j=1,2,···,M}.Although,we assume MU and SU are equipped with only one antenna.Following the previous works[24,25]and[17,26],the similar results in single-input multiple-output [24,25] can be obtained in multiple-input multiple-output [17,26].As a result,the similar outcomes in this paper can be readily extended to the scenario that the user equipped with multiple antennas.

Figure 1.A two-tier heterogeneous cellular network consisting of a macro cell and a small cell.

We select the antennaAiandBjfrom the setQand setRaccording to antenna selection criteria,then the selected antennas access to the allocated frequency band and send messages to corresponding users.With the help of the underlay spectrum sharing mechanism(USS),MBS and SBS transmit their respective confidential messagesxMandxSover the same spectrum band simultaneously.We define theAi-MU,Bj-SU channels as transmission channels.As pointed out in [27] that if the distribution of small base stations within the coverage of the macro base station is sparse,the external interference received by users inside the small cell mainly comes from the macro cell,which means the interference caused by users in the same cell could be ignored.Thus,we only consider the interference from the different cells throughout this paper.In this case,we define the wireless linksAi-SU andBj-MU as interference channels.

wheren0is the AWGN that encountered at MU and SU.

The instantaneous transmission rate of the macro cell and small cell are denoted byRmandRs.With the help of Shannon formula and Eq.(1),the transmission rate ofAi-MU channel in the macro cell can be directly obtained as

Similarly,the instantaneous transmission rate ofBj-SU transmission channel can be obtained from Eq.(2)

III.ANTENNA SELECTION AND POWER ALLOCATION FOR SSR OPTIMIZATION

In this section,we propose JAS and IAS schemes to improve the system performance in terms of the system sum rate (SSR).And round-robin (RR) antenna selection scheme is also regarded as a baseline.Due to the existence of mutual interference,antennaAi(Bj)not only transmits signal from MBS(SBS)to the corresponding user MU(SU)but also cause the interference signal at SU(MU)in the small(macro)cell through the interference channel.Additionally,the OPA mechanism is also employed to optimize the SSR.The power allocation factorαij(0≤αij ≤1)is defined as the ratio of the MBS transmit powerPMto the total transmit powerPprovided that the antennaAiof MBS and the antennaBjof SBS are selected to transmit data information to their corresponding users.HencePM=αijP,PS=(1−αij)P.For the given system in Figure 1,the SSRRijis defined as the sum of the macro cell transmission rateRmand the small cell transmission rateRsand is shown in

whereγ=represents the signal-to-noise ratio(SNR),γM=αijγandγS=(1−αij)γ.

Each antenna pairAiandBjcorresponds to an optimal power allocation factorαijand it can be calculated through the D.C.approach in the following chapter.Without loss of generality,we assume the optimal antenna pair isAandBand the corresponding optimal power allocation factor is represented asα∗.In this way,Eq.(5)can be rewritten as

wherehAmandhBmrespectively denote the channel gain from the best antennaAof MBS to MU and the interference channel gain from the best antenna of SBS to MU.Additionally,hBsandhAsseparately represent the wireless channel gains of SBS-SU and MBS-SU.

In the following subsections,we will show how to solve the power optimal allocation.Moreover,when the equal power allocation(EPA)is applied to the system,αij=0.5.The instantaneous CSI ofAi-MU.Ai-SU,Bj-SU andBj-MU channels are assumed to be available at MU and SU through channel estimation and channel feedback.For the convenience of calculation,the imperfect CSI caused by channel estimation error and time delay is not considered in this paper.

3.1 JAS-OPA Scheme for SSR Optimization

In this subsection,the instantaneous CSI of transmission channels(Ai-MU,Bj-SU)and interference channels (Ai-SU,Bj-MU) are jointly considered through the antenna selecting process.The corresponding SSR ofAiandBjfor the whole system is shown in Eq.(5),where|hAim|2,|hBjs|2,|hAis|2|hBjm|2andγare fixed values.First of all,we need to find the optimal power allocation factorαij.The optimization problem of the SSR relying on JAS-OPA scheme is given by

Meanwhile there is an optimization problem to be solved,which is showns as problem(8).

Therefore,the JAS-OPA criterion in this subsection can be expressed as

With the help of antennaA,Bandα∗,the optimization SSR can be obtained in Eq.(6).

Lemma 1.The objective function of optimization problem(8)is non-convex.Proof.Please see Appendix.

The following pages show the calculation ofαij.Since the approximateg2(αij) can be changed into a linear function with the help of D.C.approximation method,we create a feasible solutiong2()ofg2(αij).According to the first-order of Taylor series expansion ofg2(αij),we can obtain Eq.(11).Combining the problem (8) and Eq.(11),an approximate optimization problem is given by problem(12).

The optimal solution to Eq.(12) at iterationkandk+1 are assumed as (k) and (k+1).Through the iterative procedure Eq.(13)we use an optimal power allocation algorithm to solve Eq.(12).

Algorithm 1 shows an iterative power allocation algorithm to achieve optimal solution of our formulated JAS-OPA problem in Eq.(12).We can obtain the optimal power allocation solutionαk+1through problem(8)based on the givenαk.Unless all the updated datas nearly keep unchanged,shown as|gk+1(α)−gk(α)| ≤ζ,or the number of iterations approach to the maximum valuekmax,iterate step stops.

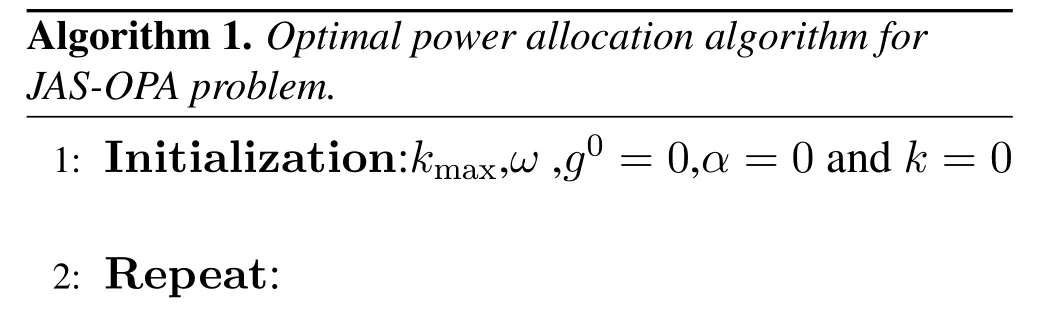
Then we use the solutionαijto calculateRijin Eq.(10).DenotingUas the set of allαij.After that,through the selection criterion Eq.(9),we can obtain the best antennaA,Band the corresponding factorα∗.

Convergence proof of the iterative process is shown in the following pages.From Eq.(11),we can obtain Eq.(14).

Following the iterative procedure in Eq.(13)we can achieve Eq.(15).

Thus,using Eq.(14) and Eq.(15),we can further achieve Eq.(16).

3.2 IAS-OPA Scheme for SSR Optimization

Differ from the JAS scheme,the antenna selection criterion of IAS scheme works on the assumption that only the CSI of transmission channels is known to MU and SU by channel estimation[21].Since the interference from the other cell is unavailable in some scenarios,the optimal antennaAwhich maximizes the transmit rate of the MBS-MU channel will be selected according to the instantaneous CSI of MBS-MU.With the same principle,the optimal antennaBcan be selected to maximize the capacity of SBS-SU.Thus,the selection criterion of IAS is obtained as Eq.(17):

Subsequently,we use OPA to further improve the existing transmission performance.The SSR optimization problem can be written as

In this subsection,we have already selected the optimal antennasAandBaccording to the selection criterion of IAS in Eq.(17),their corresponding optimal power allocation factor can be obtained through the procedure which is the same as JAS scheme.After that,the maximum SSR can be obtained.

It should be noted that in order to obtain the optimal antenna in each time slot,JAS jointly requires antenna selection in macro cell and small cell to maximize the SSR.On the contrary,the IAS scheme just independently selects transmit antenna in macro cell and small cell.Consequently,the computational complexity of IAS is obviously lower than that of JAS under the same circumstances.

3.3 RR-OPA Scheme for SSR Optimization

Without using any antenna selection method,the RR scheme is treated as a benchmark.We select one antenna from the setQand one from setRfor transmission in each time slot.Each antenna has the same probability of being chosen.Therefore,there areNMantenna pairs in each time plot.AiandBjhave a corresponding SSRRij.Hence,the maximum SSRRin this subsection is given by the average value of allRij,which is shown in Eq.(19).

OPA scheme can be carried out directly when we applied the RR scheme to the system.In this case,the optimization problem is shown as Eq.(20).

The solving process of the optimal power allocation factorand the convergence proof are the same as that of the JAS-OPA scheme which is shown as before.Hence,the maximum SSR can be calculated by Eq.(21).

Although the optimization problems and the process of obtaining the optimal power allocation factorα∗of RR-OPA and JAS-OPA are the same,JAS-OPA selects the maximum SSR and returns the best performance antennasA,Band the corresponding optimal allocation factorα∗.However,RR-OPA only performs the ergodic operation without choosing the best performance antennas.As a result,the computational complexity of RR-OPA is the lowest among these schemes and the JAS-OPA requires the most computational resource.Table 1 details the computational complexity for JAS-OPA and IAS-OPA as well as RR-OPA schemes.Wherein,

Table 1.The computational complexity for JAS-OPA,IASOPA and RR-OPA.

3.4 Numerical Results

In this subsection,we analyze the system performance in terms of the SSR versus SNRγof JAS,IAS and RR schemes.The system performance is also optimized by OPA.The average channel gains have the value that=0.1,unless otherwise stated.The power allocation factorαis set toα=0.5 when the EPA method is applied to the system.

Figure 2 illustrates the simulated SSR versus SNRγof the JAS,IAS and RR schemes.We use Eq.(6),Eq.(9)and Eq.(10)to obtain the SSR of JAS through Monte-Carlo simulations.Eq.(6) and Eq.(17) are used to obtain the simulated SSR of IAS while the SSR of RR scheme is simulated by Eq.(19) and Eq.(21).With an increasing SNR,the SSR of three schemes increase first,then converge to their respective outage floors at high SNR region.JAS achieves the highest convergence value compares with IAS and RR schemes.What’s more,Figure 2 depicts that the JAS scheme brings the most elevated performance benefits to the system than IAS and RR schemes in the same situation,which verifies the proposed scheme significantly optimizes the system performance in terms of SSR.

Figure 2.SSR versus SNR (γ) of the JAS,IAS and RR scheduling with EPA scheme.

In order to verify the convergence behavior of the proposed OPA algorithms,Figure 3 shows the converge behavior of JAS-OPA.IAS-OPA and RR-OPA versus the number of iterations withγ=20dB.Simulation results illustrate that the SSR of three schemes converge to system rate floors,verifying that the proposed Algorithm 1 has good convergence performance.

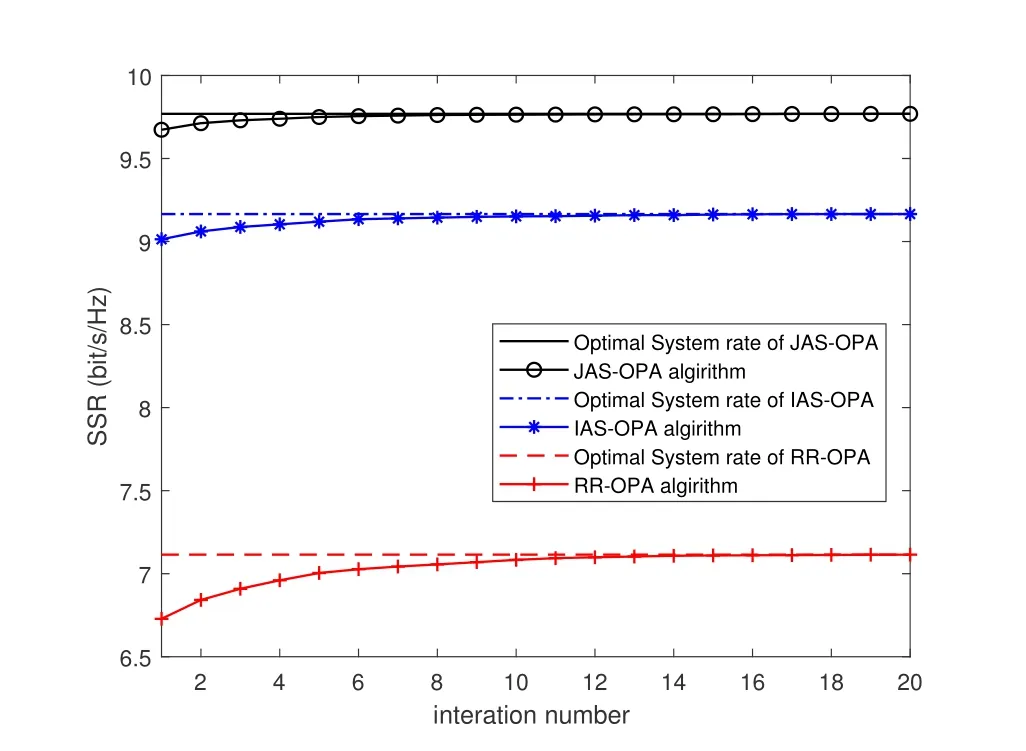
Figure 3.Convergence behavior of the proposed OPA algorithms for JAS,IAS and RR schemes versus the number of iterations with SNR=20 dB.

Moreover,we present numerical simulation results of the SSR for JAS-OPA,IAS-OPA and RR-OPA.JAS-EPA,IAS-EPA and RR-EPA are regarded as benchmarks.It can be seen from Figure 4 that with the help of OPA,the system performance is greatly improved compared with that of EPA in terms of the SSR,especially in the high SNR region.Take the JAS scheme as an example,as the value of SNR reaches up to 25dB or more,the JAS-OPA scheme’s system rate continues to increase while the JAS-EPA scheme converges to a system rate floor since it allocates equal power to two base stations.IAS and RR schemes have this tendency,too.Moreover,we can see that the difference between JAS-OPA and IAS-OPA is not very obvious,which shows that the OPA scheme has more influence on the SSR than AS schemes in this paper.

Figure 4.SSR versus SNR γ of JAS-OPA,IAS-OPA,RROPA,JAS-EPA,IAS-EPA and RR-EPA schemes.

IV.ANTENNA SELECTION AND POWER ALLOCATION FOR SOP OPTIMIZATION

In this section,we derive the closed-form expressions of the system outage probability(SOP)for IAS and RR schemes to characterize the system reliability.OPA is also used to further improve the system performance.

With the assumption that the perfect instantaneous CSI of all channels is available during the antenna selection process,there areNMpossible antenna pairs to be selected for the proposed JAS scheme.Through the simulation results,it is obvious that the system performance of the JAS-OPA and IAS-OPA is almost the same in terms of the SSR,while the IAS scheme only requires the instantaneous CSI of transmit channels.Since the accuracy of channel estimation and feedback delay may have a great influence on CSI[28,29],the JAS does not apply to the system which is challenging to obtain all the instantaneous CSI.However,IAS overcomes the JAS’s shortcoming of the strict requirement for CSI,meanwhile it can obtain near optimal performance as JAS scheme with less computational resource compared with JAS scheme.Hence,we focus on IAS to analyze the system performance.As we mentioned before,the instantaneous transmission rates of both the macro cell and small cell through simulation are available with all the instantaneous CSI.In the following parts,we will analyze the system reliability in terms of system outage probability with the IAS scheme.RR is still the benchmark scheme.Meanwhile,OPA is also be used to further improve the system performance.

In this section,RmandRsstill represent the instantaneous transmission rate of the macro cell and small cell whileR1andR2are their corresponding predefined threshold rate.Outage events will occur when the transmission rate is less than the predefined rate.Thus,are the outage probabilities of macro cell and small cell and can be written as in Eq.(23) and Eq.(24),respectively.When the macro cell and small cell are all succeeded in transmitting data to their corresponding users,there will be no outage events occurred in the system.

The successful transmission probability of the system is the product of the probability of both cells’s successful transmission.Therefore,we can define the SOP for the whole system as

In this section the OPA method is applied to the system.We are going to analyze the system performance for IAS-OPA and RR-OPA schemes in terms of SOP.

4.1 IAS-OPA Scheme for SOP Optimization

In order to minimize the SOP,the selection criterion of IAS is obtained as

According to Eq.(25),the problem of minimizing the SOPPoutis equal to maximizing the system capacities for macro cell and small cell.In this way,we need to maximize the channel transmission rateRMandRS.Thus the selection criterion of IAS can still be written as Eq.(17).

Eq.(27)can be rewritten as Eq.(28),where|Q|and|R|represent the number of antenna sets,whileQ(k)represents thek-th non empty subset of the antenna setQ,R(l)represents thel-th non empty subset of setR.Let us denote Pout=p(αij),the optimal problems based on IAS-OPA scheme can be expressed as Eq.(29)and Eq.(30),respectively.

When the SNR is a fixed value,αijis the only variable in Eq.(29).Solve the equationp′(−αij)=0,if the solutionα∗exists in the interval[0,1],comparing the value ofp(α∗),p(0),p(1).Ifp(α∗)is the smallest among three value,thenα∗is the optimal power allocation factor corresponds to the optimal antenna pairAandB.

The example in Figure 5 illustrates that there exits a minimum SOP of the proposed IAS-OPA scheme when SNRγ=15dB.The trends of the curves are the same according to the different values of SNR.

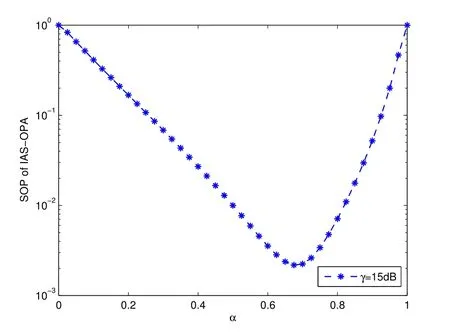
Figure 5.SSR versus α of OPA-IAS with SNR γ=15 dB.

Moreover,Table 2 shows the optimal power allocation factors calculated according to Eq.(29).For convenience,the value ofα∗is accurate to four decimal places.It can be seen from the table that with the help of OPA,the power allocation between base stations is optimized.Moreover,when theγreached up to 25dB,the OPA factorα∗does not change.

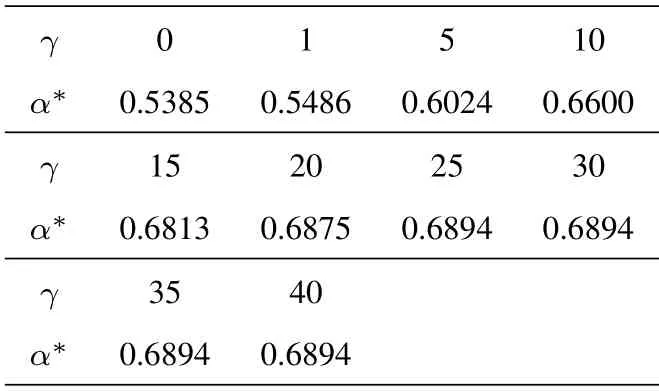
Table 2.Optimal power allocation factor α∗versus SNR γ(dB)of IAS-OPA scheme.

4.2 RR-OPA Scheme for SOP Optimization

In this subsection,we analyze the SOP performance for RR scheme where each antenna has an equal probability to transmit the data to users.Thus,the SOP of RR can be written as

For the EPA,the power allocation factorαisα=0.5 for each antenna selection scheme.The following section will analyze the searching process of the optimal power allocation factor relying on OPA.The optimization problem of RR-OPA can be written as Eq.(33)

In this case we only need to calculate the optimal power allocation factorαfor the antennaAiandBj.Similar to the IAS-OPA scheme,the optimal power allocation factor of RR-OPA corresponding to different SNR(γ) can be obtained in Table 3.To make the results more obvious,the number is correct to eight decimal places.

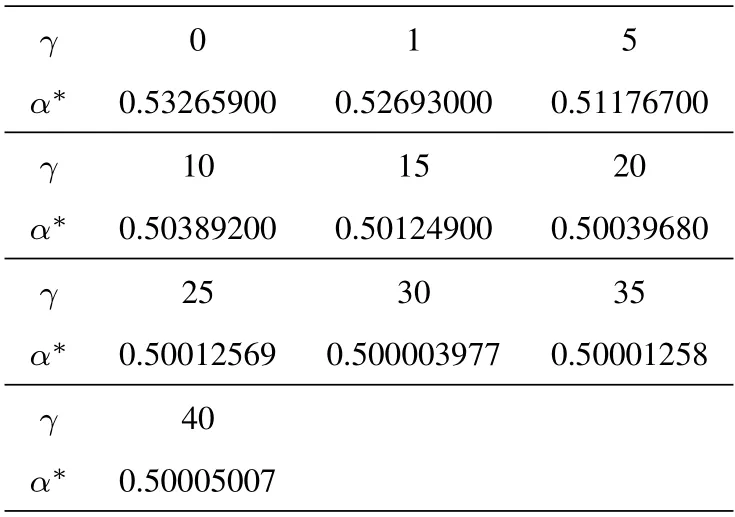
Table 3.Optimal power allocation factor α∗versus SNR γ(dB)of RR-OPA scheme.

After calculating the OPA factors of all antenna pairs,bring them into Eq.(32) to get the minimum SOP.Table 3 shows that the OPA scheme has no obvious effect on the RR scheme since there is no need for antenna selection,when the SNR reaches up to 25dB,the OPA factorα∗is the almost the same as EPA factorα,whereα=0.5.

4.3 Numerical Results

In this subsection the numerical simulation of IASEPA,RR-EPA,IAS-OPA and RR-OPA schemes is shown as follows.To highlight the difference between the two cells,since the small cell may be deployed in a shadowed area of the macro cell and the distance between SBS and SU is shorter than MBS to MU,the average channel gains are given as=1,=1,=0.1 and=0.5.Additionally,the number of antennasN=4,M=4,RM=RS=0.5 bit/s/Hz are assumed.Eq.(27)and Eq.(31)can be simulated by Monte Carlo simulation.

Figure 6 illustrates the SOP versus SNRγfor the proposed IAS and RR schemes with EPA and OPA.We first verify the derived closed-form expressions in Eq.(27) and Eq.(28).When the transmit power is equally allocated to MBS and SBS,the curve drawn by the instantaneous CSI according to Eq.(27)relying on the IAS-EPA scheme matches precisely with the curve drawn by the statistical CSI through the Monte Carlo simulations according to formula Eq.(28).Similarly,with the help of the RR-EPA scheme,it is found that the analytical curve of Eq.(32)coincides with the curve drawn by the simulation result Eq.(31).Therefore,the correctness of the closed-form expressions is verified as we expected.

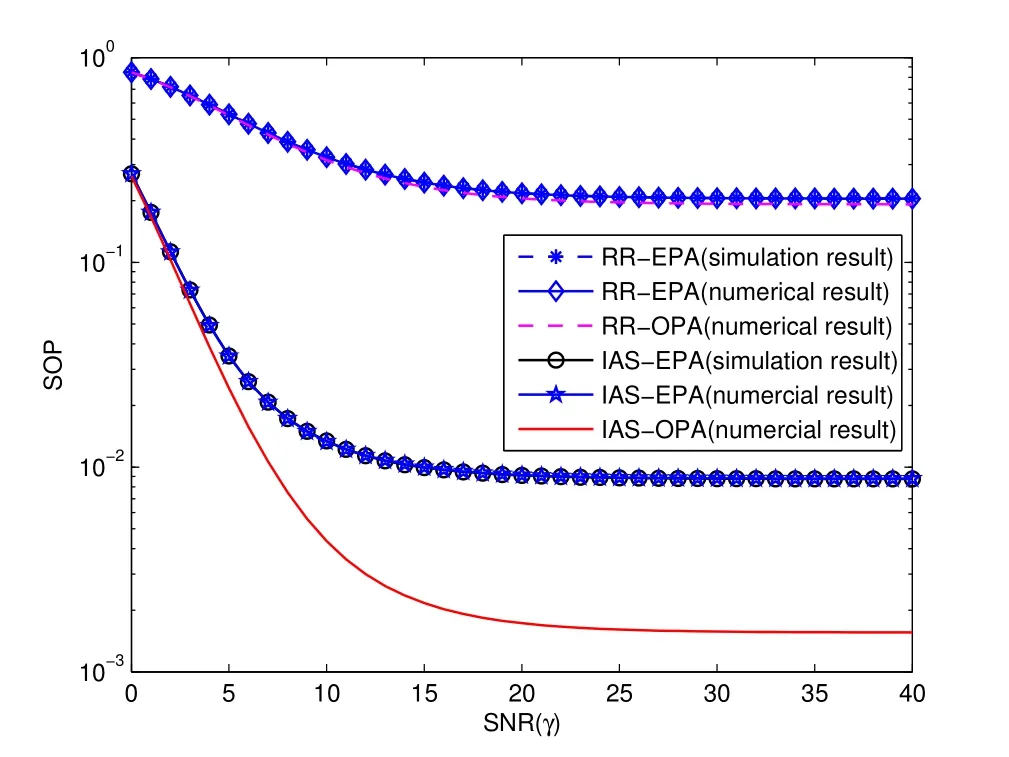
Figure 6.SOP versus SNR(γ) of IAS-EPA,IAS-OPA,RREPA and RR-OPA.

Moreover,Figure 6 demonstrates that no matter using IAS or RR scheme,OPA achieves lower SOP than EPA.Hence the system reliability is significantly increased by OPA.Obviously,the SOP of IAS outperforms RR no matter the adoption of OPA and EPA methods.This can be explained that the RR scheme allows each antenna have equal chance to transmit the private message to user,therefore,the total SOP of RR scheme is the average of all antennas.While IAS scheme employs best antenna to maximizein macro cell andin small cell thereby maximizing the channel capacity for MBS to MU and SBS to SU.In this way,the performance of IAS scheme is significantly increased compared with RR scheme.Additionally,the SOP performance of OPA scheme outperforms EPA scheme,which further results in an improvement of SOP performance for IAS-OPA and RR-OPA schemes.What’s more,limited by the characteristics of the selection mechanism,the variation ranges of SOP of IAS-OPA and RR-OPA are different.The SOP of IAS-OPA has declined rapidly as shown in Figure 6,whereas the SOP of RR-OPA hardly changed.This is due to the fact that without the antenna selection process,no improvement is obtained for a sufficiently high level of SNR which is related to the total transmit power.Since Table 3 reflects that the difference between the OPA factors of the RR-OPA scheme and EPA factors of RR-EPA is small,The variation of SOP between RR-EPA and RR-OPA is not as obvious as that of the IAS-EPA and IAS-OPA scheme.On the contrary,the proposed IAS-OPA scheme outperforms the IAS-EPA scheme in terms of SOP,since the proposed scheme jointly considers the antenna selection and power allocation schemes.

V.CONCLUSION

In this paper,we investigated the transmission performance of a heterogeneous network consisting of a macro cell and a small cell where each cell was composed of one user and one base station with multiple antennas.To maximize the SSR,the JAS and IAS schemes were proposed to jointly select the transmit antennas of MBS and SBS.The RR scheme was also presented as benchmarks.Then we formulated the SSR maximization problems through OPA between MBS and SBS and proposed iterative OPA algorithms to address the optimization problems.Simulation results illustrated that the performance of the proposed JAS scheme outperforms the IAS and RR schemes.Interestingly,with the help of the OPA,the IAS-OPA and JAS-OPA schemes could achieve almost the same SSR,especially in high SNR region.In addition,we derived the closed-form expressions of the SOP for the IAS and RR schemes and verified by simulation and the SOP of IAS is lower than that of RR illustrating the advantage of our proposed IAS scheme.

ACKNOWLEDGEMENT

This work was supported by National Natural Science Foundation of China (No.62071253) and Postgraduate Research and Practice Innovation Program of Jiangsu Province(KYCX21_0747).

APPENDIX

Here we give the proof of lemma.In the following equations,a1,a2,b1,b2,c1,c2are constants whilexis a nonnegative variable (0≤x ≤1).The objective functions in Eq.(16)is positive linear combination of logarithm functions

The concavity and convexity of the function relies on concave-convex characteristic of its restriction to any line.For this reason we can achieve the first and second order derivatives.

It it clear that the positive and negative characterizes ofdepends on specific value ofa1,a2,b1,b2,c1,c2andx,which meansh(x)is non-convex.