Distributed Edge Cooperation and Data Collection for Digital Twins of Wide-Areas
2023-08-26MancongKangXiLiHongJiHeliZhang
Mancong Kang,Xi Li,Hong Ji,Heli Zhang
Key Laboratory of Universal Wireless Communications,Beijing University of Posts and Telecommunications,Beijing 100876,China
Abstract: Digital twins for wide-areas(DT-WA)can model and predict the physical world with high fidelity by incorporating an artificial intelligence (AI)model.However,the AI model requires an energy-consuming updating process to keep pace with the dynamic environment,where studies are still in infancy.To reduce the updating energy,this paper proposes a distributed edge cooperation and data collection scheme.The AI model is partitioned into multiple sub-models deployed on different edge servers(ESs)co-located with access points across wide-area,to update distributively using local sensor data.To reduce the updating energy,ESs can choose to become either updating helpers or recipients of their neighboring ESs,based on sensor quantities and basic updating convergencies.Helpers would share their updated sub-model parameters with neighboring recipients,so as to reduce the latter updating workload.To minimize system energy under updating convergency and latency constraints,we further propose an algorithm to let ESs distributively optimize their cooperation identities,collect sensor data,and allocate wireless and computing resources.It comprises several constraint-release approaches,where two child optimization problems are solved,and designs a largescale multi-agent deep reinforcement learning algorithm.Simulation shows that the proposed scheme can efficiently reduce updating energy compared with the baselines.
Keywords: digital twin;smart city;multi-agent deep reinforcement learning;resource allocation
I.INTRODUCTION
Digital twin (DT) is a cutting-edge technology that creates a digital replica of a physical entity based on advanced modeling technologies and real-time physical data [1].With the advent of 6G,there has been a call to establish DTs for geographically wide-areas(“DT-WA”) [2],which can fuse the physical and digital worlds to facilitate large-scale monitoring,prevalidation,prediction,and intelligent management in various fields,such as transportation,water resources management,city planning,building construction and emergency orchestration [3].For instance,DT-WAs have been built to forecast city flood [4] and forest fire [5].According to the International Data Corporation,the global investment in DT-WA is expected to reach$107.826 billion by 2025,with a compound annual growth rate of 34.13%over five years.
A critical component of DT-WA is the behavior model of the physical world,which can be used to pre-validate proposals and predict future states for advanced management.In particular,it is expected to be realized using an artificial intelligence(AI)model[6],which would be established in a distributed form with a large quantity of sub-models deployed on different edge servers,co-located with different access points(APs),so as to capture various locations in the widearea.Specifically,the AI model needs to incorporate a distributed updating process to maintain its predicting and simulation accuracy for the dynamic environment.That is,sub-models on different ESs should regularly update their parameters,more precisely the integrated learning networks(e.g.,deep neural networks),based on the collected local sensor data.However,due to the extensive coverage of DT-WA,the updating process of the whole AI model would consume a massive amount of energy.Nevertheless,the study of the updating process is still in its early stages,despite its great potential for wide application.
To address the energy issues in the updating process,we identify six distinct features in the AI model of DTWA:
• Sub-models quantity: The AI model consists of a large number of sub-models on different ESs to model every part of the wide-area.For example,a DT-WA for city flood predictions requires to deploy sub-models in various locations such as different river banks,buildings,roads,and mountain areas[4].
• Sub-models heterogeneous: Sub-models on different ESs would be heterogeneous.Their structures and learning goals may be different depending on their local features.For example,the submodels on ESs connected with APs in mountains may need to predict the future soil moistures,while river banks predict the water levels.
• Sensors heterogeneous: The updating process relies data from various kinds of sensors,such as monitors and thermo-hygrometers.They may have distinct communication requirements,such as enhanced mobile broadband(eMBB)and ultrareliable low latency communications (URLLC).Furthermore,different sub-models may rely on different types of sensors at varying levels.
• Sensors uneven availability: The distribution of heterogeneous sensors across different ESs is not uniform.Moreover,their availabilities are dynamically changing,determined by their current battery levels which are influenced by the sensor activations,transmitting powers,and the speeds of solar charging.Consequently,the size of collected local datasets on different ESs may vary,inducing dissimilar sub-model updating convergencies and energies.
• Neighboring similarity:Sub-models on neighboring ESs may exhibit similar updating patterns,due to the ensemble change of system environment.For example,sub-models for adjacent river banks and mountain areas may have partially similar model architectures to infer future water level or soil moisture based on the present air humid and monitoring image.It offers an opportunity for neighbors to partially share their updating parameters.
• Community benefit: Each ES needs to act on the basis of community benefit.Individual sacrifice is encouraged to minimize the whole system cost.It is different from traditional multi-users/ESs scenarios [7],where each entity wants to minimize its own cost while achieving a good social welfare.
Based on the above features,this paper proposes a distributed edge cooperation and data collection scheme to reduce the overall updating energy of DTWA.Considering the sub-models on adjacent ESs may exhibit similar updating trends,each ES can choose to become either an updating helper or a recipient of its neighboring ESs,based on the quantities of available sensors,environmental changes,and basic updating convergencies.ESs with more available sensors are more likely to become helpers to reduce the system energy,since larger collected datasets can assist sub-models to achieve higher updating convergency with lower computing energy [8].Each helper first activates some of its local heterogeneous sensors to collect sensor data and update its sub-model,then sends the updated sub-model parameters to its neighboring recipient ESs.Each recipient combines the useful part from its helper’s parameters with its local sub-model to increase its basic updating convergency.Then,the recipient ES only needs to further update its sub-model based on local sensor data to capture local features with reduced workload.This approach enables a helper ES to save the updating energy of several neighboring recipient ESs,which can reduce the overall system energy.
Moreover,to facilitate the ESs decision making process,we investigate a cooperation and resource allocation problem,with the aim to minimize the longterm system energy under high updating convergencies and low latencies.It is complex due to three reasons.Firstly,each ES’s action can have a ripple effect on many other ESs in the network,making it challenging for each ES to make optimal decisions with only local information.This is compounded by the large number of ESs with a random topology.Secondly,the activations of different types of sensors must consider their different impacts on the local sub-model,their availabilities and their influences on each other during wireless transmission process.Thirdly,the dynamic environment leads to varying updating similarities among neighboring ESs and dynamic updating workload for each sub-model.Meanwhile,the sensor battery levels are constantly changing.Each ES must consider not only the current situation but also the historical and potential future conditions when cooperating,activating sensors,and allocating resources.
In view of the above issues,we propose a distributed cooperation and resource allocation algorithm.First,the problem is reformulated as a decentralized partially observable Markov decision process(Dec-POMDP),where each ES needs to dynamically decide its cooperation identity,activate heterogeneous sensors,and allocate wireless and computing resources,based on its surrounding observations.Then,to reduce the problem complexity,we solve two child optimization problems to minimize the local computing energy on all ESs and the surrounding energy on helper ESs,respectively.After that,we design a distributed large-scale multi-agent proximal policy optimization algorithm to solve the Dec-POMDP.Simulation results show that the proposed scheme can effectively reduce the DT-WA updating energy compared with the baselines.
The contribution can be summarized as follows:
• The paper closes the gap of studying the updating process for AI model in DT-WA,and designs a cooperation and data collection scheme for it to reduce its overall updating energy.
• An optimization problem is carefully established,where ESs needs to dynamically adjust their cooperative identities,activate heterogenous sensors and allocate wireless and computing resources,with the aim to minimize the average long-term overall updating energy,under updating convergency and latency requirement.
• We propose a distributed algorithm to solve the problem.The original problem is transformed into a Dec-POMDP.Then,the Dec-POMDP is simplified by solving two child optimization problems.Finally,distributed large-scale multiagent proximal policy optimization algorithm is proposed for each ESs to individually optimize its action.
• Simulation shows that the proposed edge cooperation and data collection scheme can efficiently reduce DT-WA updating energy under high updating convergency and low latency compared with the baselines.
The remainder of our work is organized as follows.Section II gives the related works.Section III and Section IV gives the system model and problem formulation,respectively.Section V designs an algorithm to solve the problem.Simulation results and discussions are given in Section VI.Finally,we conclude this paper in Section VII.
II.RELATED WORKS
This section briefly summarizes the existing works of DTs in wireless networks,and the previous works on DT-WA.
2.1 Digital Twins in Wireless Networks
Existing researches in wireless communication field mainly studied DT for services and wireless networks.On the one hand,researchers have proposed several updating schemes for service DTs.They normally leveraged the federated learning (FL) to learn the common feature in different devices with similar DT model structures,to obtain global DT model for specific services(e.g.,traffic predictions)[9,10].For instance,authors in[9]proposed an asynchronous model update scheme to efficiently aggregate the global service DT on base station (BS) based on the local DTs trained on different IoT devices.On the other hand,researchers have leveraged network DTs to capture the real-time network states for resource optimizations[11,12].For example,authors in[12]proposed a DTassisted task offloading scheme,where BS can make optimal offloading decisions based on the network DT by obtaining the state of computation resource on different user devices.They rarely studied the updating process for network DTs,since network DTs are mainly consisted of DTs of man-made network elements and mobile devices [13].These DTs can be provided by manufacturers,which are comparatively more stable,controllable and predictable than the nature environment in DT-WA,therefore do not need frequent updating process.
In summary,service DTs usually assume similar model structures within networks,whose FL-based updating strategies can not be applied to DT-WA to update the heterogeneous sub-models in DT-WA.Moreover,network DTs do not need such frequent updating process as DT-WA.Therefore,their strategies are not applicable for DT-WA.
2.2 Digital Twins of Wide-areas
DT-WA has two basic functions,monitoring and modeling the physical world.On the one hand,to realize the monitoring function,researchers have explored various three-dimensional (3D) reconstructing technologies to highly restore the 3D state of the physical world in digital space [3].Others developed efficient data synchronizing schemes to collect massive physical data via wireless networks to synchronize the digital counterpart [14].On the other hand,to realize the modeling function,researches have explored various modeling technics for DT-WA[15].In particular,the deep learning algorithm has been seen as one of the most prevail modeling approaches[6,16].For instance,authors in [16] combined semantic knowledge with deep neural network (DNN) to presenting and reasoning the DT-WA,so as to identify events and make decision automatically.
However,the study for updating the AI model in DT-WA is still in its infancy.It is critical for the pre-validation and predicting performance in DT-WA,which has a wide potential use in various fields.To close the gap,this paper studies the updating process,and solves its energy challenge by designing an energy-efficient edge cooperation and data collection scheme.
III.SYSTEM MODEL
3.1 Preliminaries
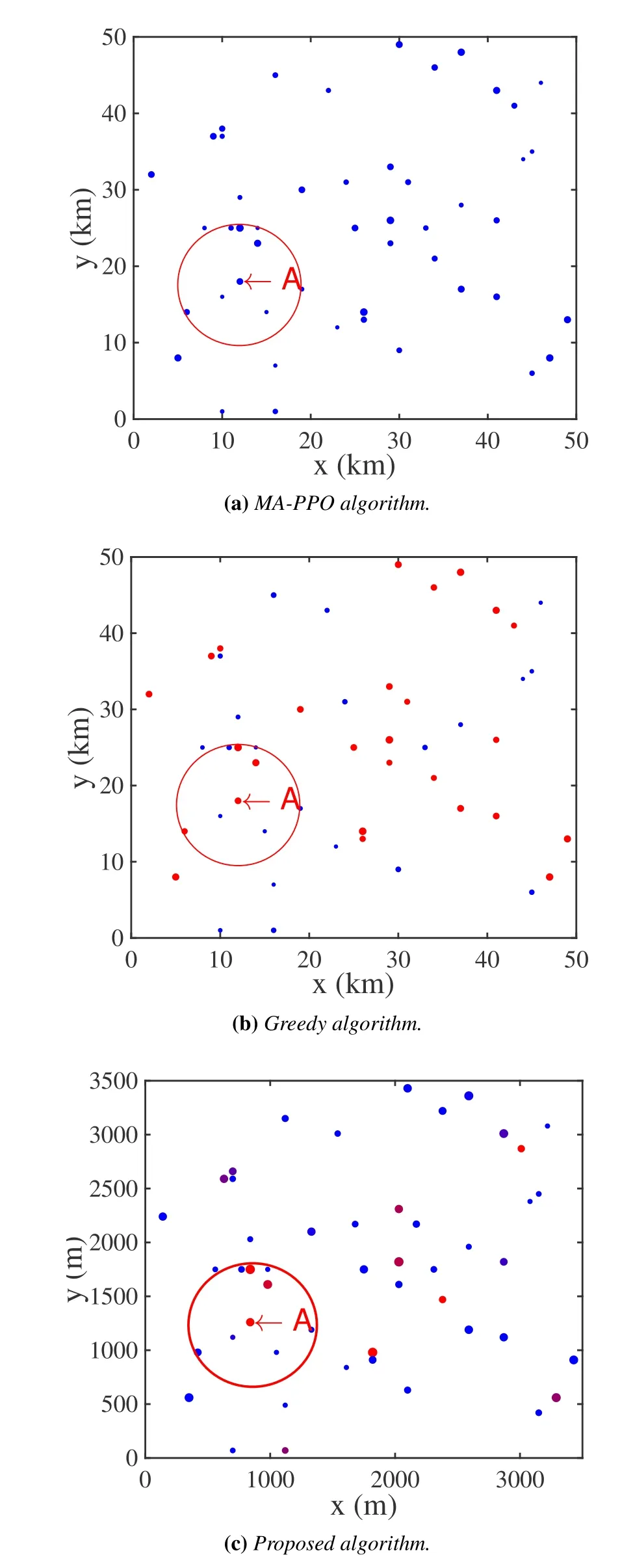
Large quantities of ESs co-located with different APs are distributed across the wide-area,which are denoted by a setF=(1,2,···,F).A DT-WA is established for the system,whose AI model is denoted byM.It is divided into multiple local submodels{Mi|i ∈F}deployed on different ESs for distributed updating,as depicted in Figure 1.Distance between two APs isdi,j(i,j ∈F).The set of neighboring ESs of ESiis denoted byBi={j|di,j Figure 1.Distributed edge cooperation and data collection for updating the AI model in DT-WA. Figure 2.Mean cooperative identities under different algorithms.Each point represents an ES,whose size is proportional to its local sensors quantity,which is randomly chosen from [Nmin,Nmax].The point color represents the longterm mean cooperative identity of each ES.It changes from black to red to present identity from recipient to helper. In each updating circle,each ES activates part of its available heterogenous sensors and collects sensor data through wireless communication.The collected data is used for updating its local sub-modelMi.The heterogenous sensors are divided into URLLC-type and eMBB-type depending on their transmitted datatypes,where we use superscript ‘B’ and ‘U’ to distinguish their variables,respectively.The multiplexing method for mixed eMBB and URLLC transmission is based on the well-known puncture approach[17].Specifically,each updating circle are divided intoKtime slots,denoted by{1,···,k,···,K}.Each slot is further divided into 10 mini-slots with a length ofTs(0.1ms).The eMBB-type sensors continuously transmitting its dataset within allocated bandwidth,whereas the URLLC packets can pre-emptively overlap the eMBB traffic in each mini-slot. 3.2.1 URLLC-Type Sensors To avoid co-channel interference,different ESs use orthogonal frequencies to collect datasets from its local sensors.The bandwidth used by each ES isB.We use a binary variable(t)to denote whether a URLLCtype sensornunder ESiconnected AP is available to activate,i.e.,having enough energy to work.If(t)=1,it is available,and vise versa.We use a binary variable(t)to denote whether sensornis activated.If(t)=1,it is activated,and vise versa.Only available sensors can be activated,i.e., It spontaneously generates and sends datasets to the local ES,with a probability ofqin each mini-slot.The packet size in one transmission is: wherelUis the number of samples in a dataset,sUis the bit size of one sample.Its transmission rate can no longer achieve Shannon capacity because of the finiteblocklength,where the instantaneous achievable rate is modified into[18]: 3.2.2 EMBB-Type Sensors The activated eMBB sensors equally divide the bandwidth of ESi.Therefore,according to the Shannon equation,the wireless transmission rate of each sensor under ESiis 3.3.1 ESs Cooperation Process During an updating circle,first,each ES chooses its cooperative identity (helper or recipient),which uses a binary variablemi(t)to convey.mi(t)=1 denotes the ES chooses to be a helper,whilemi(t)=0 denotes a recipient.All of the ESs that choose to be helpers are gathered into a helper setH(t)={i|mi(t)=1,i ∈K},which is unknown to any ES.Similarly,the ESs that choose to be recipients are gathered into a recipient setO(t)={i|mi(t)=0,i ∈K}.Then,all of ESs broadcast their identities to their neighboring ESs through wired link between APs,so that each recipient know the helpers in its neighborhoods.The recipient would randomly choose a helper from its neighborhoods,which is denoted by wherei ∈O(t) and=Bi ∩H(t).They would send an informing message to their helpers.Then,each helper is aware of its recipients,which can be represented by a set After that,helperi(i ∈ H(t)) updates its submodelMibased on its local data.Then,it shares the updated sub-model parameters with its recipients through wired channels with a negligible latency.Each recipientj(j ∈Gi(t))extracts the useful part inMi,and incorporates it into its old sub-modelMjto increase its basic updating convergency.Then,the recipient further updates its sub-modelMjbased on its local data. 3.3.2 Sub-Model Local Updating Process Helper ESs would start to update their local sub-model based on their heterogenous sensor data after their helper identities have been determined.Recipient ESs start to update their local sub-model based on sensor data after receiving their helpers’ sub-model parameters.For the local sub-model on ESi,its learning network (commonly a deep neural network) can be divided into two child networks that can be independently updated using eMBB and URLLC dataset,which are later integrated into an entire learning network using mixed eMBB-URLLC dataset to further update. Our goal is to let the ESs individually make decisions,e.g.,choosing cooperative identity,to update their local sub-models in DT-WA under updating convergency and latency requirements,with the aim to minimize the long-term system energy.Next,we give the mathmetical relationships between the decision variables with different performance metrics (i.e.,updating convergency,latency,system energy).Then,we give our optimization problem. At the beginning of each updating circle,each ES chooses to be a helper or recipient,and decides to activate local heterogeneous sensors.Then,they begin to collect the local data from their local sensors.After that,each helper ES updates local sub-model based on the local sensoring data.Then,it sends the updated sub-model to its recipient ESs.Each recipient partly combine its helper sub-model with its old sub-model and further updates it using local dataset. First,we give the heterogeneous data collecting delay of all ES.Considering the URLLC packets puncture the eMBB data streams in the wireless transmission process,the transmission delay of heterogeneous data is equal to the eMBB transmission delay.Besides,each ES would determine the received power for its local eMBB sensors,which is in the same value for different sensors.It leads to a same transmission rate(t) of all eMBB sensors under ESi,according to Eq.(5).The transmission delay would be wherelBis the number of samples in a dataset generated by a eMBB sensor,sBis the bit size of one sample. Second,we give the local updating delay of all ES,where each ES uses computing resources and collected data to update its sub-model parameters.On ESi,the computing workload of its sub-modelMicomprises three parts,which are eMBB and URLLC-data related child network updating and integrated updating,given as wherefi(t) is the allocated computation resource on ESi. Based on the above data collecting and ES computing delay,the overall updating latency of sub-model on every ES,including helpers and recipients,can be calculated by(12). In (12),the first line gives the overall updating delay of each helper ES and the recipient ES without matched helpers,the second line gives the delay of each recipient ES.The sub-model transmission delay between helper ES and its recipient ES can be omitted because of large wired transmission capacity. In the distributed DT-WA model updating scenario,we study the updating convergency of the sub-model on each ES.In each updating circle,due to the dynamic environment changes,the sub-model on an ES may not be able to faithfully replicate the behavior model of its physical environment.The mismatch is reflected in the basic updating convergencywhere) is the basic convergency factor.It is influenced by both the updating convergency in the last updating circle and the volume of environment changes after the latest updates.In particular,for recipient ESs,the basic convergency factor is also influenced by its helper sub-model,which could increase their original values.Commonly,the transition function of the basic convergency factor is unknown,due to the unstructured environment changes. In the local computing process of every ES,helper or recipient,the updating convergency depends on the sub-model structure,dataset dimension,and training iteration times.In detail,the updating convergency is jointly determined by the three sub-processes,including eMBB and URLLC-related child network updating and integrated updating,as given in Eq.(13). Each ES computing energy is determined by the computing resourcesfi(t),computing workloadCi(t)and computing time(t) in the local updating process,given by[21] whereκis the effectively switched capacitor coefficient.In thet-th updating circle,the system energy consumption is the sum of all ES computing energy We give the transition functions of the availability and remaining energy for URLLC and eMBB sensors. When an URLLC sensor is activated,its consumed energy in this updating circle is a fixed value().Therefore,the remaining energy of a URLLC sensornin the beginning of the(t+1)-th updating circle is The remaining energy of an eMBB sensornin the beginning of the next updating circle is The consumed energy on an eMBB sensor is dynamically changing in different updating circles.Therefore,working threshold can not be set by the energy consumption.To guarantee the energy consumption under the remaining energy on eMBB sensors,the following energy constraint should be met The aim of this paper is to minimize the average longterm energy of the overall DT-WA updating system,under updating convergency and latency constraint,formulated by From Eq.(9)and Eq.(13),we can see that more activated sensors would lead to a less computing workload under given convergency requirement.This insight indicates that ESs with more available sensors are more likely to be the helpers to reduce its surrounding energy.However,the cooperation process requires helpers to reduce their computing latency,so as to leave more time for their recipients to further compute.It would increase the computing energy of helper,inducing energy sacrifice. We employ multi-agent deep reinforcement learning(MA-DRL)to facilitate the ESs decision making process with the aim to minimize the system energy.Each ES deploys a DRL agent which dynamically generate decisions (e.g.,allocate resources) based on local environment (e.g.,number of available sensors) in the beginning of each updating circle,to collaboratively update sub-models for DT-WA in the dynamic environment.Each agent would experience two phases,including offline training and online implementing.In the offline training phase,each ES trains its agent’s actor network and critic network based on the interacting performance with physical environment.In the online implementing phase,each ES uses its trained actor network to generate actions. To reach the goal,first,we reformulates the original problem as a Dec-POMDP.Then,the dimensions of action and state vectors are reduced,where a child optimization problem is solved to minimize the local computing energy of each ES.After that,several constraint-released methods are designed to meet the sub-model updating convergency and latency requirements,where another child optimization problem is solved to minimize the surrounding energies of helper ESs.Moreover,we introduce the mean-field theory to propose a distributed large-scale MA-DRL which is feasible for the large-scale agent scenario.Finally,we give the overall algorithm and computing complexity. The original problem can be reformulated into a Dec-POMDP described by a tuple〈S,A,P,R,O,γ〉,where each element is given as follows: 5.2.1 State Space In the distributed DT-WA model updating process,the global state space is defined asS={Si|i ∈F},whereSiis the local state space of ESigiven by Eq.(22). 5.2.2 Action Space The global action space is defined asA={Ai|i ∈F},whereAiis the local action space of ESigiven by Eq.(23). 5.2.3 System State Transition Probability The transition probability of global state is related with the transition probability of local states: where the transition probability of local states is related with the local actions and local observations by Eq.(25).From the Eq.(25),the transition probability is unknown due to the random solar energy harvesting on sensors and randomly changing environment. 5.2.4 Reward Function Each ES can only know local and neighboring observations,based on which it learns to minimize the longterm average system energy.Considering each ES’s decision mainly influence itself and neighboring energy consumption,and the local reward function can only be designed based on the neighboring information,we design the local reward function to be which considers both the local and neighboring energy consumption.It reflects the main energy impact of each ES’s decision on system energy,and thus can lead the ESs to jointly achieve an approximate minimized overall energy. 5.2.5 Observations The joint observation space is a set of local observation space O={Oi|i ∈F},the latter can be defined to be the same as the local state spaceSi.Similarly,observation vectoroiis defined to be the same as local state vectorsi. 5.2.6 Discount Factor The goal of each agent is to learn policies to maximize the long-term discounted accumulated reward.Therefore,we set the discount factorγas 0.99 to make the agent’s goal consistent with aim to minimize the longterm system energy. We use two approaches to reduce the dimensions of the instant local observation vectoroi(t) and action vectorai(t),which could facilitate the latter learning process in the MA-DRL algorithm. 5.3.1 Replacing Large Sensor-Related Vectors into Single Elements 5.3.2 Replacing Iteration Number with Convergency Variable In action vector,the training iteration timeshave continues-like action spaces,which is extremely large.Moreover,it influences the reward through complex relationships in energy consumptions and updating convergencies,which makes it difficult for agents to learn to generate the optimal iteration number.To cope with the problem,we rewrite the constraintC3 into(28). We employ different constraint-released methods to meet different constraints in (35) to change the constraint-MG into MG. 5.4.1 Latency Constraint The “surrounding energy” refers to total computing energy of each helper and its recipients.To meet latency constraint,helpers need to determine the computing resource allocation for itself and its recipients.The detail is given as follows. Latency and energy are negatively correlated.The updating time of each helper is part of the updating time of their recipients.Take the helperiand its recipient setGifor example.We set the total updating latency of recipients equal to the latency threshold.Then,we formulate a child optimization problem to minimize the helper and its recipients energyby finding the optimal computing latency(t)of helperiin(36). Its derivative with respect to(t)is given in(37). In(37),the denominator is always positive because of the latency constraint in(36).Therefore,the sign of the derivative is determined by the numerator which is strictly increasing with the increase of computing latency(t).Moreover,the numerator becomes zero when the(t) is equal to the value in (38),which indicates the optimizing objective in(36)is a concave function,and (38) gives the optimal computing time of helperiand its recipients. 5.4.2 Accuracy Constraint For a helper,if its convergency action variable do not meet constraint,a punishment is multiplied with the reward function The computing resource needs to recalculated based on the rectified convergency variable and the optimal latency in(38). 5.4.3 Sensor’s Constraint Constraints in (27) includes sensors activating constraints and energy constraints.The activating constraints limit the sensor activating number under their available number.To deal with this constraint,we let the agent actor network generate normalized activating number,and scale it with the number of available sensors.The energy constraints convey that the energy consumption of sensors cannot surpass its remaining battery energy.The energy constraint of URLLC sensor has been met in its activating constraint. Multi-agent deep reinforcement learning (MA-DRL)has been proved as an effective approach to solve Dec-POMDP[23].In particular,multi-agent proximal policy optimization (MA-PPO) [23] has emerged as an outstanding algorithm to speed up the training convergence and obtain high rewards.However,it only work well under a small number of agents (2∼4)because of the dimensional curse,and relies on centralized training process which can cause heavy communication cost. To tackle the dimensional curse,we leverage the mean-field theory to modify the value function(critic network) and actor function (actor network) in MAPPO.Specifically,the mean-field theory conveys that the joint influences from other agents on one agent may be approximated as the mean influence from neighboring agents in a massive agents scenario.Inspired by this theory,first,we found that the value function[23]in MA-PPO can be reduced into a dependent variable of local observationoi(t)and mean neighboring observation in our content,which could dramatically reduce its input dimension,as proved by Eq.(42). Each ES deploys a PPO agent according to the proposed distributed large-scale MA-PPO algorithm.We change all of the action values into a(10×1)one-hot form(except for the binary variablemi(t)),as a ratio to the maximum action values,from 0/10 to 10/10.Each agent has a critic network and actor network,both of them are in fully-connected structure.The dimensions of the input,hidden and output layer in a critic network are=4,2=128×2,and 1,respectively,whose dimensions in an actor network are=42=128×2=32,respectively.For the activated functions,the output layer of critic network is activated by the Linear function,and actor network is Softmax function.Their hidden layers are activated by ReLU function.In addition,each agent would experience offline training and online implementing.The offline training phase is presented in Algorithm 1.First,to reduce the action and state space,we replace the large-dimensional variables of sensor related elements.Meanwhile,the training iteration variables are reduced by solving the neighboring energy minimization problem.Then,the algorithm alternates between sampling and training.During the sampling stage,each agent interacts with the environment,and uses several constraint-released methods to meet the DT-WA updating requirements.The training stage utilizes the sampling dataset to update the actor and critic network on each ES.In the online implementing phase,each ES would use its trained actor network to generate actions. To prove the capability of the proposed algorithm under large amount of agents,we randomly deploy 50 ESs co-located with APs in 3500×3500 square meter,compared with only 2∼4 agents in traditional MADRL.The path loss model between ES connected AP with sensors is 38.46+20 log10(d)[25].System parameters are given in Table 1.We choose four typical baselines for comparison: Table 1.System parameters. • MA-PPO:It is a well-known MA-DRL algorithm based on centralized training process.Existing works have used it to develop resource allocation strategies[26]. • Greedy,Random and Non-cooperative (NC)algorithms:The Greedy algorithm [27] sets the ESs with more than the average sensors to be helpers (“strong ESs”).The Random algorithm[27] randomly sets ESs to be helpers,while NC sets no ESs to be helpers. Figure 3 gives the convergency performances of the traditional MA-PPO and the proposed algorithm.It shows that the energy consumption of MA-PPO is approximately six times larger than the proposed algorithm when reaching convergencies,under different ES numbers and updating latency requirements.It is due to two reasons.First,the proposed algorithm greatly reduces the dimension of critic network,by condensing its input into most valuable information.This makes it easy to train the critic network.Second,neighboring information is provided to the actor network,which makes it easier to generate a good action that is beneficial for the whole community. Figure 3.Convergency performance. Figure 2 gives the mean cooperative identities of different ESs under different algorithms.It proves the inefficacy of MA-PPO in Figure 2a,where no ES chooses to be helper,no matter of whether it is proper for it to become a helper of its neighbors or not.On the contrary,both of the Greedy algorithms and proposed algorithm have multiple helpers,as shown in Figure 2b and Figure 2c,respectively.Specifically,Figure 4 shows that ESs with more local sensors while its neighbors having less sensors,more tend to become helpers.This mode can bring down system energy as explained in Subsection 4.5.Moreover,the proposed algorithm has much less helpers than the Greedy,according to Figure 2b and Figure 2c.Remember that a helper would sacrifice its own energy to reduce its surrounding energy(Subsection 3.3).It illustrates that the proposed algorithm learns to sacrifice ES with a higher efficiency. Figure 4.Mean cooperative identity vs.Different number of sensors under local and neighbor ESs. We take the ESA(pointed out in Figure 2)as an example to show the effectiveness of the helper sacrifice behavior.Figure 5 sequentially gives the mean energy consumption ofA,its neighbors (red circle in Figure 2)and the sum of two.When a“strong ES”becomes a helper,it can sacrifice its own energy to reduce the total energy of the surrounding area.In Figure 5,A’s energy consumption(360 J)in the proposed algorithm is much larger than the NC and MA-PPO algorithms(20 J and 30 J).However,it significantly reducesA’s neighbors energy to 1080 J compared with other algorithms.As a result,it leads to a smaller total surrounding energy(1450 J).The Greedy algorithm also sacrifices helperAto reduce its neighboring energy,whose total surrounding energy is smaller than NC and MA-PPO.However,in the Greedy algorithm,all of the“strong ESs”,no matter whether their neighbors have abundant sensors or not,are appointed as helpers.It leads to a low sacrifice efficiency and high neighboring energy. Figure 5.Contribution of A sacrifices for its surrounding energy. Figure 6 compares the mean overall system energy in different algorithms,under different numbers of APs/ESs and convergence latency thresholds.Specifically,different numbers of APs represents different resolutions and scales of the DT-WA system map.The proposed algorithm can obtain a smaller system energy than other algorithms under different network scales.Additionally,different DT-WA applications may have different requirements on the convergence latency.The figure shows that the proposed algorithm can achieve different latency requirements with the minimum energy consumption compared with other algorithms.Its well energy performance is due to the effective ESs cooperating process.That is,the proposed algorithm has a higher sacrifice efficiency than the Greedy,and thus has a smaller energy consumption.By comparison,the Random algorithm sometimes generates proper cooperation strategy,which makes its average energy a little bit better than NC algorithm.The MA-PPO keeps to generate poor cooperation strategies,which makes it behave even worse than the NC algorithm. Figure 6.System energies under different number of ESs and updating latencies in different algorithms. Figure 7 gives the mean transmitting power of eMBB sensors under different number of available heterogenous sensors.On the one hand,more URLLC sensors would lead to more punctures on eMBB traffics,which would reduce the time-frequency resources for eMBB traffics,and thus increase eMBB transmission delay.In this case,eMBB sensors would emit more transmitting power to keep its transmission latency acceptable.On the other hand,eMBB sensors evenly divide the wireless bandwidth for transmission.A large number of eMBB sensors would have less available bandwidth for each eMBB sensor.Thus,the transmission power needs to increase to keep the transmission rate and reduce transmission latency. Figure 7.Mean transmitting power of eMBB sensors under different number of available heterogenous sensors. Figure 8 gives the mean number of activated URLLC sensors under different number of available heterogenous sensors.Consistent to the insight mentioned in Subsection 5.3,the mean activated number approaches to zero when the number of available URLLC sensors is small and eMBB is large,and approaches the maximum number(available number)when the opposite situation happens.It is because that,in updating sub-models,the optimal training iteration times for URLLC-based child network and mixed eMBB-URLLC-based integrated learning network becomes zeros when the number of available URLLC sensors is smaller than eMBB sensors to a degree which is determined by the importance factor ofandin the updating convergency rate.Moreover,whenis larger than,it means the URLLC data is more important for the sub-model,which would require more URLLC sensors to activate,and it makes the dotted lines more wider on the head than the solid lines. Figure 8.Mean number of activated URLLC sensors under different number of available heterogenous sensors.Solid line represents =1,=5,while dotted line represents =1,=1. The paper closes the gap of studying the updating process for the AI model in DT-WA.It proposes a distributed cooperation and data collection scheme to solve the energy challenge in the updating process.In the scheme,ESs can share their updated sub-model parameters with neighbors to reduce the latter updating workloads and energy consumptions.Each ES needs to adaptively determine its cooperative identity,activate heterogeneous sensors and allocate wireless and computing resources to guarantee its local and neighbors updating performances.To minimize the overall updating energy,we formulate an optimization problem under updating convergency and latency constraints.Then,a distributed cooperation and resource allocation algorithm is proposed.First,the original problem is transformed into a constraint-MG.Then,the state and action spaces are reduced and several constraint-released methods are proposed.Finally,a distributed large-scale MA-DRL is designed by introducing the MF theory to optimize the ESs actions.Simulation shows the proposed cooperation and data collection scheme can effectively reduce the updating energy for AI model in DT-WA compared with baselines. ACKNOWLEDGEMENT This work was supported by National Key Research and Development Program of China(2020YFB1807900).
3.2 Dataset Collecting Process
3.3 Cooperation and Updating Process
IV.PROBLEM FORMULATION
4.1 Updating Latency
4.2 Updating Convergency
4.3 ES Computing Energy
4.4 Sensor Transition Functions
4.5 Objective
V.COOPERATION AND RESOURCE ALLOCATION ALGORITHM
5.1 Overview of Whole Algorithm
5.2 Dec-POMDP Formulation
5.3 Transformation in Observation and Action
5.4 Constraint-Released Methods
5.5 Distributed Large-Scale MA-DRL
5.6 Overall of Proposed Algorithm

5.7 Computation Complexity
VI.SIMULATION RESULTS AND DISCUSSIONS

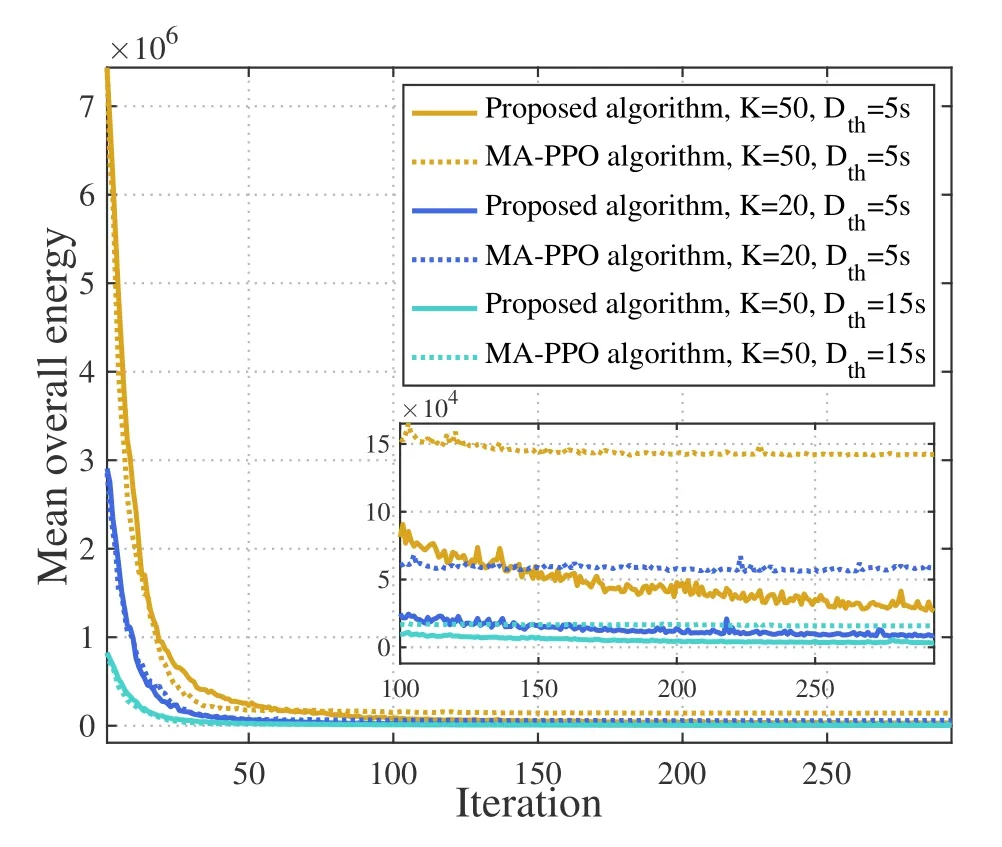


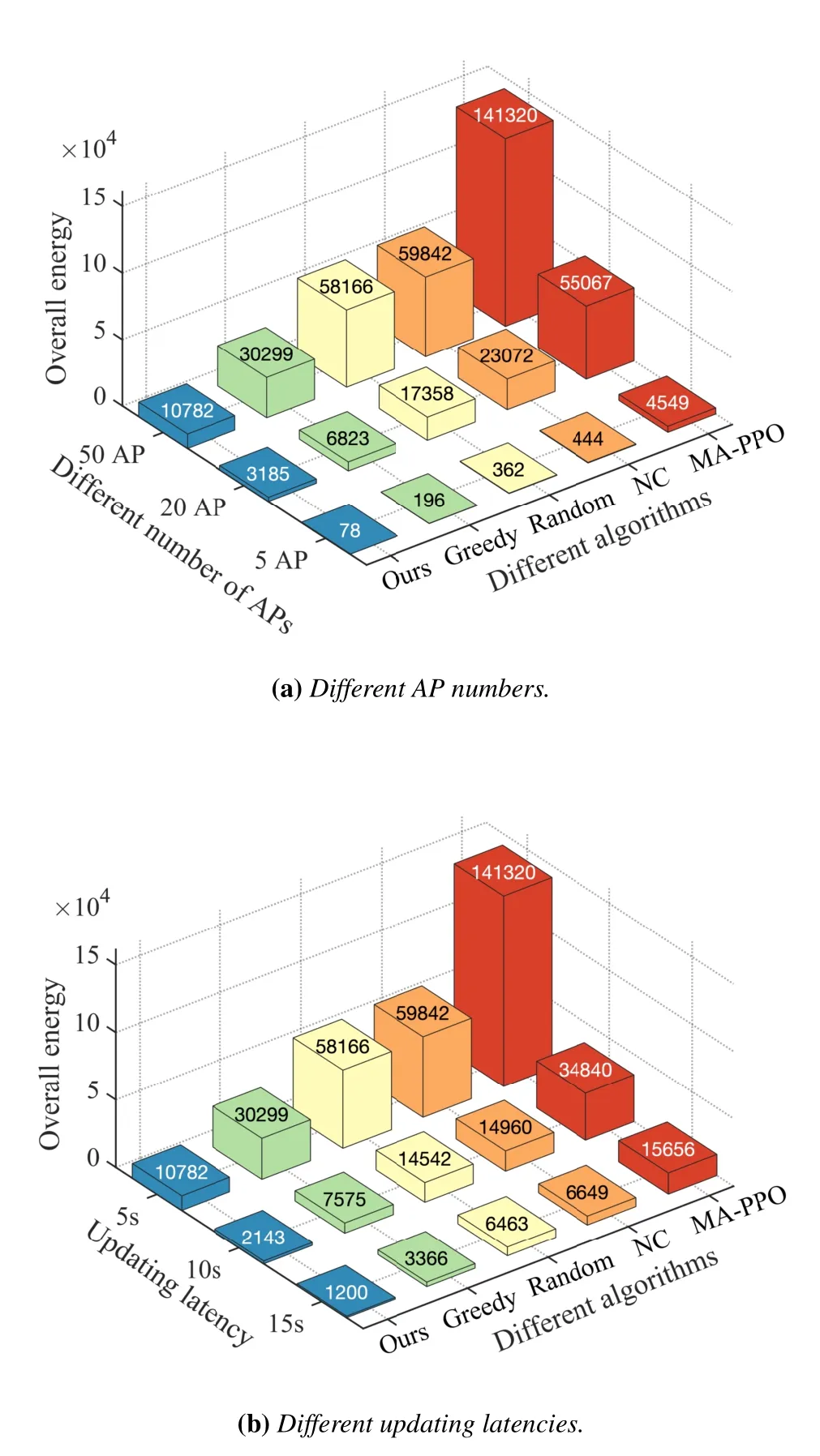

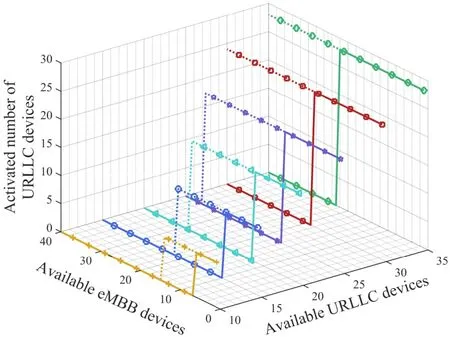
VII.CONCLUSION
杂志排行
China Communications的其它文章
- Group-Based Successive Interference Cancellation for Multi-Antenna NOMA System with Error Propagation
- Multi-Topology Hierarchical Collaborative Hybrid Particle Swarm Optimization Algorithm for WSN
- RFID Network Planning Optimization Using aGenetic-Simulated Annealing Combined Algorithm
- Power Allocation and Antenna Selection for Heterogeneous Cellular Networks
- Dielectric Patch Resonator and Antenna
- Discrete Phase Shifts Control and Beam Selection inRIS-Aided MISO System via Deep Reinforcement Learning
