设置开放性问题,提升学生的自主学习能力
2023-08-22沈元锋
沈元锋
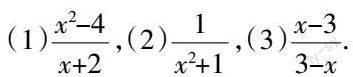
[摘 要] 自主學习能力是学生能够主动发现问题,并进行主动探究、寻找解题路径的学习能力. 自主学习能力是学生终身学习的基础,能够促进学生长远发展,是学生必备的关键能力之一. 开放性问题能调动学生的积极性,能激发学生参与学习活动的热情,能让学生在开放性的探索中获得思维能力的发展.
[关键词] 开放性问题;自主学习能力;学习兴趣
学会学习是新时期人才的必备能力之一,《义务教育数学课程标准》也将改善学生的学习方式作为教学的根本任务之一,因此教师要认识到培养学生学习能力的重要性,要在数学教学中通过教学活动引导学生掌握学习方法,体会数学思想. 具备自主学习能力是学生学会学习的标志. 在教学中设置开放性问题,能充分激活学生的思维,改善学生的学习方式,能让学习活动真正发生,从而提升学生的自主学习能力[1]. 下面,笔者结合多年的教学实践,从培养学生的自主学习能力出发,谈一谈通过设置开放性问题引导学生进行深度学习的教学策略.
教学案例
案例1 分式基本概念教学.
教师出示下面三个式子:
问题:请大家以学习小组为单位观察以上式子,写出具有意义的五个判断.
各小组讨论、交流之后,每组推荐一个代表在黑板上将本组的答案进行板书. 学生答案如下.
生1:当x的值为±2时,第(1)个式子的值为0.
生2:对于第(1)个式子,x的值为-2时,分母为0,分式没有意义,因此只有当x的值为2时,第(1)个式子的值才为0.
评价 这一知识点是考试中的热点,也是学生的易错点. 学生通过交流讨论和思维辨析,不仅得到了正确的结论,而且理解了分式的值为0的前提是分式有意义,由此学习的目标之一自然达成.
生3:第(1)个式子化简、约分后的结果为x-2.
评价 分式化简的知识虽然还没有学习,但是学生将分数约分的性质迁移到了分式中,实现了知识的迁移.
生4:无论x是何实数,第(2)个式子都有意义.
评价 学生已经发现无论x为何值,x2+1都不会等于0,因此分式始终有意义.
生5:无论x是何实数,第(2)个式子都不会等于0,且总为正数.
评价 这一判断相对来说更加高明,这说明学生的认识更加深入,不仅判断出了式子始终不会等于0,而且发现由于分母中含有x2,所以分式的值始终是正数. 这种思维的深度活动值得表扬.
生6:无论x是何实数,第(3)个式子的值都不会等于0.
生7:当x的值为0时,三个分式的值分别为-2,1,-1.
评价 生6使用了我们下一节课将要学习的分式性质和约分的知识. 生7解决了分式的求值问题. 点评时,教师选取了x=-2代入第(1)个分式化简后的式子x-2,得到答案为-4,与生7得到的结果进行对比,学生立刻对第(1)个式子中x不能等于-2有了更加深刻的理解.
设计意图 教材中的这部分内容主要是让学生认识分式是否有意义和分式的值为0这两个知识点. 笔者通过设计上述开放性问题,引导学生通过发散思维发现了更多的结论,调动了学生的积极性,使学生通过深度思维活动拓宽了学习视野,避免了单纯依赖教师的讲解,陷入被动学习的情况,促进了学生主动思考和探究,提升了学生的学习能力.
案例2 平面直角坐标系的教学.
问题1:请在坐标平面内画出以下各点.
A(2,0),B(4,0),C(-2,0),D(3,4),E(4,5),F(4,-5),G(-4,5),H(0,-4),P(-3,-4).
问题2:根据大家刚才所描的点,请每个小组的成员应用数学知识进行充分的联想和操作,并写下你们每个小组的发现. 看一看哪个小组发现的结论质量最高.
学生们在问题任务的驱动下,展开了激烈的讨论. 学生发现的结论如下.
第一小组:D,E两点在第一象限;点G在第二象限;点P和点F分别在第三象限和第四象限.
第二小组:从各个点分布在数轴上的情况来看,A,B两点在x轴的正半轴上;点C在x轴的负半轴上;点H在y轴的负半轴上.
第三小组:点E和点G、点A和点C分别关于y轴对称,点E和点F关于x轴对称.
第四小组:我们发现了线段AB,AC,BC的长分别是2,4,6;线段OD,PD的长分别为5,10;线段OE,OG,OF相等.
第五小组:我们从图形的角度观察有一些发现,如连接描的点之后可以得到等腰三角形HAC,等腰梯形ACGE;通过添加点Q(2,-5)得到矩形ABFQ.
第六小组:我们从线段之间的关系得到了一些结论,线段EG与y轴垂直,与x轴平行;线段EF与x轴垂直,与y轴平行;EG与EF垂直.
师:大家的独特发现让老师惊叹,不过我们要记住这么多的发现确实有些困难,所以在解决开放性问题时我们要遵循不同类原则. 现在请每个小组最多用三句话总结你们的结论,看看哪个小组的最终结论水平最高.
六个小组的同学纷纷调整结论,他们主要从下面几个方面来进行调整:
(1)说明点的位置所在的象限,同时指出坐标轴上的点不属于任何一个象限,并进一步说明了每个象限上的点具有的横、纵坐标特征.
(2)在指出点关于坐标轴对称的基础上,进一步指出关于原点对称的点,并总结了对称点具有的坐标特征.
(3)总结了点上下、左右平移的规律.
(4)指出经过两点的直线与坐标轴的位置关系,同时指出这些点的相关坐标特征.
(5)在发现相关三角形和四边形的特征中,进一步计算出相关图形的周长和面积,并且有些同学还总结出了计算平面内两点之间距离的方法.
師:大家的发现和总结都非常厉害,最后请大家把今天的学习内容整理一下. 如果大家还有其他的新发现,也可以记录在笔记本上. 希望大家有更多新的发现.
学生在课堂中的发现已经超出了教师的想象,在课后作业中学生又给了教师超乎想象的惊喜. 如:(2,2),(5,5),(-3,-3)三点的横、纵坐标相同,它们都在第一、三象限的平分线上;倘若这些点的横、纵坐标仅符号相反,那这些点都在第二、四象限的平分线上. 同时,学生还进一步总结出了到x轴、y轴距离相等的点的坐标特征.
设计意图 在本案例中,教师以平面直角坐标系中的点为基础,引导学生去发现这些点的特征以及它们之间的关系,学生在发现中自然地掌握了平面直角坐标系的相关知识和特征. 教师通过开放性的设问激发了学生的思维潜能,降低了问题的难度,使全体学生都能参与到学习活动中,突破了思维束缚,促进了学生自主学习能力的提升.
教学反思
1. 学生是学习的主人,学生学习的过程是将教学内容转化为自我认知的过程
学生是否真正参与学习活动,是否真正进行深度学习是评判学习效果好坏的关键. 所以教师在教学中要为学生创设自由思考的时间和空间,要鼓励学生积极思考、主动探究,要让学习活动真正发生[2]. 开放性问题能打开学生的想象力,能激发学生的积极性,能进一步培养学生的思维能力和自主学习能力.
教师要敢于将课堂还给学生. 在学生思考的过程中,教师要给予充分的信任,给予学生足够的时间去思考、尝试和探究,并进行适时的点拨与引导,而不是直接干预、阻断,或者代替学生思考. 静待花开也是一种教学方式,其能让学生深化认识,得到感悟和升华,从而提升学习能力.
2. 数学教学需要激发学生的学习兴趣,引发学生思考,使学习活动真正发生
教师要通过开展教学活动,引导学生在思考分析、题型强化和技能操练中思考问题,真正探寻数学的本质和规律,并在反思中总结和创新,激发思维活力,感受数学的价值.
开放性问题能使学生突破已有知识和经验的局限,实现思维的突破,能培养学生多角度分析问题和解决问题的能力,能打破时间与空间的限制,激发学生积极思考,并鼓励学生敢于质疑和批判,勇于打破权威,表达自己的见解[3].
虽然教材中的习题大多数是封闭性的,具有标准和统一的答案,但学生在生活中遇到的实际问题却大多是开放的. 因此,教师要做好学生的引路人,鼓励学生打开思路,进行多维思考.
总之,教师要为学生创设自主学习的氛围,鼓励学生独立思考探究,引导学生学会发现问题和分析问题,让学生在学习活动中提升思维能力,形成主动学习意识,培养创新思维.
参考文献:
[1]张才富. 一道中考题的多解分析与变式探究[J]. 中学数学教学参考,2021(09):55-57.
[2]厉兆云. 提高学生解题能力的几点尝试[J]. 教学月刊(中学版),2008(04):41-43.
[3]郭华. 深度学习及其意义[J]. 课程·教材·教法,2016,36(11):25-32.
