基于下记录值的逆指数分布模型的Bayes估计
2023-08-11席吉富罗子怡苏彦玉
程 丹,席吉富,罗子怡,苏彦玉,龙 兵
(荆楚理工学院数理学院,湖北 荆门 448000)
0 引言
逆指数分布是可靠性试验中一类重要的寿命分布,关于此分布的统计推断问题受到诸多学者的关注。文献[1]基于完全样本,在复合LINEX损失下研究了逆指数分布模型参数的Bayes估计,通过蒙特卡洛模拟对估计的优良性进行评估。文献[2]在刻度平方误差损失函数下讨论了逆指数分布参数的Bayes估计,通过随机模拟方法说明了刻度参数对Bayes估计的影响。文献[3]选取参数的先验分布为无信息先验分布,分别在平方损失、LINEX损失及熵损失下研究了逆指数分布参数的Bayes估计,并对三类损失函数下的风险函数进行了比较。文献[4]在平方损失、LINEX损失下讨论了逆指数分布参数的经验Bayes估计,通过随机模拟方式,论证了估计量的性质。文献[5]以逆指数分布模型为例,研究了损失函数及风险函数的Bayes 估计,说明了Bayes估计的合理性。国外也有许多关于逆指数分布统计性质的研究成果,如文献[6-8]。
设随机变量X服从参数为θ的逆指数分布,其概率密度函数及累积分布函数分别为:
(1)
(2)
其中,θ(>0)为未知参数。
根据式(1)及式(2),则可靠度函数R(t)及失效率函数h(t)分别为:
(3)
(4)
定义1 假设{Xn,n≥1}是独立同分布随机变量序列,令
U(1)=1,U(n+1)=min{j:j>U(n),Xj 记录值是一种特殊的次序统计量,由观测值和出现顺序决定,其在工程、寿命试验、体育、经济等方面都有着十分重要的应用。许多学者对记录值进行了统计分析并得到了一些重要的结论,文献[9]基于下记录值对广义指数分布进行了统计推断。文献[10]基于记录值讨论了Kumaraswamy分布参数的区间估计问题。文献[11-12]基于记录值用Bayes方法研究了模型参数的估计。我国也有一些关于记录值样本的研究成果,如文献[13-15]。但目前还未见到在下记录值下关于逆指数分布统计性质的研究成果,故对这一问题进行讨论。 设XU(1)=x1,…,XU(n)=xn是来自逆指数分布(1)的n个下记录统计量,根据文献[14]可得到似然函数为: (5) 将式(1)与式(2)代入式(5)可以得到: (6) 根据式(6),对数似然函数为: 根据文献[14]可知,统计量XU(n)的概率密度函数为: 因此对于逆指数分布模型来说,可以进一步得到XU(n)的概率密度函数为: 在Bayes统计推断中,需事先确定先验分布及损失函数,Gamma分布经常被用作未知参数的先验分布,因此取θ的先验分布为Gamma分布,其概率密度函数为: (7) 超参数a>0,b>0,Γ(·)表示Gamma函数。 在统计决策理论及Bayes分析中,平方误差损失函数是一种经常被采用的对称损失函数,其优点是可以较容易地计算出被估计量的Bayes估计。平方误差损失被定义为:LS(φ(β),δ)=[δ-φ(β)]2,其中δ是φ(β)的一个估计。 在平方误差损失函数下,φ(β)的Bayes估计为 : (8) 其中,Eφ(·)表示关于φ(β)的后验密度函数求后验期望。 平方误差损失函数是一类对称损失函数,过高及过低估计带来的风险是相同的。在某些情况下,高估与低估会有不同的估计风险,因此对称损失函数可能是不合理的。考虑一类非对称损失函数,即熵损失函数,它被定义为: 在熵损失函数下,φ(β)的Bayes估计为: (9) 根据式(6)及式(7),可得θ的后验密度函数为: (10) 根据式(10)可得以下定理: 证明:根据式(8)可得: 证明:根据式(9)可得: 由式(9)可得熵损失函数下h(t)的Bayes估计为: (i)在平方误差损失函数下未知参数θ的E-Bayes估计为: (ii)在熵损失函数下未知参数θ的E-Bayes估计为: 证明:(i)根据E-Bayes估计的定义,利用超参数a,b的概率密度函数,对θ的Bayes估计再求一次数学期望就可以得到θ的E-Bayes估计,因此在平方误差损失函数下未知参数θ的E-Bayes估计为: 类似地也可以证明(ii)。 利用频率方法已经得到了逆指数分布中未知参数的极大似然估计及一致最小方差无偏估计。利用Bayes方法得到了模型参数、可靠度及失效率的Bayes估计。针对具体的样本进行数值计算,文献[4]中给出了参数θ=2的逆指数分布样本:8.709 4,45.335 6,3.081 9,15.665 2,1.139 8,97.746 9,1.533 8,1.452 4,15.073 4,6.562 7,1.004 4,0.450 1,17.831 1,1.239 3,1.655 3,4.838 7,1.590 7,2.643 1,0.730 8,170.450 2。 由此可以得到样本总数为 5 的下记录值:8.709 4,3.081 9,1.139 8,1.004 4,0.450 1。 表1 Bayes估计 基于下记录值,讨论了逆指数分布参数、可靠度、失效率的极大似然估计及Bayes估计,研究了未知参数的一致最小方差无偏估计。根据E-Bayes估计的定义,讨论了未知参数在平方误差损失及熵损失函数下的E-Bayes估计。为了解各类估计的效果,利用数值例子计算出各类估计的值,对于同一个被估计量在平方误差损失函数下的估计值要大于在熵损失函数下的估计值。可以考虑计算可靠度及失效率的E-Bayes估计,由于没有显式表达式,可通过随机模拟的方法计算出近似值。利用本方法基于上记录值也可研究逆指数分布参数、可靠度及失效率的估计问题。1 频率估计

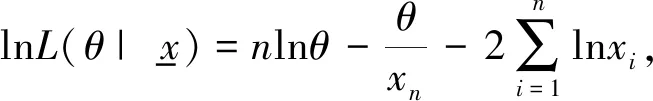
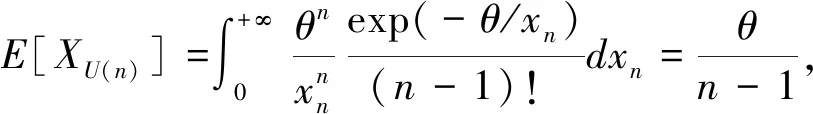
2 Bayes估计



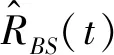
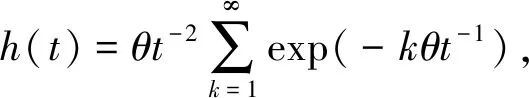












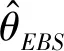
3 数值例子



4 结束语
