散乱点云的圆柱提取和拟合

周 颖 林 意

(江南大学人工智能与计算机学院 江苏 无锡 214122)

0 引 言

随着激光扫描设备在各个领域的应用,人们可以用较低的成本快速获取物体表面的三维坐标,其中对圆柱点云拟合的应用是工业上比较常见的问题。圆柱拟合在工业上的应用包括特征提取[1]、对象识别[2]、自主导航[3]、几何质量检测[4]、施工测试[5]等。目前,研究人员对圆柱拟合做了一系列的研究,解决了工业上的一些难题。常用的圆柱拟合方法归纳起来有:遗传算法[6]、高斯图法[7]、坐标转换[8]、圆度判别法[9]等。这些方法原理复杂、计算量大。对此,张益泽等[10]提出了任意初值的圆柱拟合方法,通过对传统的误差方程进行改进,减少了各参数之间的关联,在方程中赋予任意初值,利用附有条件方程的间接平差求解圆柱参数;刘支亮等[11]在文献[10]的基础上,提出了自适应调整权阵的稳健加权总体算法,以3倍准差为阈值,剔除粗差,构建稳健的最小二乘拟合算法。迭代计算对初值的要求很高,研究人员对迭代初值做了进一步的改进:Wu等[12]通过协方差估计点云的法向量,再根据最小二乘法来估计轴线方向向量;申旭等[13]提出了三点共线法求得直线方向向量,把直线方向向量作为初始值代入误差方程迭代求解。此外,Paláncz等[14]利用期望最大化和最大似然估计来寻找高斯混合分布情况下的圆柱参数;Al-Subaihi[15]提出了一种基于最小化正交平方距离和最小的圆柱拟合方法,即最小化点到圆柱的正交距离,并用梯度下降法求解;梁雪等[16]研究了一种一边拟合一边去噪的方法来获取圆柱参数,先随机选取一定量的点,根据圆柱面的方程拟合圆柱,再选取一个阈值,把每一个点代入方程,计算的结果与阈值相比较,若小于阈值,则为内点,否则为噪声点。以上算法大部分都需要迭代计算,计算量大,计算时间长,然而迭代对初始值的要求很高,容易陷入局部最优陷阱,对计算结果产生影响。

在工业测量中,受到场地和仪器的限制,很难采集到规则的没有噪声的点云。由于采集到的点云是杂乱的,不能对初始点云直接进行圆柱拟合,因此,本文先对点云进行预处理,采用统计滤波消除噪声点,然后用体素滤波器进行降采样[17],得到数目较少且没有噪声的点云。接下来通过区域生长算法对点云进行分割,提取分割后的圆柱点云,再进行圆柱面拟合。圆柱面可以看作是一组到定直线的距离为定值的点的集合,这一特征表明了圆柱需要7个参数来唯一确定,这7个参数分别是圆柱中心轴线的方向向量(a,b,c)、中心轴线上一点(x0,y0,z0),以及圆柱面的半径r,如图1所示,计算点到直线的距离,列出误差方程,利用奇异值分解求出轴线方向向量,再通过旋转,使得轴线与z轴平行,将点云平行投影到xoy平面,把三维问题转换为了二维平面问题,再根据最小二乘原理拟合圆求出半径。本文方法理论简单,易于实现,而且避免了迭代计算。

1 点云预处理

1.1 统计滤波器

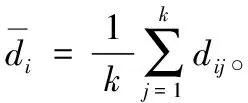
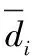
1.2 体素降采样

密集的点云在进行分割和特征提取的时候会增加计算难度和计算时间,用体素滤波器进行降采样能在减少点云数量的同时不改变点云的几何结构。体素是一个三维空间的小立方体,在进行降采样时,体素内所有的点用它们的重心来近似表示,最后,所有体素的重心组成滤波后的点云。如图2所示,图2(a)为创建的体积为l×l×l的包围盒,图2(b)为降采样后的用体素重心表示的点云。体素边长l的大小控制着采样率,当l过小,采样后的点云仍然密集,效果不明显;当l过大,采样后的点云过于稀疏,导致局部特征丢失。

(a) (b)图2 体素降采样示例

1.3 圆柱提取

点云分割有聚类分割[18]、区域生长[16]、RANSA方法分割[19]和语义分割[20]等,本节采用区域生长算法对点云进行分割从而提取圆柱。区域生成算法的基本思想是将具有相同特征的点加入到同一区域,本文的相同特征是指两个点云的法向量的夹角小于设置的平滑阈值。设一组点云数据为P={P1,P2,…,Pn},区域生成具体步骤包括种子点的选取、生长准则、终止条件。种子点选取的是曲率值最小的点,即最平滑的点。具体步骤如下:

(1) 对点Pi用kd_tree查找其邻域。kd_tree是一种带有约束条件的二叉查找树,每一级都在当前维度上划分开所有的节点,每个节点都表示一个超平面。kd_tree的示例如图3所示。

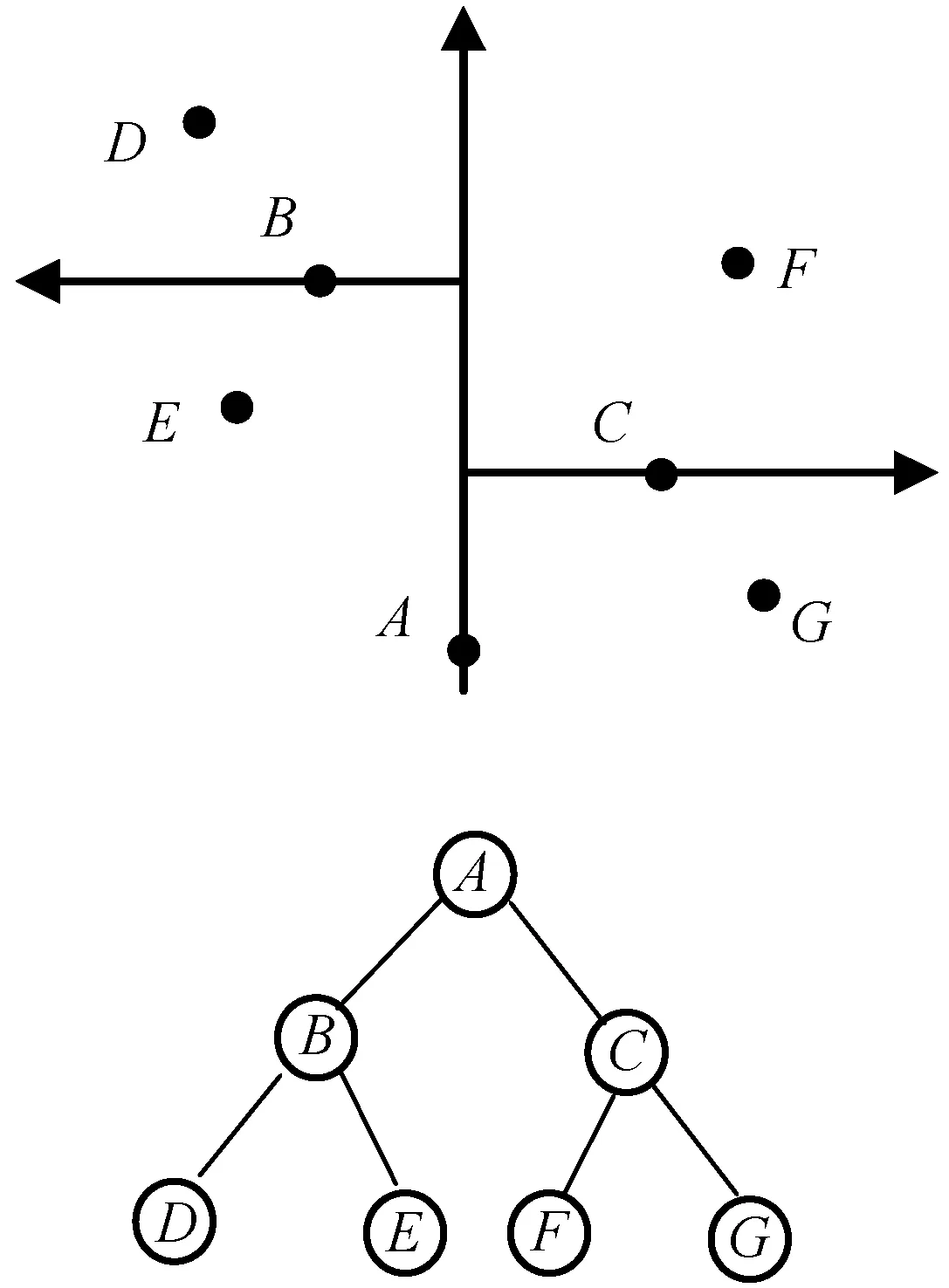
图3 kd_tree示例

(2) 设Ci为Pi的k个邻域点构成的协方差矩阵,则有:

假设求得式(3)的特征值满足λi1≤λi2≤λi3,对应的特征向量为vi1、vi2、vi3,则最小特征值λi1对应的特征向量vi1即为Pi的法向量,邻域曲率[21]为:

邻域曲率反映了该点的邻域所构成的曲面的弯曲程度,σi越小表明曲面越平坦越接近平面。计算出每一点的邻域曲率σi,对σi进行排序,选择σi最小的点作为种子点。

(3) 在进行区域生长的时候,计算邻域点与种子点的法向量之间的夹角,若夹角小于设置的平滑阈值,则把该邻域点加入到当前区域。

(4) 当所有满足条件的点都被合并到当前区域之后,在没有被合并的点中选择曲率最小的点作为种子点,返回第(3)步。终止条件是所有点都被合并。

(5) 点云分割完成之后,直接把圆柱点云提取出来即可。

2 圆柱拟合

2.1 直线拟合

设圆柱中心轴线所在的直线为L,L的方向向量为(a,b,c),对L的方向向量进行归一化处理,得到a2+b2+c2=1。设L上某一点的坐标为(x0,y0,z0),则L的标准式方程为:

把式(5)写成参数方程为:

式中:t为参数变量。则L可以表示为:

L=v0+Dt

(7)

式中:v0=(x0,y0,z0)T;D=(a,b,c)T。

图4 点到直线的距离

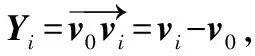
建立目标方程:

式中:n为测量点的个数。

首先,求初始值v0。对v0求导并令其导数为零:

故:

又有:

因此:

即证明了L过测量点的重心。

把式(9)展开用点的坐标表示:

(a(xi-x0)+b(yi-y0)+c(zi-z0))2]

(15)

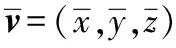
对各测量点去重心:

式(15)变形为:

对各参数求导并令其为0,变换成矩阵形式为:

对矩阵进行特征值分解,最大特征值对应的特征向量即为L的方向向量。

2.2 半径拟合

旋转点云使L与z轴平行,再将点云投影到xoy平面上,如图5所示,将三维问题转换为二维问题,再利用最小二乘原理拟合圆。

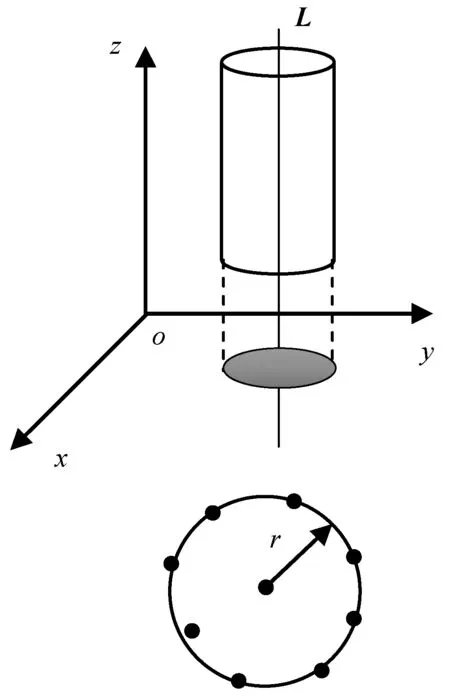
图5 拟合半径

首先将点云绕x轴旋转θ角度,使L与yoz平面平行,旋转矩阵为R1:

其中:

再将点云绕y轴旋转β角度,使L与z轴平行,旋转矩阵为R2:

其中:

设点云的半径为r,圆心坐标为(xa,ya),根据最小二乘原理写出误差方程:

对各参数求导并等于0,令:

变换为矩阵形式为:

(26)

解方程求出圆心坐标(xa,ya),代入求导公式中,求出r,再通过反坐标变换求出在圆柱上的圆心点。

3 实例与分析

为验证本方法的有效性,采用三维扫描仪对桌面进行扫描,对得到的数据进行处理,可视化如图6(a)所示。按照第2节提到的方法,首先对初始点云点云进行统计滤波去噪,本文选择的邻域点个数是100,标准差倍数是0.8,去噪后的点云如图6(b)所示,数目为130 251,可以看出,原始点云中的噪声点基本已去除,靠近圆柱边缘的点还存在小部分,在进行区域生长的时候会剔除掉。为了缩短后续区域分割的时间和提高圆柱拟合的效率,接下来对点云进行降采样,降低点云的密度。设置体素边长为0.03 m时,点云数目为18 428,如图7(a)所示,可以很明显地看到点云密度降低了,并且保留了点云的形状特征;设置体素边长为0.06 m时,点云数目为5 237,如图7(b)所示,点云更加稀疏,且形状特征没有发生变化。本文选用边长为0.06 m的体素进行降采样。

(a) 原始点云 (b) 去噪后的点云图6 点云滤波去噪

(a) 体素边长0.03 m(b) 体素边长0.06 m图7 不同边长的体素对点云进行降采样

在进行区域生长分割时,根据实际情况选择合适的曲率阈值和平滑阈值,本文中设置的平滑阈值为0.05π,曲率阈值为0.01,将点云分割成平面、圆柱和边缘噪声点,再通过设置最小簇类数目将噪声点剔除,分割完成之后,把圆柱点云提取出来,如图8所示。

图8 提取出来的圆柱点云

提取出圆柱点云之后,按照本文方法对圆柱进行拟合,求出的轴线方向向量为(0.025 31,-0.999 67,-0.005),拟合半径r=0.762 87 m,圆柱的轴线方程可以表示为:

式中:t为参数变量。

平面圆的圆度是指点到圆心的距离与半径之差,同理扩展到三维空间,圆柱的圆度[4]是指圆柱面上的点到中心轴线的距离与半径之差,计算结果如表1所示,图9为圆度折线。对圆度进行统计,圆度均值为-0.01 mm,标准差为0.45 mm。

表1 部分观测点的圆度值

图9 圆度折线

为了进一步验证本文方法的正确性和有效性,采用文献[4]中的算法和数据进行圆柱拟合,本文算法中的(x0,y0,z0)与文献[4]中的(x0,y0,z0)都表示轴线上一点,但是意义不同,所以没有可比较性,只需要比较另外四个参数值即可。表2是本文方法与文献[6]和文献[10]中方法的比较,图10是三种方法的圆度比较,可以看出,三种方法的差异是比较小的,且本文方法的圆度标准差略小,说明了本文方法的正确性。

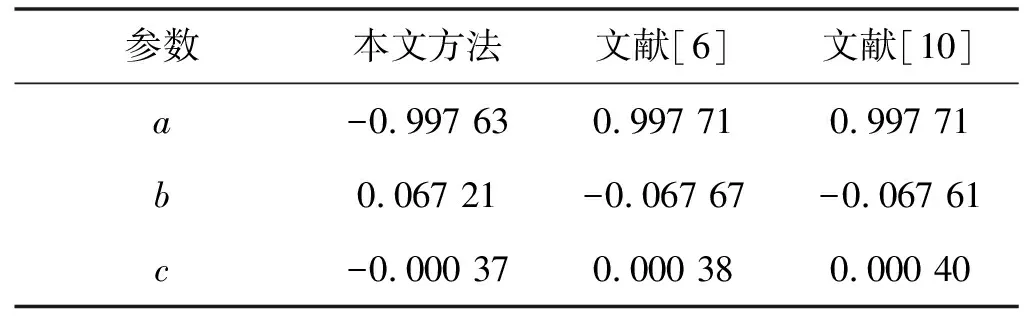
表2 与文献[6]和文献[10]结果对比

图10 圆度对比

4 结 语

本文介绍了从散乱点云中提取圆柱点云并进行圆柱拟合的一种方法。本文方法首先用统计滤波器和体素滤波器对点云进行预处理,然后采用区域生长算法对点云进行分割,得到拟合算法需要的数据,然后利用点到直线的距离建立方程,求出轴线,然后通过旋转和投影,将三维问题转换为二维平面问题,最后利用最小二乘法拟合出半径。本文方法原理简单,便于实现,而且具有很好的精度,最大的特点是避免了迭代。通过实验分析和比较,证明了本文方法的有效性和正确性。

在用滤波统计器进行去噪的时候,邻域点的个数和标准差倍数的选取对结果是有直接影响的,这里值得进一步研究。