面向温室移动机器人的无监督视觉里程估计方法

吴雄伟 ，周云成 ，刘峻渟 ，刘忠颖 ，王昌远

（沈阳农业大学信息与电气工程学院，沈阳 110866）

0 引 言

实时定位是温室移动机器人[1]实现导航，进而开展自主作业的关键。温室场景类似于室内环境，狭小拥挤，且植株行及金属棚架结构遮挡电磁信号，大田智能农机常用的卫星定位技术[2]难以在其内部进行有效工作。用导轨、道路[3]、垄沟、作物行[4]等特殊环境构型引导定位机器人，是常用的解决方案。然而铺设导轨会增加温室建设成本，用特定算法提取植株行等作为导航线的方法[4-6]，虽然能有效引导机器人作业，但导航线必须连续才能满足全局环境下的移动定位需求。LONG等[7]通过扩展卡尔曼滤波和自适应蒙特卡罗定位算法，集成超宽带、惯性测量单元和激光雷达等多种传感器，构建了温室机器人室内定位系统。多传感集成的方案可取得较高定位精度，但也会增加机器人开发成本。近年来，随着计算机视觉技术的进步，直接应用相机采集图像和视觉算法，通过连续跟踪机器人相对于出发点的位置及姿态（位姿）变化，实现移动定位的相关研究取得了一定进展[8-13]。相机价格低廉，如果能在算法上取得突破，该类技术可作为一种有效的室内定位方案。

视觉里程估计是同步定位与地图构建（simultaneous localizationand mapping, SLAM）系统的核心，后者使机器人能够依赖视觉传感器完成自主导航[14-17]，而前者的里程估计精度则直接决定了导航定位性能。目前，视觉里程估计的经典核心算法主要分为基于特征点提取与匹配的方法[8-11]，和基于光度误差优化的直接法[12-13]两大类。董蕊芳等[14]应用一种特征点法，融合多模态环境信息，实现了基于先验地图的机器人定位。在温室中，植株及建筑结构是主要场景物，其所成图像颜色、纹理通常较单一，描述图像局部特征的高可分特征描述子设计困难，同时该类方法只能得到特征点的稀疏深度（目标远近）值[8]，对于相对狭窄局促的温室环境来说，难以满足移动机器人的避障需求。直接法则建立在光度不变假设上，可获取场景稠密深度值，但该类方法需要逐帧优化求解图像深度及位姿变化，对计算资源要求高，且温室内光环境复杂，帧间图像可能会违反光度不变假设，使算法求解不稳定。

得益于生物神经网络在与环境交互过程中的持续学习能力，生物视觉系统在各种复杂条件下仍能进行良好的空间定位与深度感知。受此启发，深度学习技术逐渐被用于视觉里程估计任务上。ZHOU等[18]首先基于深度卷积神经网络（deep convolution neural network, DCNN），用无监督学习方法，联合训练深度和位姿估计网络模型，实现了基于连续图像的视觉里程估计，GODARD等[19-20]对模型进行了持续改进。周云成等[21]通过进一步在联合模型中引入时序一致性约束，探讨了其在温室移动机器人位姿跟踪方面的性能。该类方法应用DCNN的学习能力，可从大量图像样本中学习场景结构先验，克服了经典方法存在的一些不足。但由于位姿估计网络在推理过程中，直接用相邻帧图像作为输入预测帧间位姿变化，缺少必要的几何监督，因此此类方法一直受到尺度不确定性的困扰[22]，与特征法[8-11]相比，位姿估计偏差较大，定位精度不高。ZHAO等[22-23]将深度网络和光流网络结合在一起进行无监督联合训练，用光流建立的像素匹配关系来解决尺度不确定性问题，但该方法针对的是单目相机，只能获取工作场景的相对深度及位置变化，难以进一步应用于机器人的导航路径规划等任务上，且在推理应用中需要同时计算两个神经网络，资源需求量大。

鉴于温室移动机器人自主工作中，对绝对尺度视觉里程信息的实际需求，和现有深度学习位姿估计模型存在的尺度不确定问题，本文以双目相机作为传感器，提出一种基于无监督光流的视觉里程估计方法，用双目图像间光流计算场景稠密绝对深度，用相邻帧间可靠光流结合场景深度计算帧间位姿变换。构建约束光流模型的局部几何一致性条件，提高光流和位姿估计精度。并在种植番茄的温室场景中开展试验，验证方法的有效性。

1 基于无监督光流的视觉里程估计方法

1.1 技术框架

在温室移动机器人携带双目相机所采集并经立体校正的连续视频中，设t-1、t为相邻帧图像采集时刻，用I1、I2、I3分别表示t-1时刻左目图像和t时刻左、右目图像。设空间点P在I1、I2、I3上的投影点2D坐标分别为p1、p2、p3（互为匹配点），如双目相机内、外参矩阵K（含焦距f）、T（含基线距离b）已知，根据双目视觉原理，由p2、p3水平x坐标差值（视差d），可得P在t时刻左目相机坐标系下的深度值Z2=fb/d，进而可得其3D坐标P2=[X2,Y2,Z2]T=K-1Z2h(p2)，h(·)为齐次坐标转换。此时P2、p1构成一组3D-2D匹配，基于多组匹配，用n点透视（perspective-n-point，PnP）算法[24]可解算出I2至I1的位姿变换矩阵T21，即帧间位姿变换Tt→t-1。继而可知机器人相对于出发点的位姿变化Tt=ΠtTt→t-1，连续的Tt则构成了机器人运动轨迹，即视觉里程估计可转化为在图像间寻找匹配点问题。

本文通过构建基于深度学习的无监督光流模型，建立图像间像素级稠密匹配，以克服传统基于特征点匹配的视觉里程估计方法只能获取稀疏深度值的问题。首先用经过训练的光流估计网络（FlowNet），预测I1、I2间的前后向光流（图像间像素运动，即匹配点间的坐标差异）场。将双目图像间视差视为一种特殊光流，即进一步用FlowNet预测I2、I3间的双向光流场，其中在前向光流场W23中，表示像素在x方向运动的平面W23[:1]可视为该视差。由W23[:1]可得I2对应的稠密深度图D2，进而可恢复出I2各像素的点云3D坐标。进一步基于预测光流场，通过前后向光流一致性检查[25-29]，选择I1、I2、I3间的可靠匹配点集，构成多组3D-2D匹配，并用PnP算法求解帧间位姿变换矩阵T21。该方法的整体技术框架如图1，其在跟踪机器人位姿变化的同时，可获得前进方向温室场景的稠密三维结构信息，为避障等其他应用提供了可能。

图1 基于光流的视觉里程估计框架图Fig.1 Framework diagram of visual odometer based on optical flow

1.2 无监督光流模型

光流估计是图1技术框架的基础。温室场景及种植作物复杂多变，光流估计模型的普适性决定了本文方法的可用性。无监督光流模型[25-29]的学习过程只需用相邻图像作为训练样本，无需光流真值作为标签，本文用该类模型建立像素匹配，以持续支持在线学习、终身学习，适应不同类型的温室场景。为便于后续问题讨论，首先对无监督光流模型的基本思想做说明。设Wij=Φ(Ii,Ij;θ)为用深度神经网络构建的映射，以相邻图像Ii、Ij作为输入，预测前向光流场Wij，其中θ为Φ的可学习参数。根据Wij建立的像素匹配关系，有pi+Wij(pi) =pj，pi（位于Ii上）、pj（位于Ij上）为基于Wij建立的匹配点，通过从Ij上采样，可重构视图。与Ii在非遮挡区域应表观一致，用函数度量二者的差异（光度损失），以为优化目标，用大量相邻图像作为样本，可实现Φ的无监督训练。

式中α1=0.01、α2=0.05[26]。

用遮挡估计结果Mij，为重新定义前向重构光度损失，如式（2）所示。

式中ψ采用鲁棒性惩罚函数形式，其定义为，其中q=0.4、ε=0.01[27]，并用Mij(pi)排除遮挡区域。按生成Mij的相同过程，为Ij生成后向遮挡掩码Mji并定义后向光度损失ℓp,ji。进而以argmin(ℓp,ij+ℓp,ji)为优化目标，实现Φ的无监督训练，并用完成训练的Φ预测图像间光流。

1.3 光流估计网络结构优化

PWC-Net[31]是一种为有监督光流模型设计的神经网络，但其在无监督光流估计中也得到了广泛的应用[26-28]。本文以PWC-Net为基础，并参考近期无监督光流估计的相关研究进展[28-29]，对其结构做进一步优化调整后，作为映射Φ（光流估计网络）。该网络用DCNN分别提取相邻图像Ii、Ij的多层级特征图，构成6层特征金字塔（图2a）。基于各层级特征，用光流估计模块（flow estimation module, FEM）分别预测各层级光流场，l表示层号。FEM首先对l+1级光流场进行上采样，生成上采样光流场，基于该光流场，通过双线性插值在Ij的当前层特征图上采样重构出，用和Ii的当前层特征图计算代价体[31]，将代价体、、和作为一个稠密卷积网络的输入，做光流估计，输出当前层级光流场。用FEM逐级预测各层级光流场，直至，然后对其上采样，生成与输入图像同尺寸的最终光流场Wij。

图2 深度神经网络结构Fig.2 The structure of deep neural network

与有监督光流模型不同，无监督模型要预测双向光流来估计遮挡，计算量大。因此，为减少计算量，损失函数通常只设置在最终光流场上[25-28]，但这也使层级光流场缺少直接监督信号。JONSCHKOWSKI等[28]研究发现，由于缺少直接监督，PWC-Net的高层级特征图激活值普遍趋近于0，这将影响网络对层级光流的预测。本文用特征归一化来处理该问题，具体方法为：对各层级特征图和，用(V-μ)/σ进行归一化，V及μ、σ分别表示特征图及其均值与标准差。该处理可改变特征图的激活值分布，缓解激活值趋近于0的问题。PWC-Net的FEM只在第2层级中，用环境网络[31]对所预测的光流场进行精化。本文的FEM（图2b）则在每一层级中均采用环境网络精化光流，提升最终光流场Wij的预测精度，并用优化调整后的网络作为本文光流估计网络Φ。

1.4 局部几何一致性约束的提出

Φ的光流场预测精度，直接影响视觉里程估计性能。为提高Φ的训练效果，提升光流预测精度，本文根据局部图像I1、I2、I3所具有的几何特性，在argmin(ℓp,ij+ℓp,ji)目标基础上，进一步提出并构建3种局部几何一致性约束，以监督Φ的训练过程。为此，在训练中除用Φ预测I1、I2和I2、I3的双向光流场外，还用其估计I3、I1间的双向光流，共产生6个局部光流场（图3），并相应生成对应的遮挡掩码。

1.4.1 对极几何约束

对于由Wij（图3中任一光流场）建立的匹配点对pi、pj，根据对极几何，pi在Ij上的对应极线向量为lj=Fijh(pi) = [a,b,c]T，Fij为Ii至Ij的基础矩阵。pj应该在极线lj上，如不在，则其离lj的距离可用式（3）计算。

将距离超过阈值（本文设为0.1）的点，标记为外点，生成外点标记掩码，当时，，否则。此时可用式（4）计算外点距极线的平均距离。

式中ℓd,ij可称为极线距离损失，以其最小化作为Φ的优化目标之一，可使Wij中的外点逐步成为内点。

1.4.2 匹配点选择与基础矩阵求解

式（3）的计算需要基础矩阵Fij。假设Φ在训练过程中预测的Wij含有精确匹配（内点），只要从中筛选出这些点，即可用8点法[32]通过随机采样一致性（random sample consensus, RANSAC）循环求解Fij。精确匹配点对的双向光流应大小相同，方向相反，即具有一致性。首先定义式（5）来衡量匹配点对的光流一致性。

1.4.3 位姿变换矩阵求解与投影一致性约束

首先用Φ预测的视差W23[:1]计算得到I2的深度图D2，进而恢复I2像素的点云3D坐标。然后按求解基础矩阵的相同策略，基于一致性得分平面，从W23中选择I2到I3的精确匹配点集，进一步基于，从W21中选择I2到I1的精确匹配点集，用2个点集的交集，选择3D点云坐标和在I1中的2D匹配点，构建3D-2D匹配关系。由该关系，可用PnP算法[24]在RANSAC循环中求解I2至I1的帧间位姿变换矩阵T21。

在计算出D2和T21的前提下，根据多视几何原理，I2上的点p2在I1上的投影点可由式（6）计算得到[19]。

式中ℓe1为I2到I1的投影一致性损失，如果I2至I1的帧间位姿变换矩阵T21是精确的，则该损失值主要受W23和W21的精度影响。同理，由D2和相机的外参矩阵T，进一步计算I2到I3的投影一致性损失ℓe3，并令ℓe=ℓe1+ℓe3。以argminℓe为Φ的另一训练目标，会间接使光流场W23、W21具有一致性。

1.4.4 光流场一致性约束

在3幅局部图像中，像素在I2、I1间的运动（光流），等价于先从I2运动到I3，再从I3运动到I1，因此理论上光流场W21、W23和W31应满足W21(p2)=W23(p2) +W31(p3)，即这3个光流场应具有一致性，用惩罚函数ψ来度量等式两侧的差异，如式（8）所示。

式中ℓu2为光流一致性损失，M2(p2)=M21(p2)M23(p2)，即式（8）只考虑在I1、I2、I3上均可见像素的光流一致性。同理，光流场W12、W13和W32也应具有一致性，按式（8）相同方式计算一致性损失ℓu1，并令ℓu=ℓu1+ℓu2。以argminℓu作为Φ的训练目标，会使其预测的多个局部光流场具有一致性。

通过所选择的内点集计算基础矩阵和位姿变换矩阵，在对极几何和投影一致性约束下，Φ在训练过程中预测的光流场外点，将在多步学习中逐步成为内点，并在光流场一致性约束下，使该过程在6个局部光流场间传递。

1.5 金字塔层间知识自蒸馏的应用

在Φ预测的多层级光流（图2a）中，理论上最终光流场Wij应具有最高精度。为进一步解决网络训练中，层级光流缺少监督的问题，本文用最终光流场监督其他层级光流的预测。

知识蒸馏[33]是一种支持预测能力迁移的深度学习方法。本文借鉴其思想，将最终光流场蒸馏到其他层级光流上，称为金字塔层间知识自蒸馏。传统知识蒸馏方法通常用于网络间的知识迁移，金字塔层间知识自蒸馏则在同一个网络Φ内的不同层间迁移知识。具体方法为，以Wij作为伪标签，定义式（9）所示的金字塔层间知识自蒸馏损失，以该损失最小化为Φ的学习目标之一，实现层间知识迁移。

式中↓表示下采样，用于将Wij和Mij下采样到与的空间尺度相一致。Wij在下采样过程中需要将光流值缩小为原值的1/2l，同时用Mij将遮挡区域从知识迁移中排除。相对于将多种优化目标组成的损失函数直接设置在层级光流场上，层间知识迁移能以较小的计算代价，将最高分辨率和精度的最终光流场蒸馏到层级光流场上，而层级光流场精度的提高可能会通过FEM模块的逐级传递，进一步提高最终光流场的精度。

1.6 总损失函数定义与光流网络训练

1.6.1 总损失函数定义

组合6个局部光流场（图3）对应的光度损失、3种局部几何一致性损失和金字塔层间知识自蒸馏损失，同时为提高网络Φ训练的鲁棒性，引入基于边缘感知的光流场平滑损失ℓs,ij[34]和对光度变化不敏感的census损失ℓc,ij[25]。将各项损失按线性组合后，定义总损失函数ℓ，见式(10)。

式中λs等表示线性组合系数，分别设置为λs=0.05[34]、λc=1[25]、λt=0.01[29]、λd=0.1、λe=0.01[23]、λu=0.01[27]。最终以argminℓ为优化目标，训练网络Φ。

1.6.2 网络训练方法

基于PyTorch[35]，编程实现本文光流模型，用大量图像样本对网络Φ进行优化训练。用小批量随机梯度下降法更新网络参数θ，每小批含2个样本（由I1、I2、I3构成），学习率设为5×10-5。网络的输入图像尺寸设置为512×320像素。将网络的训练分为2个阶段，第1阶段在不包含局部几何一致性约束的情况下进行15代（epoch）迭代优化，第2阶段包含该约束后再进行多代训练，直至模型损失值收敛到稳定状态时为止。

1.7 评估指标

用多种评估指标评价本文方法的视觉里程估计性能。用估计光流和光流真实值间的端点误差（endpoint error,EPE）和错误率F1[29]来度量光流估计精度，2种指标值均越低，表明精度越高。

用视觉里程估计值和机器人真实运动轨迹，来计算相对位姿误差（relative pose error, RPE）和绝对轨迹误差（absolute trajectory error, ATE）[36]，衡量本文方法的位姿跟踪精度。RPE在局部范围内（设为1 m）[36]衡量误差，其包含相对位移误差（relative translation error, RTE）和相对姿态误差（relative rotation error, RRE）两部分。ATE则在整个运动轨迹内衡量误差。在计算RTE、RRE和ATE时，分别采用均方根误差（root mean square error,RMSE）和平均绝对误差（mean absolute error, MAE）2种方式，各指标值均越低，表示位姿跟踪越精确。

用像素p的估计深度与真实深度zp的平均相对误差（mean relative error, Rel）、平方相对误差（squared relative error, Sq Rel）、RMSE和lg化RMSE（RMSE1g），以及阈值限定精度[19]来衡量本文方法的深度估计性能，误差越低、阈值限定精度越高表示性能越好。阈值限定精度指满足δ < ωτ的像素所占的比例，其中ω=1.25、τ∈{1,2,3}[19]，δ通过式（11）计算。

2 试验系统及数据集构建

2.1 试验系统

用轮式移动机器人（速度0～0.8 m/s，可定速行进）作为底盘载具（图4），开展数据采集及验证试验。该设备采用Nvidia Jetson AGX Xavier作为控制主机，运行Ubuntu 18.04和ROS系统，可远程遥控行进。视觉传感器采用Stereolabs ZED 2k双目相机，水平前视安装于底盘上部的托架上，离地高度约1.2 m，并通过USB串口接入控制主机。相机单目分辨率为1 920×1 080像素，采样频率为15帧/s，配套软件工具提供了焦距、主点坐标和双目基线距离等参数，由这些参数可得相机内、外参数矩阵K、T。

图4 轮式移动机器人及试验场景Fig.4 Wheeled mobile robot and test scenario

本文光流模型在预先完成训练和测试后，再部署于移动机器人上，用于视觉里程估计。在配置有Intel Xeon E5-2 630 v4处理器，Nvidia Tesla K80计算卡，128 GB内存，Windows Server 2019 R2操作系统的计算机上进行光流模型的训练和测试。

2.2 温室双目视频数据采集

于2022年10—11月，在沈阳农业大学教学科研基地，某种植番茄的辽沈IV型节能日光温室内，开展双目视频数据采集。此阶段番茄处于坐果期，植株吊蔓生长，株高1.5～2.2 m，株距约0.3 m，行距约1.2 m。在晴朗天气的10:00—16:00采集数据，通过遥控，使机器人在株行间和其他行走通道上行进，并通过双目相机采集视频。将采集的长视频分割成小序列，每序列含200帧双目图像，共500个小序列。随机选择400个序列作为训练集，用于光流模型训练，其余100个用作测试集。

2.3 光流真实值获取

针对测试集，进行图像间光流真实值获取。SIFT算子对光照变化、旋转、缩放等具有鲁棒性，对测试集的每个序列，用该算子提取I1、I2、I3的特征点，用k近邻算法匹配各图像间特征点，通过比率测试和交叉过滤初步滤除误匹配，通过在RANSAC循环中求解基础矩阵并应用对极几何约束，进一步删除外点，最后用人工逐帧走查方式去除剩余的误匹配，用余下正确匹配点的坐标计算图像间稀疏光流，并将其作为光流真实值，共获取8.52×107个真实值。用测试集及其光流真实值评估本文光流模型的光流估计精度。

3 结果与分析

3.1 无监督光流模型的有效性分析

无监督光流模型的光流预测精度直接决定基于图1技术框架的视觉里程估计性能。为提高光流预测效果，本文在现有方法[25-29]基础上，构建了局部几何一致性约束，并优化调整了光流估计网络等，首先通过试验，分析各处理的有效性。

3.1.1 损失项的有效性分析

光度损失和光流场平滑损失最小化一直是无监督光流模型的主要优化目标，以此为基准，在网络Φ相同的前提下，通过逐步启用总损失函数ℓ的其他损失项，构建了6种网络损失模型，分别命名为I、II、III、IV、V、VI，各模型对应的损失项线性组合系数设置如表1，其中模型I的损失项构成同文献[34]，II的构成同文献[25]。用温室双目视频训练集训练各模型，进而用测试集及其光流真实值评估各模型对应网络的光流估计精度，每个试验重复3次，结果如表1。

表1 不同网络损失模型的无监督光流估计精度Table 1 Unsupervised optical flow estimation accuracy for different network loss models

表1数据表明，各损失项对提高光流估计精度均是有效的。模型I只含光度和光流场平滑损失，II在其基础上增加了census损失，该处理使4项光流端点误差EPE和错误率F1显著下降（P＜0.05），表明census损失在该任务中是有效的。census损失通过比较重构图像与目标图像的census特征，可克服光度变化对损失度量的影响，使模型训练更具鲁棒性。III在II基础上增加了金字塔层间知识自蒸馏损失，该损失项使各项误差均显著降低（P＜0.05），其中相邻帧间光流的EPE降低11.76%，双目图像间光流的EPE和F1分别降低11.45%和1.76个百分点。最终光流具有最高分辨率，这有利于光度损失发挥监督作用，获得精度更高的光流场，再将此光流场蒸馏到中高层光流上，相当于间接将含多种约束的无监督损失函数作用于中高层上，提高了中高层光流的估计效果，进而促进了依赖中高层光流的最终光流场精度的提高。

IV、V、VI在III的基础上逐步引入3种局部几何一致性约束损失项，结果表明，整体上各项误差逐渐降低。IV和III相比，6项EPE和F1指标均显著下降（P＜0.05），表明对极几何约束可显著提高模型性能。V在IV基础上增加了投影一致性约束，该处理使前者的2项F1相比后者显著下降（P＜0.05），其余指标有所下降，表明该约束对提高光流估计精度也是有效的。VI和V相比，6项EPE和F1指标均显著下降（P＜0.05），表明光流一致性约束能有效降低预测误差。同时比较VI和III，前者的EPE下降8.89%，的EPE和F1分别下降8.96%和1.23个百分点，进一步表明局部几何一致性约束对提高模型光流预测精度是有作用的。局部几何一致性约束使Φ在训练过程中，应用当前估计的部分可靠光流值，计算图像间的几何关系，并进一步应用该几何关系约束模型，使其估计的外点逐渐成为内点，从而在整体上提高了模型的光流预测精度。总体上，本文构建并引入的多个损失项均能有效提高无监督光流估计性能。

3.1.2 网络结构有效性分析

进一步分析本文光流估计网络的优化调整对光流预测的作用。以PWC-Net为基准，对其使用特征归一化处理后，构成网络Φ0，进一步在各层级FEM中使用环境网络精化层级光流，则构成本文网络Φ，各网络均采用模型VI的损失函数。用温室双目视频数据集训练并测试各网络光流估计性能，同时测试各网络计算速度，结果如表2。

表2 不同网络结构的无监督光流估计精度Table 2 Unsupervised optical flow estimation accuracy for different network structures

由表2可知，网络结构对模型性能影响显著。Φ0在PWC-Net基础上对金字塔层级特征进行归一化处理，该处理使6项EPE和F1指标均显著降低（P＜0.05），其中的EPE降低了12.50%，的EPE和F1分别降低了7.25%和0.99个百分点，归一化处理使Φ0的计算速度下降了1.28%，但光流估计精度有较大提升，表明特征归一化对提高模型性能具有显著作用。由于特征归一化可改善高层特征图激活值分布，较好地避免了激活值偏低对FEM预测高层光流场的影响，从而通过提高高层光流场的预测效果，进而提高了最终光流场的预测精度。Φ在Φ0基础上，使用环境网络精化金字塔各层级光流，该处理使各项误差显著下降（P＜0.05），其中双目图像间光流EPE下降4.69%。用扩张卷积构建的环境网络有效扩大了卷积感受野，这使其可以在更大尺度上应用环境信息来精化光流运动，进而提高了光流估计效果。在各层级FEM中运行环境网络，需执行大量的计算，因此与Φ0相比，Φ的计算速度下降了14.24%，在应用中，可根据实时性和精度的平衡，决定是否启用精化过程。总体上，本文对网络结构的优化调整，对提高模型光流预测性能是有效的。按文献[31]方法对Φ估计的部分局部光流场进行可视化，结果如图5。

图5 局部光流场示例Fig.5 Examples of local optical flow field

从图5b、5c可以看出，光流模型估计出了相邻帧图像上不同像素的光流变化。由于双目图像间光流只是像素在水平方向上的运动，因此光流场W23和W32的颜色值应是单一的，图5 d和5e的结果与此相符，即本文模型是可以同时用于估计帧间光流和双目图像间光流的。

3.2 温室移动机器人视觉里程跟踪试验验证

3.2.1 视觉里程跟踪试验验证方法

用完成训练和测试的光流估计网络Φ（模型VI）作为FlowNet，基于ROS，编程实现图1框架所示视觉里程估计系统，并部署在轮式移动机器人上，框架中的各步计算均实现为ROS节点。系统除完成计算外，也将运行过程中的跟踪计算结果（深度图、帧间位姿变换矩阵等）连同双目视频帧，以文件形式存储于系统中。于双目视频数据集采集所在温室相邻的日光温室内，开展视觉里程跟踪验证试验。两个温室种植作物相同、管理模式相似。机器人采用遥控方式行进，行进中，系统持续在线跟踪机器人运动轨迹。每次跟踪，机器人分别以0.2、0.4、0.6和0.8 m/s不同的速度匀速前进，共跟踪了20条轨迹，每个速度分别对应5条轨迹，轨迹长度为15～70 m不等。每次跟踪后，从机器人系统中下载跟踪结果及对应连续视频帧。对连续视频帧做进一步处理，用2.3节方法获取图像间稀疏光流真实值，进而用1.1节方法计算稀疏深度真值和机器人位姿变换。该处理在文献[21]移动距离和角度变换已知的测试集上的相对误差均低于0.17%，因此可将其获取的位姿变换作为真实值，用于分析本文方法的视觉里程跟踪性能。

3.2.2 与现有方法的比较

为验证本文方法的性能，首先和现有的一些优秀基准方法进行比较，具体包括UpFlow[29]、Monodepth2[19]和ORB-SLAM3[8]，其中UpFlow是一种在交通数据集上取得优异性能的无监督光流模型，Monodepth2是一种基于无监督学习的深度和位姿联合估计模型，ORB-SLAM3是一种新近提出的用稀疏特征点实现视觉里程跟踪的SLAM系统方法。用温室双目视频训练集，分别训练UpFlow和Monodepth2，并按图1技术框架实现基于Up-Flow的视觉里程估计系统，用该系统、Monodepth2模型和ORB-SLAM3方法分别以离线方式，对视觉里程跟踪试验后下载的各轨迹连续视频帧进行视觉里程估计。由于移动机器人的计算资源无法满足同时运行多种方法，所以采用离线方式，以保证不同方法估计的是相同的机器人运动轨迹。用稀疏深度真值和机器人真实运动轨迹，对本文在线跟踪结果及其他3种方法的离线估计结果进行误差分析，结果如表3和表4。

表3 不同方法的位姿跟踪性能比较Table 3 Accuracy comparison of different methods on pose tracking

表4 不同方法的深度估计性能比较Table 4 Accuracy comparison of different methods on depth estimation

由表3数据可知，不同方法的位姿跟踪性能差异显著（P＜0.05）。在UpFlow、Monodepth2和本文方法在内的3种基于无监督学习的方法中，本文方法具有最高的跟踪精度，其在6项误差指标上均显著低于其他2种方法。就相对位移误差RTE指标而言，与UpFlow相比，本文方法的均方根误差RMSE和平均绝对误差MAE 2种统计结果分别降低9.52%和9.80%，与Monodepth2相比，则分别降低43.0%和43.21%。相对于Monodepth2，基于无监督光流的UpFlow和本文方法具有更好的位姿跟踪性能。Monodepth2的位姿估计网络在联合训练时，会受深度估计网络的约束，但在推理时仅有相邻帧作为输入，受尺度不确定性影响，帧间位姿变换估计往往精度较低。基于光流的位姿变换估计，则应用由双目和相邻帧间可靠光流构建的3D-2D匹配关系，求解帧间位姿变换，其在训练和应用中持续受到几何约束，无尺度不确定性问题，因此具有更高的位姿跟踪性能。对比本文方法和ORB-SLAM3，后者各项误差均显著低于前者（P＜0.05），但两者各项误差无数量级差异，另外本文方法能应用估计光流计算场景稠密深度和三维点云，进而可得场景三维结构，这是后者所不具备的。

由表4可知，UpFlow和本文方法在各项深度估计误差上均显著低于Monodepth2（P＜0.05）。由于Monodepth2的位姿估计网络受尺度不确定性影响，在联合训练中，该影响将会传递给深度估计网络，降低了其深度预测性能。本文方法的深度估计相对误差Rel为5.28%，与Monodepth2和UpFlow相比，分别降低2.90和0.99个百分点。ORBSLAM3只能提取、匹配稀疏特征点，无法与本文方法获取的稀疏深度真值相对应，因此未能评估其深度估计性能。对比本文方法和UpFlow，前者在3项深度估计误差和1项阈值限定精度上显著优于后者（P＜0.05），其他3项指标无显著差异，表明前者具有更高的深度估计精度。本文构建了局部几何一致性约束，优化调整了网络结构等，有效提升了模型光流预测效果，进而提高了基于光流的位姿跟踪及深度估计精度。总体上，本文方法能够跟踪机器人运动轨迹并估计场景深度，且具有较高的性能。

3.2.3 运动速度对机器人位姿跟踪性能的影响

机器人运动速度会影响帧间光流大小和相机成像质量，为分析运动速度对位姿跟踪性能的影响，进一步比较本文方法对前文视觉里程跟踪试验中，不同速度下机器人运动轨迹的跟踪精度，结果如表5。

表5 不同运动速度下的位姿跟踪性能Table 5 Pose tracking performance under different motion speeds

表5数据表明，机器人运动速度对本文方法位姿跟踪性能具有显著影响（P＜0.05）。在运动速度为0.2 m/s（记为慢速）时，跟踪性能相对较低，为0.4 m/s时，性能有所提高，为0.6 m/s时，本文方法具有最小的跟踪误差，为0.8 m/s（记为快速）时，各项误差迅速升高，跟踪性能变差。机器人运动速度决定相邻帧间的位姿变化大小，慢速运动时位姿变化小，快速时变化大。由于帧间光流估计存在着一定误差，该误差对基于光流匹配的微小帧间位姿变换矩阵的解算精度影响较大，对较大位姿变换矩阵的求解则影响较小。当机器人快速行进时，容易造成图像运动模糊和抖动，且帧间光流迅速变大，增加了模型光流预测难度[37]，从而使基于光流的位姿跟踪性能下降。就试验而言，本文方法在机器人以0.6 m/s速度运动时，具有最好的位姿跟踪性能。

3.2.4 分辨率对位姿跟踪性能的影响

本文光流模型在训练时，采用512×320像素的固定大小图像作为输入。在机器人视觉里程跟踪试验中，系统也将视频图像调整为该分辨率后输入模型。进一步采用本文方法，改变光流模型的输入图像分辨率，以离线方式对视觉里程跟踪试验后下载的各轨迹连续视频帧进行视觉里程估计，用于明确模型对不同分辨率输入图像的适应性，并分析分辨率对位姿跟踪性能的影响，结果如表6。

表6 不同输入图像分辨率的位姿跟踪性能Table 6 Performance of pose tracking with different input image resolutions

表6数据表明，用固定分辨率图像训练光流模型，在推理时改变分辨率，基于该模型的视觉里程估计系统仍能有效跟踪机器人运动轨迹，说明本文方法对分辨率变化具有鲁棒性。随着分辨率增大，位姿跟踪各项误差逐渐下降。当分辨率增加时，图像保留了更多的局部细节信息，利于模型提升光流估计精度，进而提高系统的位姿跟踪性能。同时，相同的光流误差对高分辨率图像间的位姿变换矩阵求解的影响也小于低分辨率图像。当图像分辨率为832×512像素时（限于计算设备存储约束，未能对更高分辨率进行分析），本文方法在1 m范围内产生的RTE绝对误差均值MAE不高于0.036 m（3.6 cm），相对姿态误差RRE的MAE不高于0.023 rad（1.3°），与448×256像素分辨率相比，图像接近放大2倍，这2项误差则分别下降33.33%和25.81%。图像分辨率对位姿跟踪性能具有显著影响，分辨率越大，跟踪精度越高。

3.2.5 轨迹跟踪与深度估计图示

用832×512像素分辨率图像作为光流模型输入，用本文方法，对部分视觉里程跟踪试验中不同速度下的机器人运动轨迹进行离线跟踪，结果如图6。

图6 不同行进速度下的轨迹跟踪示例Fig.6 Examples of trajectory tracking at different motion speed

由图6可以看出，本文方法可有效跟踪机器人的运动轨迹。图中各条跟踪轨迹与对应的真实轨迹在初始段吻合程度均较好，随着跟踪距离延长，也会逐渐出现偏离现象。

从图中可以看出，不同株行间的局部跟踪轨迹与真实轨迹的长度吻合程度较好，即局部轨迹误差较小，表6的指标值也说明了这一点，但随着误差累计，特别是姿态误差的累计，跟踪轨迹与真实轨迹之间的偏离逐渐增大。在机器人沿道路直行时，在15 m行进范围内，不同速度下跟踪轨迹与真实轨迹的一致性均较好。图6也表明，运动速度对轨迹的跟踪精度产生了较大的影响，在0.2 、0.8 m/s速度下，均较快地产生了轨迹偏离。

进一步选取视觉里程跟踪试验中，1条速度为0.6 m/s的视频序列，从中截取2段机器人在某株行间行进的小序列，其中一段由北向南行进，此时机器人逆光前行，另一段由南向北，即顺光行进。用本文方法以离线方式跟踪2个小序列的轨迹，基于视差W23[:1]计算各帧左目图像深度，进而恢复各帧点云，基于，保留其中得分为前20%的点云，并通过各帧相对于首帧的位姿变换矩阵Tt，将点云坐标变换到首帧对应的左目相机坐标系（设为世界坐标系）下，同时将跟踪轨迹点投影到首帧图像上，可视化结果如图7。

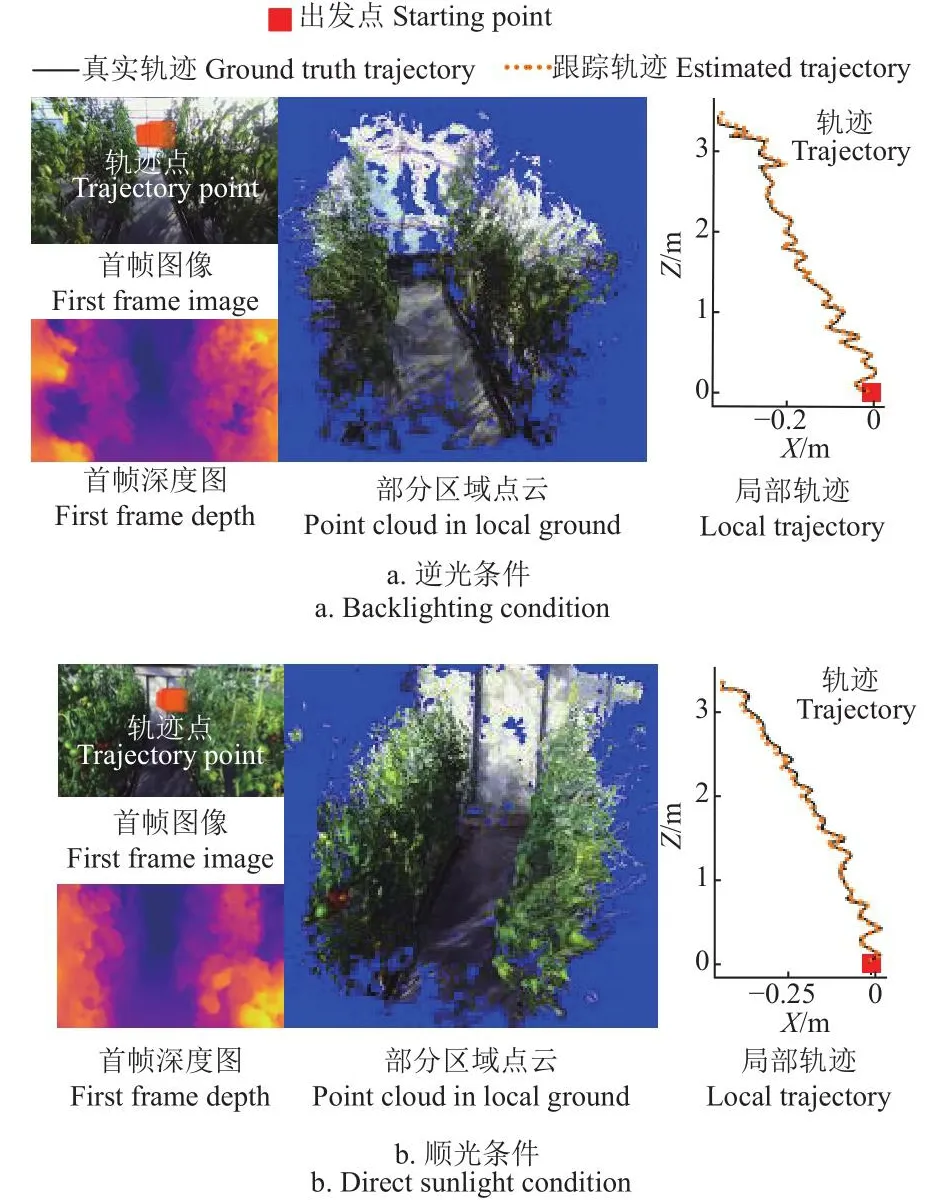
图7 局部区域内的视觉里程估计Fig.7 Examples of visual odometry application in local ground

由图7可以看出，在逆光和顺光条件下，小序列首帧图像对应的深度图，很好地反应了场景的景深变化，也清晰地刻画出了株行间的通道。由各帧深度图恢复的点云，在变换到世界坐标系下后，很好地反应了株行间局部区域的三维结构。通道地面和顺光条件下所见温室后保温墙对应的点云分布平滑，两侧植株点云结构清晰，通道空间内未见其他杂点，这表明将本文方法估计的深度信息用于机器人避障、环境地图构建[16]等也是可行的。从图中也可以看出，在局部区域范围内，跟踪轨迹与真实轨迹的吻合度较高，在机器人行进中，相机的左右摆动，在跟踪轨迹上也有较好的体现。与顺光条件相比，逆光条件下的相机成像质量相对较差，图像模糊，但本文方法仍能较好的跟踪机器人运动轨迹并恢复场景三维结构，表明该方法具有一定的鲁棒性和光环境适应性，本文可为温室移动机器人视觉系统设计提供一定参考。

4 结 论

本文提出一种面向温室移动机器人的无监督视觉里程估计方法，并在种植作物为番茄的日光温室场景中开展了试验验证，主要结论如下：

1）所构建的局部几何一致性约束能有效提高无监督光流模型精度，帧间和双目图像间光流端点误差EPE分别下降8.89%和8.96%。金字塔层间知识自蒸馏损失可显著降低光流估计误差，帧间和双目图像间光流EPE分别降低11.76%和11.45%。

2）对光流估计网络的层级特征图进行归一化处理，使网络计算速度下降1.28%，但光流估计误差也显著降低，其中帧间和双目图像间EPE分别降低12.50%和7.25%。

3）实际视觉里程跟踪试验结果表明，与基于UpFlow光流模型的视觉里程估计相比，本文方法相对位移的均方根误差和平均绝对误差分别降低9.52%和9.80%，与Monodepth2相比，则分别降低43.0%和43.21%，与ORB-SLAM3相比，本文方法的位姿跟踪精度相对较低，但优势在于能够恢复场景稠密深度，这为机器人避障提供了可能。本文方法的深度估计相对误差为5.28%，显著优于比较方法。

4）位姿跟踪精度受机器人运动速度影响，在0.2 、0.8 m/s下的位姿跟踪性能显著低于0.4～0.6 m/s速度下的性能。随着输入图像分辨率的增加，位姿跟踪精度逐渐提高，当分辨率为832×512像素时，该方法在1 m范围内跟踪的相对位移MAE不高于3.6 cm，相对姿态MAE不高于1.3°。

该研究可为温室移动机器人视觉系统设计提供技术参考。