基于参数循环算法的HMCVT燃油经济性多参数优化

梁 丽 ，李青涛 ，谭芸颖 ，杨兆虎

（1.西华大学机械工程学院, 成都 610039；2.西华大学现代农业装备研究院, 成都 610039）

0 引 言

液压机械无级变速器以其传递功率大、无级调速范围宽等优点被广泛应用于农业机械、建筑工程机械以及军工设备上[1-2]。同时，国家在农业生产方面对拖拉机的性能提出了更高的要求[3]。燃油经济性作为拖拉机作业的基本要求，成为人们关注的焦点[4-5]。

近年来，有不少国内外学者对拖拉机无级变速箱的最佳经济性控制策略进行了研究。TAKIYAMA等以经济性为目标，研究了变速器和发动机的联合控制策略[6-7]。DEBAL等根据已有的经济性、动力性变速控制策略，结合加权的方法实现车辆综合调控[8]。MACOR等研究发现通过变速器和发动机协同控制，可有效提高车辆的平稳性与经济性[9]；徐立友等研究了通过调节无级变速系统速比使发动机工作在最小燃油消耗率点，提出了拖拉机HMCVT的传动系统匹配策略，给出了实现拖拉机最佳动力性或经济性的调节规律[10]；王光明以车辆最佳燃油经济性为目标，考虑变速器效率的影响，以提高变速器效率的方法来提升拖拉机整机的经济性[11]；张明柱等考虑HMCVT传动效率存在差异的特点，分别以发动机和拖拉机燃油经济性最佳为指标，对比一元调节和二元调节四种控制策略下拖拉机的燃油经济性，发现以拖拉机燃油消耗为指标的二元调节变速控制策略燃油经济性更佳[12]；黄薛凯等研究了以发动机转速与变量泵排量比为控制变量的二元调节的控制策略[13-14]。从国内外对燃油经济性无级变速控制策略的研究现状可知，大多研究是以发动机和变速比为主要变量的二元调节，其中变速比仅跟随排量比变化而变化。但近年INCE等发表的最新HMCVT研究表明，在HMCVT中采用多种参数不同的齿轮行星排，根据工况不同选择合适的特性参数和排量比可保证高效传动[15]。LIU等研究了多行星排特性参数对传动系统的影响，得出拥有多个特性参数的行星排系统的加速性能和燃油经济性都有所提高[16-18]。目前，一种特性参数连续可变的滚子行星排传动系统被提出[19]，且被验证具有较大的速比范围和较高的传动效率[20]，但连续可变行星比的加入会影响系统的传动效率，进一步影响整车经济性。因此，本校提出一种单行星排特性参数可连续变化的传动系统，考虑在加入连续可变行星比这一参数上，进一步完善HMCVT燃油经济性变速控制策略。结合行星比连续可变的液压机械无级变速传动系统，提出拖拉机最佳燃油经济性评价指标；然后根据拖拉机整机调控的无级变速控制规律实现发动机和HMCVT工作点的多参数调节；以中小型拖拉机为例，利用参数循环算法，求算出拖拉机在任意工作点下的最佳发动机转速转矩、HMCVT的最佳排量比和最佳行星比，并从传动效率和变速比分布方面对燃油经济性的多参数调控效果进行验证。

1 拖拉机最佳燃油经济性评价指标

比油耗(gT)是指拖拉机完成单位作业量时发动机所消耗的燃油量[21]。对于在田间进行犁耕作业的拖拉机来说，主要功率输出是牵引农机具，一般以拖拉机的牵引功率代表拖拉机的输出功率，因此采用比油耗gT作为拖拉机经济性评价指标，计算式如下：

式中ge为发动机燃油消耗率，g/(kW·h)；ηT为拖拉机牵引效率；ηz、ηl分别为中央传动机构效率和履带车辆的履带驱动段传动效率，通常为常数；ηb为HMCVT传动效率；ηδ为滑转效率；ηf为滚动效率；ηδ、ηf主要取决于地面属性和牵引负载[22-23]。对于确定工况下地面属性和牵引负载不能改变，无法通过调节速比和发动机工作点改变ηδ、ηf。因此在研究拖拉机经济性最佳变速控制策略时，主要考虑HMCVT传动效率ηb，使得ge/ηb最小。

1.1 发动机有效燃油消耗率

发动机有效燃油消耗率ge与发动机转速ne(r/min)、转矩Te(N·m)相关[24]。以BM58G型柴油发动机为例，额定转速为2 400 r/min，额定功率为58 kW，根据发动机试验数据[25]拟合得到发动机燃油消耗率为

1.2 HMCVT传动效率ηb

由HMCVT传动原理图1可知，HMCVT在工作时分别由液压变速路径和机械变速路径传递功率，其中汇流行星排是由一米尔纳牵引式无级变速器Milner CVT[26-27]改造而成的滚子行星排，简称MVPT(multi-roller variable planetary train，MVPT)，一种行星比k可在1.5～2.0间连续变化的传动系统[20]。因此，实现变速传动系统速比连续变化不仅是调控变量泵的排量比，还可协同控制牵引式行星排的行星比k。

图1 HMCVT传动原理图Fig.1 Transmission principle diagram of hydro-mechanical continuously variable transmission(HMCVT)

由图1可知，HMCVT的类似于闭式行星齿轮传动，在计算HMCVT传动效率时需考虑结构性的功率循环、MVPT传动效率及液压变速路径传动效率影响，本文采用啮合功率法[28-29]计算HMCVT的传动效率ηb。

综上可知，HMCVT传动效率ηb与HMCVT变量泵排量比e、牵引式行星排行星比k、发动机转速ne、转矩Te有直接关系，简记为

当拖拉机工作负载变化时，发动机和HMCVT的工作点均发生变化。此时ge、ηb发生较大变化，针对发动机和HMCVT工作点进行调节，使ge/ηb最小，可实现拖拉机燃油经济性最佳。但连续可变行星比的加入会影响ηb，进而影响拖拉机整车燃油经济性，因此针对拖拉机发动机和HMCVT的调节便转化以发动机转速转矩和HMCVT变量泵排量比和行星排行星比的多参数调节。

2 多参数无级变速控制

2.1 多参数无级变速控制基本原理

调控时是否具有可靠的控制参数与合理的控制原理，主要取决于变速规律制定的合理与否，同时，变速规律对拖拉机整体性能也有重要影响。为了实现拖拉机经济性最佳，需要根据拖拉机的作业特性制定出最佳变速规律。

根据拖拉机最佳经济性指标分析确定HMCVT的无级变速规律，最佳燃油经济性多参数调控通过发动机和HMCVT协同实现。其中HMCVT的控制包括变量泵排量比和牵引式行星排行星比调控，因此实现拖拉机经济性最佳的无级变速控制规律是：拖拉机进行牵引作业时，在负载特性场内，先由拖拉机目标车速v(km/h)和牵引阻力Ft(kN)确定拖拉机的实际工作点(v，Ft)；再结合滑转率δ确定拖拉机的理论行驶车速；再进一步求出在HMCVT输出特性场内的工作点(nb，Tb)；然后根据该点(nb，Tb)，求解出使得ge/ηb最小的HMCVT最佳变量泵排量比、最佳行星排行星比和最佳发动机转速、最佳发动机转矩，根据得到的参数结果控制拖拉机的发动机转速转矩、泵-马达系统的排量比及MVPT无级变速系统的行星比，实现拖拉机最低燃油消耗的无级变速，具体控制流程如图2所示。

图2 拖拉机最佳燃油经济性控制流程Fig.2 Control process of optimal tractor fuel economy

目标作业车速v由驾驶员给定，牵引阻力Ft由传感器测得，将数据输入至电子控制单元，再由电子控制单元将信号分别发送给发动机电子油门控制机构、变量泵排量比调节机构和牵引式行星排行星比调节机构，三者根据接收信号分别将发动机转速转矩、泵-马达系统的排量比和牵引式行星排的行星比调节到最佳，在实现拖拉机设定目标车速的同时在相应负载工况下保持整车经济性最佳。

2.2 基于循环算法的控制参数求解过程

根据变速控制规律和控制过程可知，对于拖拉机在负载特性场内的任意工作点(v，Ft)，当排量比e和行星比k依次连续变化时，会产生一系列发动机工作点(ne，Te)与之对应，但其中只存在一种情况使得ge/ηb最小，因此需要对发动机和HMCVT的控制参数进行优化，且这种优化属于设计阶段的参数优化，实时控制阶段不需再进行优化。

根据拖拉机经济性影响因素[30]及ge/ηb最小，提出以下目标函数：

式中nemin、nemax分别为发动机怠速和最高空载转速，r/min；Telim为发动机限定转矩，N·m；emin、emax为HMCVT的变量泵排量比上下限，一般取-1～1；kmin、kmax为MVPT的行星比上下限，取1.5～2.0；Pemax为发动机最大功率，kW。

采用参数循环算法[12]优化相应参数，以拖拉机目标车速v、牵引阻力Ft、HMCVT变量泵排量比e和行星排行星比k为输入参数，以发动机转速ne、转矩Te和HMCVT变量泵排量比e和行星排行星比k为控制参数，求算出最佳控制参数，其基本步骤如下：

1)根据拖拉机目标车速v和牵引阻力Ft的范围，将拖拉机负载特性场(vn，Ftn)离散化，同时将HMCVT工作点变量泵排量比en和行星排行星比kn离散化，n为整数；

2)当目标车速v和牵引阻力Ft取初始最小值v1和Ft1时，通过式(5)～(7)求解出所对应的发动机转速ne1、转矩Te1。

式中ib为变速器的变速比；μ为地面摩擦系数；m为拖拉机的质量，kg；g为重力加速度，9.8 N/kg；rq为驱动轮半径，m。

3)通过式(2)计算出车速为v1时的发动机有效燃油消耗ge1，再结合式(3)计算出此时HMCVT的传动效率ηb1，进而求得ge1/ηb1的比值；在式(4)的目标函数中依次循环带入HMCVT变量泵排量比e1～en和行星排行星比k1～kn，取计算结果中的最小值，并记录此时发动机转速、转矩、HMCVT变量泵排量比和行星排行星比值。

4)循环带入牵引阻力Ft2～Ftn并重复步骤1)～3)，确定车速v1下所有拖拉机工作点的最佳发动机转速、最佳发动机转矩、HMCVT最佳变量泵排量比和最佳行星排行星比。

5)循环带入目标车速v2～vn并重复步骤1)～3)，确定在整个负载特性场下所有拖拉机工作点的最佳发动机转速、最佳发动机转矩、HMCVT最佳变量泵排量比和最佳行星排行星比。

根据以上步骤通过一次优化选出所有参数的最佳区域，再结合拖拉机经济性实际控制过程，对照不同目标车速和牵引阻力调节各个参数，实现拖拉机经济性最佳。

3 结果与分析

以中小型(功率≤50 kW)拖拉机为对象，搭载图1所示HMCVT，动力源选择BM58G型柴油发动机。拖拉机牵引阻力为10 kN，行驶速度0～15.01 km/h。拖拉机设计参数见文献[31]。

3.1 发动机和HMCVT的最佳工作点求解结果

结合Matlab软件，使用参数循环算法，对控制参数发动机转速ne、转矩Te和HMCVT变量泵排量比e和行星排行星比k进行优化，优化过程总时长为1 942.839 s，拖拉机经济性最佳时的控制参数求算结果如图3所示，由图3可知，在负载特性场内任意牵引阻力和目标车速下均有唯一的最佳转速、转矩、排量比和行星比。由图3a可知，最佳变量泵排量比范围为-0.4～0.2之间，且呈阶梯状分布，排量比为0的平台部分表示此时HMCVT工作在纯机械传动状态。由图3b可知，在任意负载和车速下，最佳行星排行星比区间为1.65～1.95，当排量比为0时，HMCVT的工作状态为纯机械传动，传动较为平稳，且传动效率达到最高，为0.97。由图3c可知，发动机最佳转矩区间为210～275 N·m，当拖拉机工作在牵引阻力较小工况时，较小的发动机转矩就能保证拖拉机在低速作业下获得较低的燃油消耗。当牵引阻力增加时，发动机需要提供更大的输出转矩以保证拖拉机有较大的牵引力，若牵引阻力和车速持续增大，超过发动机极限，将导致发动机熄火。由图3d可知，发动机最佳转速区间为1 015～2 399 r/min，结合发动机有效燃油消耗率特性曲线可知，发动机在此区间的燃油消耗较低，为222～269 g/(kW·h)，符合发动机工作特性。

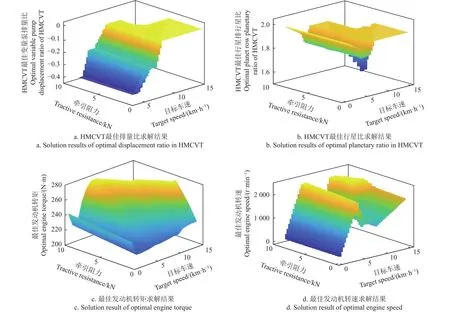
图3 拖拉机最佳经济性控制参数求解结果Fig.3 Solution results of optimal economic control parameters of tractor

根据图3所示的计算结果，再结合图2所示的控制流程，针对负载特性场内的任意实际工作点，查取图3中所有控制参数的相应唯一值，再调节发动机转速ne、转矩Te和HMCVT变量泵排量比e、行星排行星比k至对应位置，即可实现拖拉机经济性最佳的实时调节。

图4为最佳控制参数下的拖拉机整车比油耗情况，由图4可知，整车最低燃油消耗为245.496 g/(kW·h)，较中小型拖拉机燃油经济性评价标准(≤350 g/(kW·h))降低了29.86%。

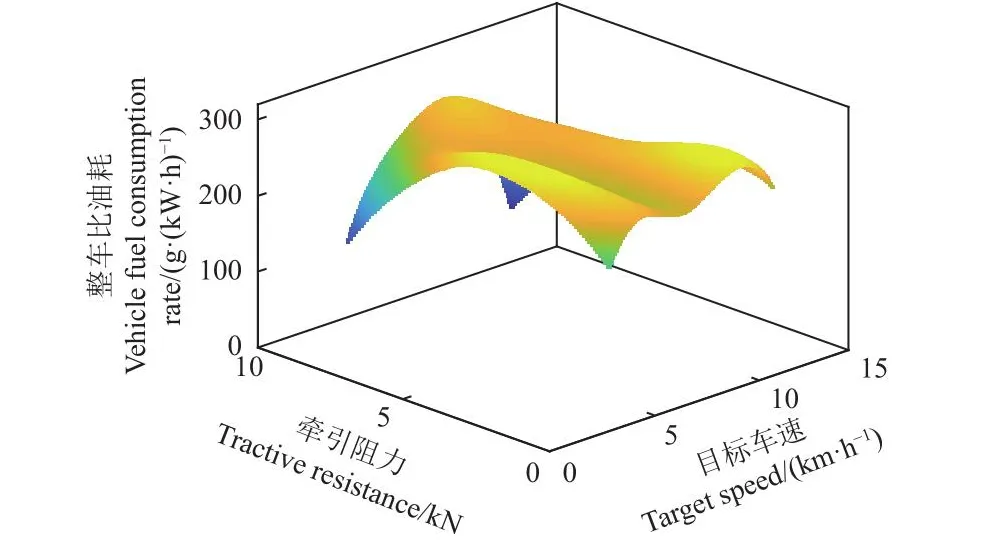
图4 最佳控制参数下拖拉机的比油耗Fig.4 Specific fuel consumption of tractor under the optimal control parameters

3.2 不同工况下行星比对整机经济性的影响

由优化结果可知，行星比的加入使得拖拉机整机燃油消耗有所降低。拖拉机整机燃油消耗随负载的变化而变化，而拖拉机负载取决于不同的作业项目。因此，针对拖拉机不同作业项目，分析加入的行星比对整机经济性的影响关系。

拖拉机的作业速度取决于拖拉机作业项目，常见的作业项目为犁耕、旋耕等，不同作业项目适宜的作业速度如表1所示[32]。

表1 拖拉机适宜作业速度Table 1 Tractor suitable operating speed

为了方便且更为直观的表征行星比对整车燃油消耗率的影响关系，将拖拉机作业工况分为低速工况(移栽、开沟、旋耕)，中速工况(播种、水田犁耕)，高速工况(旱地犁耕、耙地)。

图5给出了不同工况下排量比分别为-0.4，-0.2，0时，整车比油耗随行星比的变化曲线。由图5可知，当排量比为-0.4、-0.2和0时，整车比油耗随行星比的增加而减少，由此可知，当整车需要获得更低的燃油消耗时，行星比在一定范围内越大越好。从车速来看，当排量比一定，拖拉机车速在13 km/h时的燃油消耗均较低，表明拖拉机能进行犁耕等负荷较大的作业项目，且能保证负载在一定范围内波动时拖拉机作业的稳定性。同时，由图5可知，车速越高，整车比油耗越低；从排量比来看，排量比对于对应作业车速下的燃油消耗影响并不明显。在4 km/h的低速作业工况时，排量比为-0.4、-0.2和0时的比油耗均处于288 g/(kW·h)附近；在7 km/h的中速作业工况时，排量比为-0.4、-0.2和0时的比油耗均处于278 g/(kW·h)附近；在13 km/h的高速作业工况时，排量比为-0.4、-0.2和0时的比油耗均处于255 g/(kW·h)附近。因此，针对不同作业工况，需要调节排量比和行星比到适当区间，以保证整车燃油经济性最佳。

图5 不同排量比 e 下整车比油耗随行星比的变化Fig.5 Variation of vehicle fuel consumption rate with planetary ratio under different displacement ratios e

4 最佳经济性下的无级变速多参数调控效果

为了便于对比整车在不同作业车速下最佳经济性调控效果，验证以ge/ηb最小为目标的拖拉机无级变速控制的燃油经济性，分析多参数调控下的HMCVT传动效率及最佳变速比的分布情况。

4.1 HMCVT实际工作点下的变速比分布

根据优化结果，得到最佳变速比区间，根据经济性最佳时的排量比和行星比可知，最优排量比及最佳行星比区间分别为-0.4～0和1.65～2.0，由此可得经济性最佳时的最佳变速比，如图6所示，为方便计算，将HMCVT的变速比定义为输出转速与输入转速之比。

根据图5可知，低、中、高速3种作业速度工况下，排量比和行星比值取值越大，整车经济性越好。再根据变速器速比特性可知，行星比固定，排量比变化时，对应一系列的变速比，反知，排量比固定，行星比变化时也对应一系列变速比，与传统的变速比仅随排量比变化相比，本文提出的HMCVT系统在一定程度上拓宽了变速器比的范围，从图6中看出当排量比和行星比越大，整车的变速比区域越大。

排量比为0时，图5c行星比变化对整车经济性影响并不大，此时，动力几乎全由机械路径进行传递，液压路径传递的功率可忽略不计。由图6也看出，排量比为0时，变速比达到最佳变速比区域的值最大，为0.38，整车处于稳定的工作状态，由此可知，多参数最佳经济性调节的HMCVT的变速比范围较宽，为0.07～0.38。

4.2 HMCVT实际工作点下的传动效率分布

拖拉机属于一机多用的农业机械，传动效率高效区间要求较大。对于传统HMCVT，对于某一工况下的纯机械传动时的传动效率只有一个值，本文算法加入影响传动效率的行星比k，使得纯机械传动时的传动效率形成一个区间，因此，拖拉机高效传动拥有更多的可能。

针对文中液压机械调速段来说，因为其传动路线相对较长，传动效率以0.92为界划分高、低效率区[12]，图7为低、中、高速作业工况下整车传动效率分布。

图7 HMCVT传动效率分布Fig.7 Transmission efficiency distribution of HMCVT

根据图6可知，对于低、中、高速3种作业工况来说，排量比和行星比越大，整车工作变速比的区域越大，再结合图7可知，此时整车传动效率处在高效率区，效率约为0.92。对于排量比为0的作业工况来说，由图7可知，当变速比为最佳变速比区域的最大值0.38时，整车传动效率也达到最大，传动效率约为0.97。因此，对于低、中、高速3种作业工况时，取较大的排量比和行星比能有效获得较低的燃油消耗率且能保证HMCVT传动系统主要在高效率区工作。

5 结 论

本文进行了基于参数循环算法的拖拉机HMCVT燃油经济性最佳的多参数优化研究，分析了行星比的加入对整机经济性及变速调控效果的影响，得到如下主要结论：

1)提出了拖拉机经济性的影响因素除了发动机转速、转矩、变量泵排量比3个基本参数之外，行星排行星比的加入也对整机经济性有一定影响。

2)提出了以发动机和HMCVT协同控制的多参数调节方式。阐述了拖拉机在任意工况下，调节发动机转速转矩和HMCVT排量比、行星比，控制拖拉机在最佳经济性下工作的控制原理，并采用参数循环法求解出拖拉机整机经济性最佳时的发动机转速转矩和HMCVT排量比、行星比，此时拖拉机燃油消耗率与标准相比降低了29.86%。

3)提出的多参数经济性最佳控制策略易于实时控制，针对拖拉机的作业特点，通过一次优化就可得到的对应参数的最佳区间，对于实际作业工况时，可按照不同工况调节任一参数到相应值，控制较为简单、便捷。

4)通过比较低、中、高不同作业车速下行星比对整机经济性的影响，得到行星比越大，整机经济性越好。从传动效率和变速比两个方面对比了多参数的调控效果，得到一定范围内取较大的排量比和行星比可保证拖拉机工作在速比为0.07～0.38的较宽速比区间和效率不低于0.92的高效率区。

本文研究结果可为无级变速拖拉机变速器开发及应用以及HMCVT的最佳经济性控制策略制定奠定基础。目前研究只处于控制策略的提出阶段，论文仅进行了相关数值模拟计算，尚未进入策略实施阶段，还有待完善拖拉机控制效果的仿真及田间作业验证，其次本方案只是一种传动形式，还有待向多段式的系统及结构上构思，让传动方式有更多的可能。