考虑药罐液体晃动的高地隙喷雾机底盘悬架优化设计

2023-08-08路力权张军昌胡宸玮曹佳宇

农业工程学报 2023年10期

路力权，张军昌，陈军，陈雨，胡宸玮，曹佳宇

（西北农林科技大学机械与电子工程学院，杨凌 712100）

0 引言

高地隙自走式喷雾机具有高效、环保等优势，被广泛应用于农作物喷药与施肥作业[1-3]。随着喷雾机作业速度的提高，离地间隙以及药罐容量的增大，使其必须配备减振效果更佳的悬架系统。目前，主要通过悬架系统的结构改进以及主动控制来提升其减振性能。结构改进方面，陈雨[4]设计了一种带附加气室独立式立轴空气悬架，李中祥等[5]提出了一种气液组合悬架系统；主动控制方面，多采用模糊PID控制方法[6-8]，武秀恒等[9]提出了有限频域主动悬架减振策略，张鹏等[10]提出了直接横摆力矩控制策略。

基于寻优算法的悬架系统参数优化[11-13]是实现悬架主动控制[14-15]的重要前提，而针对高地隙自走式喷雾机悬架开展的研究较少，王麒淦等[16]以喷雾机行驶平顺性为目标，匹配出了最优的悬架参数。同时，喷雾机运行工况复杂，转场运输时，较快的行驶速度要求喷雾机悬架能够充分耗散地面传递至车身的振动能量，保证舒适平顺；喷药作业时，需兼顾地面友好性，即不能产生过大的轮胎动载荷，造成土壤的压实与破坏。喷雾机作业时，在复杂路面激励下药罐内药液的晃动冲击作用导致整车侧倾、俯仰运动加剧，喷药过程中充液条件的变化导致的整车簧载质量以及质心高度的改变[17]，使得悬架系统难以在其最佳匹配参数条件下工作，极大的影响了整机行驶平顺性与施药效果。而药罐内液体晃动呈现较强非线性，通过控制方程进行线性化描述时，自由液面难以得知[18]。液体晃动作用于喷雾机罐体内壁的力及力矩，虽可通过Galerkin原理离散化求解，但仍旧存在一定误差[19]。目前多采用等效模型法来分析充液系统动力学问题[20-26]。然而，围绕高地隙喷雾机开展的整机动力学及悬架系统的研究大多忽略了液体因素的影响，导致分析结果出现较大误差。

本研究采用等效力学模型法研究罐内液体晃动力学特性，在考虑罐内液体因素的前提下，建立喷雾机垂向动力学模型，并对悬架系统进行优化，获取喷雾机不同充液条件及作业工况下的悬架最优刚度、阻尼组合参数。最后利用课题组研发的小型喷雾机进行整车试验，验证悬架参数优化效果。拟为喷雾机悬架系统进一步优化与控制提供实施手段与理论基础，提高整机行驶平顺性及作业质量。

1 喷雾机垂向动力学模型

1.1 液体晃动等效模型建立

高地隙喷雾机罐内药液在路面激励作用下受迫晃动冲击药罐壁面，产生变化的动态负载，致使作用于车身的倾覆力矩增加，极大地降低了整机稳定性。因此，在建立喷雾机整机动力学模型时考虑罐内液体因素十分必要。本文采用等效力学模型法，构建“弹簧-质量-阻尼”力学系统来描述罐内液体往复冲击的非线性运动。如图1a所示，建立罐内液体晃动坐标系。取药罐底面中心为坐标原点O，x为喷雾机前进方向，z为垂直方向。根据连续性方程与不可渗透条件[27]，罐内液体晃动满足式(1)。

图1 罐内液体晃动模型建立Fig.1 Modeling of liquid swaying in the tank

式中Φ(x,y,z,t)为势函数；h(x,y,t)为波高函数；Ω为罐体内流体域；τ为液体自由液面；υ为罐壁湿表面。

建立罐内液体横向晃动等效力学模型如图1b所示，模型由固定质量块，移动质量块，阻尼及刚度弹簧构成。设罐体受到沿y轴的激励为(t)时，mc1偏离平衡位置的位移为xc1，则一阶等效质量块运动微分方程可表示为

根据系统动力学理论[28]，等效模型在水平方向上产生的力Fe与力矩Mce如式（3）和（4）所示。

式中ω1为罐内液体一阶晃动自然频率，Hz。

根据力学相似原则，罐内实际液体冲击产生的力和力矩与等效模型产生的力和力矩相等，可求得横向晃动等效模型各参数。同时，罐内液体的横向与纵向晃动分别对整车行驶的侧倾与俯仰运动产生了影响，因此，依据横向等效模型，同理建立纵向液体晃动弹簧-质量-阻尼等效力学模型，根据等效准则与相似原理，求得液体纵向晃动等效模型各参数。根据本团队初步研发的喷雾机搭载的液罐长为1 m，底面直径为0.6 m，求解得到各充液比下横向、纵向等效模型参数值如表1所示。

表1 等效模型各参数Table 1 Parameters of Horizontal Equivalent Model

1.2 整机垂向动力学模型建立

融合液体晃动等效力学模型，建立喷雾机整车7自由度垂向动力学模型。由于喷雾机车身结构特殊，运行工况复杂，故作出如下假设[3]：1）液罐与车身之间无缓冲机构，视为刚性连接；2）车身侧倾、俯仰运动中心与液罐底部中心重合，且罐内液体晃动时以倾覆力与力矩的形式作用于车身之上；3）将喷杆质量视作簧载质量的一部分，忽略其晃动作用的影响。

以“地面-轮胎-悬架-车身-罐体”构成的系统为对象，构建如图2所示模型。

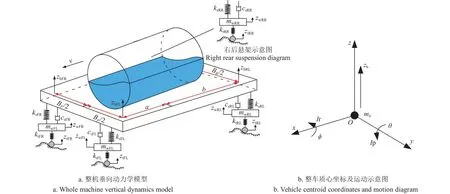
图2 整机模型示意图Fig.2 Schematic diagram of whole machine model

当车身俯仰角θ与侧倾角φ较小时，车身FL、FR、RR、RL簧载质量的垂向位移可近似表达为如式（5）～（8）所示。

综合液体晃动等效力学模型，并结合牛顿第二定律，得到车身质心处的垂向振动、车身俯仰运动、车身侧倾运动及非簧载质量的垂向振动微分方程为分别如式（9）～（12）所示。

式（10）~（12）中，Mf、Mc分别为液体纵向、横向晃动力矩，N·m

2 喷雾机悬架参数优化

2.1 Simulink仿真模型建立

基于罐内液体晃动等效力学模型与喷雾机整车动力学模型，在Matalb/Simulink中搭建仿真优化平台。建立的仿真平台以四轮随机路面激励作为输入信号，以四轮动载荷、车身垂向加速度、侧倾角速度、俯仰角速度为输出信号。整机基本参数根据团队研发的喷雾机实测如表2所示，其中车身转动惯量根据所绘制喷雾机Solidwork三维模型质量属性分析模块计算获得。

表2 喷雾机基本参数Table 2 Basic parameters of sprayer

2.2 优化方法与目标

喷雾机车身质心较高，在行驶过程中路面激励复杂，且罐内液体受迫晃动产生的冲击作用，都对其运行平稳性与舒适性产生了较大影响。因此，在改进车身结构的同时，获得并采用最佳的悬架参数组合也是提高喷雾机行驶稳定性与舒适性的重要方法。本研究采用遗传算法（Genetic Algotithm）对前后悬架刚度、阻尼参数，即对K=[cs1,ks1,cs2,ks2]4个变量参数进行优化[29]。运用Matlab/Optimization中的GA工具进行算法求解，通过Sim函数实现对Simulink动力学仿真模型的运行及仿真结果的调用。优化步骤如图3所示。

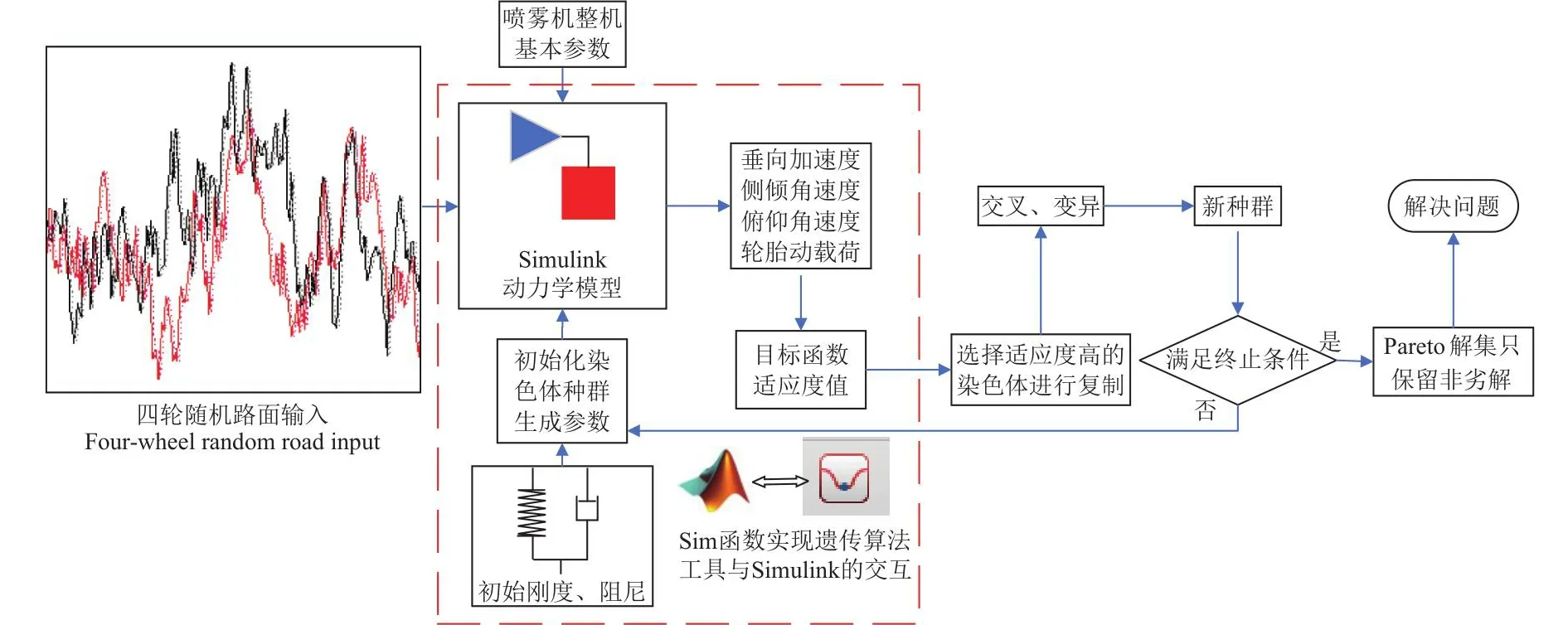
图3 遗传算法优化步骤Fig.3 Genetic algorithm optimization steps

喷雾机的运行工况可分为转场运输与喷药作业两种。在转场运输过程中，行驶路面大多为非田间路面，其行驶速度相较于喷药作业更高。因此，在此运行工况下，需将提高车辆行驶平顺性，减缓车身俯仰与侧倾运动作为优化的主要目标。而喷雾机在进行喷药作业时，行驶路面为田间路面。此时，来自路面的外部激励更加强烈，提高喷雾机的行驶稳定性以保证施药效果的同时，应通过对悬架参数的优化，降低动态载荷以减缓轮胎对土壤的压实作用，保护土壤不被破坏。此外，喷雾机喷药作业时，随着药罐内药液质量的减小，导致作用力矩减小，车身质心降低，此时前后悬架的最佳参数也应发生变化，而这一变化是非线性的，难以推导出药液质量与悬架参数之间的实时变化关系。基于此，本文采用离散方法，即以10%为变化步长，分别得到充液条件为10%～90%时的悬架最优参数矩阵，以保证在不同充液条件下的整车行驶处于最佳状态。

2.3 优化参数设置

2.3.1 目标函数

针对两种喷雾机运行工况，分别建立优化目标函数。当喷雾机进行转场运输时，在满足轮胎载荷的基本要求下，应通过减小垂向加速度、侧倾加速度、俯仰角速度以提高整机平顺性。同时，满足归一性与非负性的前提下根据层次分析法分别赋予以上3个变量权重系数，构建目标函数如式(13)所示。

式中w1、w2、w3分别为垂向加速度、俯仰角速度及侧倾角速度的权重系数；为垂向加速度初始参数下的输出结果，m·s2；、分别为俯仰角速度与侧倾角速度初始参数下的输出结果，rad·s; rms表示各个输出结果的均方根。

当喷雾机进行喷药作业时，在提升整机行驶平顺性的同时应降低轮胎载荷以减少对土壤的破坏[30]。构建目标函数如式(14)所示。

式中w4、w5、w6、w7分别为垂向加速度、俯仰角速度、侧倾角速度及车轮动载荷的权重系数；F为优化条件下的轮胎动载荷输出结果，N；Finitial为初始参数下的轮胎动载荷输出结果，N。

式(13)、(14)中的权重系数满足归一性与非负性的前提下根据层次分析法[31]，即喷雾机转场运输工况下优化目标为提高车辆行驶平顺性，而平顺性评价指标中则以车身垂向加速度为主，因此，赋予车身垂向加速度更大权重。喷雾机喷药作业时则考虑平顺性的同时以提高道路友好性为主，因此赋予轮胎动载荷更大权重。据此，令w1=0.4，w2=w3=0.3，w4=w5=w6=0.2，w7=0.4。

2.3.2 约束条件

喷雾机前、后偏频是影响整车行驶平顺性的主要原因之一。根据悬架设计要求，后悬架偏频一般大于前悬架偏频。同时，根据车辆类型的不同，悬架偏频的选取亦不同，其规律满足轿车、客车及货车的偏频选取依次增大，其一般满足0.9～2.2 Hz[32]。根据喷雾机自走式的运行方式，结构特殊及运行工况复杂的特点，比对其他类型车辆，选择前、后悬架的偏频fn1、fn2的范围分别满足式(15)与式(16)。

式中kf、kr为前、后悬架刚度，N/m。

根据车辆悬架系统小阻尼设计要求，前后悬架阻尼比ξf、ξr应满足

式中cf、cr为前、后悬架阻尼，N·m/s；m为车身簧载质量，kg。

根据式(15)～(18)可得到前、后悬架不同充液条件下的刚度与阻尼范围，取其中间值为优化初始值。

喷雾机进行喷药作业时，由于考虑对土壤的保护，车轮动载荷[33]将作为优化的主要目标之一表现在目标函数中。而转场运输时为保证喷雾机行驶的安全性，防止车轮失去附着力，满足车轮跳离地面概率小于0.15%的要求，车轮动载荷σFd与整车重力G的关系应满足

2.4 优化结果及分析

根据喷雾机喷药作业与转场运输的运行工况，设置算法仿真优化的初始激励条件分别车速10 km/h的E级随机路面和D级随机路面。选择遗传算法初始种群规模指数为40，交叉概率为0.8，变异概率为0.05，最大执行代数100代，优化结果如图4所示。以最优参数进行Simulink仿真试验，计算各输出结果的均方根值如表3所示。

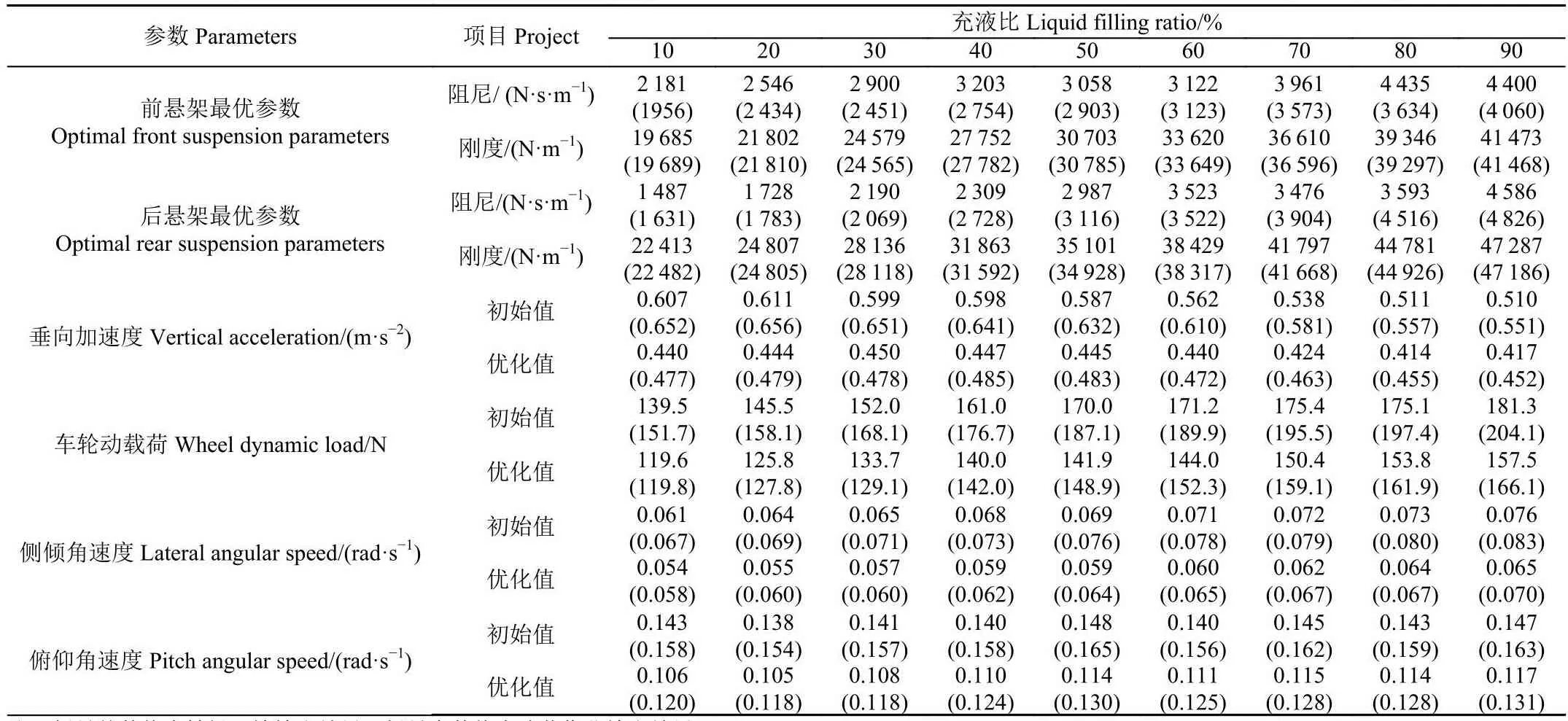
表3 转场运输、喷药作业悬架参数优化及平顺性输出结果Table 3 Output results of suspension parameter optimization and smoothness for transit transportation and spraying operations

图4 悬架参数优化结果Fig.4 Optimization results of suspension parameter

由图4优化结果可以看出前、后悬架的最优参数与仿真设置的初始值存在明显差异。其中，悬架的刚度参数较初始值大幅减小，而悬架阻尼参数则相对初始值略微增大。同时，悬架的最佳刚度、阻尼值都随着充液比的增大以及车身质量的增大而增加。其次，前后悬架的最优参数存在差异，且后悬架刚度始终大于前悬架。这一结果符合悬架设计过程中后悬架刚度通常大于前悬架刚度的设计要求。此外，由于喷雾机喷药作业与转场运输优化时所建立的目标函数不同，对比喷雾机两种工况下的优化结果可以发现，两者阻尼参数存在较大差异，其中前悬架转场运输时的最优值总是大于喷药作业时的最优值，而后悬架的两者最优值则呈现与前悬架相反的规律趋势，而两种工况下的前后悬架刚度最优值则基本一致。

由表3可以看出，以悬架最优参数进行Simulink模型仿真时，其输出量车身垂向加速度、俯仰角速度、侧倾角速度以及车轮动载荷的均方根值均发生了不同程度的降低。此结果表明，在满足悬架设计的基本范围内适当减小悬架的刚度值，增加悬架的阻尼值，且满足一定的前后悬架参数关系的条件下，能够提高整车行驶的平顺性，降低车轮动载荷，减小喷雾机作业时对农田土壤的破坏。

以充液比为50%时为例，Simulink各输出量时域对比结果如图5、图6所示。

图5 喷雾机喷药作业优化结果对比Fig.5 Optimization results comparison of sprayer spraying operation

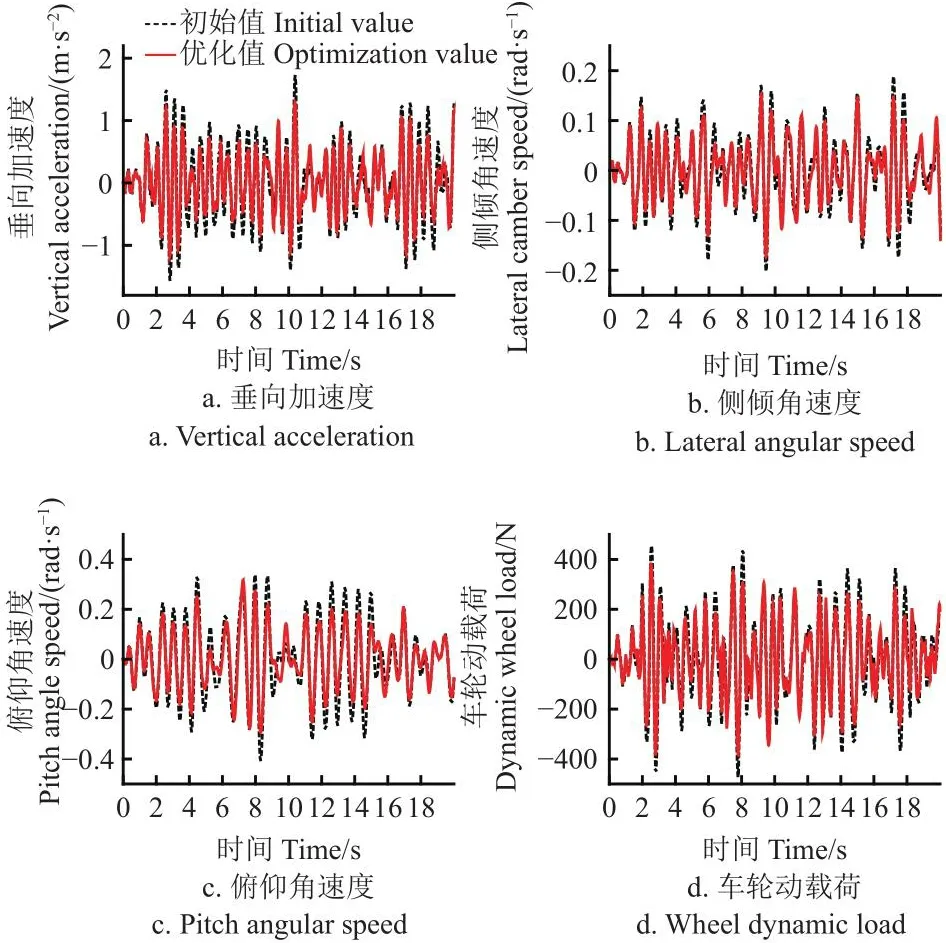
图6 喷雾机转场运输优化结果对比Fig.6 Comparison of optimization results of sprayer transition transportation

分析图5、6可知，优化之后的各参数时域结果与初始状态下的输出结果在响应频率上基本保持一致，而响应幅值发生了显著降低。此结果说明了通过优化悬架参数而提高喷雾机行驶平顺性以及降级轮胎载荷、土壤破坏的有效性。

针对喷雾机转场运输与喷药作业时，对不同作业指标的优化百分比如图7所示。由图7可以看出，车身垂向加速度、侧倾角速度、俯仰角速度及车轮动载荷最大可降低27.5%、16.4%、25.8%以及17.6%。同时，不同充液条件下的优化效果存在一定差异。分析对比可知，车身垂向加速度与俯仰角速度随着充液比的增大，其降低量逐渐减小，而车轮动载荷、侧倾角速度的最佳优化效果分别出现在充液比为50%和60%时。此外，喷雾机两种运行工况下的优化效果也不同，对比转场运输工况，喷药作业时车轮动载荷的减小量更大，而其他三组变量的优化结果则多为转场时的效果更佳。这一结果符合本文在优化之初所建立的优化目标，对于喷雾机转场运输的优化着重于提高整车平顺性，而对喷药作业，在兼顾平顺性的同时应当降级其车轮动载荷以减少整机对土壤的破坏。

图7 各充液条件下的优化效果对比Fig.7 Comparison of optimization effects under various liquidfilled conditions

3 整机试验

3.1 试验目的与方法

利用课题组研发的小型喷雾机平台进行整车试验，以验证悬架参数多目标优化的有效性。试验采用加速度传感器、角度传感器等测量装置，选取典型工况进行。将悬架优化前后参数条件下测得的车身加速度、各悬架簧载/非簧载质量加速度、车身俯仰/侧倾角速度等整机平顺性响应结果，进行对比分析。试验时间为2023年2月，试验地点为陕西省咸阳市熠泽智能农业科技发展有限公司小麦试验田。结合试验目的及悬架优化仿真试验条件，设置两组变量为喷雾机作业路面条件和底盘悬架参数，进行4次重复试验，如表4所示。

表4 试验分组与条件Table 4 Experimental grouping and conditions

为测得喷雾机簧载/非簧载质量垂向加速度，将多个PCB356A15型加速度传感器固定于车轮与转向轴固定平台处以及悬架顶端与车架连接平台处。同时，固定于车架上的加速度传感器也可测得喷雾机车身垂向加速度。为测得车身俯仰/侧倾角速度，将BWT901CL型角速度传感器固定于整机质心处（图8）。

图8 喷雾机试验平台与传感器安装Fig.8 Sprayer test platform and sensor installation

3.2 试验结果及分析

根据喷雾机运行与负载能力，选择在充液比为30%，车速为8 km/h的条件下进行。试验过程中喷雾机需经历起步加速、稳定行驶以及减速停止3个阶段，为提高试验准确性，截取稳定行驶阶段的60 s数据结果进行分析。其中，加速度传感器采样频率为1 kHz，倾角传感器采样频率为20 Hz，而本研究涉及药液晃动的悬架振动主要为低频振动，因此对加速度传感器采样信号进行截止频率为20 Hz的低通滤波处理，以试验1非簧载质量加速度采样为例，处理结果如图9所示。

图9 20 Hz低通滤波结果示意图Fig.9 Schematic diagram of 20 Hz low-pass filtering results

由图9a可知，加速度传感器采样结果频率构成复杂，高频信号成分较多，对实际结果影响较大，而由图9b可知，经过滤波处理，采样结果幅值显著减小，这一结果说明了滤波处理的必要性。据此，对各试验组加速度传感器采样结果分别进行滤波处理。

对各试验组簧载/非簧载质量加速度响应结果进行滤波处理，统计获得均方根值，如表5所示。由表5可知，簧载质量垂向加速度值远小于非簧载质量加速度，说明了悬架减振效果良好。试验3、4的测量结果均方根值均大于1、2组测量值，前两组试验条件为非田间路面而后两组为田间路面，因此，这一结果符合田间路面振动响应数值更大的实际情况，具有合理性。试验2、4的减少量均大于试验1、3的减小量，由于2、4是将悬架调节为最优参数下的试验结果，因此，调整后的悬架具备更好的减振效果则进一步说明了悬架优化的有效性。

表5 各试验组加速度均方根值Table 5 Root mean square (RMS) values of acceleration for each test group

喷雾机车身垂向加速度响应对比结果如图10所示。分析图10可知，调整悬架为最优参数的试验2、4的车身垂向加速度小于悬架为初始参数的试验1、3，在两种车轮运行路面下，悬架参数的调整分别使其车身垂向加速度降低了15.58%与18.72%。其中，田间试验结果降低量均在20%以下，小于图7仿真试验结果。这是由于在仿真试验中对整车建模进行了一定简化，忽略了喷杆晃动、电机转动、结构件振动等对整车产生影响。此外，对比试验结果与仿真结果可知，该试验所测得的数据与悬架参数优化仿真试验所得结果较为接近，这一现象说明了本试验的合理性与准确性。

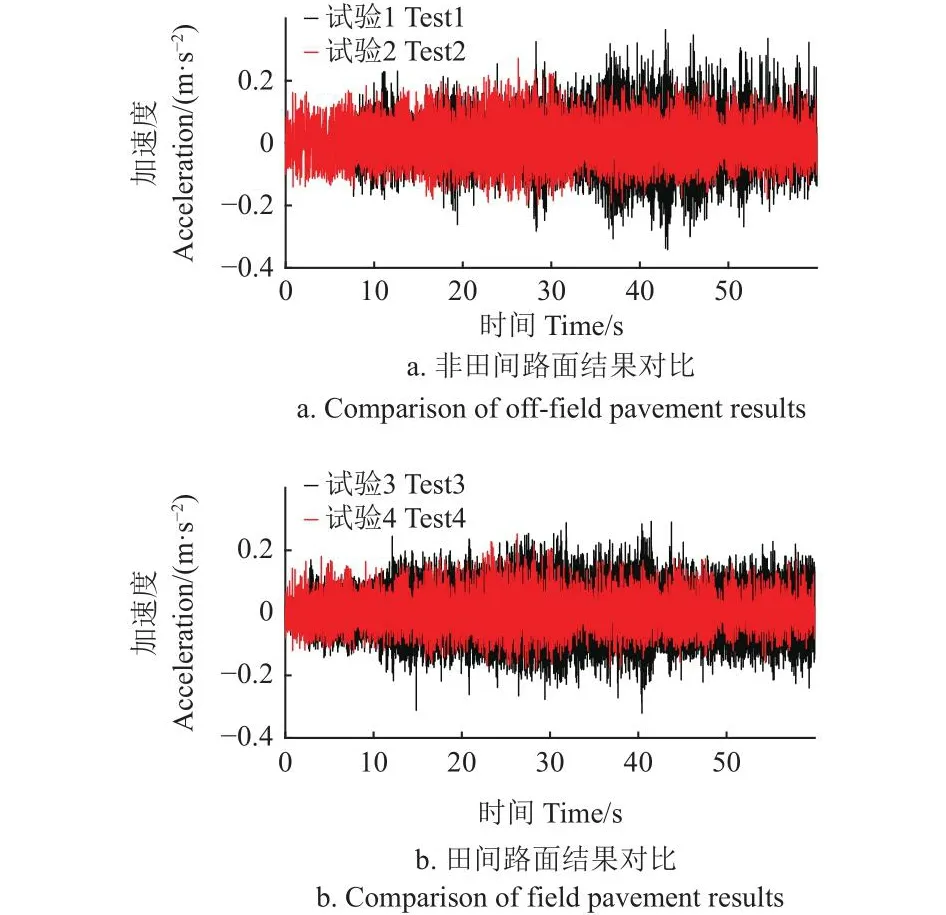
图10 喷雾机车身垂向加速度响应结果Fig.10 Response results of vertical acceleration of sprayer body

车身侧倾角速度、俯仰角速度是评价车辆行驶平顺性的重要指标，截取试验20～30 s响应对比结果如图11所示。

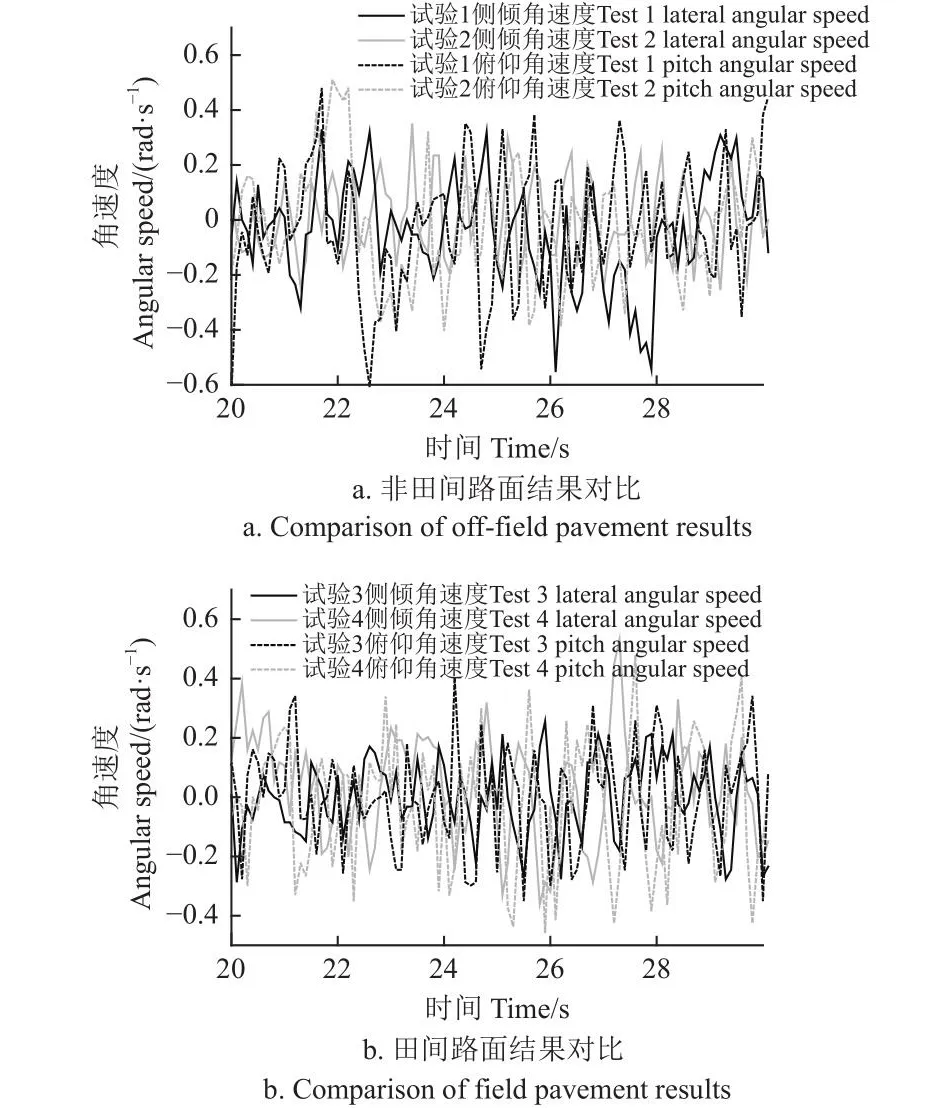
图11 喷雾机车身侧倾角速度响应结果Fig.11 Roll angle speed response results of sprayer body

由图11可以看出，悬架调整为最优参数后的车身侧倾/俯仰角速度试验结果均小于初始参数下的测量值，这一结果可进一步说明悬架参数优化的有效性。分析图中数据可得，悬架参数的优化对于车身侧倾/俯仰角速度的降低均在10%以上，说明悬架优化效果良好。分析对比图中各曲线，车身侧倾角速度的结果均小于俯仰角速度，造成这一结果的原因是所设计加工的小型喷雾机前后轴距略大于左右轮距，因此产生了车身的俯仰运动相较于侧倾运动更为剧烈的现象。此外，对比试验结果与仿真结果可知，试验所得的车身运动响应结果略大于仿真结果，这是由于仿真试验中对整车的建模进行了一定的简化，忽略了喷杆等作用，而在实际试验中喷杆的振动也会影响整车的运动，改变整车的质心位置，从而使得车身侧倾/俯仰角速度增大，这一结果符合实际情况。