气吸式播种机多分支汇流管路气压损失分析与试验

秦 伟 ，王在满 ，王钰静 ，钱 诚 ，何思禹 ，张明华 ，臧 英 ※

（1.华南农业大学工程学院/岭南现代农业科学与技术广东省实验室，广州 510642；2.广东省农业人工智能重点实验室，广州 510642；3.华南农业大学南方农业机械与装备关键技术教育部重点实验室， 广州 510642；4.华南农业大学黄埔创新研究院，广州 510715；5.岭南现代农业科学与技术广东省实验室茂名分中心，茂名 525000）

0 引 言

气吸式播种机具有播种精度高、对种子尺寸适应性强和伤种率低等优点，广泛应用于水稻[1-2]、玉米[3]、油菜[4]等作物的规模化种植。排种器作为气吸式播种机的核心部件，其作业质量影响整机工作性能[5-6]；而播种机气力系统稳定的气压供给和调控是排种器适应多种作物种植和稳定作业的必要保障。

气力系统主要由风机与多分支汇流管路组成，风机为整机作业提供气源，多分支汇流管路则将多个排种器产生的负压支流汇为总流，并输送至风机，实现播种机一机多行协同作业。当前，低能耗、高效率是气吸式播种机的设计目标之一，随着气吸式排种器工作性能的日趋完善[7-9]，其机械结构已不再是气力系统能量损耗的主要原因。由于多分支管路三通处的气流更易相互掺混，并伴随复杂的能量转换[10-11]；管路结构的合理性成为减少气力系统能量损耗的关键。因此，研究多分支汇流管路的气流压力损失，揭示管路汇流过程中的流体运动状态，对设计低损高效的管路结构至关重要。

目前，研究人员为降低多分支汇流管路的压力损失，从结构优化的角度进行了探究[12-14]。ŁUKASZ等分析了Z型与U型汇流管路在支管数量、长度和集管直径等因素影响下的流体压力损失，确定了减小压损的几何结构类型[15]。CHEN等探究了矩形、锥形、抛物线形和椭圆形集管对电子元器件冷却流体分布的影响，指出将矩形集管几何形状优化为其余形状在降低微通道集管压力损失方面具有良好的效果[16]。刘海对小白菜精量复式播种机气力系统负压管路串并联结构进行设计和参数分析，结合排种器的结构特征和标准管道尺寸确定了气力系统负压管路的管道直径为20 mm[17]。师艳平分析了三通管形状、集管直径、液化天然气流量等对多分支管路汇流系统内流动阻力的影响，并通过优化管路几何结构提高了管路系统的输送效率[18]。

综上可知，多分支汇流管路几何结构是影响管路气流压力损失的重要因素，尽管已经取得了一定研究进展，但尚不明确管路几何结构与流体压力损失之间的关联特性，也未有相关的数学模型对具有连续三通结构的多分支汇流管路的压力损失进行预测。尤其在气力式播种机设计过程中，尚未有相对普遍适用的管道选型经验公式对初始管路的参数设计进行统一指导。为此本文以气吸式水稻精量直播机多分支汇流管路结构为基础，通过单因素试验探究多分支汇流管路在不同因素影响下的总体气流压力损失变化，借助Fluent[19]数值模拟手段从微观角度分析多分支管路气流汇聚机理，通过量纲分析方法[20-25]总结管路总体压力损失的定量指标评价模型，以期为气吸式播种机多分支汇流管路的设计选型、结构优化提供参考。

1 整机结构与工作原理

播种机构试验台架如图1所示，主要由机架、风机、排种器、驱动电机、多分支汇流管路及多分支分流管路等组成。多分支汇流管路结构如图2所示，主要由风机、皮托管、负压进风管、出口支管、集管以及入口支管等组成，其中出口支管位于集管中间位置，各入口支管以出口支管为中心，沿集管两侧等距对称分布。试验时，气流通过各入口支管进入集管，而后在集管汇聚并输送至出口支管，完成输送过程。多分支汇流管路的初始尺寸参照水稻种植农艺及2Z-6A气力式水稻精量穴直播机设计参数确定[26]，即入口支管长度150 mm，入口支管内径34 mm；集管内径57 mm，集管封闭端长度100 mm；出口支管长度为200 mm，出口支管内径42.6 mm。

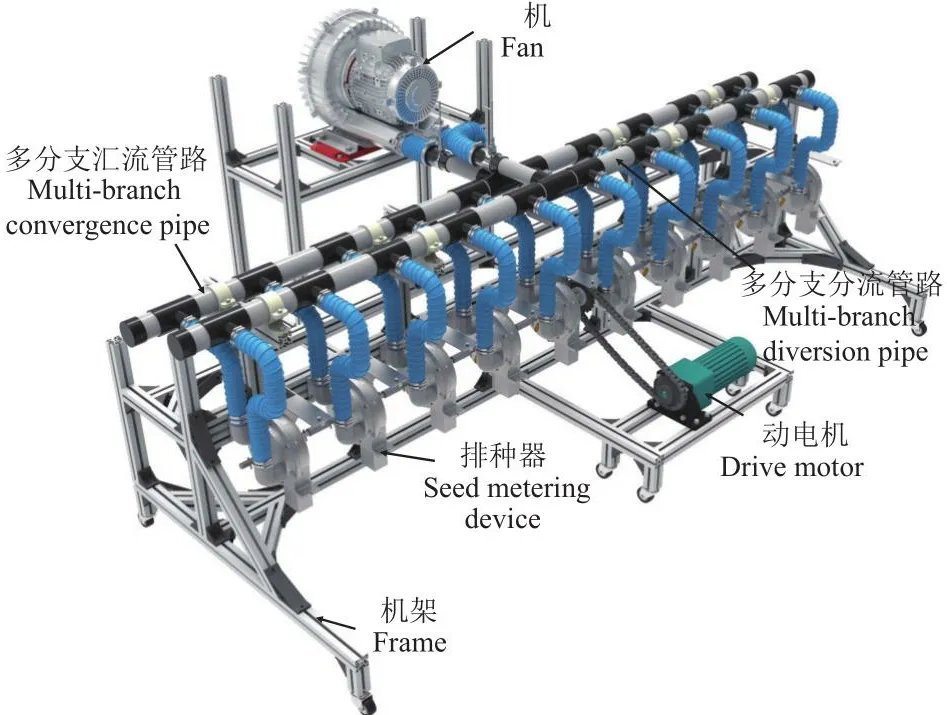
图1 播种机构试验台架Fig.1 Test bench for seeding mechanism

图2 多分支汇流管路Fig.2 Multi-branch convergence pipe

2 试验方法

本文采用单因素试验、数值模拟与全尺寸模型试验相结合的方法开展多分支汇流管路气压损失的研究。首先基于多分支汇流管路模型建立笛卡尔坐标系，确定影响管路内气流流动的试验因素；其次开展单因素试验设计，结合已知的试验因素，在宏观尺度获取多分支管路总流压降、支流流速等气流参数，同时确定试验因素的显著性水平；然后根据单因素试验结果利用Fluent软件从微观尺度探究试验因素对多分支汇流管路内气压损失、气流分配的影响机理；最后通过全尺寸模型试验，利用量纲分析法，构建多分支汇流管路几何结构与管路总体气流压力损失的经验公式。

2.1 试验因素

为确定影响多分支汇流管路总流压力损失的试验因素，以入口支管1的气流监测点（监测点位于多分支汇流管路各入口支管、出口支管内径的中心点）为原点，垂直于气流入口方向为x轴正方向，气流入口方向为y轴正方向，同时考虑到多分支汇流管路两侧支管对称的结构特征，以左侧支管为基础建立笛卡尔坐标系，如图3所示，入口支管监测点1～5处的横坐标xi与入口支管间距δ有关：

图3 多分支汇流管路结构参数与坐标系Fig.3 Structure parameters and coordinate system of multi-branch convergence pipe geometry

式中i为气流入口支管监测点编号，i=1,2,3,4,5。

纵坐标yi均为0；出口支管监测点N的坐标 (x0,y0)取决于入口支管间距δ、入口支管长度l、集管内径γ与出口支管长度Δ等：

■

根据文献[27-28]，入口支管内径d和出口支管内径D也是影响管路总流气压损失的主要参数。因此，本文选取入口支管内径d、入口支管间距δ、入口支管长度l、集管内径γ、出口支管内径D与出口支管长度Δ为试验因素。

2.2 试验设计

试验设计前，对多分支汇流管路内流动的气流做出如下假设：1）结合前期试验确定的管路气流最大马赫数为0.027<0.3[29]，因此管路气体可视为不可压缩流体，且密度不会随压力的变化而变化；2）忽略气体质量，结合前期试验，测定管路进出口气流温度差范围小于0.1℃，因此假设气流在管路内做等温流动；由于国内双季稻低适宜区的暖月平均气温为21.3～28.1℃[30-31]，因此本文将外界环境温度调控为25℃；3）假设管路进出口监测点所测得的气压、气体流速等均为数据的平均值[27-28]；4）由于管路固定于机架，因此忽略管路厚度及因气流冲击而引起的管路自身振动对试验结果的影响。基于上述假设和流体力学理论，得到管内流体的质量连续性守恒方程为

动量连续性守恒方程为

式中u、v、w分别为多分支汇流管路内任一气流微团在x、y、z坐标轴方向的速度分量，m/s；p为各向同性压力，N；ρ为流体密度，kg/m3；μeff为流体有效黏度，与流体动力黏度μ有关，Pa·s；Su、Sv、Sw为动量守恒方程的广义源项，当质量力仅考虑重力时，Sw=-μg，N。

由式（3）～（4）可知，ρ、μ、u，v，w也是影响出口支管压力损失的因素，因此ρ、μ及入口支管1的入口流速V也是影响压力损失的因素。

2.2.1 单因素试验设计

将多分支汇流管路总体气压损失ΔP作为衡量管路性能的定量评价指标，结合前文分析，选取ρ、μ、V、d、l、δ、γ、Δ、D作为影响ΔP的试验因素。依据前文假设，忽略ρ及μ的影响；由于入口支管1的入口气流流动趋势并不独立依赖d与V，为了综合考虑d与V的影响，选取二者的关联物理量流量Q作为试验因素。最终确定Q、d、l、δ、γ、Δ、D作为影响多分支汇流管路压力损失的试验因素。

以多分支汇流管路的初始尺寸为0水平点，结合商用PVC管路的标准结构参数确定各因素水平值，选取距离出口支管最远端的入口支管1的入口流量Q作为试验因素的标准依据，根据前期试验[26]确定Q的中间水平值为0.002 7 m3/s，以0.000 9 m3/s为变化梯度，单因素试验的因素水平如表1所示。

表1 试验因素水平表Table 1 Experimental factors and levels

采用商用PVC管路、PVC三通结构和PVC管粘合剂等对多分支汇流管路的集管与支管进行连接。选用皮托管[32]及LR-SG312S11L13型数字式风速风压测量仪测量出口支管负压值，选用AS816型风速仪测量入口支管1气体流量。每组试验开展5次，试验结果取平均值。

2.2.2 仿真试验设计

结合单因素试验结果，利用Fluent仿真软件进行多分支汇流管路气流流动趋势的数值模拟。采用Realizablek-ε湍流模型[27-28]，利用Ansys软件Geometry模块对多分支管路进行三维几何建模。为减少计算量，忽略集管与支管三通连接处的不连续性，利用Mesh模块对进行网格划分，各因素水平下的网格数量如表2所示。在多分支管路气流汇聚过程中，剧烈变化的压力梯度会造成边界层分离，因此在近壁面采用增强壁面，压力和速度的空间离散和耦合求解采用SIMPLE算法，方程离散化迭代处理均采用二阶迎风格式，各迭代变量的收敛残差均设定为10-4，迭代步数为1 000步，压力基求解，稳态计算。为便于仿真结果的比较，将气流入口边界设置为velocity-inlet，入口支管2～10的入口边界流速由单因素试验结果确定，支管入口气流方向垂直于入口边界平面，入口边界压力与大气压相同，设置为0；气流出口边界设置为pressure-outlet，出口气流方向垂直于出口边界平面，出口边界压力值为单因素试验所测定的压力值。

表2 各因素水平下的网格数量Table 2 Number of meshes at each experimental factors level

2.3 全尺寸模型试验

2.3.1 量纲分析法

气流在多分支汇流管路中的流动是一个复杂过程，多分支汇流管路总体压力损失是管路几何结构与气流流速的综合作用结果，因此建立一个普遍适用的多因素的指标定量预测模型十分必要。与正交试验相比，量纲分析法[20-25]是建立多因素与指标间函数关系的一种相对准确且快速的方法，可将诸多因素与评价指标整理为一个适用范围较为准确的经验公式。本文采用量纲分析法对多分支汇流管路在不同因素影响下的气压损失进行定量评价。结合单因素试验方案及量纲分析Π定理[33]，得到与经验公式有关的11个变量，即ρ、h、μ、Q、d、l、δ、γ、Δ、D、ΔP。选取MLT系统作为量纲分析系统，以质量量纲M、长度量纲L、时间量纲T为基本量纲，其余量纲为导出量纲，得到表3所示的各试验因素及量纲。

表3 试验因素及其量纲Table 3 Experimental factors and their dimensional matrix

在整个试验过程中，ρ、μ、h值是固定的，因此选取ρ、μ、h为参考物理量，以参考量为基础的量纲矩阵系数，如表4所示。

表4 以参考物理量为基础的量纲矩阵系数Table 4 Dimensional matrix coefficients based on reference physical quantities

根据Π定理及表4，推导得到8个Π方程：

将含有ΔP的Π1作为因变项，根据文献[33]可得如下函数关系式：

2.3.2 Π方程的试验设计

此组分方程主要探讨Π2对Π1的影响，由于ρ、μ、h值固定，因此Π3、Π4、Π5、Π6、Π7和Π8值应是固定的，将Q的基值设置为0.000 9 m3/s，并以0.000 9 m3/s为梯度增加至0.004 5 m3/s。

此组分方程主要探讨Π3对Π1的影响，取Π2、Π4、Π5、Π6、Π7和Π8为固定值，结合标准PVC管内径，对应d值分别为19.4、27.2、34.0、42.6和45.2 mm。

此组分方程主要探讨Π4对Π1的影响，由于h为定值，Π4的变化主要通过改变l值实现，设l的基值为100 mm，并以25 mm为梯度增加至200 mm。

此组分方程主要探讨Π5对Π1的影响，由于h为定值，Π5的变化主要通过改变δ值实现，根据水稻种植农艺要求，设δ的基值为200 mm，并以25 mm为梯度增加至300 mm。

此组分方程主要探讨Π6对Π1的影响，由于h值固定，Π6的变化主要通过改变γ值实现，结合标准化PVC管内径，对应的γ值分别为42.6、53.6、57.0、67.8和81.4 mm。

此组分方程主要探讨Π7对Π1的影响，由于h值固定，Π7的变化主要通过改变Δ值实现，设Δ的基值为150 mm，并以25 mm为梯度增加至250 mm。、、和的设计过程与1）、2）相同。

此组分方程主要探讨Π8对Π1的影响，由于h值固定，Π8的变化主要通过改变D值实现；设D的基值为42.6 mm，结合标准化PVC管内径，D值分别为34.0、36.0、42.6、53.6和57.0 mm。

各组Π方程的试验方案如表5所示。

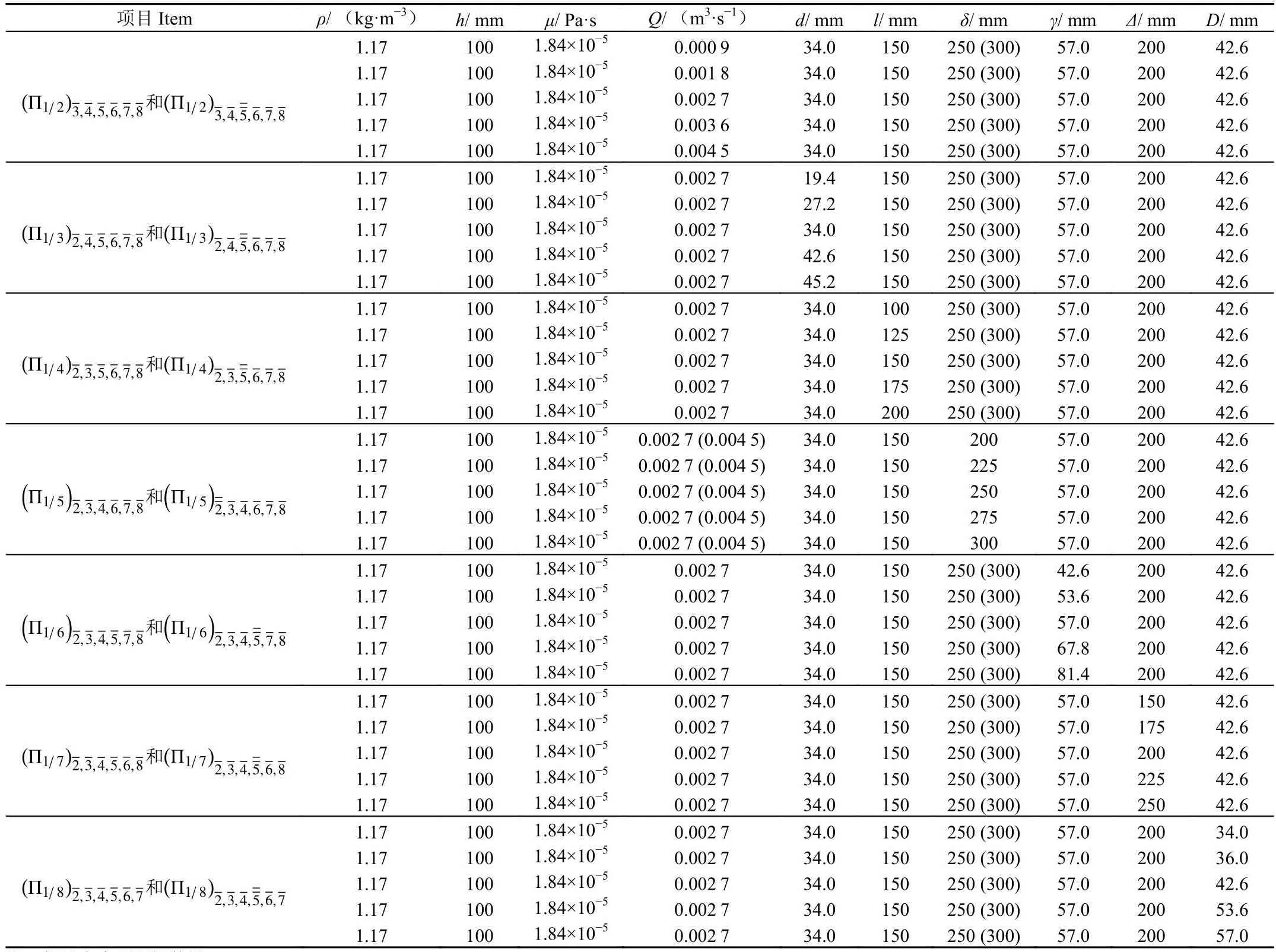
表5 各组Π方程的试验设计Table 5 Experimental design of each Π equations

3 结果与分析

3.1 单因素及仿真试验结果与分析

结合单因素试验结果，利用Fluent软件CFD-Post后处理模块对仿真结果进行后处理，得到图4所示的各因素水平下汇流集管中心轴线（4a黑色虚线）截面位置的气流速度云图和各汇流入口支管的入口流速，以及图5所示的集管中心轴线位置的压力及速度变化曲线。为进一步探究集管中心轴线位置处的气流流动状态对管路气压损失的影响，建立入口支管气流分配一致性评价指标，如式7所示。

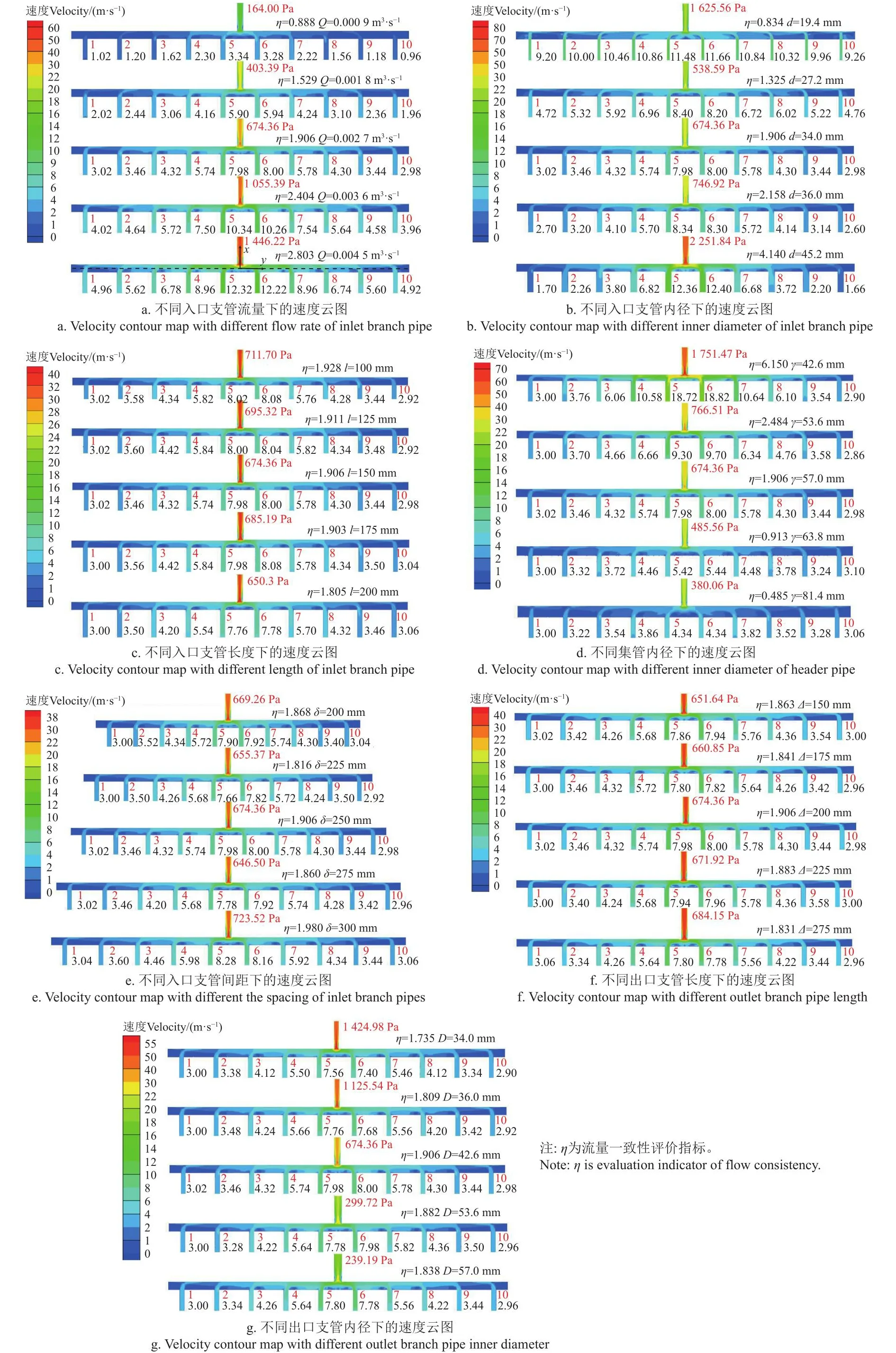
图4 各因素对多分支汇流管路气流场速度的影响Fig.4 Effect of factors on velocity of airflow field of multi-branch convergence pipe

式中η为入口支管流量一致性评价指标；j为入口支管编号；为入口支管1～10的平均入口流量，m3/s；为各入口支管气流入口流量，m3/s。

3.1.1 入口支管1流量对ΔP的影响

入口支管1的Q值变化对管路内部流场及ΔP的影响如图4a、图5a所示。由图可知，ΔP、η随Q的增加而增加，并在集管中心轴线位置出现明显的压力、速度梯度变化，且变化幅值随Q的增加而增大。方差分析表明F=4 275.87＞3.05=F0.01，Q值变化对ΔP影响显著。

分析图4a、图5a可知，当Q较小时，集管中心轴线处的压力、速度变幅较小，集管气压对η的影响较小，η的变化主要由气流在各入口支管中的沿程阻力损失决定；气流进入集管后，可以在较小的集管压差作用下克服惯性力完成转向，减少了与迎风侧壁面碰撞所造成的局部阻力损失，因此ΔP也较小。随着Q的增加，集管轴线处的压力、速度变幅增大，集管气压对η的影响增加；由于各入口支管内气流流速增大，进入集管的气流受自身惯性影响加大，需要更大的集管压差来使其完成转向，继而使ΔP持续增加。

3.1.2 入口支管内径对ΔP的影响

d值变化对管路内部流场及ΔP的影响如图4b 、图5b所示。由图可知，随着d的增加，ΔP先减小后增加，η逐渐增大，集管轴线压力递增明显，速度先递减后递增。方差分析可知F=7 083.91＞3.26=F0.01，d对ΔP影响显著。

分析图4b、图5b可知，当d较小时，集管气压对于η的影响较小，气流在入口支管内的沿程损失决定了η的大小；在Q相同时，d越小，入口支管内气流流速越高，气流在支管中的沿程损失越大，进入集管后的气流惯性作用大于集管压差作用，在与迎风侧壁面撞击后增大了气流的局部损失，故此时ΔP较大。随着d增加，集管压差成为影响η的主要因素，压差变幅越大，η越大；同时d的增加降低了入口支管流速，气流自身惯性作用减弱，集管压差对气流转向的影响加大，气流与集管迎风侧壁面碰撞所产生的局部阻力损失减少；但随着d继续增加，集管与外界压差也相对减小，使相同流量的气流流入支管需提供更大的集管压差，因此ΔP又明显增加。

3.1.3 入口支管长度对ΔP的影响

l对管路内部流场及ΔP的影响如图4c、图5c所示。由图可知，ΔP和η随l的增加而降低，集管轴线压力呈两侧对称的阶梯状分布，且各水平差异明显，速度呈两侧对称的跃阶式分布，但各水平差异不大。由方差分析可知F=1 808.76＞3.26=F0.01，l对ΔP影响显著。

结合图4c、图5c分析可知，l的增加增大了各入口支管气流的沿程阻力损失，因此l越大，进入集管的气流流速越低，气流受惯性作用碰击集管迎风侧壁面而产生的局部损失越小，因此ΔP逐渐减小。但此时集管压差是影响η的主要因素，因此，集管压差变动的剧烈程度反映了η的大小。

3.1.4 集管内径对ΔP的影响

γ对管路内部流场及ΔP的影响如图4d、图5d所示。由图可知，ΔP和η随γ的增加而降低；集管轴线的压力和速度分布逐渐趋于平缓。由方差分析可知F=7 900.01＞3.26=F0.01，γ对ΔP影响显著。

分析图4d、图5d可知，γ与d的比值随γ的增加而增大，此时支管气流流入集管的突扩环境后会瞬间减速，气流与集管迎风侧壁面碰撞所形成的局部损失降低，集管内压差下降，ΔP降低。同时随着γ的继续增加，集管轴线压差变化趋于平缓，气流在各入口支管中的沿程损失成为影响η的主要因素。

3.1.5 入口支管间距对ΔP的影响

δ对管路内部流场及ΔP的影响如图4e、图5e所示。由图可知，ΔP和η随δ的增加呈现连续的递减递增趋势；集管轴线压力、速度分别呈两侧对称的阶梯状、跃阶式分布。由方差分析可知F=11.85＞3.05=F0.01，δ对ΔP影响显著。

分析图4e、图5e可知，各水平的η值仍主要取决于集管压差变化，随着δ的增加，η值随集管压差的变化呈现连续的递减递增变化趋势。当δ<0.25 m时，入口支管气流与集管迎风侧壁面碰撞所产生的局部损失、沿集管流动的沿程损失、在集管中汇聚所产生的局部损失等共同影响着出口支管的ΔP，ΔP先降后增；当0.25 m≤δ≤0.275 m时，入口支管间距增加，气流在集管中汇聚所产生的局部损失减弱，导致ΔP下降；当δ＞0.275 m时，气流沿集管流动的沿程损失增大，导致ΔP增加。

3.1.6 出口支管长度对ΔP的影响

Δ变化对管路内部流场及ΔP的影响如图4f、图5f所示。由图可知，随着Δ增加，ΔP总体呈递增趋势，η呈连续的递减递增趋势；集管轴线压力、速度分别呈两侧对称的阶梯状、跃阶式分布。方差分析可知F=8.49＞3.53=F0.01，表明Δ对ΔP影响显著。

分析图4f、图5f可知，集管压差变化决定了各水平的η，集管压差梯度越大，η越大。同时随着Δ的增加，自集管汇流进入出口支管中的气流行程增加，沿程损失增大，故ΔP随之增加。

3.1.7 出口直管内径对ΔP的影响

D对管路内部流场及ΔP的影响如图4g、图5g所示。由图可知，随着D的增加，ΔP呈显著的递减趋势，η呈先升后降的趋势；集管轴线压力、速度分别呈两侧对称的阶梯状、跃阶式分布。方差分析可知F=6 700.08＞3.9=F0.01，D对ΔP影响显著。

分析图4g、图5g可知，各水平η随集管压差的变化而变化。D的增加使出口支管与集管的压差减小，自集管汇流至出口支管的气流减速，气流在集管与出口支管交界处汇流而产生的局部损失降低，在出口支管内流动的沿程损失亦降低，故ΔP显著下降。

综上可知，多分支管路出口支管边界与入口支管边界的压差是管内气流形成流动的主要原因，在压差的作用下，气流自外界流入入口支管1～10，并分别在入口支管与集管交界位置完成转向继而在集管内流动，最后汇流至出口支管流出。集管压差是影响总体压力损失和各入口支管气流分配一致性的主要原因和流体力学机理，集管压差梯度越大，ΔP越大，η越高。这也阐释了多分支汇流管路的几何结构差异对集管压差变化的直接影响，并同时影响到气流在不同的几何结构管路流动时的沿程阻力损失与局部阻力损失，最终影响ΔP与η。

3.2 全尺寸模型台架试验结果与Π方程的拟合

全尺寸模型台架试验于华南农业大学工程学院农业工程楼开展，试验材料、测量仪器与单因素试验相同，试验台架及试验用多分支汇流管路如图6、图7所示。

图7 台架试验用多分支汇流管路Fig.7 Multi-branch convergence pipe for bench test

根据表4的Π方程试验方案，选取不同因素水平下的多分支汇流管路开展试验，每组试验开展5次，试验结果取平均值，试验过程中，通过调节空调温度保持室内恒温（25 ℃），以保证ρ、μ值稳定。试验结果及各拟合方程如表6所示。

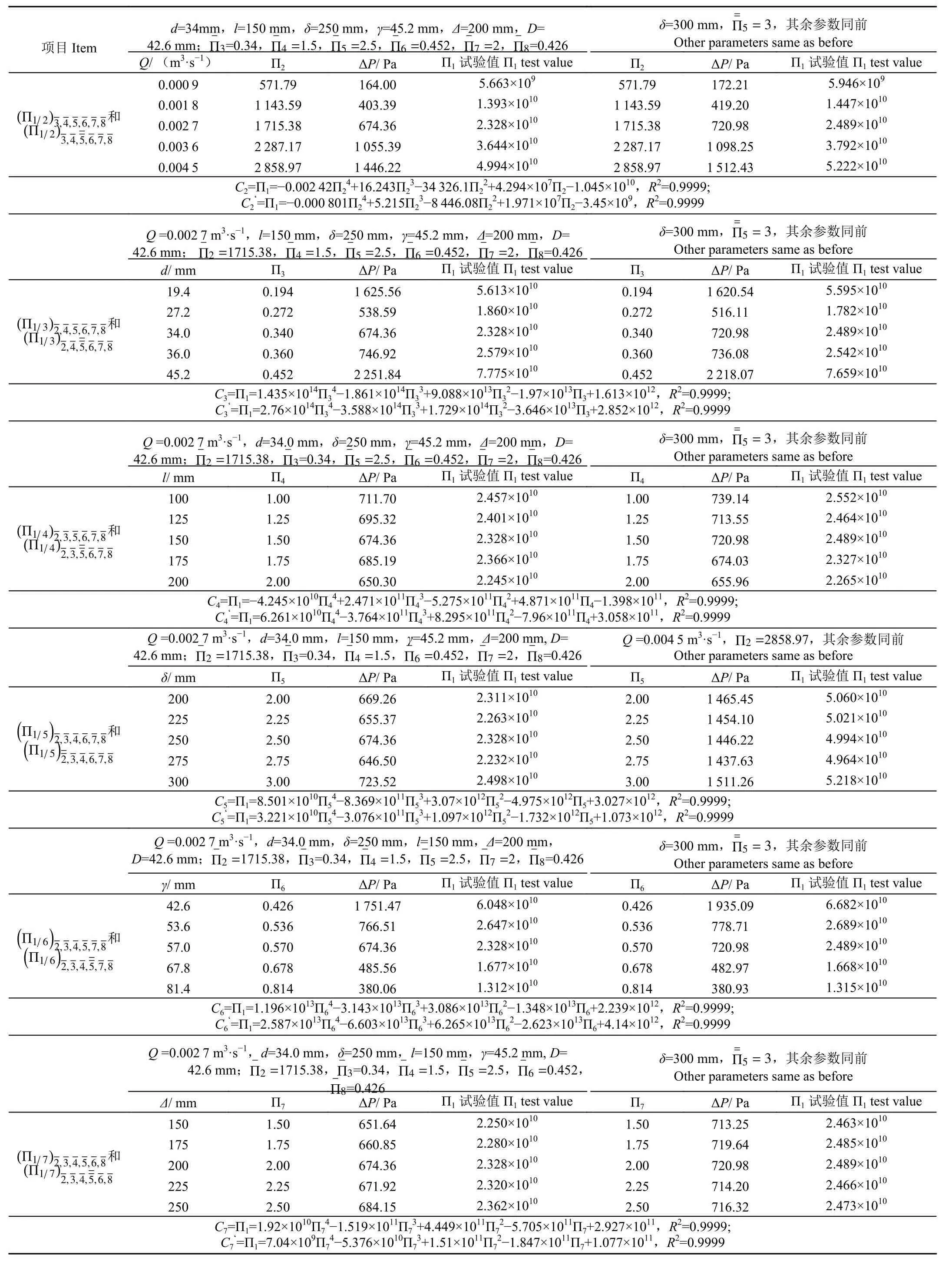
表6 试验结果和拟合方程Table 6 Results and fitting equation

3.2.1 Π方程的拟合

Π方程由各分量拟合方程的乘积组合而成，则出口支管Π1的方程为[25]

式中C2～C8由表6获取，上述函数表达式均为无量纲值。

3.2.2 Π方程的有效性验证

Π方程及ΔP计算结果共进行3次有效性验证，验证方法如下[22,25]：1）将Π方程计算的ΔP值和Π1值与每个测点的试验值进行比较；2）将Π方程的ΔP值和Π1值与各方程拟合曲线两侧以外工况的试验值进行比较；3）考虑经验公式应用范围内的其他试验条件。

1）第一次有效性验证

将每个测点的参数转换成相应的Π值，分别带入式（8），获得相应的Π1值和ΔP值，然后将方程计算结果与试验值进行比较，如表7所示。由表7可知，Π方程计算结果与试验值的偏差远小于10%，在可接受的范围内[33]，因此方程（8）是相对准确。

表7 Π方程的第一次有效性检验结果Table 7 The first validity experimental result of the Π equations

2）第二次有效性检验

表8 Π方程的第二次有效性检验结果Table 8 The second validity experimental result of the Π equations

二次验证结果表明，当571.79≤ρQ/μh≤2 858.97，0.194≤d/h<0.272、0.272

3）第三次有效性检验

为了进一步验证第二次有效性验证的结论，选取试验参数范围内的其他点（不同于Π方程构建时的测试点），进行验证试验，结果如表9所示。结合第二次验证结果可知，当1 442.19≤ρQ/μh≤2 020.34、0.21＜d/h≤0.28、1.4≤l/h≤1.6、2.4≤δ/h≤2.8、0.452≤γ/h≤0.638、2.1≤Δ/h≤2.4即0.002 27 m3/s≤Q≤0.003 18 m3/s、21.0 mm

表9 Π方程的第三次有效性检验结果Table 9 The third validity experimental result of the Π equations

综上所述，Π方程和经验公式可用于0.000 9 m3/s≤Q≤0.004 5 m3/s，28.0 mm≤d≤45.2 mm，100 mm≤l≤200 mm、200 mm≤δ≤300 mm，42.6 mm≤γ≤81.4 mm，150 mm≤Δ≤250 mm，34.0 mm≤D≤42.6 mm、53.6 mm≤D≤57.0 mm的范围条件，此时经验公式计算所得的ΔP值对多分支汇流管路总体压力损失的预测误差小于10%。

结合Π方程的有效性检验结果，联立式（6）、式（8），进一步简化后可得多分支汇流管路总体压降损失ΔP为

式中λ∈(Q,d,l,δ,γ,Δ,D)，当λ为Q时，ξ为其他量对应函数的乘积，其值为管路初始尺寸值，此时ξ可结合实际试验取值为0.99～1.03。当λ为除Q外的任一个量时，ξ为集合内剩余量对应函数的乘积，其值为管路初始尺寸值，此时ξ可结合实际试验取值为2.305×1010～2.398×1010。

4 结 论

本文对气吸式播种机气力系统多分支汇流管路出口支管的总体气压损失进行了探究，明确了影响管路气流能量损耗的主要因素。采用单因素试验、Fluent仿真模拟及量纲分析法，从微观和宏观角度分析了多分支汇流管路中气压损失和气流分配机理，构建气压损失定量预测模型，并得到如下结论：

1）通过单因素试验并结合Fluent仿真模拟，确定了影响多分支汇流管路内流体流动及管路总体压力损失的主要试验因素为入口支管流量（Q，m3/s）、入口支管内径（d，mm）、入口支管长度（l，mm）、入口支管间距（δ，mm）、集管内径（γ，mm）、出口支管内径（D，mm）和出口支管长度（Δ，mm）。分析了各因素对管路总体压力损失ΔP的具体影响机理，明确了集管压力变化是影响各入口支管气流分配一致性的主要原因，也是导致多分支汇流管路各入口支管气流分配不均的流体力学机理。

2）通过全尺寸模型试验，采用量纲分析法建立了多分支汇流管路总体压力损失的预测经验公式，在0.000 9 m3/s≤Q≤0.004 5 m3/s、28.0 mm≤d≤45.2 mm、100 mm≤l≤200 mm、200 mm≤δ≤300 mm、42.6 mm≤γ≤81.4 mm、150 mm≤Δ≤250 mm、34.0 mm≤D≤42.6 mm、53.6 mm≤D≤57.0 mm的条件下，所建立的经验公式对压力损失ΔP的预测误差小于10%，满足一般工程领域的要求。研究结果可为气吸式播种机气力系统的管路设计与优化提供参考。