基于机器学习的岩芯渗透率及裂缝开度预测

陈 林 ，黎棚武，张绍俊，李志杰，杜小勇

1.中国石油塔里木油田分公司油气工程研究院，新疆 库尔勒841000

2.油气藏地质及开发工程全国重点实验室·西南石油大学，四川 成都610500

引言

塔里木盆地致密砂岩气藏储量丰富，经过多年的勘探开发，已成为中国致密气开采稳步提升的战略要地。致密砂岩储层低孔低渗，开采难度大。与常规气藏相比，致密砂岩气藏孔喉细小，毛管压力高，黏土矿物含量高，在开发过程中极易受到敏感性损害，影响开发效果及产能[1-4]。裂缝和微裂缝是其主要的渗流通道[5-6]，因此，常有“保护裂缝为主，同时兼顾基质”的储层保护对策，但裂缝通常具备较强的应力敏感[7]，保护难度大。研究应力敏感损害下致密砂岩气藏裂缝和基质岩芯渗透率的变化规律并根据规律预测岩芯渗透率，一直是国内外学者关注的焦点。

20 世纪末，众多学者开展了渗透率预测方面的研究。1996 年，Huang 等[8]基于不同的测井曲线，运用反向人工神经网络预测渗透率，得到实测渗透率与人工神经网络预测渗透率的相关系数为0.8；2013 年，Liu 等[9]基于理论煤基质收缩应变，将理论应变模型结合到渗透率预测模型中，结果表明预测值与现场观测值契合度很高；2018 年，张路锋等[10]模拟裂缝岩芯，发现可通过缝宽预测渗透率，岩芯渗透率与缝宽呈三次方关系；蔡李梅等[11]建立了基于孔隙度、粒度及裂缝发育指数的地震-地质约束的多参数渗透率综合预测模型，实现高精度的致密砂岩储层渗透率单井、平面预测。2020 年，程辉等[12]分别评价并优选了更适用于致密砂岩岩芯的基于高压压汞和核磁共振的渗透率预测模型；张鹏等[13]分析筛选了等效缝宽、孔洞平均直径、非碳酸盐矿物含量等11 个应力敏感伤害主控因素，通过BP 神经网络法预测碳酸盐岩储层应力敏感程度，然而，该模型并未考虑方解石含量和白云石含量等与应力敏感性伤害率显著相关的影响因素；陈龙伟等[14]以沁水盆地煤系地层为例，提出利用地震资料曲率属性预测地应力，根据渗透率与地应力的幂指数关系式，将地应力转换为渗透率，该方法预测结果与实钻井吻合程度较高。2021 年，谷宇峰等[15]以姬塬油田西部长4+5 段致密砂岩储层测井资料为基础，基于机器学习的数据分析性能，利用梯度提升决策树（Gradient Boosting Decision Tree,GBDT）技术预测致密砂岩储层渗透率，该方法只需要测井数据，且模型精度较高；谷宇峰等[16]还提出利用PSO 算法改进极限梯度提升算法（eXtreme Gradient Boosting,XGBoost），进而提出PSO-XGBoost 渗透率预测模型优化参数；闫国峰等[17]基于压降试井测试原理，以压裂施工曲线为基础，考虑压裂液漏失和裂缝扩展综合影响，建立了致密油储层压裂后渗透率预测数学模型，利用压裂施工数据计算压裂后的渗透率；景文龙等[18]以随机生成的数字岩芯的孔隙度和渗透率作为机器学习的数据库，数据进行提取和处理，建立了任意岩芯的孔隙度渗透率预测模型。综上可见，当前学者建立的渗透率预测模型对测井资料的依赖性较强，考虑的渗透率影响因素还不够全面，在裂缝性致密砂岩中运用还具有一定的局限性。

为此，本文基于岩石自身属性数据如初始孔渗、孔喉半径和黏土矿物含量等，采用机器学习多元线性回归算法，分析挖掘各物性参数与应力敏感损害下的岩芯渗透率之间的关系，耦合围压渗透率关系模型和K−p函数参数预测模型，从而建立应力敏感损害下的岩芯渗透率预测模型和裂缝开度预测模型，并通过决定系数、均方根误差和相对误差检查模型精度。该模型对输入数据依赖性弱、适用范围广，根据岩石基础物性和矿物成分含量即可预测不同围压下岩芯渗透率，对裂缝性致密砂岩气藏的储层伤害评价、储层保护对策和生产模拟预测具有指导作用。

1 多元线性回归模型

1.1 模型建立

线性回归是机器学习数据挖掘中的基础算法，能够对一个或者多个自变量和一个因变量线性关系进行分析。在处理大量数据和较少的数据特征时，多元线性回归是寻找输出参数和输入参数之间线性关系的最常用的模型[19]。对于n个自变量，多元线性回归模型如式（1）所示，当n=1 时为一元线性回归。

1.2 模型验证

1.2.1 决定系数

决定系数可以根据拟合程度来评估方程的预测能力。决定系数取值为[0，1]，决定系数越接近于1，则预测精度越高；决定系数越接近于0，预测精度越低。决定系数为相关系数的平方，相关系数计算公式为

1.2.2 均方根误差与相对误差

均方根误差是均方误差的算术平方根，均方根误差是各数据偏离实测值差值的平方和的平均数，均方根误差越小，说明模型预测准确度越高[20]。

N个数据均方根误差公式为

相对误差可以反映实测值和预测值偏离程度，可以用来比较模型预测精度。相对误差为实测值与预测值之差的绝对值与实测值的比值

2 实例运用

2.1 数据获取

本文以塔里木盆地克拉苏构造带岩样为例建模分析。如图1 所示，克拉苏构造带致密砂岩储层基础物性差、低孔隙度、低渗透率，黏土矿物含量高，含水饱和度高，应力敏感性及非均质性较强。发育的裂缝和微裂缝提高了储层的渗流能力[21-23]。

图1 部分岩芯铸体薄片Fig.1 The thin section of core

2.1.1 渗透率影响因素分析

要精确预测岩石渗透率，必须明确各种影响因素的权重占比并选择合适的主控影响因素。2001年，黄思静等[24]认为碳酸盐岩的组成、温度、压力以及石英胶结物对孔隙度和渗透率有重要影响；2003 年，Heiland[25]研究了不同应力下低孔隙度砂岩岩芯的渗透率变化，认为不同应力、岩石变形、岩石破坏和水力特性与渗透率有密切关系；2013 年，Arson 等[26]提出了一种模型，将渗透率与孔隙度联系起来，并且考虑了未损伤样品和裂纹样品（不同的损伤状态），该模型较好地反映了围压对损伤演化和渗透率变化的影响；2015 年，Ngo 等[27]收集越南Cuu-Long 盆地和松洪盆地砂岩和碳酸盐岩，分析其孔隙度、常规岩芯分析渗透率数据和注汞毛细管压力的孔喉尺寸，利用水力流动单元（HFU）进行渗透率预测；2019 年，Li 等[28]发现孔隙的分布非均质性和各向异性与渗透率有关，并探讨了微观影响机理；2021 年，熊繁升等[29]认为含多孔介质宏观渗透率与孔隙度、纵横比、裂缝（软孔隙体）密度等参数有关。根据塔里木盆地克拉苏构造带实际情况可知，影响渗透率的因素主要是储层岩性与物性，其中，不同的矿物组成及含量直接影响致密砂岩的渗透率变化。目前，针对岩石渗透率和岩性及物性的关系，学者们普遍认为：

1）黏土含量越高，储层的孔隙度和渗透率越低。黏土矿物遇水膨胀，形态结构也会发生变化，从而封堵喉道，降低储层渗透率。

2）长石为易溶的不稳定矿物，是次生孔隙形成的物质基础，在溶蚀作用下形成高岭石，堵塞孔隙和喉道，长石含量越高，储层的孔隙度和渗透率都降低。

3）致密砂岩的孔隙度与渗透率具有一定的正相关性，低渗低孔的致密砂岩岩样具有更强的应力敏感性。

在应力敏感实验中，发现不同围压下岩芯渗透率的变化规律与岩石的矿物成分与内部结构存在一定关联。通过多因素权重分析，选取了属于岩石物性（初始孔隙度、初始渗透率、中值孔喉半径和最大孔喉半径）和矿物组分含量（钾长石、方解石、蒙脱石、斜长石、伊利石、高岭石、绿泥石和胶结物）的12 个岩石渗透率影响因素。

2.1.2 岩芯数据获取

岩芯裂缝对岩芯渗透率影响明显，非裂缝性岩芯与裂缝性岩芯的应力敏感程度有所差异[30-31]，因此，本文区分了裂缝性岩芯和非裂缝性岩芯，在明确影响岩石渗透率的包括物性和矿物成分在内的12个影响因素后，通过实验及文献调研，收集了该区块裂缝性岩芯和非裂缝性岩芯基础物性参数（表1）及岩芯样品矿物组分含量共150 组数据（表2）。

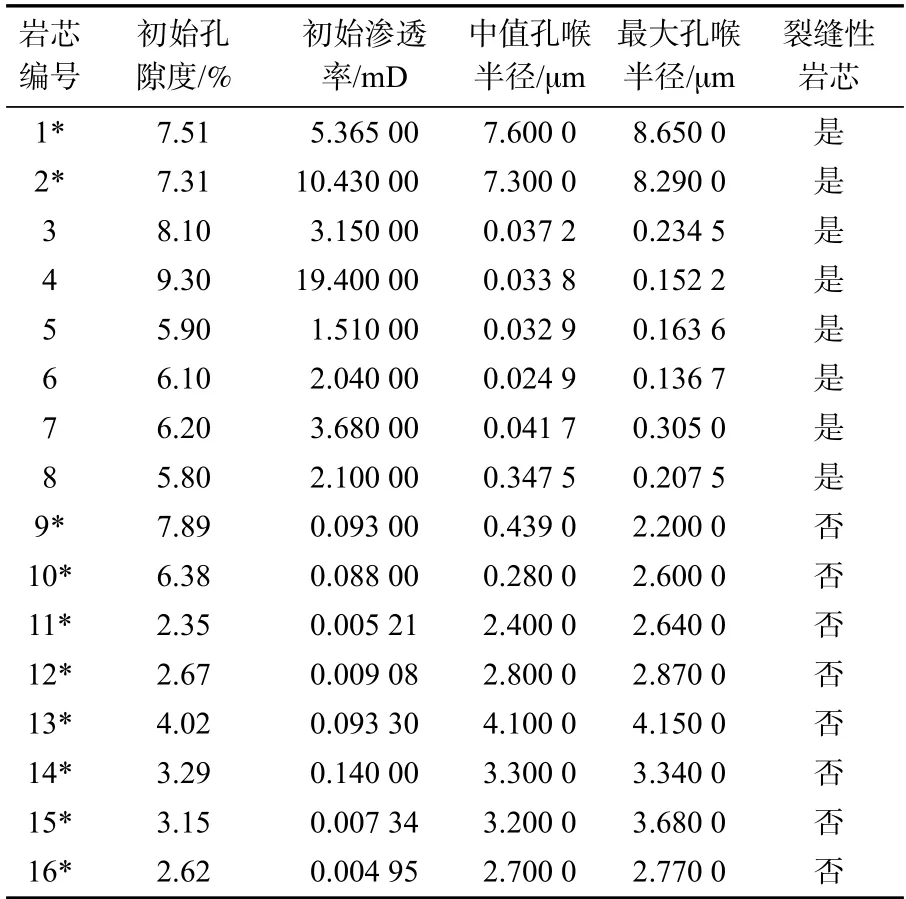
表1 部分岩芯样品基础物性参数Tab.1 Basic physical parameters of core samples

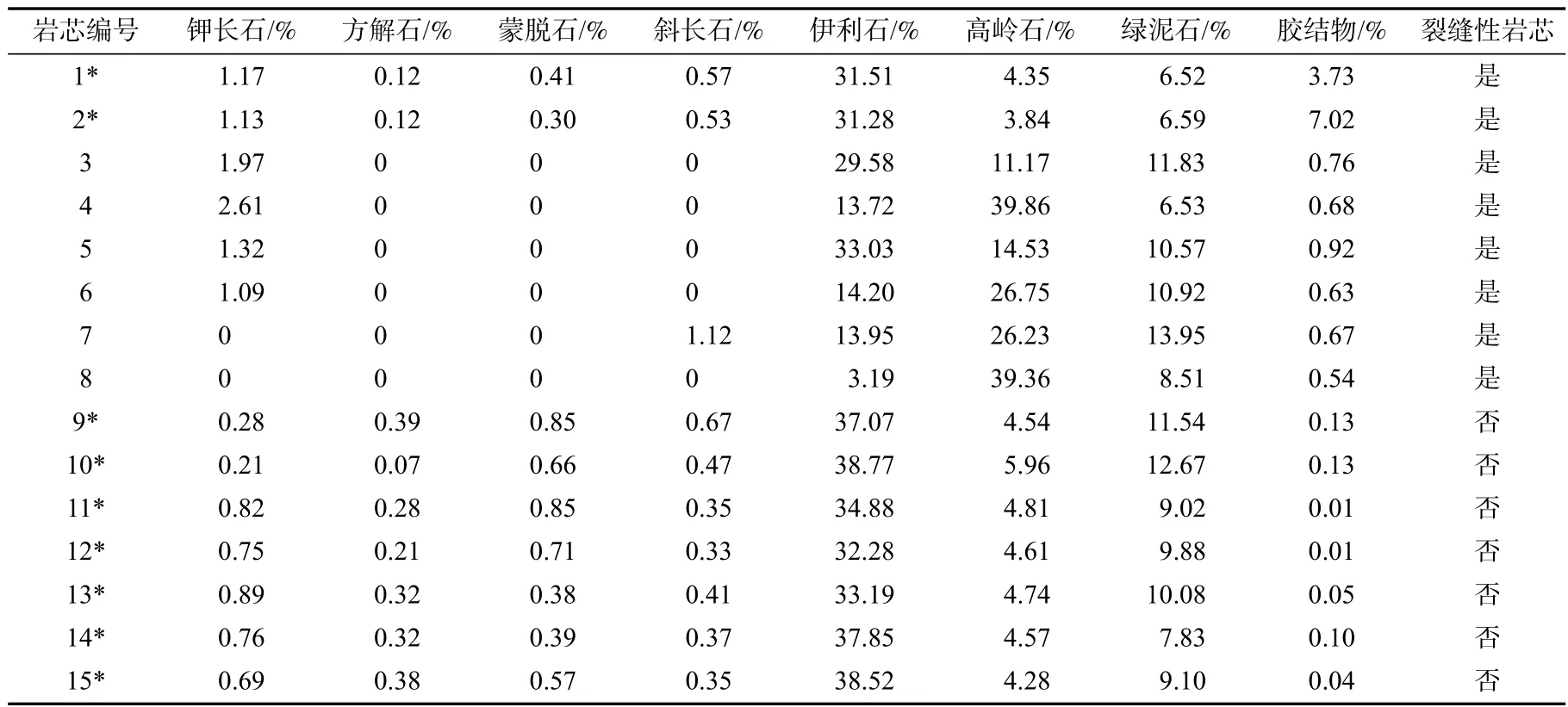
表2 部分岩芯样品矿物组分含量Tab.2 Mineral component content of core samples

2.2 数据预处理

数据预处理是建模前的重要步骤。由于实验及调研数据类型多样，数据精度与量纲存在一定差异，影响机器学习的收敛。因此，在建立预测模型前，需要对异常数据进行筛选[32]。本文筛选清除了大于3 倍平均值的实验数据，并剔除了部分不合理数据，从而降低实验数据误差，提高模型预测精度。

2.3 岩芯渗透率预测模型建立

2.3.1 模型建立流程

岩芯渗透率预测模型主要由两部分组成，见图2：基于应力敏感实验数据建立渗透率与围压关系模型；基于岩石成分和物性数据建立K−p函数参数预测模型。

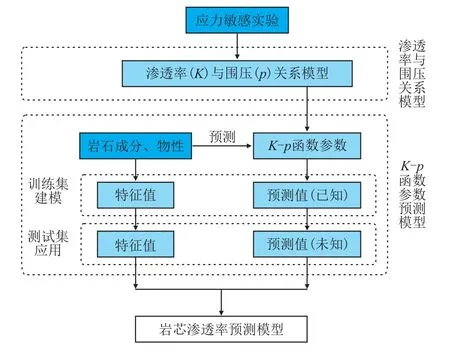
图2 岩芯渗透率预测模型建立流程Fig.2 The establishment process of core permeabilityprediction model

2.3.2 渗透率与围压关系模型

本文设计的岩芯渗透率预测和裂缝开度预测方法是建立在应力敏感实验的基础上，这里首先研究渗透率与围压之间的关系。随机选取3 组实验数据进行指数、线性、对数及幂函数关系式的拟合，通过决定系数来判断拟合效果，拟合关系见表3。

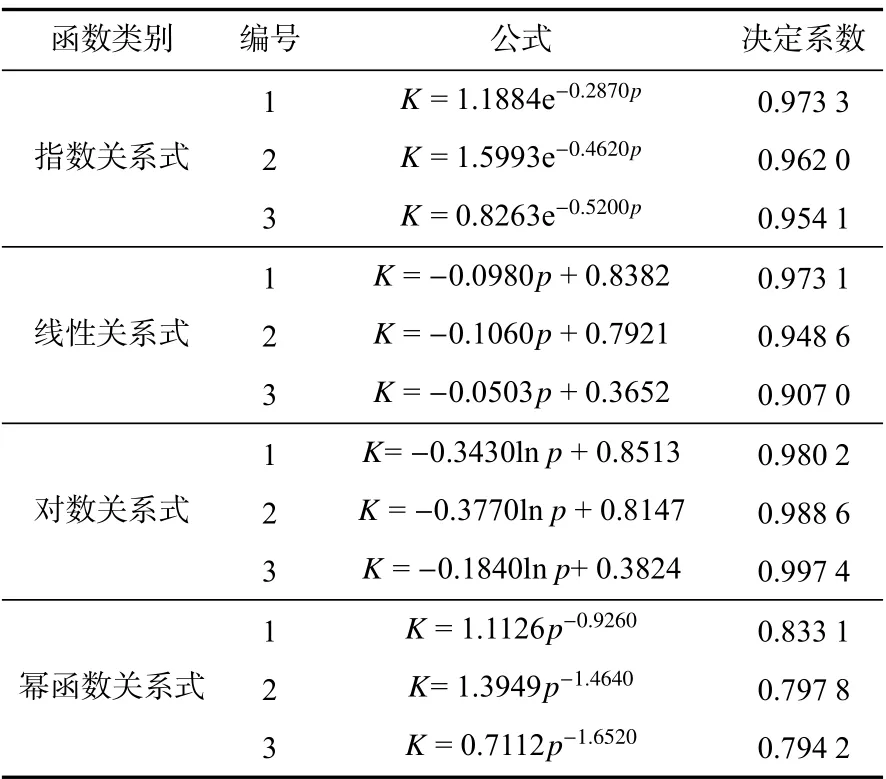
表3 围压与渗透率关系式Tab.3 Relationship between confining pressure and permeability

由表3 可知，对数关系式的决定系数最高，最高为0.997 4；幂函数的决定系数普遍较低，最低为0.794 2；说明渗透率和围压关系最符合对数关系函数，K−p函数数值上的关系式为

式中：

2.3.3K−p函数参数预测模型

基于属于岩石物性和岩石成分两大类的12 个渗透率影响因素，建立多元线性回归模型，根据式（1），对应的回归式为

以收集数据的70%为训练集，30%为测试集。通过基于梯度下降的线性回归模型对训练集数据进行拟合，拟合结束后使用均方根误差评价模型预测精度，并绘图进行比较。随后输入测试集数据得到测试值，得到结果。模型的处理数据流程如图3所示。

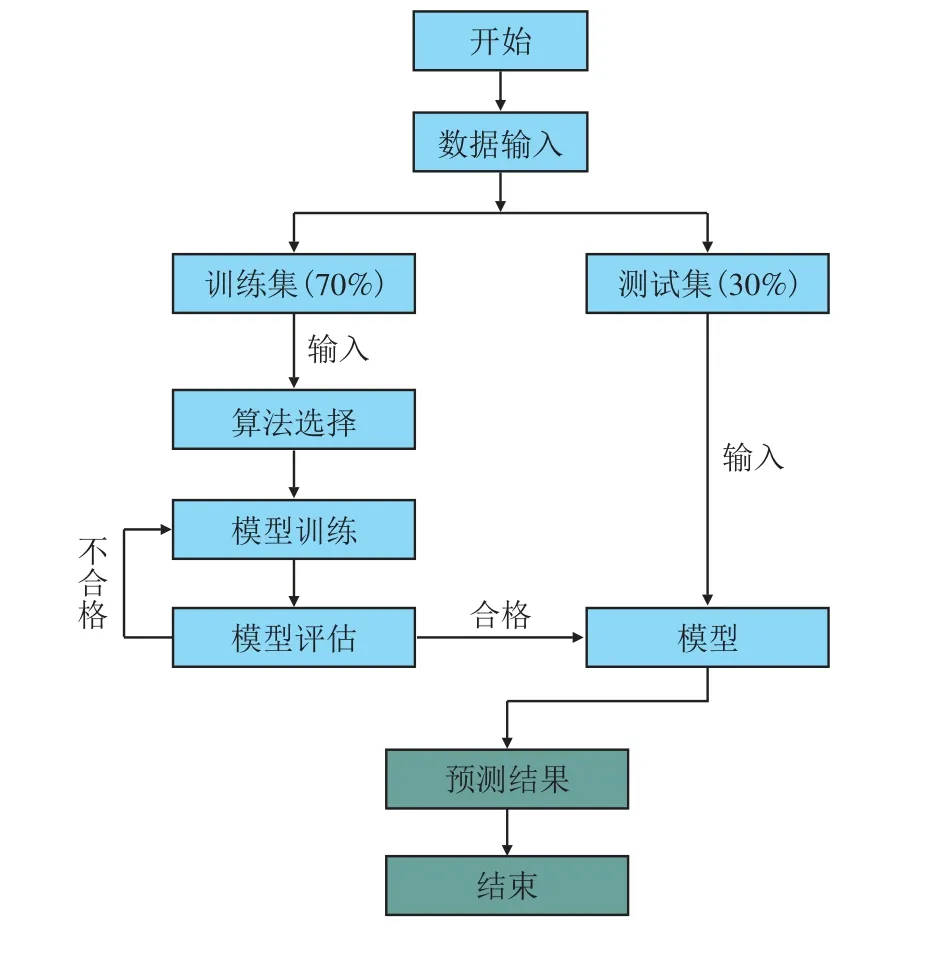
图3 数据处理流程示意图Fig.3 Flow chart of data processing

2.4 岩芯渗透率预测模型精度

2.4.1 渗透率和围压关系模型精度

随机选取部分裂缝性岩芯和非裂缝性岩芯实测数据进行验证，验证结果如表4 所示。

由表4 可见，在裂缝性岩芯中，预测结果决定系数均较高，为0.925 5∼0.991 5，决定系数平均值为0.962 5；非裂缝性岩芯预测结果决定系数为0.906 9∼0.997 4，平均值为0.965 6，略高于裂缝性岩芯，但非裂缝性岩芯中决定系数范围更大，预测结果的精度较裂缝性岩芯更不稳定。

2.4.2K−p函数参数预测模型精度

K−p函数参数预测模型预测值均方根误差和相对误差如表5 所示，可以看出，对非裂缝性岩芯渗透率，ERMS(a)=3.435、ERMS(b)=3.517；而对于裂缝性岩芯，ERMS(a)=0.043、ERMS(b)=0.208，这说明非裂缝性岩芯中均方根误差较低。然而，由于两种岩芯中a、b的量级大小存在差距，裂缝性岩芯的相对误差反而更低，说明裂缝性岩芯的预测精度更高。从图4∼图7 也可发现，裂缝性岩芯中a和b的预测值和实测值拟合效果更好。

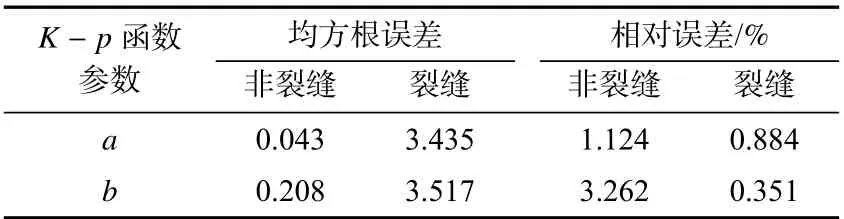
表5 预测值与实测值的均方根误差和相对误差Tab.5 The root mean square error and relative error of predicted_____________________value and actual value

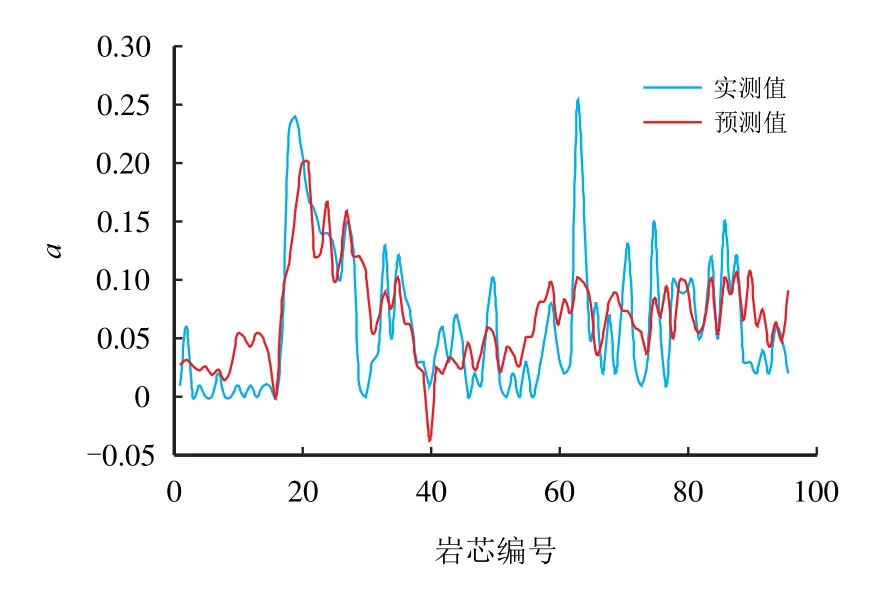
图4 非裂缝性岩芯中a 的预测值与实测值Fig.4 Deviation between predicted and experimental values of a in non-fractured cores

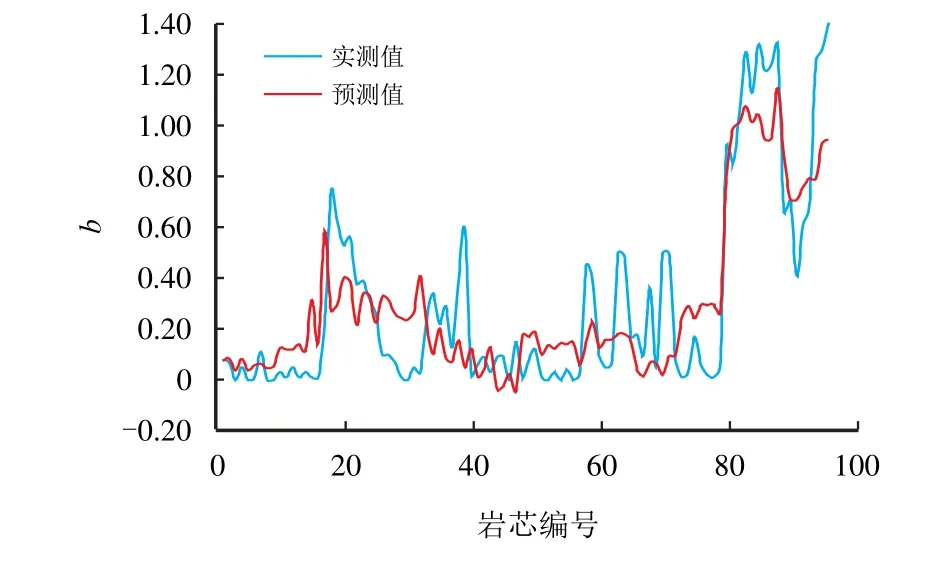
图5 非裂缝性岩芯中b 的预测值与实测值Fig.5 Deviation between predicted and experimental values of b in non-fractured cores

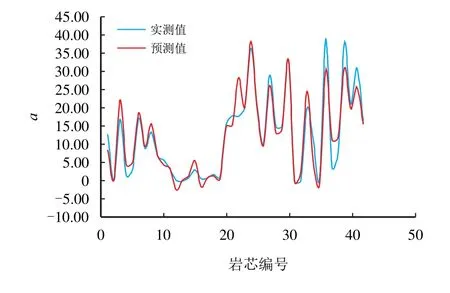
图6 裂缝性岩芯中a 的预测值与实测值Fig.6 Deviation between predicted and experimental values of a in fractured cores

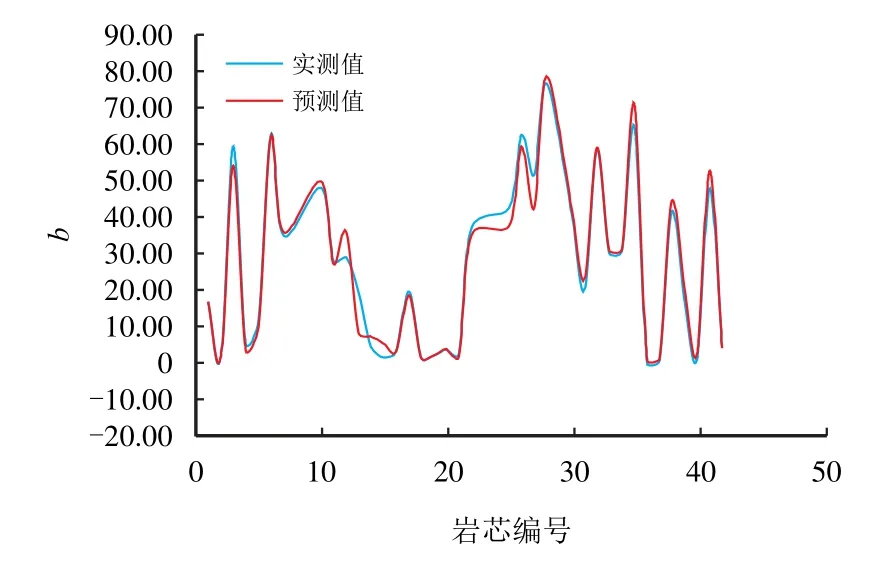
图7 裂缝性岩芯中b 的预测值与实测值Fig.7 Deviation between predicted and experimental values of b in fractured cores

2.5 裂缝开度预测模型

裂缝开度是开展裂缝动态变化的基础储层参数，也是在钻井堵漏中优化堵漏颗粒粒径大小的重要参数。因此，准确评价裂缝开度对油气田开发具有极其重要的实际意义[33-34]。微裂缝开度可以导致岩芯渗透率的变化，由于微裂缝开度难以测量，本文拟建立裂缝开度和渗透率之间的关系，旨在通过渗透率数据反推裂缝开度，从而减轻实验工作量。通过对塔里木地区的渗透率和裂缝开度数据进行拟合，研究发现，该地区的裂缝开度和渗透率基本符合函数关系式（7），其中，岩芯渗透率可以是岩芯实际渗透率，也可以是岩芯渗透率预测模型预测所得的渗透率。

式中：W--裂缝开度，mm。

预测值与实测值的对比曲线如图8 所示，该拟合式线性回归决定系数为0.978 3，预测精度高。在地层发生漏失时，可基于预测的裂缝开度优化堵漏材料的颗粒粒径，提高封堵成功率，实现地层高效堵漏。

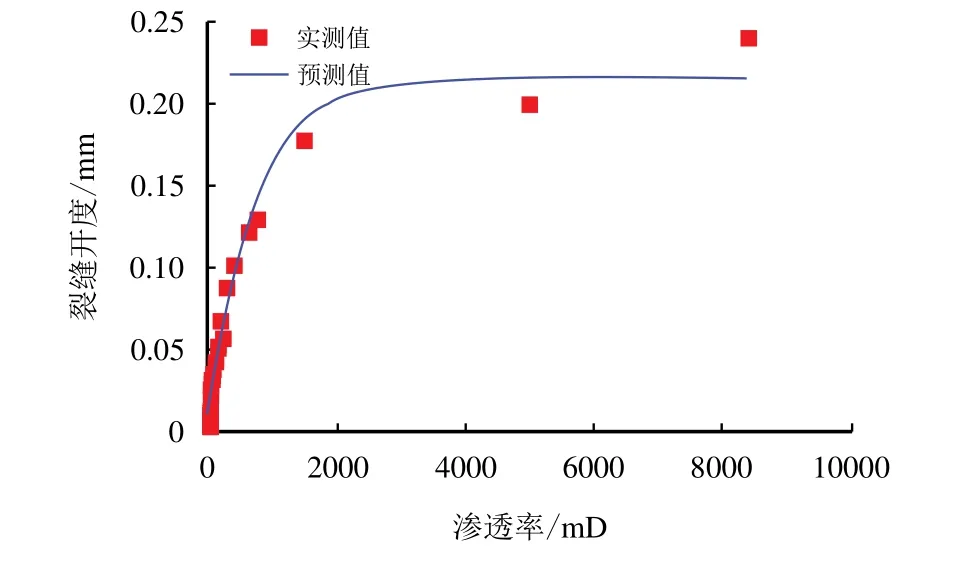
图8 渗透率与裂缝开度关系预测曲线与实际曲线对比Fig.8 The comparison of forecast curve of permeability and fracture width with the actual curve

3 结论

1）围压渗透率关系模型在裂缝性岩芯中预测结果决定系数平均值为0.962 5，在非裂缝性岩芯中预测结果决定系数平均值为0.965 6，裂缝性岩芯中围压渗透率关系模型预测结果的精度更稳定。

2）K−p函数参数预测模型预测结果在裂缝性岩芯中的均方根误差高于非裂缝性岩芯，但裂缝性岩芯的相对误差要低于非裂缝性岩芯。综合来看，岩芯渗透率预测模型更适用于裂缝性岩芯。

3）裂缝开度预测拟合式的决定系数为0.978 3，预测精度较高。