Euler-Bernoulli 海洋立管涡致强迫振动响应研究
2023-08-02李映辉邵永波
赵 翔 ,谭 明,李映辉,邵永波
1.西南石油大学土木工程与测绘学院,四川 成都610500
2.西南交通大学力学与工程学院,四川 成都610031
引言
随着陆地油气资源的不断开采,其储备量逐渐枯竭,包括中国在内的许多国家都将目标转向了海洋。在海洋油气开采的过程中,海洋立管是极其关键的设备之一,主要连接海上悬浮平台与井口,为采集油气提供输送管道。海洋立管在工作时受复杂的工作环境以及洋流、波流等各种动态荷载的影响,会引起立管的振动[1],因此,研究海洋立管的振动特性,确保海洋立管的安全性以及稳定性尤为重要。
PIP 系统作为一种海洋管道结构,具有较好的抗振效果,近年来得到了广泛应用。PIP 系统通常由外部管道、内部管道和填充在两个管道之间的绝缘层3 部分构成。通过绝缘层连接外部和内部管道的系统以及由大量舱壁连接的系统是常见的PIP 系统类型[2]。内部管道用于输送石油等流体,外部管道涂有防腐材料,并保护内部管道免受冲击。已经有许多研究人员通过分析或者实验的方式研究了PIP 系统的静态特性和动力学问题[3-4]。
PIP 系统在流体作用下发生涡致强迫振动是非常普遍的现象。当涡致强迫振动的频率接近PIP 系统自身的频率时,会产生大幅度的振动,从而形成较大威胁[5]。现有研究海洋立管受涡致强迫振动的响应方法有数值方法[6-9]和实验方法[10-12]。此前的研究工作中有关轴向拉力和阻尼对振动特性影响的研究较少[13]。实验方法获得的数据可靠但研究成本较高,而数值方法常用的是经验模型法中的尾流振子模型法,这种模型受到广泛认可。关于抑制立管振动的研究比较多,例如,增加不同截面形状的肋条,来研究其对振动响应的影响等[14]。尾流振子模型属于非线性振动模型,研究发现基于加速度模型来描述立管尾部流场的尾流振子模型更加适用[15]。本文采用的Lamb-Oseen 涡模型属于线性振动模型,这种线性模型在许多压电能量采集器的设计和实验中应用较多,它主要是吸收涡脱落的振动能量,并且在实验中有较好的效果。
海洋立管是一种细长结构体,其跨径比较大,并且管道的弯曲变形与剪切变形可以忽略不计,因此,本文采用Euler-Bernoulli 双梁模型对管道进行模拟[16-17]。基于Euler-Bernoulli 双梁模型,Zhang等[18]研究了在轴向压缩荷载作用下双梁系统自由振动问题。Mao 等[19-20]采用Adomian 分解方法研究了Winkler 层连接的双梁系统的自由振动问题。Abu-hilal 等[21]通过拉普拉斯变换得到了一般边界条件下Euler-Bernoulli 双梁模型稳态响应的格林函数。Li 等[22]建立了具有转动阻尼和平移阻尼的Timoshenko 梁模型,并得到了Timoshenko 梁稳态响应的格林函数。Zhao 等[23]研究了多裂纹Euler-Bernoulli 梁的受迫振动,得到了多裂纹梁的格林函数。他们所采用的梁模型以及格林函数法为本文的研究奠定了理论基础。
目前,对PIP 系统响应的研究主要是计算流体力学分析(Computational Fluid Dynamics,CFD)及实验方法,并未给出确定的解析解,对于PIP 系统响应的快速预测具有一定的阻碍。基于此,采用Lamb-Oseen 涡模型对PIP 系统的外激力建模来研究其涡致强迫振动问题,求解其涡致强迫振动问题的闭形式解析解,并对PIP 系统的响应进行快速预测,这对研究PIP 系统涡致强迫振动问题是十分有意义的。
本文对海洋立管的研究以横向振动为主,分析了Euler-Bernoulli 双梁模型在涡致强迫振动作用下的动力学响应。通过建模和拉普拉斯变换推导动力学问题的格林函数,得到了海洋立管的响应。通过数值分析,验证了双梁模型的正确性,并分别对不同管道直径、轴向拉力及外激力频率分析了系统响应的规律。
1 PIP 系统的模型和动力学响应
图1 给出了PIP 的模型示意图。管道系统的长度为L。外部管道的外径和内径分别为D1和D2,内部管道的外径和内径分别为d1和d2,U0表示流体的平均速度。PIP 系统通常具有很高的细长比[24-26],因此,采用Euler-Bernoulli 双梁模型,并且将中间绝缘层视为线性弹簧和阻尼器。
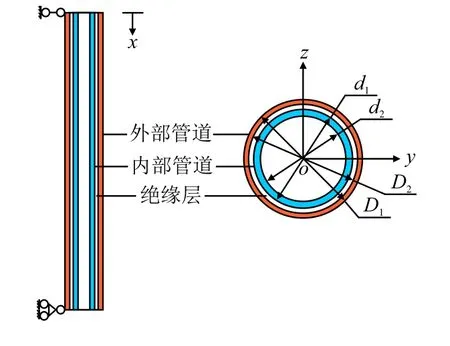
图1 PIP 系统示意图Fig.1 Schematic diagram of PIP system
1.1 格林函数的解
本文考虑了在涡致强迫振动影响下海洋立管的动力学响应,如图2 所示,建立系统的振动方程为[16-17]

图2 具有黏弹性层的双梁系统Fig.2 Double-beam system with a viscoelastic layer
格林函数是已经被证实的获得线性系统动态响应的有效方法[16]。双梁系统稳态强迫振动的格林函数是在单位谐波载荷作用下系统的动态响应。式(3)的格林函数解为
式中:δ()--狄拉克函数。
将式(4)中的x进行Laplace 变换和逆变换计算,可以推导出格林函数
式中:
当双梁体系受荷载时,控制方程的解为
2 外激力计算
图3 为流体对海洋立管作用的示意图。本文采用的是Lamb-Oseen 涡流模型。假设涡致强迫振动产生的外激力为简谐力:p(x,t)=P(x)eiωt,假设振动是周期性的,且管道上的力分布均匀,则P(x,t)只与时间相关,不随x的变化而变化。其中,f的表达式为[27]
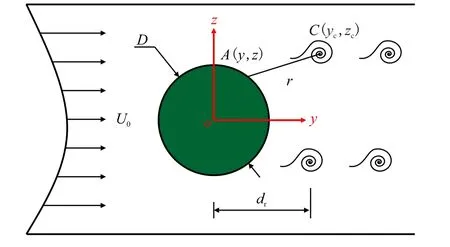
图3 涡致强迫振动对管道的作用示意图Fig.3 The action diagram of vortex-induced vibration on pipeline
在理论分析中,为了考虑涡流对立管的影响,漩涡产生的距立管中心最小和最大距离分别为0.5D和15.0D,超出此范围后漩涡不再对立管产生影响。此外,在理论分析中,外激力频率与涡流脱落频率相等,即可导出外激力幅值P(x)的表达式。
聚焦在一个稳定的涡面上,假设漩涡中心位置C(yc,zc),A(y,z)为外部管道上一点,速度为va。则A点和C点之间的压差为[27]
根据Lamb-Oseen 涡流模型假设和特性,单个涡流的运动可以分解为平均水平速度vc和旋转速度ωc,点A相对于涡流中心C的切向速度可以建模为
这种压差产生了主要作用在管道上的外激力,表达式如下
式中:l--海洋管道截面曲线。
将压差∆p代入式(14),得到
式(15)表明施加在管道上的外激力主要受涡流强度、位置和水平速度的影响。
其中
此外,平均流体速度U0可以近似为漩涡的平均水平速度vc。
文献[27]表明,当圆柱上的漩涡稳定时,zc=1.3D/2。从而得到外激力关于yc的关系,最后得到外激力达到最大时的位置yc。单位长度外激力幅值P(x)可表示为
再将P(x) 代入式(9),即可得到PIP 系统的响应。
3 数值分析与讨论
为了方便计算,管道长度取10 m,外部管道的外径D1=0.26 m,内径D2=0.22 m;内部管道的外径d1=0.20 m,内径d2=0.16 m;管道密度取7 850 kg/m3,弹性模量2.0×1011Pa,海水密度为1 025 kg/m3。
为了方便讨论,引入无因次量
3.1 解的有效性
3.1.1 格林函数解的有效性
实际上,当绝缘层的弹性模量以及阻尼为零时,忽略绝缘层质量,上述解就是单梁的格林函数。即g1(X;X0) 是k=0 情况下单梁的格林函数,并且在这种特定情况下,显然可知g2(X;X0)=0。图4显示了无因次挠度gi(X;0.5) 和无因次坐标X的函数。由图4可以看出,双梁系统的无因次挠度g1(X;X0)与单梁的无因次挠度g(X;X0)完全吻合,双梁系统的无因次挠度g2(X;X0) 为零,验证了本文方法的正确性。
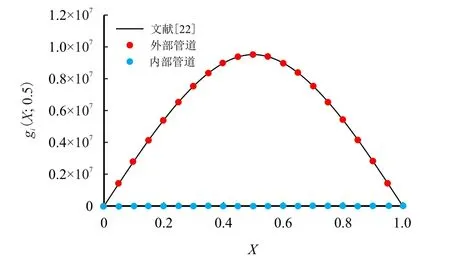
图4 解的有效性验证Fig.4 Validation of the solution
3.1.2 响应解的有效性
通过前面的计算,得到了PIP 系统涡致强迫振动位移响应,并且借助现有的研究结果与本文的结果进行对比验证,其基本参数如表1 所示。由于文献[28]中的立管为单管,所以在这里需要进行一些调整,令绝缘层的弹性模量以及阻尼为零,忽略绝缘层质量,从而退化成单立管模型,以方便数据的分析以及对比。
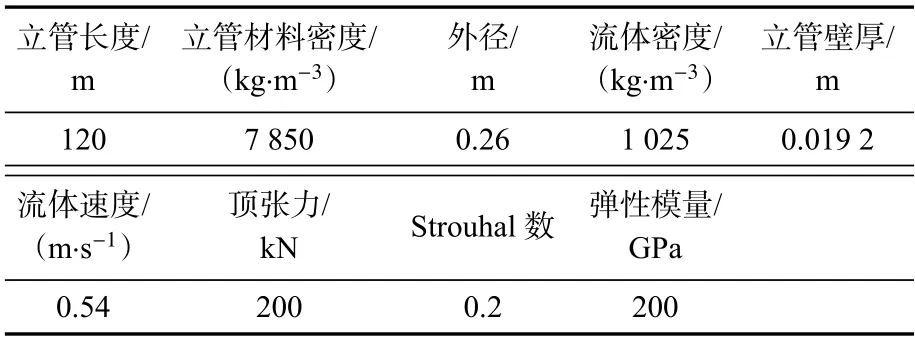
表1 基本参数Tab.1 Foundamental parameters
文献[28]中的数据是由柳军采用CFD 方法得到的海洋立管位移包络图。由于Lamb-Oseen 涡模型是将流体对PIP 系统的作用简化成均匀分布在管道上的简谐力,并且忽略了管道振动对流体的作用,因此,计算结果与文献数据存在一定的差异(图5)。通过对比,本文的结果和文献结果在同一外部流体速度下的各点横向最大位移和振动形态基本一致,可证明采用Lamb-Oseen 涡模型进行模拟预测是可行的。
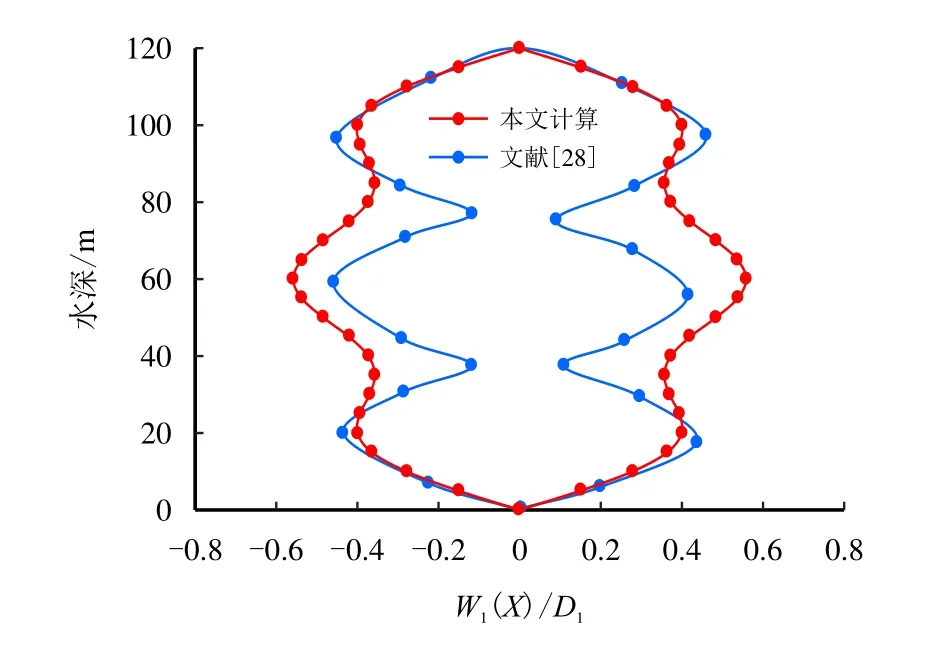
图5 PIP 系统位移响应验证Fig.5 Displacement response verification of PIP system
3.2 外部管道外径的影响
如图6 所示,表示外部管道外径对外激力的影响,且F1=F2=0,k=5×10−10GPa,c=0.059 N·s,ω′=0.2,忽略绝缘层质量。外激力计算采用Lamb-Oseen 涡模型,从文献[27]中可知,外激力恒大于零。从图6 中可以看出:当外部管道D1=0.26 m 时,在dr=2.0 m 时达到幅值;当外部管道D1=0.28 m时,在dr=2.6 m 时达到幅值;当外部管道D1=0.30 m时,在dr=3.2 m 时达到幅值;当外部管道D1=0.32 m时,在dr=3.8 m 时达到幅值;当外部管道D1=0.34 m时,在dr=4.6 m 时达到幅值。由此得出结论:外部管道外径越大,流体产生的外激力幅值越大,并且产生幅值的位置离管道越远。
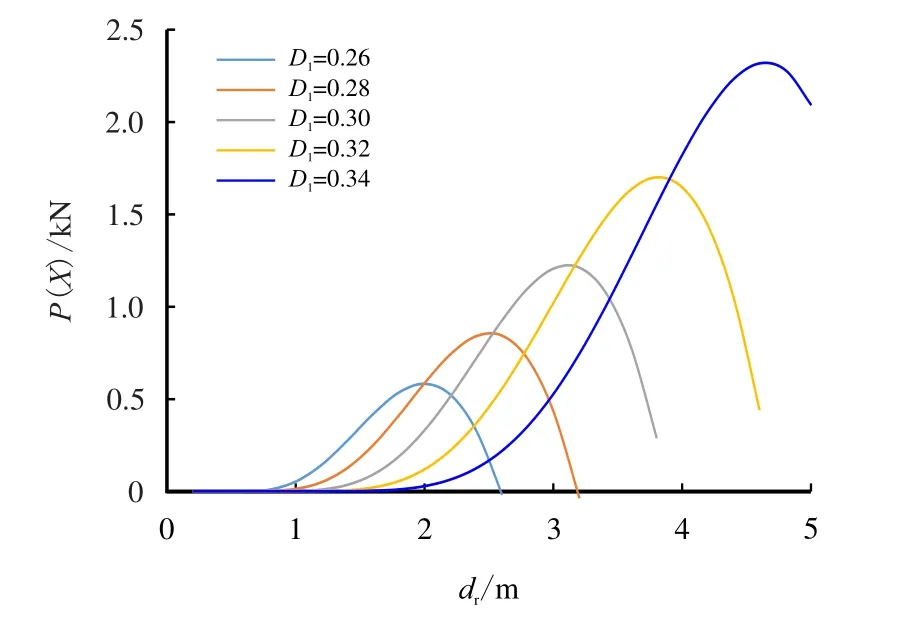
图6 外部管道外径对外激力的影响Fig.6 The influence of pipeline diameter on vortex induced force
图7 为外部管道外径对系统的影响。从图7可以看出,由于流速较小只能激发管道的一阶模态,即在X=0.5 处位移达到最大;在ω′不变的情况下,随着管道直径的增加,外部管道的响应也增加,内部管道的响应减小,内外管道的位移响应存在较大差距,所以管道直径不宜取太大,从而减小振动响应。
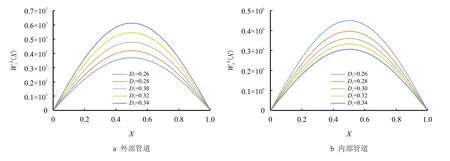
图7 外部管道外径对系统的影响Fig.7 Effect of pipe diameter on system
3.3 无因次轴向拉力的影响
图8 为不同无因次轴向拉力和管道模型位移响应的关系图,且F1=F2,c=0.059 N·s,ω′=0.2,k=5×10−10GPa。从图8 可以看出,当F′在0.2∼0.8变化时,外部管道位移逐渐增大,并且在0.6∼0.8 变化时位移变化幅度较大;内部管道受无因次轴向拉力的影响较小,位移响应变化较小,当F′=0.4 时,内部管道位移发生较大变化。
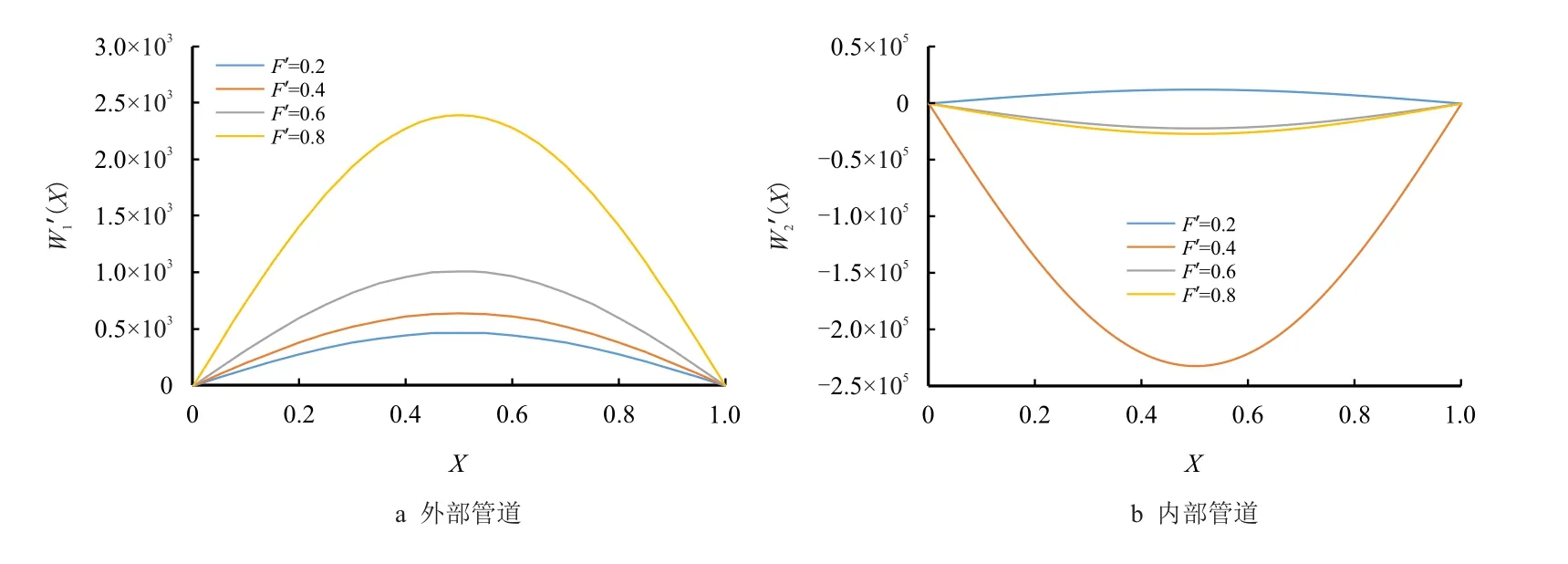
图8 不同无因次轴向拉力对应的管道位移响应图Fig.8 The response diagram of pipe displacement corresponding to different tensile forces
3.4 无因次频率的影响
流体速度发生改变时,作用在海洋立管上的外激力及频率发生改变,这会对管道模型的位移产生影响。从前面计算可知,流速和无因次频率成正相关。如图9 所示,绘制了无因次频率和外激力的关系图,在本算例中,k=5×10−10GPa,c=0.059 N·s。D1=0.26 m,L=3.9 m。
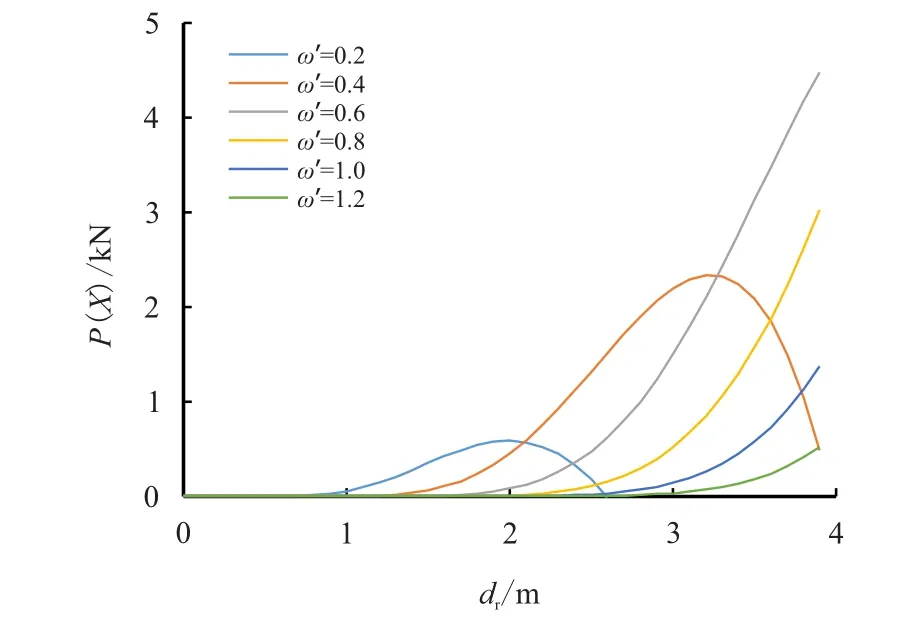
图9 无因次频率与外激力的关系图Fig.9 Diagram of dimensionless extraneous excitation frequency and vortex induced force
从图9 可以看出,当ω′=0.2 时,dr=2.0 m 时P(X)达到幅值;当ω′=0.4 时,dr=3.2 m 时P(X)达到幅值;当ω′≥0.6 时,dr=3.9 m 时P(X)达到幅值;当ω′=0.6时,P(X)达到最大幅值。由此得出结论:随着无因次频率的增大,外激力幅值先增大后减小,并且产生幅值的位置离管道越来越远。
图10 为无因次频率与外部管道位移的关系图,k=5×10−10GPa,c=0.059 N·s,F′=0.2。从图10可以看出,随无因次频率的增大,外部管道位移先增大后减小,在ω′=0.8 时发生反向。当ω′达到0.4时,外部管道位移超出允许变形范围极限,允许变化范围极限是中间绝缘层的厚度0.02 m,此时,可判断内外管壁发生周期碰撞,易对海洋立管造成损伤。
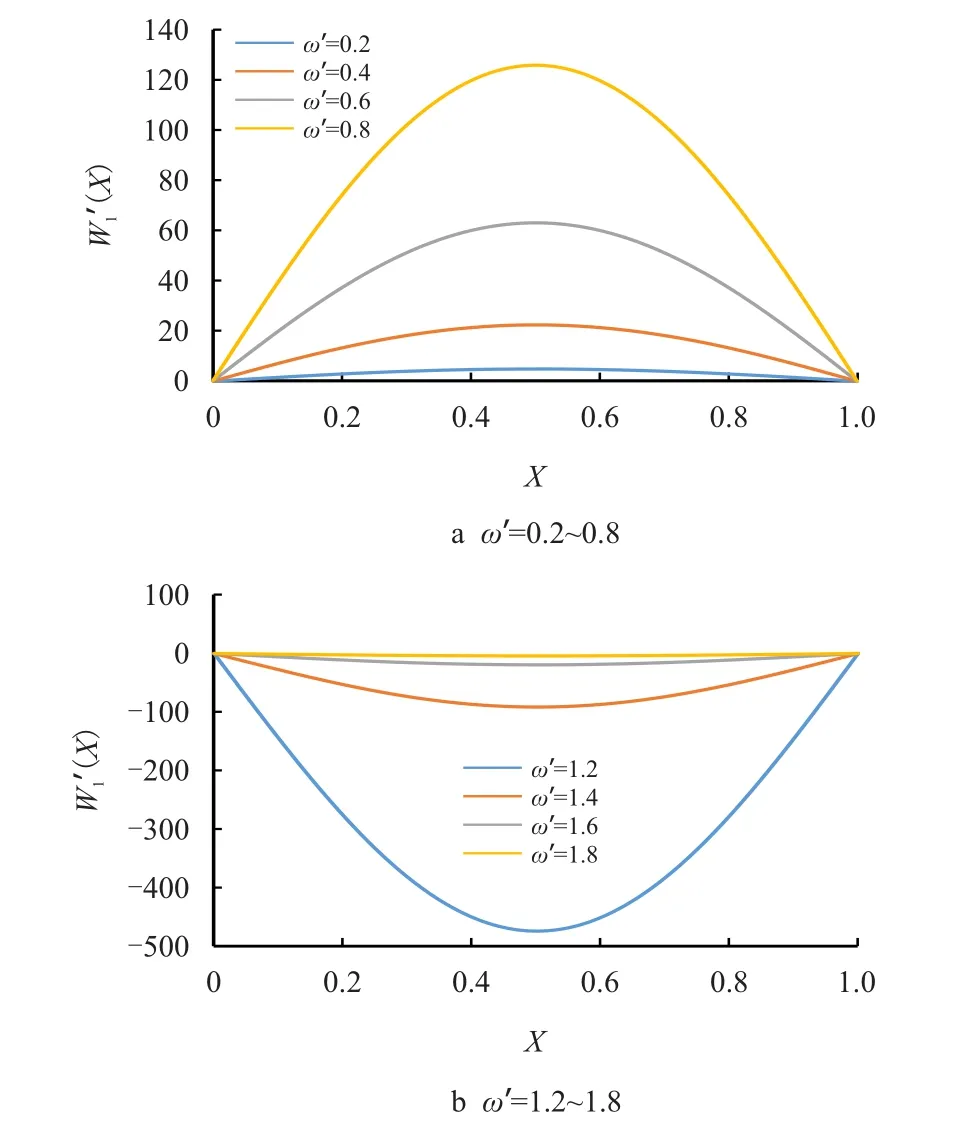
图10 无因次频率与外部管道位移响应图Fig.10 Diagram of dimensionless frequency and outer pipeline response
如图11 所示,绘制了无因次频率与内部管道位移的关系图,绝缘层弹性模量为5×10−10GPa,阻尼为0.059 N·s,无因次轴向拉力0.2。从图11 可以看出,随无因次频率的增大,内部管道位移先增大后减小,在ω′=0.6 时发生反向。相比于外部管道,内部管道的位移较小。
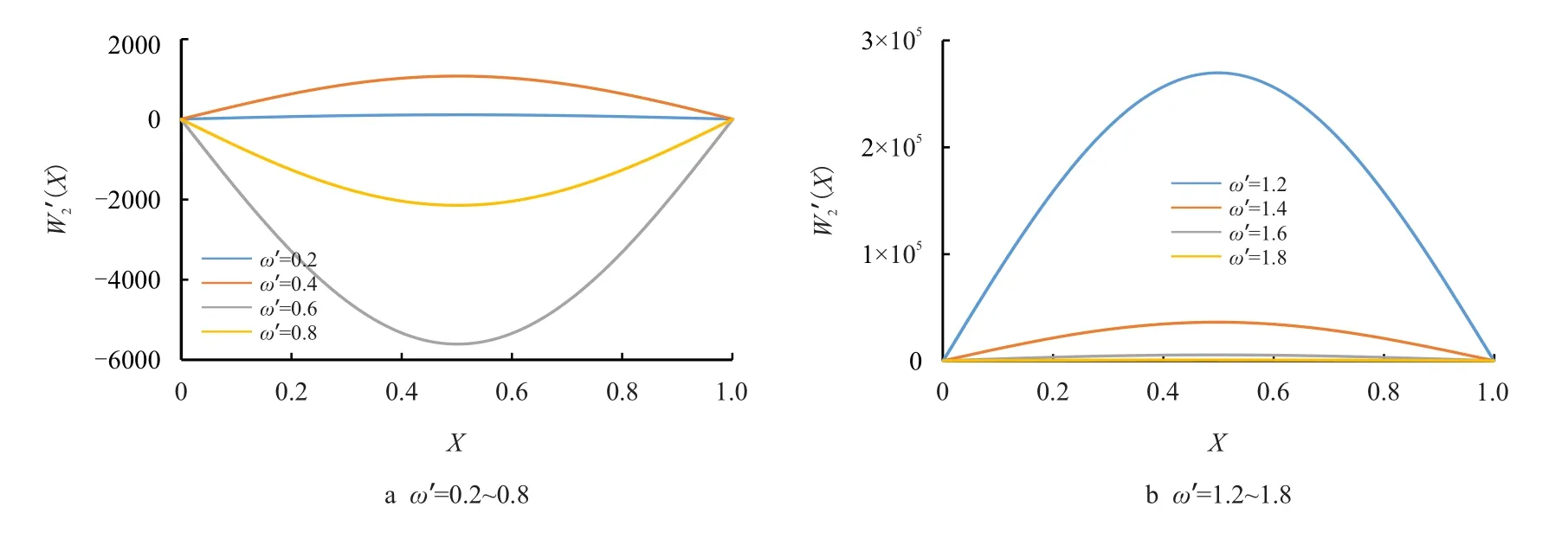
图11 无因次频率与内部管道响应的关系图Fig.11 Diagram of dimensionless frequency and inner pipeline response
随着无因次频率的继续增大,便会激发系统高阶模态。从图12 中可以看出,随着无因次频率的继续增加,外部管道和内部管道的位移越来越小。
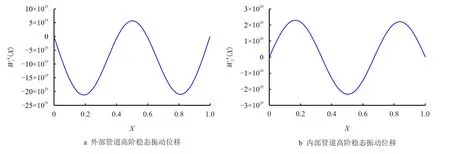
图12 无因次较大频率与管道系统响应的关系图Fig.12 Diagram of dimensionless higher frequency and piping system response
4 结论
1)在其他条件不变的情况下,管道直径增加,外激力增大,外激力产生最大幅值的位置远离管道,外部管道的振动响应增大,内部管道的振动响应减小。
2)轴向拉力的增加会增大外部管道的位移响应,影响较大,对内部管道的影响较小。
3)随着无因次频率的增大,外部管道和内部管道的位移都先增大后减小。无因次频率取0.4 时,外部管道位移超出允许变形极限,此时,可判断内外管壁发生周期碰撞,易对海洋立管造成损伤。
