超深井高温高压井筒复杂流动压力演变规律研究

2023-08-02邓虎，唐贵，张林

西南石油大学学报(自然科学版) 2023年4期

邓虎，唐贵，张林

川庆钻探工程有限公司钻采工程技术研究院，四川广汉618300

引言

开展超深井钻探作业时，井筒内流体状态是影响机械钻速快慢、钻井作业成败和钻井成本控制的关键。超深地层的高温使得井筒内流体性能难以保证，而高压使得井底压力控制更加困难，若控制不当就会造成气侵发生。超深井早期气侵监测非常困难[1]，当井口监测到气侵时，井底已连续侵入较多流体，井底压力持续降低，地层流体侵入井筒逐步加剧，如此恶性循环，增大了井控风险。因此，研究高温高压井筒复杂流动压力演变规律对超深井钻探作业的风险控制有十分重要的意义。

井筒瞬态多相流动规律及控制一直是油气勘探开发过程中的研究焦点之一。近年来，随着钻探井深的不断增加，又有了一些重要的研究成果。2015年，Meng 等基于Shi 漂移模型建立了环空两相流瞬态预测模型，在考虑井筒温度的情况下，建立了储层-井筒耦合瞬态多相流流动模型[2-3]。2017年，Yin 等提出了油基钻井液在深水钻井作业时，发生气侵条件下的井筒环空多相流动瞬态模型[4]。2018 年，Sun 等建立了考虑地层酸性气体侵入井筒后的相变及溶解的井筒多相流模型，并给出了此类多相流的流动摩阻系数计算方法[5]。同年，You 等建立了井筒蒸汽多相流动数学模型，并用于稠油注采时的井筒温度预测[6]。2019 年Fang 等考虑了地层渗流与井口控制，建立了地层-井筒-井口耦合的多相流瞬态流动精细模型，有效地分析了控压钻井过程中井筒瞬态流动特征，揭示了复杂多相流流动变化规律[7]。2022 年，Liao 等建立了包含水合物相变的气-液-固多相四组分井筒多相流动模型，为水合物储层中水平井钻井的井筒压力控制提供了理论及技术支持[8]。

目前的研究虽然从不同角度研究了井筒多相流的流动规律，但对于超深井的流动动态研究较少。超深井在高温高压作用下，气侵溢流时的两相流流动机理更为复杂，早期预警更为困难，若未及时采取有效措施，可能会造成严重后果。在前人的研究基础上，针对超深井高温高压井筒复杂流动特性，建立了一套超深井井筒地层-井筒耦合瞬态流动数学模型，基于AUSMV 格式的高精度数值求解方法进行求解，并利用现场案例分析了超深井高温高压井筒复杂流体压力瞬态演变规律，为超深井钻井过程中的井筒压力剖面预测提供了理论依据。

1 高温高压井筒复杂多相流动模型

1.1 气液两相流动的物理模型

1.1.1 物理模型概述

钻井过程中的井内水力学体系物理模型如图1所示。该体系包含两个流域[9]：1）井口至钻头底端的钻杆内圆管流域，通常是钻井液单相流动，对于充气钻井而言则是气液两相流动；2）钻头底端至井口的环空流域，气侵时为气液两相流动。井筒内可视为由不同截面积的流道串联而成，流道之间存在突变连接点。

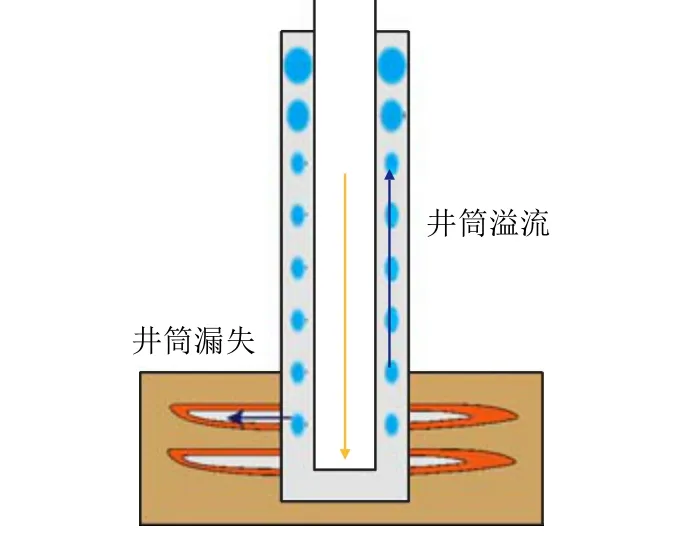
图1 超深井钻井井内水力学体系物理模型Fig.1 Physical model of hydraulic system in ultra-deep well drilling

1.1.2 基本假设

为降低超深井井筒气液两相瞬态流动问题求解的难度，在流动模型建立之前特作出如下假设：

1）将井筒中的钻井液、气体、岩屑多相流视为一维均质流动。

2）将井壁、套管及钻柱视为刚体。

3）不考虑钻柱的偏心。

4）不考虑钻井液流动过程中温度的瞬态变化，也不考虑侵入流体在井筒中可能发生的相变。

1.2 环空气液两相流动数学模型

基于以上的物理模型和基本假设，考虑气液两相间滑脱效应，建立超深井一维环空气液两相瞬态流动的控制方程

为使方程封闭，引入气液两相间的漂移关系式

由式（2）可知，确定气相漂移速度ud和气相分布系数C0之后即可确定气相的真实速度。对于传统的气液两相流计算，需划分气液两相流动流型，依赖于实验数据分析得到的经验系数C0，通用性不足。而漂移模型[10]计算结果连续，精度较高，经多次计算验证符合本文计算特征，故本文选用此模型。

此模型中需增加的辅助方程

对于超深井，流动摩阻与井深直接相关。为此，需选择合理的流动摩阻系数求解模型。本文选用基于混相流动的雷诺数摩阻模型[11]

计算地层气侵速率可采用非稳态储层气体渗流模型

在钻井期间，随着井深的增加，井筒环空压力也从低压不断升到高压，不同压力下气体压缩因子Z也不相同。结合文献[12-16]，得到不同压力梯度下的最佳压缩因子计算模型。

当pr<8 时，采用低压模型[12]

相对于其他流动机理模型，本文特别考虑超深井高温高压工况下的气体物性变化，构建更为精确的辅助参数模型，力求获得更为精确的计算结果。

2 复杂多相流动模型求解

多相流计算模型的计算方法选择对于计算精度与计算速度均有十分明显的影响。迎风型矢通量分裂格式（Advection Upstream Splitting Method，AUSM）最开始用于航空航天计算，后逐渐推广应用到其他领域[17]。其格式分裂形式简单，计算效率高，计算结果稳定，适用范围广，本文采用该模型进行求解。

将式（1）写成

气液两相流漂移模型包括气液两相运动，因此结合气相和液相运动，无黏通量矢量可写为

以单元界面xj+1/2为例，对无黏通量矢量进行离散以构造数值通量

应用上述模型可以计算出在超深井井筒气液两相流速与压力等参数的瞬态变化特性，其计算流程如图2 所示，从而预测超深井全井筒复杂流动压力、溢流量等参数的动态变化。

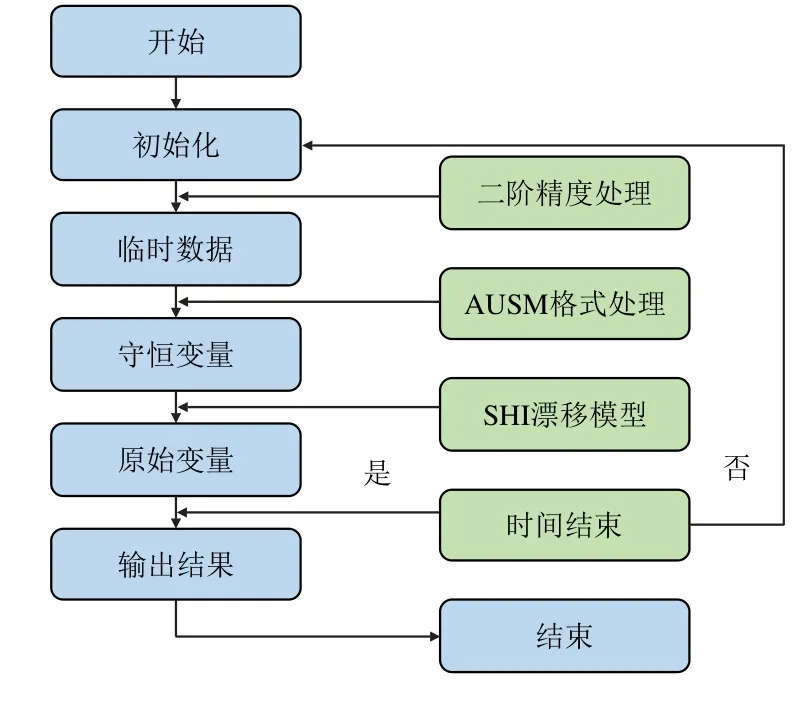
图2 瞬态计算流程图Fig.2 Transient calculation flow chart

3 高温高压井筒瞬态流动模型验证

通过建立的超深井全井筒复杂流动数学模型，基于AUSM 格式高精度数值求解方法计算超深井井筒气液两相瞬态流动及压力演变规律，从而可得出规律性的认识。这对研究超深井温度、压力变化条件下井筒压力演变规律和流动瞬态变化特征有积极意义。本文以ST8 井为例对数学模型进行验证。

ST8 井设计井深7 529.49 m，钻具组合如表1 所示，井身结构如图3 所示。以ST8 井7 400.00 m 时正常钻进工况进行模拟计算。此时，钻井液密度为1 550 kg/m3，塑性黏度为25 mPa·s，排量为17 L/s，井口回压为0.1 MPa。

表1 ST8 井7 400.00 m 时的钻具组合Tab.1 Drilling tool assembly of 7 400.00 m in Well ST8

查阅ST8 井井史得到立压分布，结合本文建立的模型进行计算。根据压力平衡守则，分析环空与钻柱内压力分布，以立管压力作为对比，如图4 所示。计算结果表明，本文所建模型的精度为94.7%，而采用传统的按照流型划分的模型计算精度为88.6%。本文建立的模型精度更高，可用于现场工程计算。

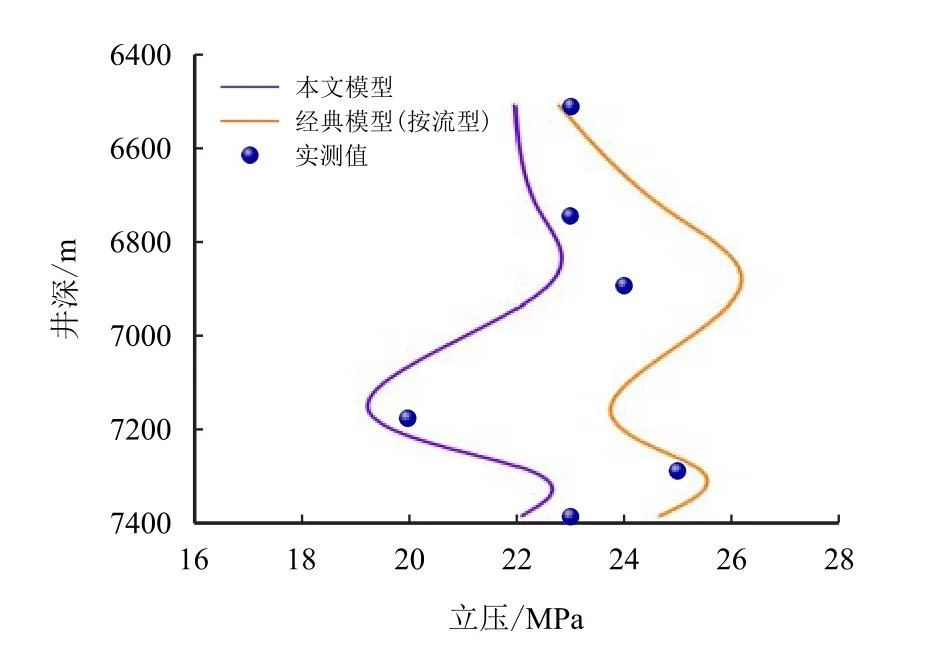
图4 立压计算结果与实测结果对比Fig.4 Comparison of vertical pressure calculation results and measured results

4 高温高压井筒瞬态流动规律计算

在钻井过程中会遇到地层流体侵入井筒，从而出现复杂井筒多相流情况，按出现气侵的类型可以分为单溢流和溢漏同存[18-25]。前者是因为地层压力高于井筒压力，而后者是因为窄密度窗口和存在溢漏窗口从而导致的复杂流动，其流动过程更为复杂。

4.1 单溢流和溢漏同存条件下的井筒流动规律对比分析

图5 是单溢流与溢漏同存条件下的井底压力对比。

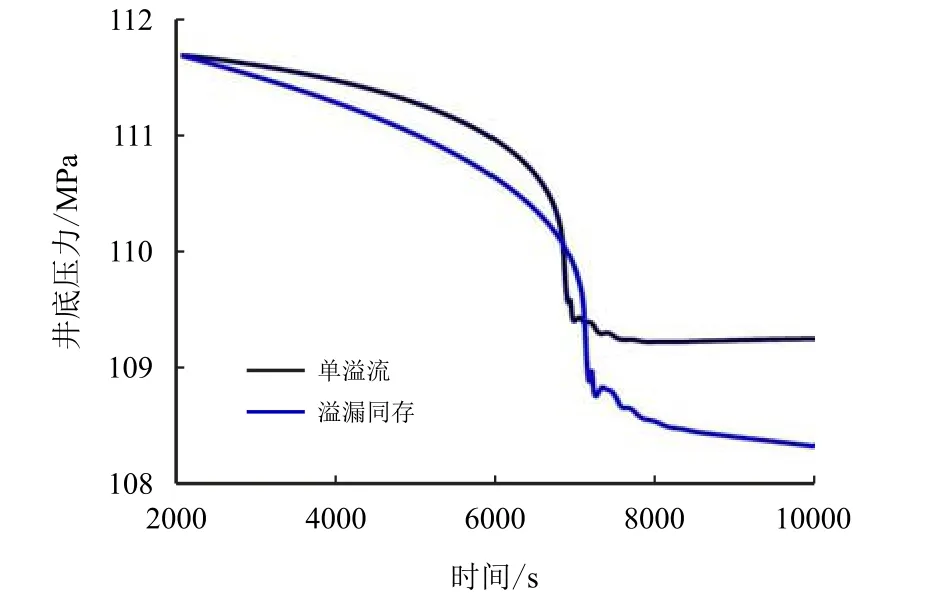
图5 单溢流与溢漏同井底压力存对比分析Fig.5 Comparison of BHP between overflow and coexistence conditions

在溢流初始时刻，两者压力保持一致，随着气体的侵入，井底压力开始下降，呈现先慢后快的趋势。溢漏同存由于存在漏失现象，降低了静液柱压力，压力下降更为迅速。同时，由于液体漏失，造成井筒有效排量降低，所以气体运移到井口的时间增加。液体漏失的部分造成井筒流体体积亏空，而气体膨胀造成流体体积增大，两者相互抵消，这给井口液量监测带来了严峻挑战。当在井口监测到气体溢流时，已造成井底压力较大幅度降低，后续由于持续气侵，压力继续降低，可能造成更为复杂的事故。

图6 为单溢流和溢漏同存条件下的压力剖面分布。钻柱压力入口处为立压，在钻铤变径处压力梯度开始减小，同时在钻头处有压力降，最后在井底与环空压力保持平衡。溢漏同存条件下在钻柱入口处的立压有明显变化，这是因为环空漏失施加了反向的摩阻，减小了压力损耗，所以立压也有所减小。

图6 单溢流和溢漏同存条件下的压力剖面分布Fig.6 Pressure profile distribution under overflow and coexistence conditions

图7 为单溢流条件下不同时间的环空压力剖面图。

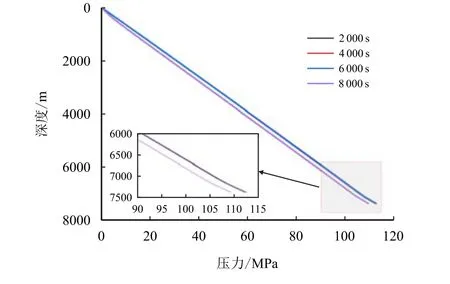
图7 不同时间下的环空压力剖面图（单溢流）Fig.7 Annulus pressure profile at different times(overflow)

与溢流前相比，在溢流2 000，4 000，6 000 和8 000 s 时，压力下降值分别为0.18，0.39，0.81 和2.45 MPa。气体刚开始侵入时，环空中的气体总量比较小，且主要集中在下部，同时由于高压压缩而体积较小，气体顶替液体量也比较小，压力下降较慢。当气体逐渐运移到井口时，气体加速膨胀造成液体被大量顶替从而引起环空压力明显变化，井底压力迅速降低，井筒与地层压差增大，导致更多气体进入井筒，如此恶性循环。因此，在实际操作过程中，早期气侵监测显得尤为重要，在情况出现恶化前采取有效措施避免更为复杂的事故。

4.2 不同密度下的井筒瞬态流动规律影响

钻井液的密度直接影响井筒内环空压力分布。在钻井工程设计中，需通过邻井压力剖面来设计合理的钻井液密度，以避免复杂情况。对于多压力地层，钻井液密度的选择更为重要。分析过程中分别采用了1 550，1 500 和1 450 kg/m3等3 种不同的钻井液密度。

图8 和图9 展示了采用不同钻井液密度及不同井下复杂流动条件下（单溢流、溢漏同存）的井底压力演变规律。

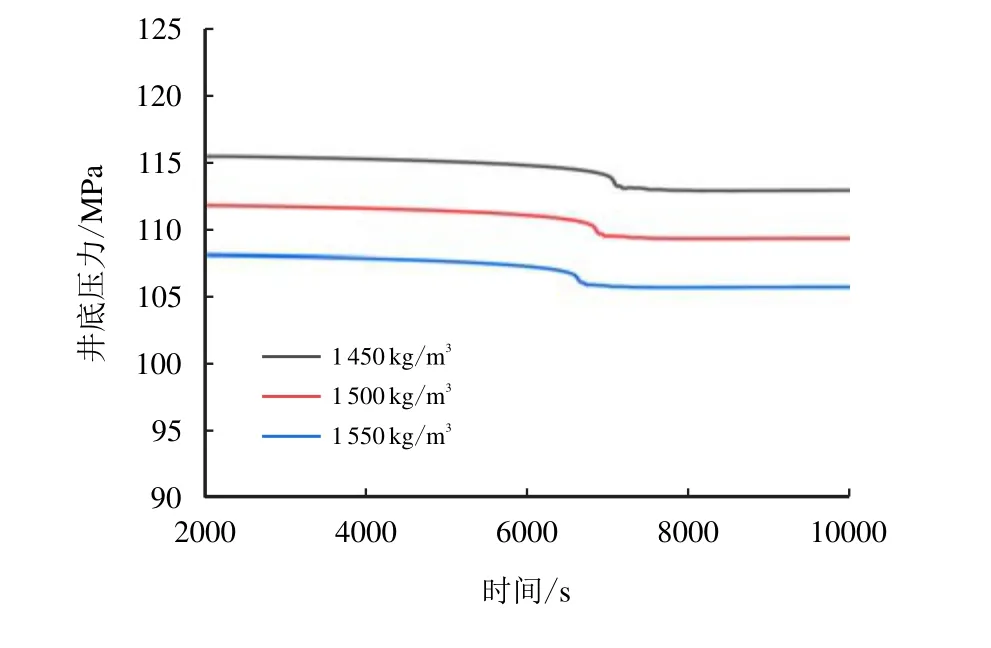
图8 单溢流条件下的井底压力分布Fig.8 Pressure distribution at the bottom of the wellbore under overflow conditions

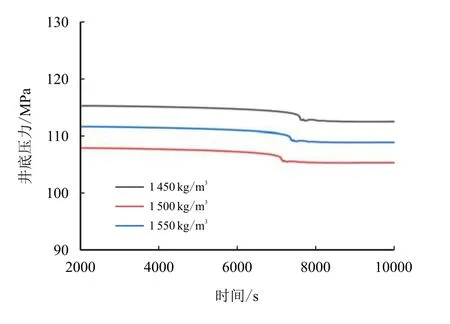
图9 溢漏同存条件下的井底压力分布Fig.9 Pressure distribution at the bottom of the wellbore under the condition of coexistence of overflow and leakage

图10 为单溢流条件下的压力剖面分布，环空连接大气压。由图10 可见，压力曲线近似直线，但在套管鞋处（7 093.00 m）环空压力梯度开始增大。

不同密度条件下的压力变化特征见表2，在单溢流时压力下降分别为2.52，2.45 和2.35 MPa；溢漏同存时，压力下降分别为2.76，2.69 和2.58 MPa。在相同钻井液密度下，溢漏同存的压力下降比单溢漏下降的幅度要高。钻井液密度的增加对改变井底压力的绝对值有明显影响，但压力下降幅度变化不明显。

表2 不同密度下的压力变化特征Tab.2 Characteristics of pressure changes under different densities

4.3 不同排量下的井筒瞬态流动规律

钻井液排量大小直接影响到井筒内气液两相分布，同时对井底压力亦有明显影响。排量越大，则附加流动摩阻越大，井底压力下降越小。

不同排量条件下的压力变化特征见表3。

表3 不同排量下的压力变化特征Tab.3 Pressure variation characteristics under different flow rates

由表3 可以看出，在23，20 和17 L/s 等3 种排量情况下，单溢流时压力下降分别为2.26，2.52 和2.67 MPa；溢漏同存时压力下降分别为2.35，2.66 和2.99 MPa。在相同排量下，溢漏同存的压力下降幅度明显比单溢漏下降的幅度更大。因此，提高钻井液排量，可以降低井底压力下降幅度。