误差集中策略的PID调参算法及联合仿真研究*
2023-08-02牟宗亮陈建华钟俊柏
牟宗亮,徐 雷,陈建华,钟俊柏
(四川大学机械工程学院,成都 610065)
0 引言
PID控制以其结构简单、易于实现等特性在控制系统中得到了广泛的应用[1]。经典的PID控制具有简单、成本低的优点,但难以快速准确地针对非线性和不确定的系统做出反应,起动特性弱[2-4]。目前,针对PID控制算法有进化算法寻找神经网络的最优初始连接权参数集以改善修正过程,也有利用模糊控制和模糊自整定策略的PID控制方法[5-7]。近些年来,国内外针对PID控制的参数选取和优化做了相应研究。李建伟等[8]提出了采用改进RBF神经网络进而优化PID控制。QIANG等[9]将神经网络动态修正策略应用于随机运动轨迹的控制过程。DAUD、ELSISI等[2,10]则通过使用多项式变异形成修正程序以优化PID控制参数并测试自适应PID控制。上述方案主要集中采用动态修正的策略,通过数学方法和神经网络等方法控制PID系统,相较于传统的PID控制方案在信号的最终稳定性上有很大提高,但是由于前期参数的选取没有足够的数据进行修正和测试,存在受被控系统影响大和动态修正过程中前期控制参数不良的情况。
针对上述问题,本文提出一种基于误差集中策略的神经网络PID改进算法。采用更加可靠的PID参数选取方案,剔除不良参数的影响,提出了一种误差集中反馈的创新训练模式。与上述方案相比,保证了控制过程中的每个控制参数都具有很好的控制性能。此外针对异常波动量进行的辨识和修正,极大地强化了针对复杂控制曲线的适应能力,面对复杂系统也能够快速、准确地进行修正控制。
1 传统调参修正策略
以BP神经网络为例,其主体结构由输入层、隐含层及输出层组成。将神经网络与PID控制相结合,则输出层体现为PID控制中的KP、KI和KD三个控制参数。而用于修正神经网络的反馈值则有PID控制器的控制结果提供。以传统思路为例,其控制的修正过程如图1所示。
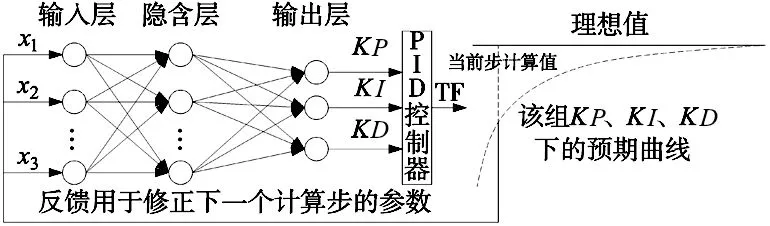
图1 传统修正过程
在该思路中,神经网络的输出层直接输出PID控制所需要的3个参数,即KP、KI、KD,参数在导入PID控制器后用于下一步的计算,现采用增量式PID,则当前计算点输出为:
yout(k)=yout(k-1)+Δu(k)
(1)
Δu(k)=KP[e(k)-e(k-1)]+KIe(k)+
KD[e(k)-2e(k-1)+e(k-2)]
(2)
在已有输出值的前提下,将误差反馈到神经网络的输入层,再次训练并修正神经网路的权值和阈值,之后生成新的PID参数,再次用于下一步的计算,即实现了参数的动态修正。
但是该方法存在两点问题:
(1)由于其训练集是由反馈的参数提供,故前几个控制步所使用的PID控制参数是在很少的训练集修正后得出的,所以其前段的控制结果并不理想。
(2)在整体上是利用神经网络修正出符合传递函数性质的权值和阈值,但是在局部上却以前一步的误差值修正后一步的控制参数。
2 改进调参修正策略
基于以上分析,本文采用采用误差集中的思想改进上述的神经网络—PID算法。具体结构如图2所示。
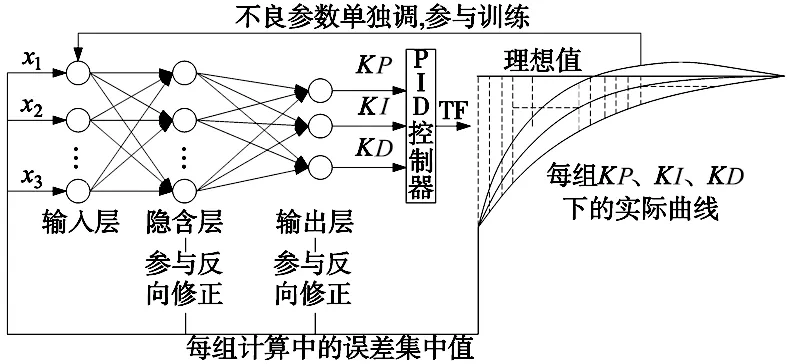
图2 改进后修正过程
本方法的基本思想是取代传统的反馈单个计算步误差的方案,在完整运行PID控制的前提下,取全部计算步的误差和代表该系统的整体特征进行反馈。在神经网络计算的内部算法上进行改进优化,使其能够针对误差和形式的反馈量进行有效训练,并强化其修正性能。
2.1 差分方程的转换
现将传递函数离散化后的方程形式表示如下:
(3)
式中:n与z分别代表分子分母部分的系数。根据以下换算关系:
z-nY(z)=y(k-n)
(4)
将式(3)交叉相乘并将式(4)带入变形后最终得到传递函数的差分形式如下:
y(k)=-d2y1-d3y2-d4y3+n1u0+n2u1+n3u2+n4u3
(5)
式中:u0、u1、u2、u3分别表示第k次、k-1次、k-2次、k-3次输入信号值,y同理。
2.2 误差集中方案
设定神经网络输入值为:
xi=[rin,yout,error,1]
(6)
式中:rin为期望值,yout为实际值,error为误差量,参与神经网络的正向传播获取PID控制参数K。将控制参数K带入式(1)和式(2)得到信号量,经式(5)得到实际值yout。取计算步数为m进行后续计算,将全部计算步误差进行集中。有:
(7)
式中:eh为误差和,考虑到控制的实际曲线并不总是在理想曲线之下,故取绝对值。在不考虑控制时间的前提下,m为无穷大量,误差集中量为无穷大量。事实上,该策略的神经网络修正后实现的是误差和的缩小,即使选取的是局部的误差和,其也符合修正曲线的目的。故定义限制量mm及MM。有:
m∈[mm,MM]
(8)
式中:mm的选取不宜过小,与误差收敛速度相关,MM的选取与系统要求的最大控制时长相关。
在反向修正过程中,联接权值的改变量应为:
(9)
式中:α在该系统中定义为KP、KI、KD的系数矩阵,在误差集中策略中选取中段计算过程的系数能够达到较好的修正结果。K为影响修正速度的系数,变动后对修正速度有影响。取输出层激活函数ω2为:
(10)
隐藏层的修正同理,取隐藏层修正函数ω1为:
(11)
在获得权值改变量后对原权值进行修正,之后完成一次神经网络的训练。相较于传统的训练策略,该方案的神经网络训练次数不再受限于PID控制器的计算步数。其训练集来源既体现传递函数性质,又剔除了前期训练的不良样本。
在完成修正后,根据被控对象不同可能会有信号跟踪曲线呈现出很强的波动特性的现象,本文通过对这些异常信号辨识后进行局部修正,使信号整体稳定。
具体方法为通过式(1)的计算过程中,直接读取其实际值yout(k),则应有:
yout-rin≤ε
(12)
式中:yout为实际值,rin为理想值,ε根据系统允许的波动量选取,其值为正。在波动量超过ε时,则重新进行训练过程。在重新训练之前,需要剔除因波动造成的不良修正量。故进行修正如下:
(13)
式中:i为达到预期波动量前的修正次数。在达到可接受的波动量后,再重新计算全部计算步的实际值yout,重新进行误差集中及修正。
以某液压系统为对象对该算法进行验证,首先建立该液压系统传递函数如下:
(14)
式中:s为复变量,传递函数G(s)为s的有理分式,只取决于系统的结构和参数。取训练前参数与训练后参数分别测试控制效果,其结果如图3所示。
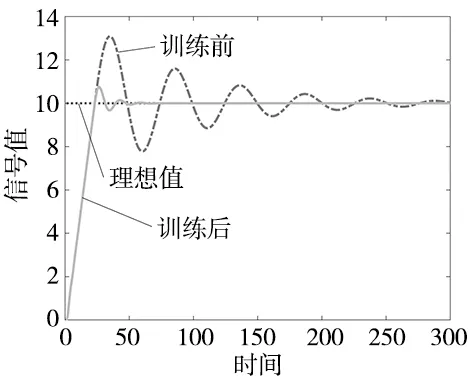
图3 训练前后信号跟踪效果对比
由图3可以看出,针对该传递函数本文算法有较好的修正效果,修正后得到的信号跟踪曲线在响应的快速性和稳定性上均有很大的改善。
3 MATLAB-Simulink-AMEsim联合仿真实例
为了验证上述算法的实际控制结果,本文以液压系统模型代替传递函数,避免了简单的传递函数过于理想化的情况,使仿真结果更加接近于实际情况,基于MATLAB-Simulink-AMEsim构建了一个联合仿真平台。
联合仿真平台的逻辑如图4所示。控制信号传输由MATLAB计算PID的控制参数并输入到Simulink,由Simulink计算最终控制信号输出至AMEsim建立的液压系统模型当中,最终执行机构实现位移。

图4 联合仿真平台逻辑图
反馈信号传输由Simulink将计算过程中的控制量及部分中间过程量反馈至MATLAB,AMEsim将液压系统模型的实际控制结果同步反馈至MATLAB,MATLAB进行计算并修正控制参数。
首先在AMEsim建立了一个液压系统模型如图5所示。
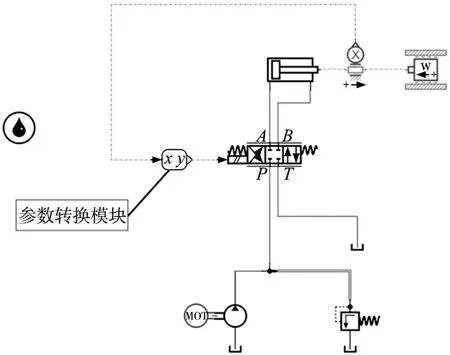
图5 液压系统模型
取负载块质量为100 kg,无初始速度及初始加速度,液压缸中引入摩擦以及内泄漏等不可控量,针对电磁换向阀也引入了合适的振动频率,保证模型的可靠性。模型的参数转换模块中导入训练计算过程,可将结果转化为控制信号直接作用于电磁换向阀,用于直接控制流量。位移传感器实时反馈液压推杆位移量,同样通过参数转换模块反馈至Simulink。Simulink完成PID控制的计算过程,Simulink系统模型如图6所示。
其中图6左边的部分接收经MATLAB修正计算得到的PID控制参数并通过式(1)、式(2)进行计算,其计算结果为最终控制信号。同时将计算过程中部分中间过程量反馈至MATLAB用于修正计算。图6右边的部分建立与AMEsim的联接,将最终控制信号传输到AMEsim中的液压系统模型中控制电磁换向阀,同时接收来自于液压系统模型中执行机构的当前实际位移量,并同样将数据传输至MATLAB用于修正计算。
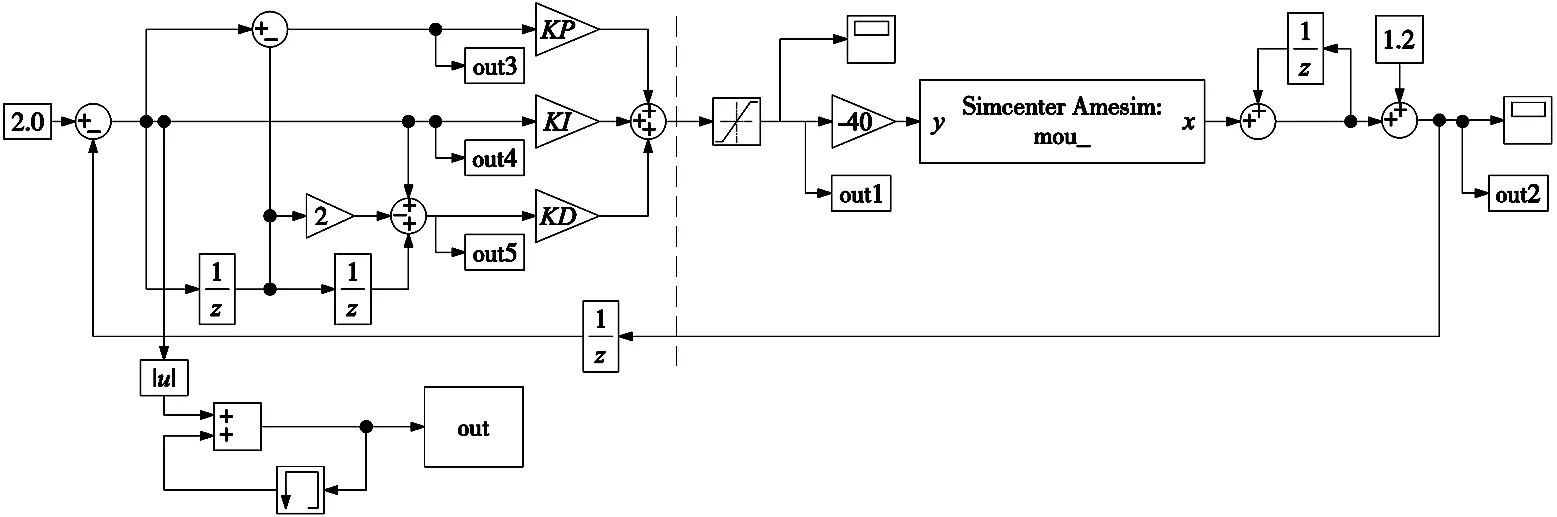
图6 Simulink系统模型
使用该液压系统模型将传统的神经网络调参修正算法与本文所述的改进算法进行仿真对比。现分别设定0.9、1.5、1.3以及2.0的预期值,采用两种算法进行仿真实验,其结果如图7所示。各种算法在仿真情况下的实际位移值见图中标注。
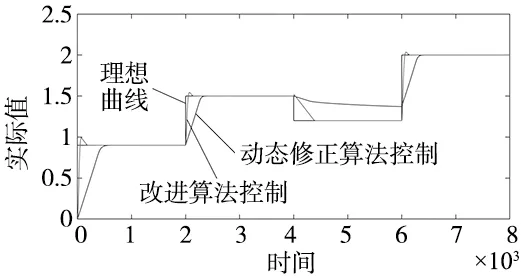
图7 仿真实验结果
根据仿真结果,本文所述改进算法相较于传统的神经网络动态修正算法在响应的快速性和最终响应的准确性上均有所提高。尤其在预期值小于当前值的负值误差修正阶段,改进算法依然能够快速地响应到设定值。
4 结论
针对PID控制器参数选择的不确定性问题,本文设计了一种针对神经网络的修正策略,采用控制过程中的误差集中方式,设计了局部阈值方案,最终得出以下结论:
(1)该策略利用全控制过程的数据进行计算,有效地提高了控制信号前期的响应速度,降低了信号的超调量,在极短响应时间内快速地应对随机误差量,使系统快速趋向稳定;设计大波动控制参数的局部调节方案,极大地提高了算法对复杂系统的调节能力。
(2)经MATLAB-Simulink-AMEsim联合仿真与传统动态修正算法进行对比,结果表明,该算法控制的响应速度和最终稳定性均有提高,针对变化信号的响应准确率也有所增加。
