基于电磁耦合结构的谐振屏蔽及抗偏移性能研究

吉 莉, 葛富辰, 张 弛, 张 明, 钱步仁, 孙红军

(中国石油大学(北京)信息科学与工程学院, 北京 102249)

1 引言

随着电动汽车充电技术不断创新,无线电能传输(Wireless Power Transfer, WPT)有效解决了有线充电方式需要电缆、难以在潮湿环境下充电等问题,使得电动汽车充电更加方便、安全、经济[1-3]。在无线电能传输技术中,目前应用最为广泛的是电磁谐振式WPT。其本质是利用一次回路线圈产生交变磁场,耦合至二次回路线圈,将电能传递给负载,实现为电动汽车充电[4]。由于磁场频率较高,根据SAE J2954规定,一般将电动汽车无线充电的频率设置为85 kHz[5],因此在充电过程中,会有一部分磁通量由WPT系统泄露到空气中,在车体周围产生漏磁场,形成的电磁辐射会对一些电子设备以及人体造成不利影响。

根据国际非电离辐射防护委员会(the International Commission for Non-Ionizing Radiation Protection,ICNIRP)制定的标准[6,7],磁感应强度的公众暴露限值是6.25 μT,而我国对电磁辐射限值更加严格,即需要小于1.4 μT。并且还在逐步加强管控,因此在电动汽车无线充电过程中削弱电磁辐射对人体的有害影响是一项关键课题。

国内外研究团队针对电磁辐射问题提出了如下解决方法:新西兰奥克兰大学提出基于圆形耦合线圈的铁氧体屏蔽方法[8-10],将铁氧体条在线圈表面均匀摆放。由于铁氧体具有较高的磁导率,可以引导磁通量靠近磁场源,从而减少周围的泄漏磁场。但是过多的铁氧体会降低系统的材料利用率。韩国科学技术院提出一种利用金属材料屏蔽电磁场的方法[11-13]。金属材料具有良好的导电性能,暴露在时变磁场下会感应出电流、产生反向磁场,进而抵消入射磁场,达到屏蔽的效果。然而金属屏蔽会导致线圈自感互感降低、有效串联电阻增加。中国科学院电工研究所提出了一种有源线圈屏蔽的方法[14-16],通过额外添加一个电源,主动调节屏蔽线圈的电流大小,使其产生一个与发射磁场大小相等、方向相反的磁场,消除泄漏磁场。不过在实验中使用有源组件,需要同时对屏蔽电流的振幅和相位进行控制,所以很难通过设计实现。针对有源屏蔽法的缺陷,韩国科学技术院提出了一种无功谐振屏蔽方法[17-20],该方法没有使用额外电源,通过WPT系统线圈产生的发射磁场穿过屏蔽线圈,从而产生一个屏蔽磁场,达到消磁目的,但是其没有考虑线圈偏移情况对系统性能的影响。

然而,在实际应用中WPT系统耦合结构偏移是不可避免的,容易出现横向、纵向的偏移,造成互感等参数改变、传输效率下降、稳定性降低等问题[21,22]。从当前的研究成果来看,大部分的磁屏蔽方法仅单一地考虑了消磁效果,忽略了耦合结构的抗偏移性能。如何在满足漏磁屏蔽的条件下,提高耦合线圈的抗偏移性能成为研究课题的关键。

本文将谐振屏蔽法运用在圆形线圈上,在达到减弱泄漏磁场目的的同时,对圆形屏蔽线圈进行分析设计,提高了线圈的抗偏移性能。具体而言,本文以WPT系统的耦合结构为研究对象,首先建立了系统的等效电路模型,推导出存在屏蔽线圈时系统的传输效率,并对谐振屏蔽的原理进行理论分析。主要通过屏蔽线圈的匝间距设计提升磁场均匀度,加强耦合结构抗偏移性能。然后采用Comsol软件进行有限元分析,以屏蔽线圈的匝数及位置、屏蔽电流为变量,设计了一套电磁屏蔽装置,同时与仿真对比,证明该装置具有良好屏蔽效果的同时,提高了耦合结构的抗偏移性能。最后搭建了WPT系统,通过LCR分析仪成功验证了屏蔽的有效性。

2 WPT谐振屏蔽及抗偏移研究

图1是一个利用戴维宁定理进行化简的具有屏蔽线圈的无线充电系统等效电路图。发射侧电路由等效的交流电压源U、发射补偿电容Ct、发射线圈自感Lt以及内阻Rt组成;接收侧电路由等效负载R、接收补偿电容Cr、接收线圈自感Lr以及内阻Rr组成;屏蔽侧电路由屏蔽线圈自感Lsh、屏蔽线圈内阻Rsh、屏蔽线圈的补偿电容Csh构成。图1中Mtsh为发射线圈与屏蔽线圈的互感;Mtr为发射线圈与接收线圈之间的互感;Mrsh为接收线圈和屏蔽线圈间的互感。

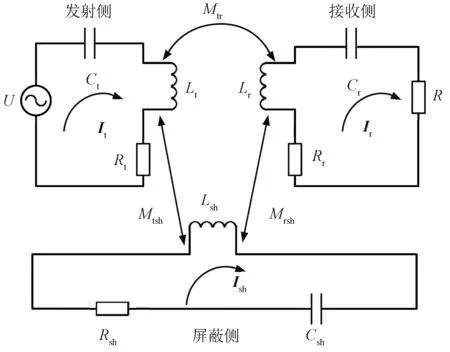
图1 带有屏蔽线圈简化无线充电系统等效电路图Fig.1 Equivalent circuit diagram of simplified wireless charging system with shielded coil

将流过发射线圈、接收线圈、屏蔽线圈的电流分别定义为It、Ir、Ish,由基尔霍夫电压定律可得:

(1)

(2)

(3)

式中,ω为角频率,并且ω=2πf。当1/(jωCt)+(jωLt)=1/(jωCr)+jωLr=1/(jωCsh)+jωLsh=0时,系统发生谐振,对式(1)～式(3)进行简化计算,由此可以推导出发射电流It、接收电流Ir、以及屏蔽电流Ish如式(4)～式(6)所示。

(4)

(5)

(6)

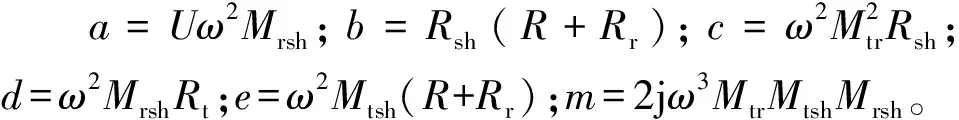
(7)

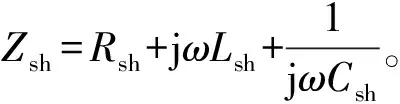
本文提出的谐振屏蔽是以泄漏磁场为来源产生屏蔽磁场达到磁屏蔽目的。与主动屏蔽、非谐振屏蔽、金属屏蔽等屏蔽方式相比,谐振屏蔽通过调节屏蔽线圈上的匹配电容控制屏蔽线圈电流的参数,进而控制屏蔽磁场的大小和方向。

图2是由谐振屏蔽法产生的磁场截面图。在无屏蔽措施的条件下,耦合线圈周围空间的磁场由图2中带有箭头的实线表示,它是由发射线圈和接收线圈决定的。将屏蔽线圈放置在与收、发线圈同一水平高度位置处,当耦合线圈的磁场穿过屏蔽线圈时,产生的屏蔽磁场受匹配电容调节与发射磁场方向相反,如图2中带箭头的虚线部分所示,对区域内的泄漏磁场产生屏蔽作用。

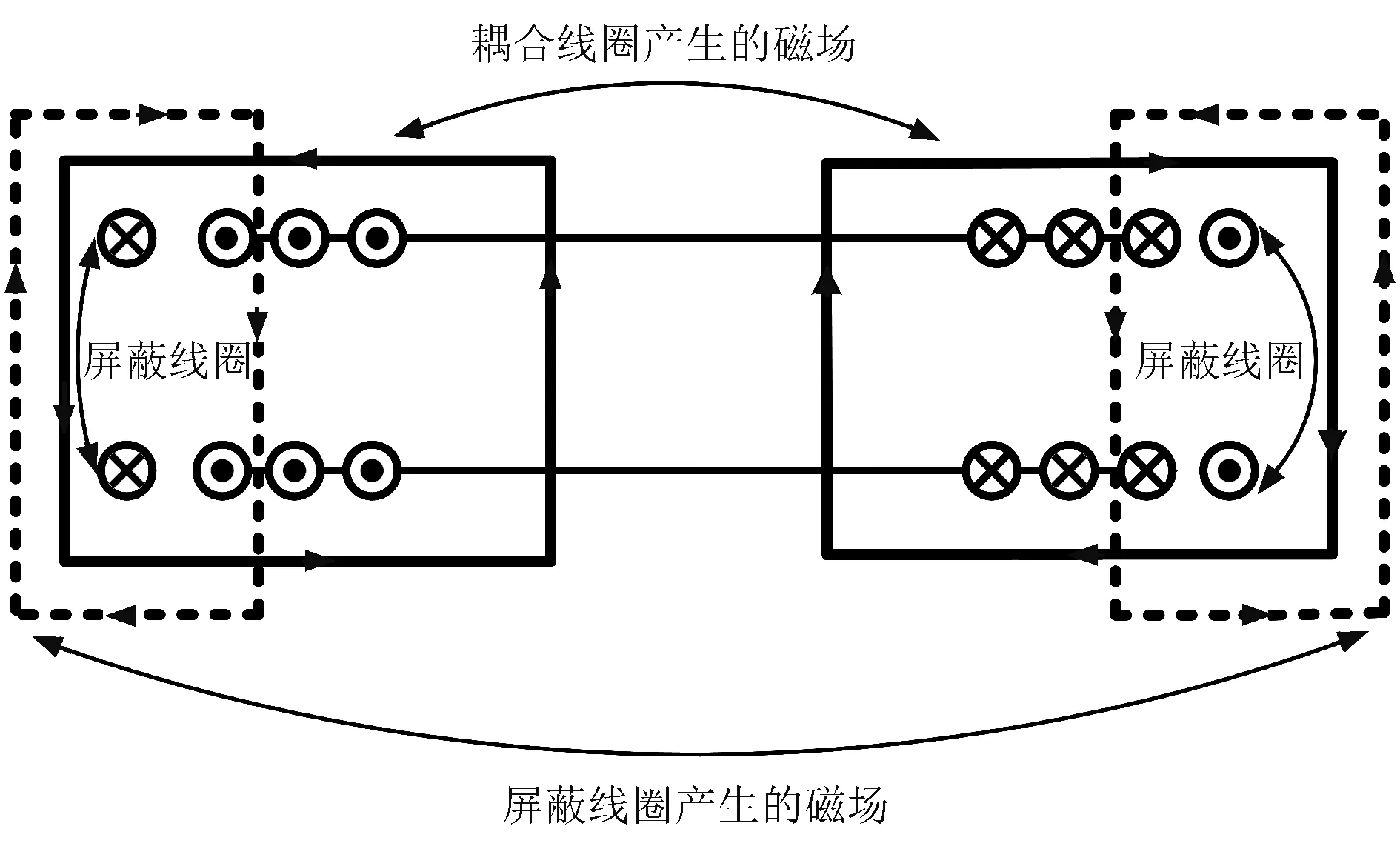
图2 谐振屏蔽概念图Fig.2 Concept diagram of resonance shielding

根据电磁感应原理,回路完整屏蔽线圈产生的感应电压Vsh如式(8)所示。

(8)

式中,φ为穿过屏蔽线圈的磁通量;S为屏蔽线圈的回路面积;Bt为发射线圈产生的发射磁场的磁感应强度。

调节电容器匹配,令屏蔽线圈的电流与发射线圈的电流相位相反,屏蔽电流Ish如式(9)所示。由电生磁原理,屏蔽电流产生的屏蔽磁场如式(10)所示。

(9)

(10)

式中,μ0为真空磁导率;Idl为电流微元;y为空间任意一点到导线的距离模长;Bsh为屏蔽磁场的磁感应强度;ay为y的单位矢量。

由于屏蔽回路阻抗是决定屏蔽性能的关键因素,所以用屏蔽电容来确定屏蔽回路的工作状态。当屏蔽回路的电容大于电感,回路处于容性状态时,式(9)变为式(11):

(11)

式中,Ceq为屏蔽回路的等效电容,由于Rsh为屏蔽线圈内阻,其阻值太小,故可以忽略不计[23]。

由式(11)可以看出屏蔽电流与原电流具有相同的相位,继而屏蔽磁场与原磁场相位也相同,所以该电流产生的磁场起到加强漏磁的作用。

当回路的电感大于电容,屏蔽回路呈现感性状态时,式(9)变为式(12):

(12)

式中,Leq为屏蔽回路的等效电感,内阻Rsh忽略不计。由式(12)看出屏蔽电流与原电流相位相反,使得屏蔽磁场与原磁场相位也相反,因此该电流产生的磁场起到屏蔽作用。

将屏蔽电感与屏蔽电容等效为式(13)中的等效电感Leq,计算得屏蔽磁场的磁感应强度Bsh如式(14)所示,r1～rN表示N匝屏蔽线圈的半径。

(13)

(14)

由于磁感应强度B是矢量,满足叠加定理,为实现耦合结构功率传递最大化,It与Ir的相位差是90°。如图3所示,无屏蔽条件下的总磁场可以表示为发射磁场与接收磁场的矢量和,如式(15)所示。

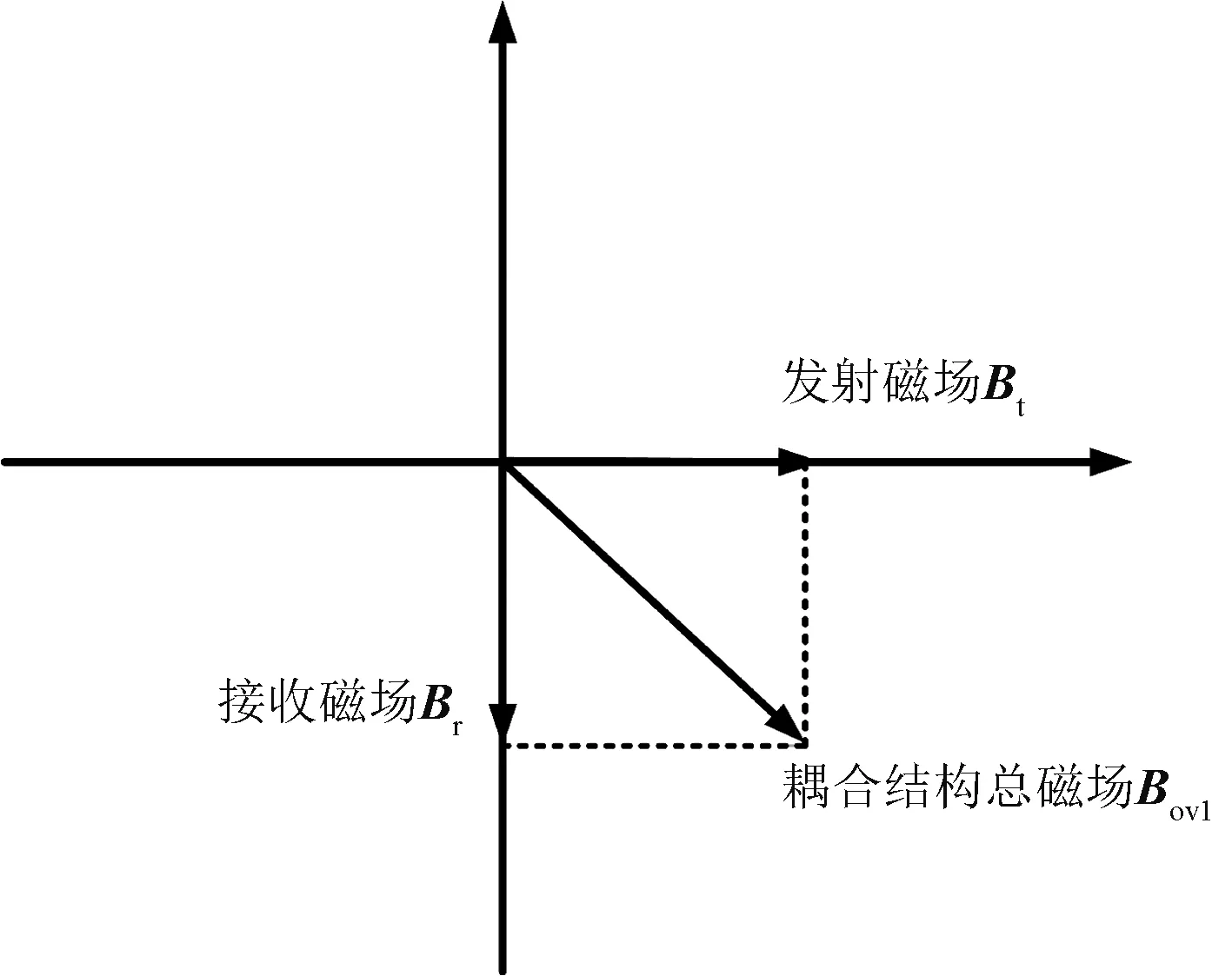
图3 无屏蔽线圈的总磁场Fig.3 Total magnetic field of unshielded coil

Bov1=Bt+Br

(15)

式中,Bov1为无屏蔽的耦合结构总磁场磁感应强度;Br为接收磁场的磁感应强度。

在耦合结构中添加屏蔽线圈后,WPT系统的总磁场由It、Ir及Ish共同决定,如图4所示,其中Bov为有屏蔽的耦合结构总磁场磁感应强度。

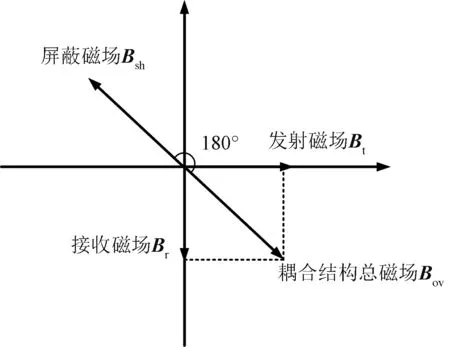
图4 有屏蔽线圈的总磁场Fig.4 Total magnetic field with shielded coil

对比图3和图4可知,在放置屏蔽线圈情况下,总磁场如下所示。

Bov=Bt+Br+Bsh

(16)

综合式(14)和式(16)可以得知Bsh与屏蔽电流Ish和屏蔽线圈匝数N相关。因此在耦合结构磁屏蔽设计上需要重点对Ish和N进行分析。在满足磁屏蔽要求下,为提高耦合结构的抗偏移能力,本文通过设计屏蔽线圈的匝间距离,平衡耦合结构的中间部分与边缘部分磁感线,提高系统的抗偏移能力。

综上所述,为了产生最佳屏蔽效果,通过改变屏蔽回路阻抗控制屏蔽电流大小,将其限制在对耦合结构周围的磁场起屏蔽作用的范围内。调节屏蔽线圈匝数以及其所处位置,令总磁感应强度Bov幅值达到最小,并与铁氧体屏蔽法进行比较,突出谐振屏蔽的有效性。保证在添加屏蔽线圈后能够有效提升磁场的均匀度,增强系统抗偏移性能,这就是本文研究设计的磁屏蔽结构。

3 仿真研究

图5为耦合结构的设计拓扑图,其中发射线圈、接收线圈以及屏蔽线圈皆采用简单的圆形线圈,屏蔽线圈设计为内疏外密的闭合结构。本文设定接收线圈最大直径为246 mm,为了便于进行实验分析,对收发线圈采用相同的设计参数,并将收发线圈对称放置,彼此之间的空气间隙为100 mm,系统工作频率为85 kHz。屏蔽线圈设定为3匝,其线圈半径分别为140 mm、150 mm、154 mm,放置在发射线圈周围。通过控制屏蔽电流、调节屏蔽线圈匝数以及其所处位置,确定最佳谐振屏蔽效果。

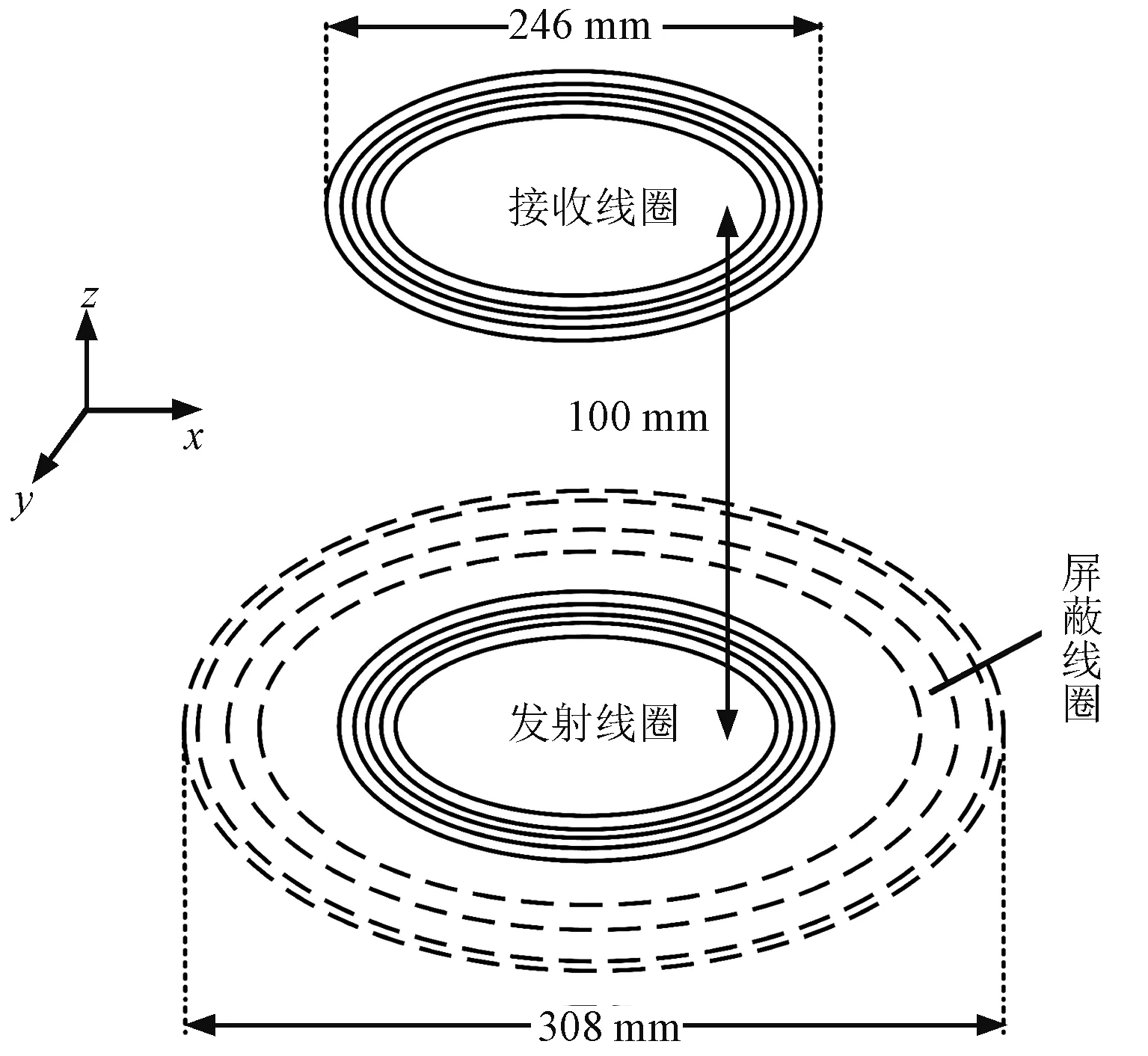
图5 带有屏蔽线圈的耦合结构模型图Fig.5 Coupling structure model diagram with shielding coil

3.1 屏蔽电流优化仿真

本文实验通过Comsol有限元仿真软件进行仿真,验证Ish对屏蔽效果的影响。首先固定3匝屏蔽线圈,通过调节Ish控制屏蔽磁场,并与无屏蔽时耦合结构周围磁场进行比较。表1为不同Ish时观察点处的总磁感应强度值。

表1 不同屏蔽电流观察点处的总磁感应强度值Tab.1 Total magnetic induction at the observation point at different shielding currents

由于耦合结构周围漏磁对人体的危害主要是x、y方向的磁场,所以本文设计圆形线圈且对称放置,y方向与x方向的磁屏蔽完全相同,故只需讨论x方向。为了明显分析对比,需要选定一个起始观察点,该位置不宜距离线圈过近,因为线圈所在的位置磁场较大。也不宜离线圈过远,因为磁屏蔽效果不明显。故本文选定空间中x坐标为220 mm作为起始观察点,仿真测量得到不同Ish时该点的总磁感应强度。

从表1中数据可得,当没有添加屏蔽线圈时,耦合结构在该点产生的总磁感应强度只受到发射线圈和接收线圈的磁场影响,其值为5.85 μT,当Ish增大到1.4 A时,也就是Ish与It的幅值比为1.4时,观察点的总磁感应强度达到最小值0.21 μT,计算出最大屏蔽差值为5.64 μT。

图6是一条在观察点处的Bov与Ish幅值的关系曲线,通过图6可知当Ish由0 A增加到1.4 A,该点的Bov呈现减小趋势。因为耦合结构在该点的磁感应强度不变,Ish增大,屏蔽磁场增强,由式(15)、式(16)可以推论出总的磁感应强度会减小。当Ish从1.4 A继续增大时,Bov呈现增大趋势,磁场屏蔽效果变差。根据第2节分析可知磁感应强度B是矢量,当Bsh>Bt时,增大Bsh值,总的磁感应强度Bov与Bsh方向相同,幅值增大,因此继续增大Ish值,会使Bsh持续增大,对磁场屏蔽造成消极影响。

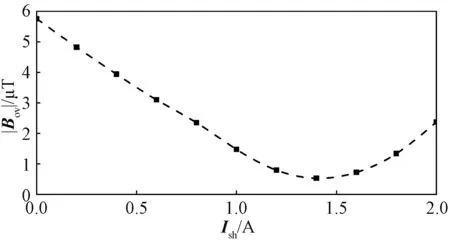
图6 观察点磁感应强度随屏蔽电流幅值变化曲线图Fig.6 Variation curve of magnetic induction intensity with shielding current amplitude at observation point

选择起始观察点以外的区域,通过仿真实验,将Ish从0.8 A到1.6 A分别对应的磁感应强度值绘制如图7所示。其中点虚线标注的1.4 μT代表国家规定的安全标准。观察到Ish等于1.4 A时,曲线数值较低,且变化较平缓,磁屏蔽达到最优效果。因此在固定其他参数不变的情况下,Ish与It幅值比为1.4,可以达到最佳的磁感应强度屏蔽效果。

根据上述仿真结果,结合第2节的理论分析可知Ish是有限定值的,磁场屏蔽效果不会随着屏蔽电流的增大呈现单调增强的趋势。由于Bsh与Bt方向相反,Ish较小时反向的Bsh较弱,可以起到减小Bt的作用,但随着Ish增大,会出现一个限定值K,使得该电流下的Bsh幅值与Bt幅值相等,方向相反,Bov减小到0。此时,继续增大Ish,就会造成Bsh大于Bt,对某一点的总磁感应强度起到反向增强的作用。因此当Ish小于限定值K时,Ish越大,产生的屏蔽效果就越好,而一旦屏蔽电流Ish超过K时,磁场抵消后会产生反向电磁场,此时Ish越大,产生的屏蔽效果就越差。

3.2 屏蔽线圈匝数、位置优化仿真

通过对屏蔽电流的优化分析,固定屏蔽电流Ish为1.4 A,仿真分析不同的屏蔽线圈匝数N情况下,屏蔽线圈所处不同的z轴高度对磁屏蔽性能的影响。在线圈匝数N分别取1、2、3、4条件下,线圈所处不同高度位置的磁感应强度值见表2。观察表2中数据,可得当屏蔽线圈所处z轴高度为0时,也就是屏蔽线圈与发射线圈处于同一水平高度位置,屏蔽线圈匝数N为3时,观察点处的磁感应强度最小。

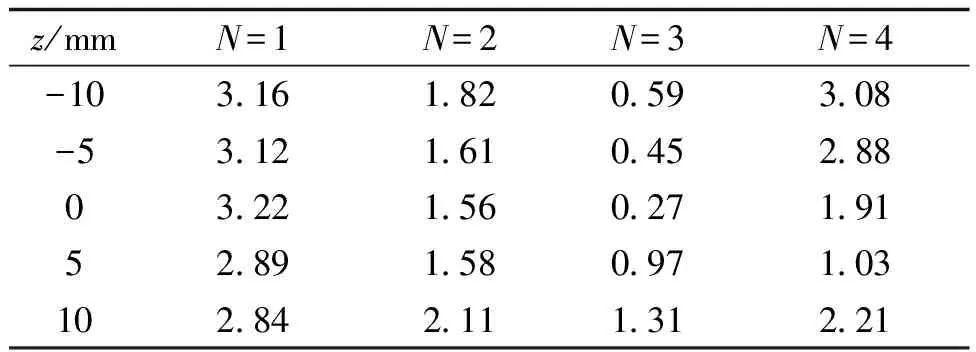
表2 不同匝数、屏蔽线圈位置情况下观察点磁感应强度

将表2中数据绘制成图8,由图8可知,当屏蔽线圈放置在与发射线圈同一水平高度处且线圈匝数为3匝时,其产生的磁屏蔽效果最佳,优于屏蔽线圈放置在发射线圈上方5 mm或下方5 mm处产生的磁屏蔽效果。

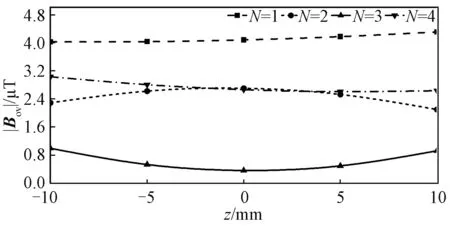
图8 不同匝数、屏蔽线圈位置情况观察点磁感应强度图Fig.8 Magnetic induction intensity diagram of observation point under different turns and shielding coil position

结合图8和式(14)分析可知,线圈匝数N对屏蔽效果的影响与Ish类似,同样存在一个阈值,当匝数N达到该阈值时,将总磁感应强度抵消为0,此时,若继续增大线圈匝数N,会产生反向增强的磁场,对磁屏蔽起消极影响。在本文设计中,3匝屏蔽线圈是一个合适的参数,与1、2匝线圈相比,屏蔽效果更加显著;与4匝线圈相比,不会产生反向磁场,影响磁屏蔽性能。故确定Ish为1.4 A,屏蔽线圈位置与发射线圈处于同一水平高度(z=0)、屏蔽线圈匝数N为3匝,达到了最佳的屏蔽效果。

3.3 抗偏移优化仿真

常态情况下,很难保证接收线圈与发射线圈完全对称放置,必须考虑到耦合线圈的抗偏移能力。因此本文在屏蔽线圈设计上除了消磁目的外,还加强了它对整个系统的抗偏移性能。在无屏蔽条件下,控制接收线圈沿x方向水平偏移15 mm、30 mm、45 mm、60 mm,仿真得到其互感值见表3。

表3 无屏蔽情况下偏移互感值Tab.3 Offset mutual inductance without shielding

由于耦合结构的中间部分磁感线较为密集,边缘位置磁感线较为稀疏,因此将屏蔽线圈设计为外层密、内层疏的圆形结构,当接收线圈发生偏移时,外层密、内层疏的屏蔽线圈会增加边缘位置磁感线,提升整个磁场的均匀度,增强耦合结构的抗偏移能力。测量得添加屏蔽线圈的条件下,接收线圈沿x方向水平偏移15 mm、30 mm、45 mm、60 mm的互感值见表4。

表4 有屏蔽情况下偏移互感值Tab.4 Offset mutual inductance with shielding

对比分析表3、表4中的数据可知,随着偏移量的增加,整体互感值均呈现减小趋势,并且偏移越大,互感值减小越多。这是因为随着接收线圈偏移距离增加,能到达该线圈的磁感线减少,所以互感值会降低。当在耦合结构中添加外层密、内层疏的屏蔽线圈后,增加了边缘位置磁感线、提升了磁场均匀度。虽然互感值会略微降低,但是与无屏蔽情况相比,同样的偏移距离下,互感降低的差值显然更小。从互感值变化较小这一方面有效说明该屏蔽设计令耦合结构的抗偏移性能提高了6.72%。

综合上述仿真结果,本文调节屏蔽电流Ish为1.4 A,其与发射线圈电流之比为1.4。对屏蔽线圈的匝数以及其所处的位置做出合理设计,令线圈匝数为3匝,且与发射线圈处于同一水平高度。选择x=220 mm的观察点位置为边界,建立一个边长为440 mm的立方体结构。以该立方体的x、y方向表面的磁感应强度为标准。对比添加屏蔽线圈前后这两个表面的磁感应强度值的变化情况,如图9所示。图9中Bmax为该区域最大磁感应强度,图9(a)为无屏蔽线圈时立体结构表面的磁感应强度分布图,图9(b)为添加屏蔽线圈后的磁感应强度分布图。根据图9中标注的磁感应强度数值,可知立体结构表面的最大磁感应强度由5.8 μT降低为2.9 μT。由此可知,在该立方体以外区域的磁感应强度值同样得到了有效降低,证明该屏蔽方法是可行的。

图9 有、无屏蔽时立体表面的磁感应强度Fig.9 Magnetic induction strength of three-dimensional surface with and without shielding

为了验证谐振屏蔽法的优越屏蔽性能,本文在Comsol软件上搭建了铁氧体屏蔽模型,与谐振屏蔽做对比。测量记录了x方向区域内的磁感应强度值(见表5),在观察点处,无屏蔽情况下的磁感应强度值为5.85 μT,从表5中数据发现在添加本文设计的屏蔽线圈后,磁感应强度值降低为0.21 μT,最大屏蔽量达到96.41%。而铁氧体屏蔽法,将磁感应强度降低为2.21 μT。其最大屏蔽量为62.22%。与铁氧体屏蔽相比,本文的谐振屏蔽提高了34.19%的屏蔽性能,突出了该设计的屏蔽优越性。

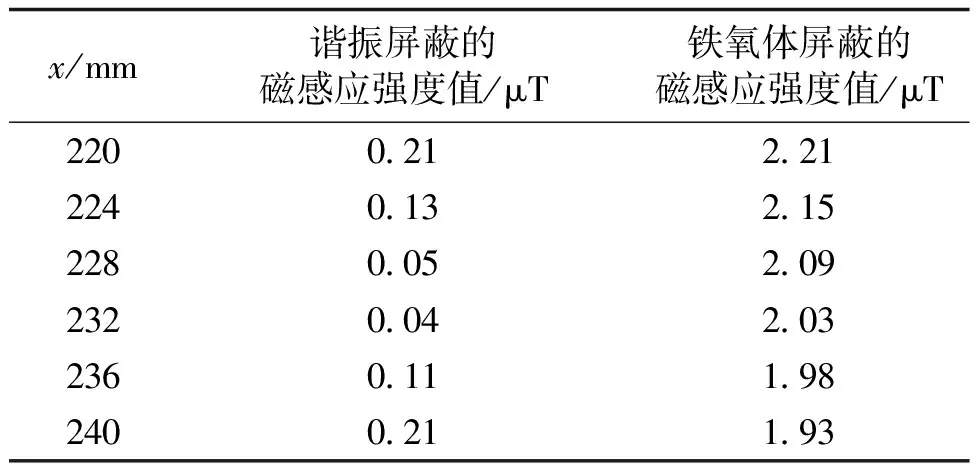
表5 两种屏蔽的磁感应强度值Tab.5 Magnetic induction value of two kinds of shielding

4 屏蔽实验验证

为验证本文所设计屏蔽方法的有效性,搭建频率为85 kHz的WPT系统结构,并采用谐振屏蔽方法实现。如图10为所构建WPT系统的实验设置。图10中直流电源向逆变器供电,逆变器将直流电转化为交流电。传输到接收线圈的交流电经过整流器转化为直流电,实现对负载的供电。耦合结构中发射线圈与接收线圈均绕制10匝,内、外径均分别为192 mm、246 mm,将其对称放置。屏蔽线圈绕制为3匝,内径为280 mm,外径为308 mm。为降低对传输效率的影响,所有线圈均采用Litz线绕制[24]。

图10 WPT系统的实验设置Fig.10 Experimental setup of WPT system

屏蔽线圈的加入势必会对原耦合结构的传输效率产生影响。文中耦合线圈及屏蔽线圈的电气参数见表6。结合式(7)可知在有屏蔽线圈条件下的耦合结构最大传输效率达到了82.2%,而无屏蔽情况下的最大传输效率计算为88.7%。系统的传输效率降低,一部分是由于收发线圈间的互感Mtr减小导致,另一部分则是因为屏蔽线圈与接收线圈之间发生耦合产生损耗。

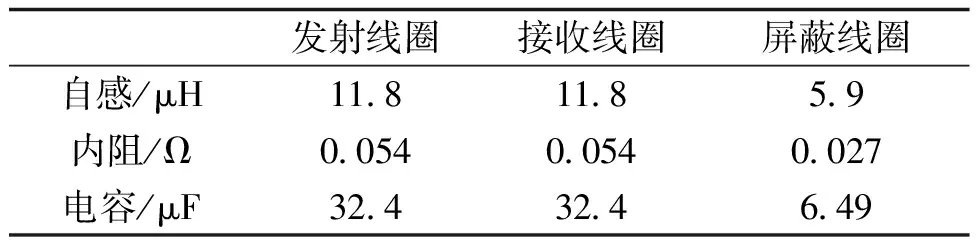
表6 耦合线圈及屏蔽线圈的电气参数Tab.6 Electrical parameters of coupling coil and shielding coil

图11为有、无屏蔽时发射线圈自感测试装置,根据LCR分析仪,在图11(a)中测得无屏蔽线圈时发射线圈自感为Lt=11.23 μH,在图11(b)中测得添加屏蔽线圈后发射线圈自感Lt降低为9.88 μH。电磁屏蔽技术可以理解为降低区域内磁感线的疏密程度,而自感值的大小同样表示磁感线的疏密,因此通过自感值的变化足以反映出磁屏蔽的效果。根据第2节的分析可知,在屏蔽线圈周围产生的屏蔽作用对耦合结构及其外部区域都会产生影响。所以通过观测发射线圈自感的降低,可以说明该屏蔽设计对耦合线圈的外部区域已经产生磁场屏蔽效果,证明了屏蔽方法的有效性。

图11 有、无屏蔽时发射线圈自感测试装置Fig.11 Self inductance test device of transmitting coil with and without shielding

5 结论

本文介绍了一种谐振屏蔽法并将其运用在圆形线圈的设计中,从而降低了无线充电过程中耦合结构周围的漏磁。首先通过分析谐振屏蔽法减弱磁场的原理,建立了等效电路模型,对传输效率做出正确推导。然后确立了屏蔽线圈的优化方案并对提高完整系统的抗偏移性能做出了合理设计。最后通过仿真软件和实验验证了谐振屏蔽法可以达到96.41%的最大屏蔽量,有效降低目标区域内的磁感应强度大小。与铁氧体屏蔽对比,提高了34.19%的屏蔽效果。通过对屏蔽线圈匝间距的合理设计,耦合结构抗偏移性能提高了6.72%,证明了该谐振屏蔽理论和设计方法的有效性。