一种面向储能系统的双向隔离型AC-DC矩阵变换器控制策略
2023-07-28慕月清赵英鹏
梅 杨, 慕月清, 赵英鹏
(北京市变频技术工程技术研究中心, 北方工业大学, 北京 100144)
1 引言
在储能系统中,双向功率变换器作为电网和储能元件的接口,是实现两者能量双向传输的一个关键环节[1,2]。高频变压器在双向功率变换器中的引入,使储能元件和电网之间的隔离被实现,系统运行更加安全可靠[3,4]。为了解决传统两级级联的双向功率变换器中大容量电容所引起的问题[5],当前已提出了单级式变换器的拓扑结构。双向隔离型AC-DC矩阵变换器是近年来面向储能系统提出的较好的拓扑结构。与之前的变换器相比,该变换器具有转换级数少、传输效率高、无大容量储能单元、功率密度高等一系列优点[6]。
目前针对储能系统中双向隔离型AC-DC矩阵变换器,常采用开环控制,其调制方法往往借鉴矩阵变换器中已提出的空间矢量调制,双线电压调制等方法[7,8]。由此双向隔离型AC-DC矩阵变换器的前级电路常采用双极性空间矢量或双线电压调制方法;后级电路常采用移相调制或互补调制方法,前后级电路间采用分段同步控制来协调配合[9-11]。近几年随着对电网电能质量和储能元件性能需求的提升,有文献在系统控制中采用了闭环控制的方法。针对变换器的并网运行模式,有文献提出采用网侧有功无功闭环控制策略,可以实现对网侧有功和无功功率的直接控制[12],但无法对直流侧的性能进行有效的控制。文献[13]采用直流电压外环和交流电流内环的双闭环结构对变换器进行控制。由于没有对直流电流直接进行控制,对直流电流的控制效果不好。文献[14]提出了一种基于空间矢量调制和前后级间移相调制的闭环控制策略,该策略同时考虑了对直流侧和网侧性能的需求。但是该控制策略中所采用的前后级间移相调制方法将会引起高频电感和高频变压器上电流应力较大的问题。
本文提出一种适用于双向隔离型AC-DC矩阵变换器的系统控制策略,将双闭环控制与变换器的后级单重移相调制方法相结合,能够同时满足电网侧的高电能质量和储能元件安全可靠充放电需求,即网侧电流正弦、电流与电压同相位、直流侧输出电压电流稳定、纹波小。本文对系统控制策略进行了相关的理论推导、仿真和实验验证。
2 电路拓扑及工作原理
图1为双向隔离型AC-DC矩阵变换器的电路拓扑,该拓扑由输入滤波器、前级3-1矩阵变换电路、电感、高频变压器、后级全桥电路、输出滤波器六个部分构成。

图1 双向隔离型 AC-DC 矩阵变换器拓扑Fig.1 Bidirectional isolated AC-DC matrix converter topology
参考双有源桥DC-DC变换器的控制思想,建立变换器中间电感两端的电压电流电路图如图2所示[15,16]。
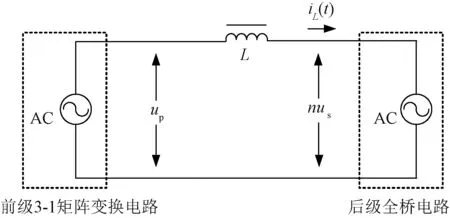
图2 中间电感两端的电压电流电路图Fig.2 Voltage and current at ends of middle inductor
由图2可知前级电路输出单相高频交流电压up,后级电路在变压器一次侧输出为单相高频交流电压nus,n为变压器的变比。两个电压源通过电感连接,电感L包括拓扑中的串联电感和变压器漏感。前后两级电压差施加在电感上,对等效电路使用基尔霍夫电压定律可得:
(1)
3 系统控制策略
本文针对双向隔离型AC-DC矩阵变换器提出了一套系统的控制策略,为同时达到对直流侧性能和网侧电能质量的较好控制,可以确立双向隔离型AC-DC矩阵变换器的控制结构如图3所示,它主要包括双闭环控制和后级单重移相调制方法两个部分。其中,双闭环控制实现变换器网侧电流和直流侧电流的有效控制,后级单重移相调制实现对变换器中开关器件开关状态的有效调制。

图3 双向隔离型AC-DC矩阵变换器的控制结构图Fig.3 Control structure diagram of bidirectional isolated AC-DC matrix converter
3.1 双闭环控制

双闭环PI控制中,为了得到网侧电流和输入侧电流之间的等量关系。需要建立网侧和输入侧之间电路的数学模型。电网、输入滤波器和矩阵变换电路的单相等效电路如图4所示。根据基尔霍夫电压和电流定律,得到网侧状态方程在三相坐标系中的表达式如式(2)所示。

图4 单相等效电路图Fig.4 Single-phase equivalent circuit diagram
(2)
式中,Lf为网侧滤波器电感;Rf为滤波器电阻;Cf为滤波器电容;ug为等效单相网侧电压;ig为等效单相网侧电流;ui为等效单相输入侧电压;ii为等效单相输入侧电流。

(3)

(4)

3.2 调制方法


图5 整流模式下3-1矩阵变换电路和后级全桥电路产生的高频交流电压、电感电流示意图Fig.5 Schematic diagram of high-frequency AC voltage and inductor current generated by 3-1 matrix converter circuit and post-stage full-bridge circuit in rectifier mode
在该调制方法下前级3-1矩阵变换电路和后级全桥电路产生的高频交流电压、电感电流示意图如图5所示。第一、第二开关状态持续时间为d1Ts/2,3-1矩阵变换电路输出电压为Umax。第三和第四开关状态持续时间为d2Ts/2,3-1矩阵变换电路输出电压为Umed。在第五段间隔中输出电压为零矢量电压中的一个。图5中Umax和Umed分别为采用双线电压法时的最大线电压和次大线电压。后级全桥电路输出为正负零电平电压,ΔT1、ΔT2为后级电路每一段的移相调制作用时间,ΔT1=δd1Ts/4,ΔT2=δd2Ts/4,其中Ts=2π/ωs,φ为移相角,整流模式下0≤φ≤π/2,δ=2φ/π,δ为移相比,取值范围为 0≤δ≤1。由图5及式(1)可得图5中九段电感电流的表达式如式(5)所示,其中iL0为电感电流初值。
(5)
根据文献[1]关于对占空比的相关计算可得,在偶数扇区中Umax、Umed和零电压分别作用对应的占空比d1、d2、d0如式(6)所示:
(6)

同理可得在奇数扇区Umax、Umed和零电压分别作用对应的占空比d1、d2、d0如式(7)所示:
(7)
(8)
(9)
式中,Ui为网侧电压幅值;Uo为输出电压;φi为功率因数角;ωs为控制角频率。
从式(8)、式(9)中可得在后级单重移相调制方法中移相角分别与输入输出电流的关系式。在控制过程中通过对调制方法中一个控制变量即移相角的适当调整,可较简单实现对变换器性能较好的控制效果,该调制方法可与整体控制结构形成合适的配合,最后达到对变换器一种较为简单实现的控制。
4 仿真及分析
对以上推导的理论结果有效性进行验证,使用Matlab/Simulink搭建本文提出的变换器控制系统整体模型,进行控制效果的仿真验证,仿真中设置的相关参数见表1。

表1 变换器的仿真参数Tab.1 Simulation parameters of converter
4.1 整流模式
整流模式下仿真中给定直流侧输出电流参考值为2.54 A。直流侧与网侧电流双闭环控制稳态仿真结果如图6所示,从图6(c)中可以看出输出电流可较好地达到给定参考量,波形稳定、波动小。分析图6(b)可得直流侧输出电压纹波约为 0.12%。变换器的网侧功率因数指网侧电压与网侧电流之间相位差的余弦值,图6(a)中网侧电压、电流相位差为8°,由此可得到网侧功率因数为0.99(cos8°=0.99),a相电流总谐波畸变(Total Harmonic Distortion,THD)为2.12%。双闭环控制策略可以满足网侧电能质量和直流侧负载的基本需求,对变换器的输入输出性能实现良好的静态控制效果。
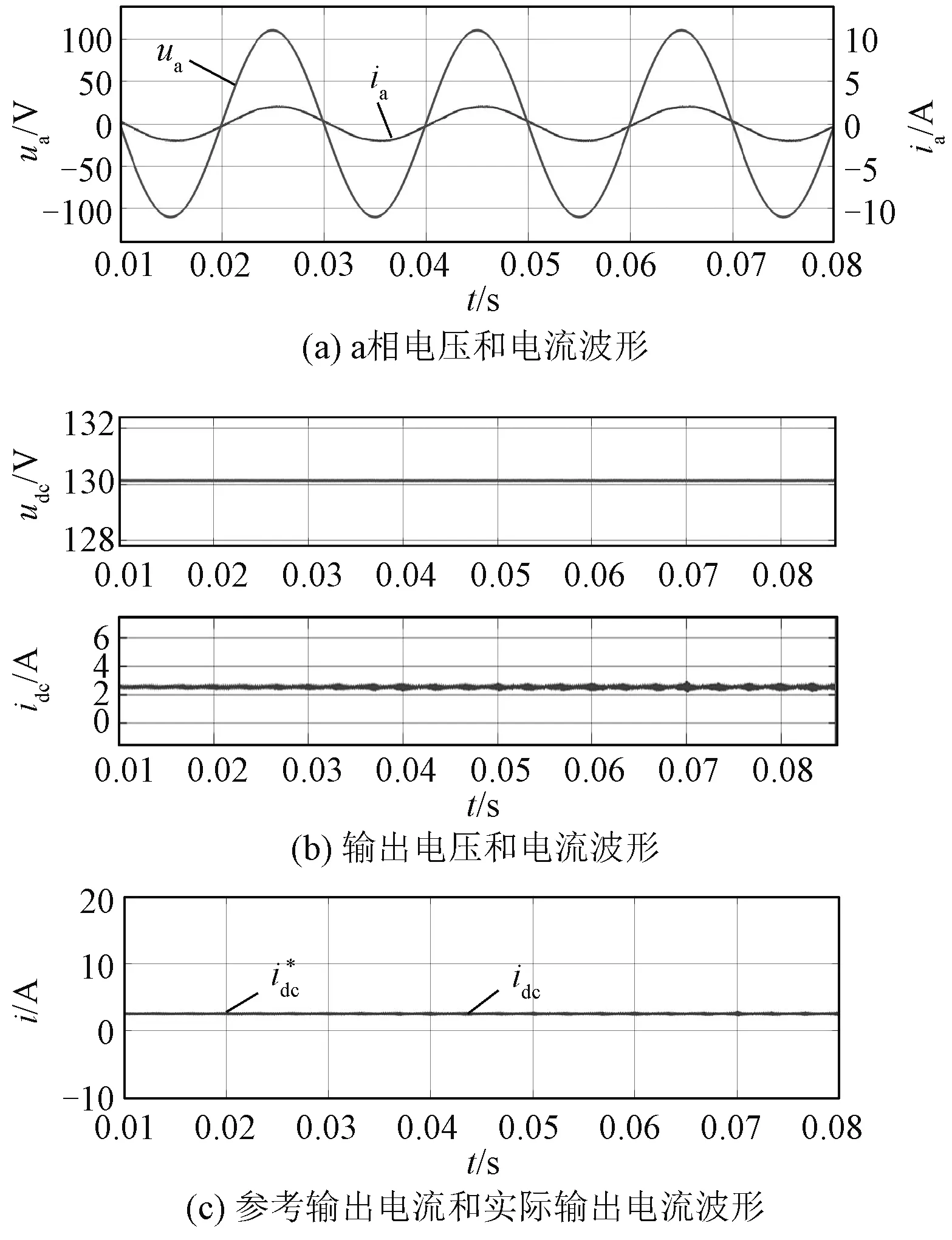
图6 整流模式下控制策略的稳态仿真结果Fig.6 Steady-state simulation results of control strategy in rectification mode
为验证动态性能,0.03 s时使输出电流由2.54 A突变为2 A。从图7中可看出在t=0.034 s时系统快速恢复稳定,无超调,且输出电流io能够较好地随着参考值相应改变,网侧电压不变,三相电流相应变化,网侧a相电流THD为3.76%。表明控制策略使变换器具有较好的动态特性。

图7 整流模式下控制策略的动态仿真结果Fig.7 Dynamic simulation results of control strategy in rectification mode
4.2 逆变模式
逆变模式下仿真中给定直流侧输出电流参考值为-1 A。直流侧与网侧电流控制稳态仿真结果如图8所示,从图8(c)中可以看出直流电流idc较好地跟随给定参考电流值,波形稳定。从图8(a)分析得到网侧a相电流THD为1.58%,电流与电压相位差约为180°,功率因数为-0.989。图8(b)中可得输出电压纹波约为0.08%,输出电压和输出电流波动小。控制策略同样使变换器具有良好的静态特性,整体电能质量高,可以实现功率的双向传输要求。

图8 逆变模式下控制策略的稳态仿真结果Fig.8 Steady-state simulation results of control strategy in inverter mode
为了验证动态性能,当0.1 s时使输出电流由-1 A突变为-1.5 A。从仿真结果图9中可以看出在突变瞬间电流有小幅波动,t=0.12 s时系统快速恢复稳定,无超调,且输出电流idc能够随着给定参考量的不同而相应改变,网侧三相电压不变,电流相应变化,网侧a相电流THD为2.1%。表明控制策略使系统具有良好的动态性能。
5 实验验证
为验证所提出控制策略的可行性与有效性,在一台双向隔离型AC-DC矩阵变换器的样机上进行实验,实验平台如图10所示,实验关键参数见表2。

表2 实验关键参数Tab.2 Experimental parameters

图10 实验平台Fig.10 Photo of experimental platform
5.1 整流模式
实验中给定直流侧输出电流参考值为1.2 A。直流侧与网侧电流双闭环控制实验结果如图11所示,网侧电流与电压相位差基本为0°,网侧a相电流THD为2.54%,输出电压和输出电流波动小,波形平稳。实验结果表明采用提出的系统控制策略,可以同时达到对网侧和直流侧性能的较好控制。为了验证系统动态性能,使得直流侧输出电流从0.3 A突变为1.2 A,实验结果如图12所示。从图12(a)中可以看出电流突变时,经过1.04 s的时间,电流能够跟踪上参考值,系统快速达到新的稳定状态。网侧输入a相电流跟随直流侧电流变化而变化。直流侧电流控制策略使变换器具有良好的动态特性。

图11 整流模式下控制策略的稳态实验波形Fig.11 Steady-state experimental waveform of control strategy in rectification mode
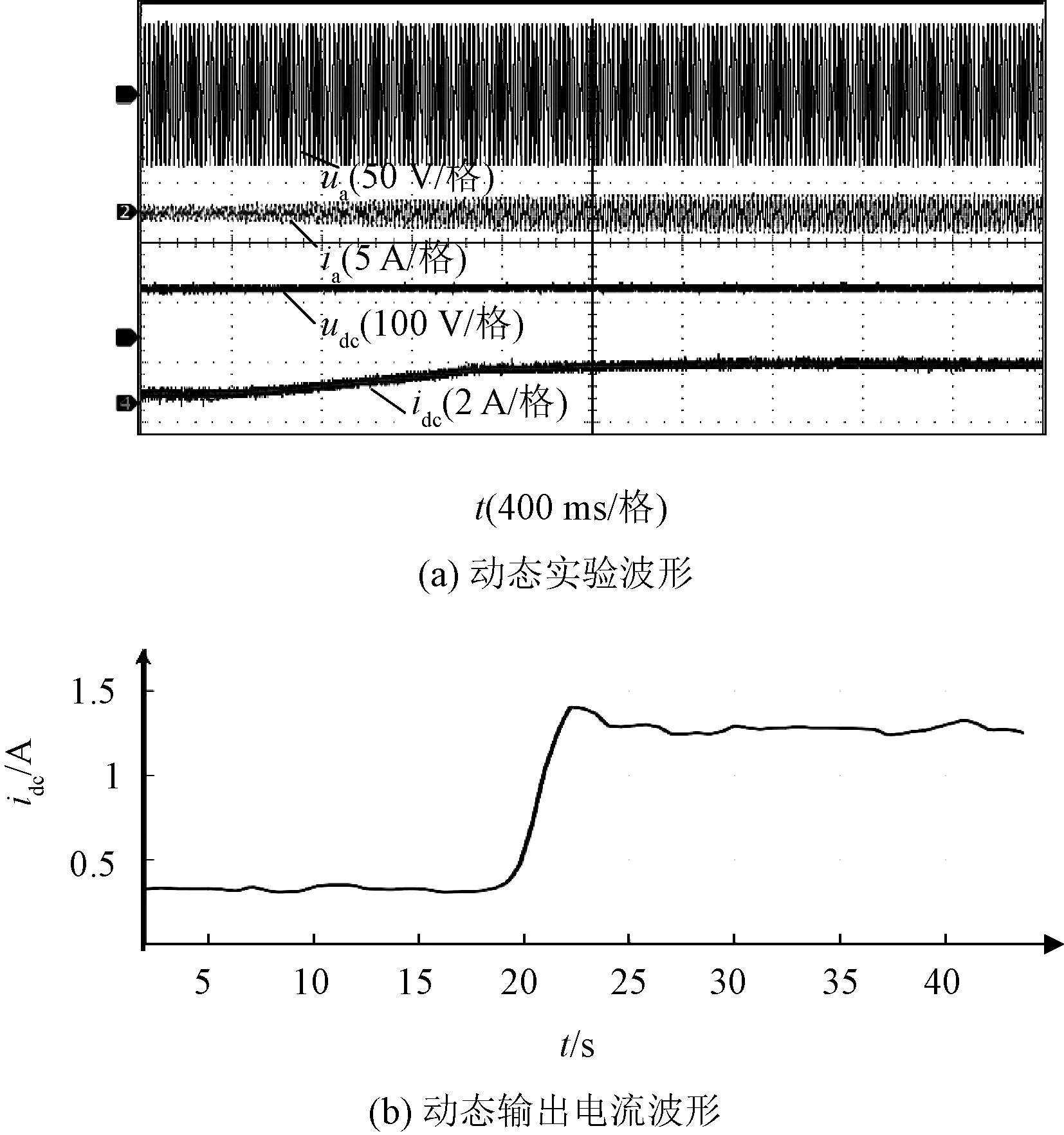
图12 整流模式下控制策略的动态实验波形Fig.12 Dynamic experimental waveform of control strategy in rectification mode
5.2 逆变模式
同样实验条件下,逆变模式中给定直流侧输出电流参考值为-1.2 A。双闭环控制稳态实验结果如图13所示,分析可得网侧a相电流THD大小为4.57%,网侧电流与电压相位差约为180°,直流侧输出电压纹波较小,输出电流较好地达到给定值,波形稳定。实验表明提出的控制策略使变换器具有良好的静态特性,整体电能质量高,实现功率双向传输。为了验证系统动态性能,使得输出电流从-0.3 A突变为-1.2 A,实验结果如图14所示。从图14(a)中可以看出,发生电流突变时,经过1.52 s,电流能够跟踪上参考值,系统快速达到新的稳定状态,输入a相电流跟随直流侧电流变化而变化,逆变模式下系统控制策略同样使变换器具有较好的动态特性。
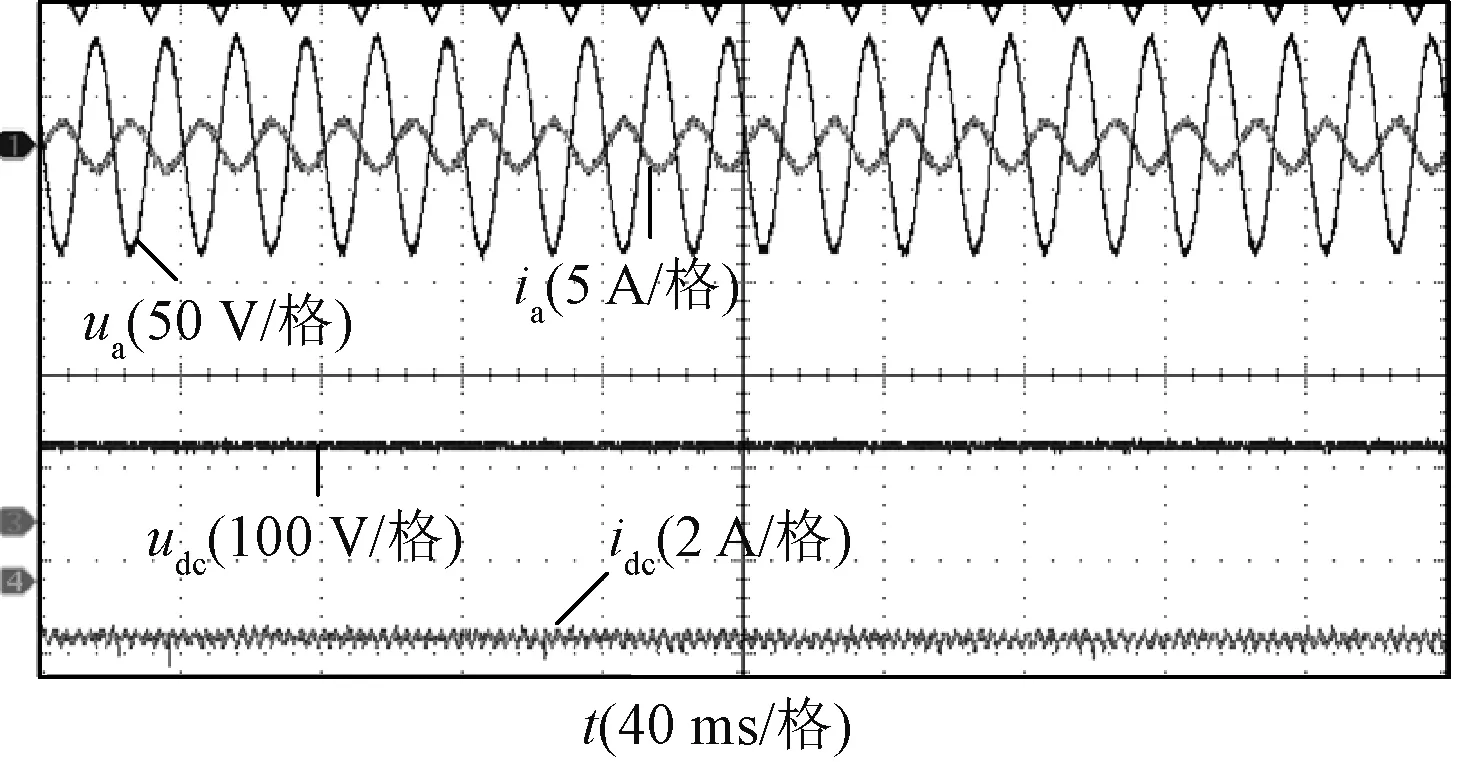
图13 逆变模式下控制策略的稳态实验波形Fig.13 Steady-state experimental waveform of control strategy in inverter mode

图14 逆变模式下控制策略的动态实验波形Fig.14 Dynamic experimental waveform of control strategy in inverter mode
5.3 整流与逆变模式的切换
图15为双闭环控制策略下整流模式向逆变模式切换的实验波形。可以看出不同工作模式之间切换速度快、过渡时间较短、波形切换平滑。

图15 整流模式与逆变模式间切换实验结果Fig.15 Experimental results of switching between rectifier mode and inverter
6 结论
本文针对储能系统用双向隔离型AC-DC矩阵变换器,提出一种系统控制策略,对提出的策略进行了理论分析与相应的仿真和实验验证,结果证明所提出的控制策略具有以下优势:
(1)电网侧功率因数可达0.99,网侧电流正弦,直流侧电流电压波形平稳,纹波在0.15%以内,具有良好的网侧电能质量和直流侧静态性能。
(2)直流侧电流发生突变,充电情况下动态跟踪时间在1.1 s以内,放电时间在1.6 s以内,电流跟踪速度快、超调接近零、直流侧动态特性好。
