基于TensorFlow神经网络的MCR-WPT系统负载与互感识别方法
2021-09-25苏玉刚刘家鸣侯信宇
苏玉刚,阳 剑,戴 欣,刘家鸣,侯信宇
(1.重庆大学自动化学院,重庆市 400030;2.国家无线电能传输技术国际联合研究中心,重庆市 400030)
0 引言
无线电能传输(wireless power transfer,WPT)技术作为一种安全、环保、便捷、易维护的新型供电方式,受到了国内外众多学者的关注和研究[1-3]。其中,磁耦合谐振式无线电能传输(magnetic coupling resonant wireless power transfer,MCR-WPT)技术是目前最受关注的技术[4-6],在电动汽车[7-8]、航空航天[9]、水下设备供电[10]等领域逐步得到推广应用。
在MCR-WPT系统的实际应用中,对于电动汽车等移动设备无线供电系统,其负载与互感不可避免地会发生变化,这种变化不仅会使系统的工作频率发生漂移[11-12],而且会降低系统的传输功率和传输效率[13]。如果没有负载与互感识别环节,针对负载与互感发生变化的情况,为了保持系统较好的传输性能,目前主要有以下3种控制方法:①在发射端进行控制;②在接收端进行控制;③在发射端和接收端同时进行控制。上述3种方法通过在接收端增加额外的通信设备[14]、Buck变换器[15]、可控开关[16]等辅助手段对系统进行调节和控制,其对系统性能的提升具有一定的效果,但不能从根本上解决因负载与互感宽范围变化导致的系统工作频率漂移、工作特性改变等问题。因此,在MCR-WPT系统中当负载和互感发生变化时,系统需要实时获取负载与互感参数信息,进而采取更有效的手段对系统进行控制以确保系统稳定、高效运行,而负载与互感参数识别正是其中的关键问题[17-19]。
目前已有学者围绕MCR-WPT系统的负载与互感识别技术进行了相应的研究,文献[18]通过建立SS型MCR-WPT系统稳态电路模型,利用遗传算法寻求负载最优解进而得到互感值。文献[19]以接收端为并联补偿形式的MCR-WPT系统为研究对象,通过检测系统工作频率、逆变器的输出电压和电流,根据系统稳态电路模型计算得到负载与互感值。文献[20]通过切换SS型MCR-WPT系统频率,使其工作在非工作频率点上完成对负载与互感的识别。文献[21]通过在SS型MCR-WPT系统发射端增加一套辅助逆变器和匹配的耦合机构,使系统工作在不同模式下完成对负载与互感的识别。文献[22]通过可变开关电容和蓝牙通信模块实现发射端和接收端电路谐振状态的改变,进而识别出LCC/S型MCR-WPT系统的互感值。
现有研究中的MCR-WPT系统负载与互感识别方法主要存在以下问题:①大多数识别方法研究主要以SS型MCR-WPT系统偏多,其中部分识别方法只能识别负载或互感中的单一参数;②有的识别方法对系统建模精确性要求较高,且需要运行迭代算法,识别时间相对较长;③有的识别方法需要在接收端进行电路参数检测,增加了系统体积和成本;④还有的方法需要改变系统的工作频率来进行识别,影响了系统的传输性能。
针对上述问题,本文提出了基于TensorFlow神经网络的双LCC型MCR-WPT系统负载与互感识别方法。通过对双LCC型MCR-WPT系统进行建模分析,得到了识别模型的输入参数,将MCRWPT系统的负载与互感识别问题等效为非线性方程的求解问题,进而转化为深度学习非线性拟合问题。本文首先建立TensorFlow神经网络负载与互感识别模型,通过设置不同的偏移距离d和传输距离h得到互感M的训练数据,再将训练数据输入模型进行离线训练,训练完成后将识别模型导入控制器进行在线识别。在线识别时,只需要检测输入电流值和传输距离,调用识别模型计算得到负载值与互感值。仿真与实验结果验证了本文提出方法的正确性和有效性。
1 双LCC型MCR-WPT系 统
双LCC型MCR-WPT系统具有发射端和接收端结构对称、补偿拓扑网络易配谐、输出电流与负载无关等特性,抗偏移性好,被广泛应用在电动汽车等无线充电系统中[6-7]。
图1所示为双LCC型MCR-WPT系统等效电路。图中:U˙in为直流电源经高频逆变电路后输出的高频交流 电压源,频率为ω;I˙in为输入电流;L1为发射线圈自感;R1为发射线圈内阻;L2为接收线圈自感;R2为接收线圈内阻;M为发射线圈与接收线圈之间的互感值;发射端补偿电感Lf1、发射端补偿电容Cf1与发射端谐振电容C1构成发射端补偿网络;接收端补偿电感Lf2、接收端补偿电容Cf2与接收端谐振电容C2构成接收端补偿网络;Req为整流环节和负载等效电阻。
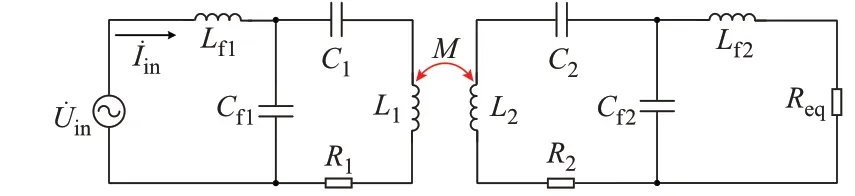
图1 双LCC型MCR-WPT系统等效电路Fig.1 Equivalent circuit of double-side LCC type MCR-WPT system
2 系统建模及识别方法
本文针对目前负载与互感识别方法速度慢、精度低等问题,提出了基于TensorFlow神经网络的负载与互感识别方法,下文以双LCC型MCR-WPT系统为例进行说明。为了确定TensorFlow神经网络的负载与互感识别模型的输入参数,需要对双LCC型MCR-WPT系统进行建模分析。
2.1 系统建模
双LCC型MCR-WPT系统接收端等效电路模型如附录A图A1所示。根据文献[19,23]中研究可知,影响系统性能的最主要因素是负载与互感的变化,而接收端补偿网络、整流二极管等环节的电路参数会随着温度的变化而变化,但其变化很小,对系统的性能影响较小。因此,为了减小负载与互感识别的复杂度,本文将这部分参数视为常数。
在附录A图A1中,接收线圈拾取到的高频交流电压记为U˙2,接收端输入阻抗记为Z2,其表达式为:
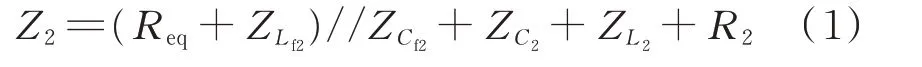
式中:ZCf2=1/(jωCf2)、ZC2=1/(jωC2)、ZLf2=jωLf2、ZL2=jωL2。
在系统完全谐振时,代入式(1)可以得出接收端电路整体阻抗为:
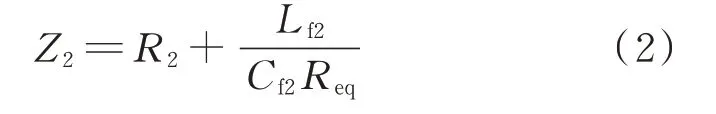
由于对系统进行负载与互感识别主要通过从发射端检测相关参数来进行分析,因此,为进一步分析负载与互感变化对系统的影响,需要将双LCC型MCR-WPT系统发射端电路简化为附录A图A2所示的等效电路。在系统完全谐振时,接收端电路在发射端电路的反射阻抗Z21可以表示为:
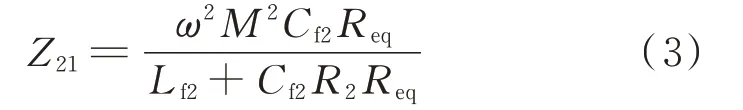
从式(3)可以看出,负载与互感变化对系统的影响具体表现为反映到系统发射端的反射阻抗的变化。进一步,输入阻抗Zin与输入电流有效值Iin有如下关系成立:

其中发射端输入阻抗Zin为:
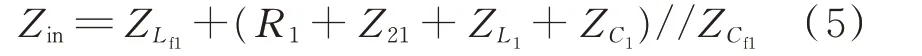
将式(3)代入式(5)中并取ZLf1=jωLf1、ZL1=jωL1、ZC1=1/(jωC1)、ZCf1=1/(jωCf1),在系统完全谐振时可得:
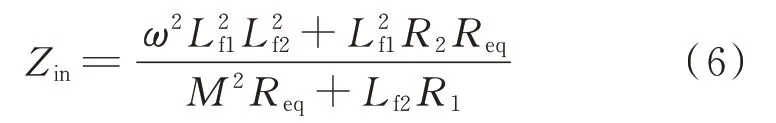
将式(6)代入式(4)中,可得负载等效电阻Req和互感M与输入电流Iin的关系式为:
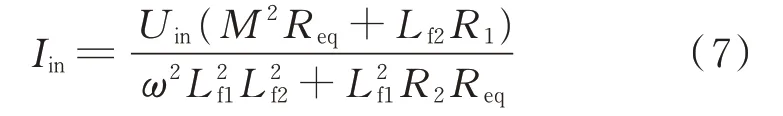
由式(7)可以看出,系统输入电流有效值Iin受到负载等效电阻Req和互感值M的影响,故可以通过检测输入电流值来进行负载与互感的识别。然而,仅通过输入电流有效值Iin还不能确定负载与互感的值,因此还需要检测其他的参数。
根据文献[24]可知,在相同尺寸的条件下圆形线圈的互感值最大,系统抗偏移性能最好,故本文选择圆形线圈作为系统的耦合机构。对于二维平面移动设备的无线供电系统,发射线圈和接收线圈大多数是平行的,对于这类无线供电系统其偏移角度变化较小。根据文献[25]所做研究工作可知,发射线圈和接收线圈偏移角度在0°~20°的变化范围内,电动汽车无线充电系统的输出功率和传输效率主要受到传输距离和偏移距离的影响,受到角度偏移影响较小,因此,本文只考虑两圆形线圈平行情况下传输距离和偏移距离变化影响下的互感识别。根据上述分析,在发射线圈和接收线圈所在平面平行的前提下,线圈匝数和几何尺寸确定后的互感值M只与传输距离h和偏移距离d有关,如附录A图A3所示。
互感值M和d、h的关系可以用隐函数描述为:

从式(8)可以看出,只要确定了传输距离h和偏移距离d就可以确定互感的值,其中传输距离h可以采用性价比较高的红外测距传感器模块来进行检测,但偏移距离的检测比较困难,需要使用摄像头、毫米波雷达等传感器进行检测,成本较高,且在一些WPT技术应用场合中使用受限。根据式(7)可知,互感值M的变化会反映到输入电流有效值Iin的变化上,而输入电流值因为系统保护或控制本身需要检测,故只需再额外检测传输距离即能识别互感值。在互感值M确定之后,可以通过式(7)直接计算得到负载等效电阻Req的值,但式(7)是在忽略了补偿电感内阻等电路参数的前提下推导得到的,计算得到的结果识别误差相对较大,因此,文中考虑利用深度学习技术,通过检测系统输入电流值和传输距离值对互感值M和负载Req进行同时识别,最终得到:
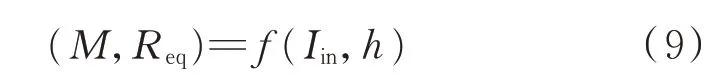
从上述分析可知,要进行负载与互感识别可以通过检测输入电流有效值Iin和传输距离h来实现。负载与互感的识别问题进一步转化为了求解非线性方程式(9)中函数f的问题。本文将基于TensorFlow深度学习框架,建立神经网络模型,通过非线性拟合的方式进行函数f的近似求解。
2.2 TensorFlow神经网络的负载与互感识别模型及方法
近年来,深度学习技术在学术界和工业界发展迅速,它在很多传统的识别任务如图像识别、语音识别、文本识别上取得了显著成效,显示了其处理复杂识别任务的能力,吸引了众多专家学者研究其理论与 应 用[26]。在MCR-WPT系 统 研 究 领 域 中,文 献[2]基于机器学习技术在WPT系统传输距离变化时,使用前馈神经网络算法实现了可调谐振网络和多个发射线圈的自动匹配,实现了最大的系统能量传输效率。
TensorFlow是由谷歌(Google)公司开发的一款开源深度学习框架,被广泛应用于机器学习领域中。TensorFlow支持跨平台操作,可以在CPU、GPU以及Android等移动平台运行,具有良好的扩展性和灵活性,同时支持多种编程语言,如C、C++、Python、Java等编程语言[27],是目前应用最为广泛的深度学习框架之一。
基于TensorFlow神经网络框架,本文提出了双LCC型MCR-WPT系统的负载与互感识别方法,如图2(a)所示。负载与互感识别时,将电流值输入系统,传输距离值输入控制器,其中输入电流值Iin的检测采用霍尔传感器实现,传输距离h的检测采用性价比较高的红外测距传感器模块来实现,控制器调用TensorFlow神经网络负载与互感识别模型,根据输入参数进行实时运算完成负载与互感识别。TensorFlow神经网络负载与互感识别模型通过离线建立并训练完成后,装载到微控制器中进行在线识别。TensorFlow神经网络负载与互感识别模型建立步骤如图2(b)所示。

图2 基于TensorFlow神经网络的负载与互感识别方法Fig.2 Load and mutual inductance identification method based on TensorFlow neural network
根据式(7)至式(9),确定将检测系统的输入电流Iin和h作为负载与互感识别模型的输入参数,基于TensorFlow框架建立了一个5层的负载与互感识别全连接神经网络模型,如图3所示。在负载与互感识别神经网络模型中,隐藏层的非线性激活函数使用TensorFlow框架中的Sigmoid激活函数。

图3 负载与互感识别神经网络模型Fig.3 Neural network model of load and mutual inductance identification
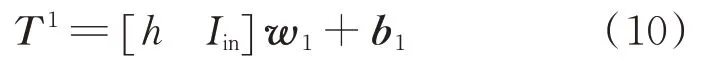
式中:T1为隐藏层1的中间变量矩阵;[h Iin]为由MCR-WPT系统的线圈间传输距离和输入电流值构成的输入矩阵;w1和b1分别为输入层与隐藏层1之间的权重矩阵和偏置矩阵,即
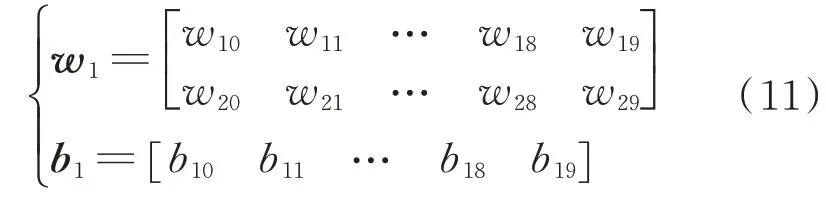
将中间变量矩阵T1中的每个元素代入Simgoid激活函数非线性化后可得隐藏层1的输出矩阵N1:
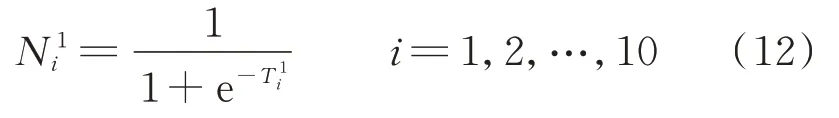
式中:T1i为隐藏层1的中间变量矩阵T1的第1行第i个元素;N1i为隐藏层1的输出矩阵N1的第1行第i个元素。
依此类推,可得T2、N2、T3、N3、T4、N4的表达式,进而得到互感值与负载为:

2.3 TensorFlow神经网络的负载与互感识别模型训练方法
模型建立后,为了确定权重矩阵和偏置矩阵w1、b1、w2、b2、w3、b3、w4、b4的值,需要使用训练数据集对模型进行离线训练,使得TensorFlow神经网络负载与互感识别的精度达到期望值。为达到上述目的,可以通过设置不同的偏移距离d和传输距离h得到互感值M的训练数据集,通过将训练数据输入模型进行离线训练,训练完成后将识别模型导入控制器进行在线识别。
本文采用仿真软件建立系统仿真模型的方式获取上述模型训练所需数据,在COMSOL多物理场仿真软件中建立了耦合机构仿真模型如附录A图A4所示。根据横向项目实际需求,耦合机构中没有加入磁芯,仿真参数如附录A表A1所示。
通过在COMSOL多物理场仿真软件中进行耦合机构仿真,得到发射线圈和接收线圈自感均为534μH。在仿真中,通过设置不同的偏移距离d和传输距离h得到互感值M,进行参数化扫描仿真后获取了483组h、d和M的数据集,如图4所示。从图中可以看出,互感值关于水平位置偏移对称变化,且当偏移距离不变时,互感值随着传输距离的增大而减小。
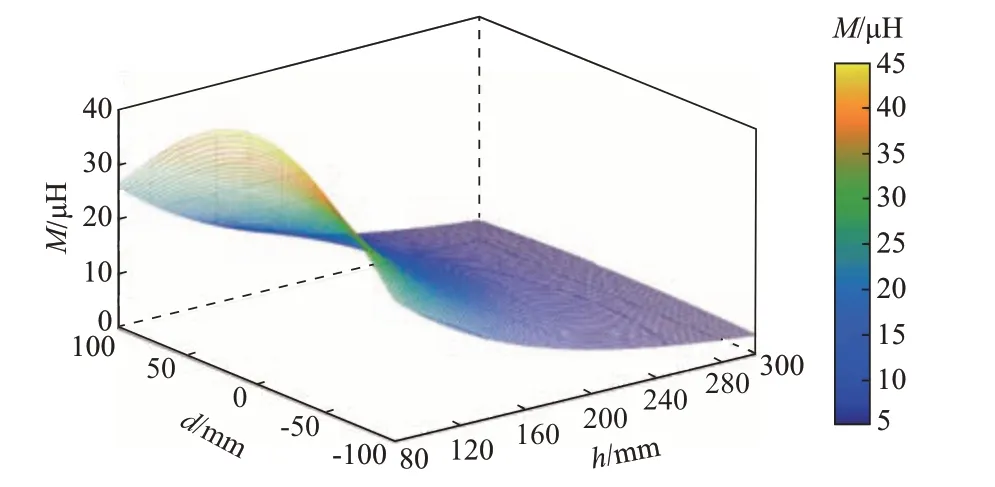
图4 d、h与M间的三维曲面图Fig.4 Three-dimensional surface diagram between d,h and M
获得传输距离h和互感值M的耦合机构仿真数据集后,在Simulink中建立了双LCC型MCR-WPT仿真模型,单次仿真时间设置为0.02 s,此时系统已经稳态运行。模型中的传输距离h和互感值M的设置使用COMSOL软件仿真的h和M数据输入,模型中的其余参数设置如下:系统频率f=80 kHz、L1=L2=534μH、C1=C2=8.48 nF、Lf1=Lf2=67μH、Cf1=Cf2=59 nF、Req=10~100Ω。
通过编写M文件进行自动仿真,每改变一次传输距离h和负载等效电阻Req,得到系统输入电流值Iin和互感值M,从而获取了2 400组仿真模型数据。
为了提高TensorFlow神经网络负载与互感识别模型的泛化能力,随机选取其中2 160组数据作为训练集、240组数据作为测试集,测试集不参与模型训练,仅用于测试模型识别效果,以检验模型的泛化能力。通过将训练集数据输入模型,根据训练误差值使用TensorFlow优化器AdamOptimizer优化模型中的参数,直至识别误差值降至设定值。如附录A图A5所示,经过10 000次训练后,模型识别误差值已经降至很小,此时训练集负载Req识别精度为98.2%,互感值M识别精度为98.3%,在测试数据集中负载Req识别精度为98.0%,互感值M识别精度达到98.5%,至此,TensorFlow神经网络负载与互感识别模型完成训练。
模型训练完成后,导出权重矩阵和偏置矩阵w1、b1、w2、b2、w3、b3、w4、b4的值,在线识别负载与互感时,通过检测系统输入电流值Iin和传输距离h,将上述导出的权重矩阵和偏置矩阵在微型控制器中进行如式(14)所示的运算,得到负载与互感值。
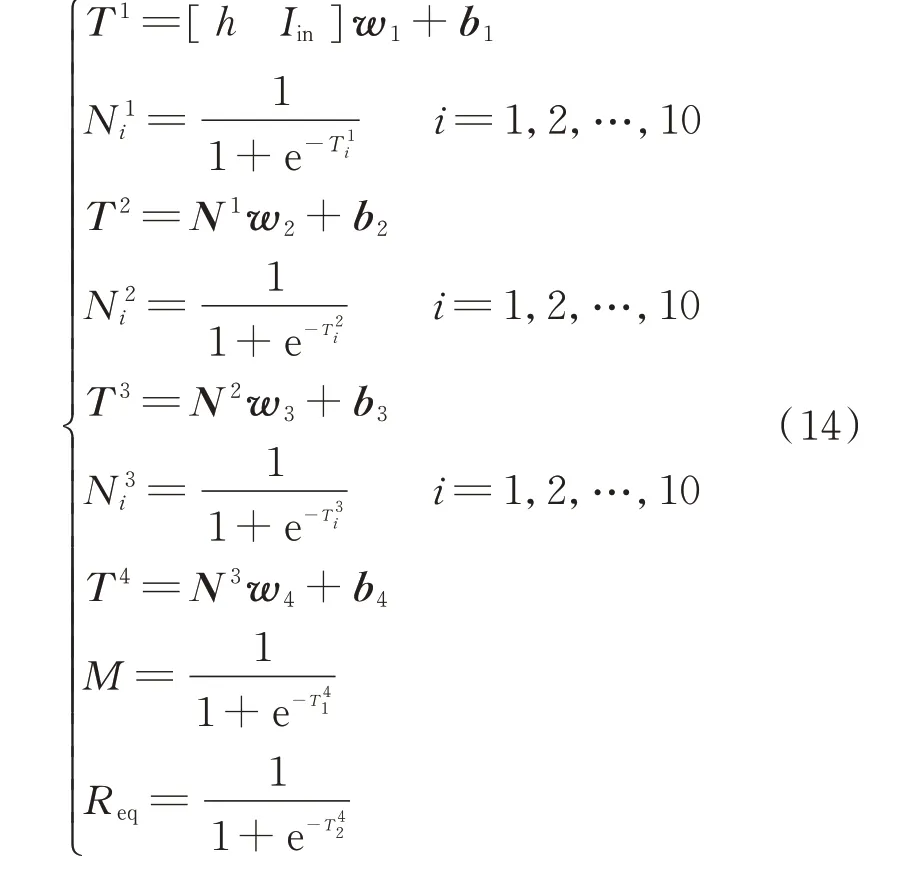
3 仿真分析
为验证所提识别方法的可行性和识别效果,本文 基 于 双LCC型MCR-WPT系 统 和 上 述TensorFlow神经网络负载与互感识别模型建立了如附录A图A6所示的Simulink仿真验证模型。该模型主要由以下几个部分组成:①双LCC型MCRWPT系统主电路;②逆变电路信号发生模块;③发射端LCC拓扑网络输入电流值Iin和传输距离h采集单元,仿真中电流值Iin通过检测模块实时检测,传输距离h通过编程自动输入改变;④识别模型算法单元。双LCC型MCR-WPT系统仿真参数与2.3节系统仿真模型一致。
在仿真验证模型中,通过编写M语言将基于TensorFlow神经网络的负载与互感识别模型算法(式(14))封装在附录A图A6中的识别模型算法单元中,识别算法一次运算耗时约为25μs,负载与互感仿真参数设置如表1所示,其中偏移距离为0 mm时,发射线圈与接收线圈中心对齐。互感设定值M通过传输距离h和偏移距离d变化而设定,传输距离h设定值在80~300 mm变化,偏移距离d设定值在0~100 mm变化,进而使得互感值M设定值在45.40~4.41μH变化。负载Req设定值则直接设定为10~100Ω变化。

表1 负载与互感仿真参数Table 1 Simulation parameters of load and mutual inductance
参数设置完成后,运行仿真模型,通过调用TensorFlow神经网络负载与互感识别模型可以在线同时识别负载与互感值,识别结果如图5所示。
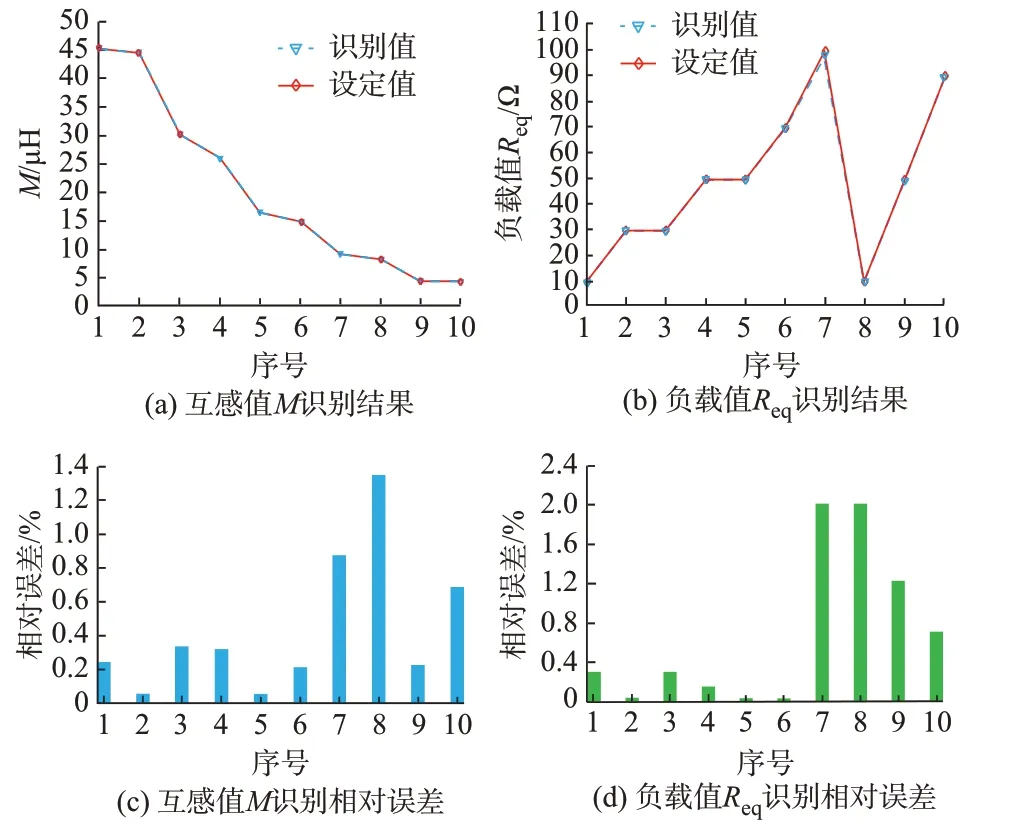
图5 负载与互感识别仿真结果Fig.5 Simulation results of load and mutual inductance identification
分析负载与互感识别仿真结果可以看出,互感值在45.40~4.41μH变化时,互感值识别最大相对误差为1.34%;负载值在10~100Ω变化时,负载值识别相对最大误差为2.0%,负载与互感识别值与设定值非常接近,识别精度较高、适应范围较大。
4 实验验证
为进一步验证所提识别方法,搭建了双LCC型MCR-WPT系统实验装置如附录A图A7所示,系统实验参数与仿真参数一致。系统控制器采用了性价比较高的STM32F103VCT6微型处理器,处理器最高工作频率为72 MHz,将离线训练完成的负载与互感识别模型编程实现后下载到控制器中。
实验中,通过切换负载以及调节发射线圈和接收线圈之间的相对位置来实现负载及互感的变化,通过霍尔传感器检测系统输入电流,经过处理后得到有效值Iin,通过GP2Y0A21YK0F红外测距传感器检测传输距离h,在微控制器中调用TensorFlow神经网络负载与互感识别模型。从检测电流值和传输距离值开始到通过TensorFlow神经网络的负载与互感识别模型计算出负载和互感值结束的时间为单次负载和互感识别时间,通过处理器的定时器模块(计时基数为1μs)进行测量得到单次识别时间约为0.76 ms。从单次识别时间可以看出,本文的负载与互感识别时间并不是很短,其主要原因是本文实验中选用的微控制器处理速度还不是很快,如果采用高速处理器,则负载与互感识别时间还能进一步缩短。16次负载与互感识别实验结果如表2所示。
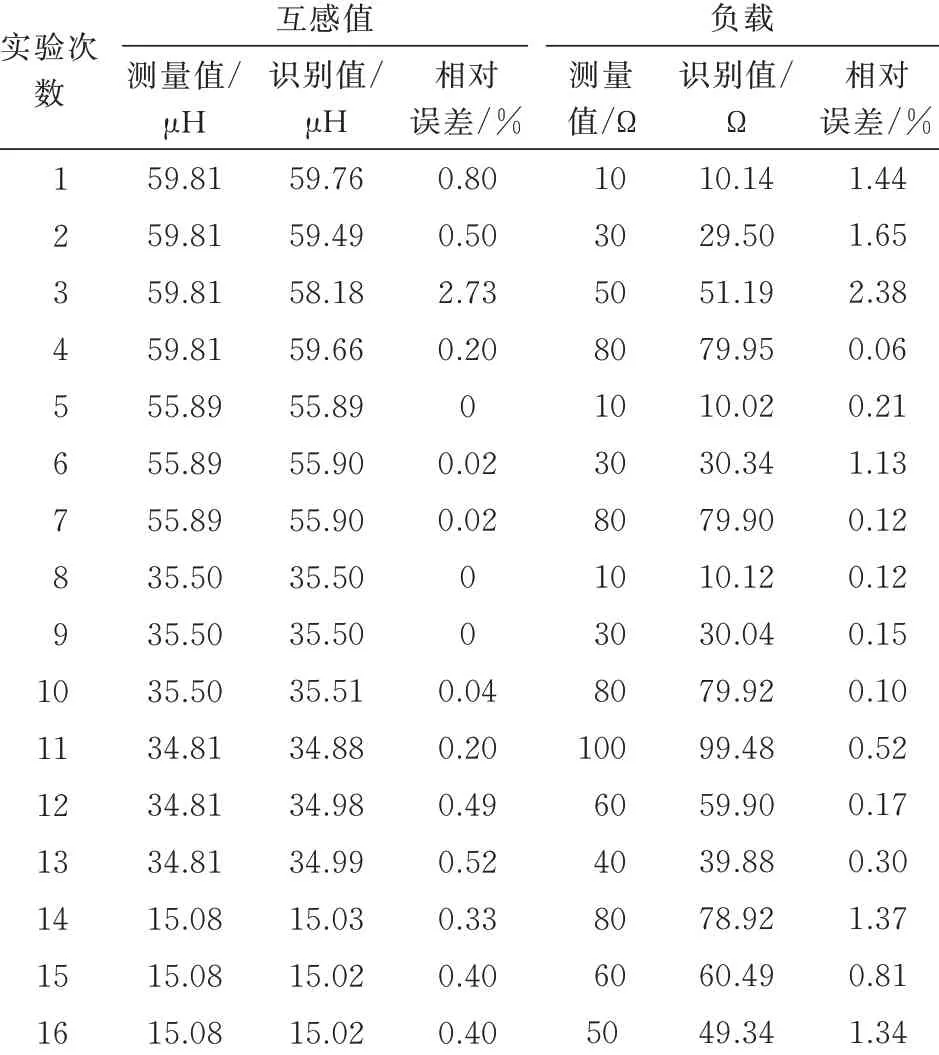
表2 LCC型MCR-WPT系统负载与互感识别实验结果Table 2 Experimental results of load and mutual inductance identification of LCC type MCR-WPT system
在1~4次实验中,传输距离设置为80 mm,偏移距离设置为0 mm,互感采用LCR测试仪IM3536测量,测量值为59.81μH,负载使用IT8813电子负载分别设定为10、30、50、80Ω。在此条件下调用负载与互感识别模型进行识别,互感识别最大相对误差为2.73%,负载识别最大相对误差为2.38%。
在5~7次实验中,保持传输距离不变,改变线圈相对位置使得偏移距离为20 mm,互感测量值为55.89μH,负载分别设定为10、30、80Ω。通过调用负载与互感识别模型得到互感识别最大误差为0.02%,负载识别最大误差为1.13%。
进一步调整线圈相对位置,增加传输距离至100、110、150 mm并设定相应的负载值完成了8~16次负载与互感识别实验。互感识别最大相对误差为0.52%,负载识别相对最大误差为1.37%。
从上述实验结果可以看出,本文设置互感值在15.08~59.81μH变化时,互感识别最大相对误差为2.73%;负载在10~100Ω变化时,负载识别最大相对误差为2.38%,与仿真结果基本一致。相较于文献[22]中的单一参数识别,互感识别相对误差为5.0%,本文实现了负载与互感在线同时识别,且识别精度有较大提升;在文献[18-21]负载与互感双参数识别方法研究中,相对误差为7.4%,而本文负载与互感识别最大相对误差降低到了2.73%,且识别算法中无迭代运算,识别速度快,能适应更大的负载与互感变化范围,更有利于系统的实时控制和提高控制性能。
5 结语
本文针对MCR-WPT系统的负载与互感识别速度慢、精度低等问题,提出了一种基于TensorFlow神经网络的双LCC型MCR-WPT系统负载与互感识别方法。该方法不需要检测偏移距离d,而是离线建立了TensorFlow神经网络负载与互感识别模型,通过设置不同的偏移距离d和传输距离h得到互感M的训练数据,再将训练数据输入模型进行离线训练,训练完成后将识别模型导入控制器进行在线识别。在线识别时,只需要检测输入电流值Iin和传输距离h,调用识别模型计算得到负载与互感值;通过系统建模分析,给出了负载与互感识别模型设计的方法和步骤,通过仿真验证了该方法的可行性。在实验中,通过调整线圈相对位置和负载电阻改变系统互感和负载大小,在微型控制器中调用TensorFlow神经网络负载与互感识别模型进行在线识别。仿真和实验结果表明,本文提出的基于TensorFlow神经网络的负载与互感识别方法比以往的负载与互感识别方法精度有较大提升,识别速度也有所提升,并能适应较大的负载与互感变化范围,且易于实现、成本较低,更有利于工程推广应用。
需要指出的是,本文所提出的方法主要针对无磁芯的耦合机构。针对耦合机构有磁芯的MCRWPT系统的负载与互感识别方法值得进一步研究。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx),扫英文摘要后二维码可以阅读网络全文。
