用于多交流系统耦合下MMC-HVDC稳定性分析的模块化阻抗建模方法

高 剑, 朱 童, 杜程茂, 杜 雄, 张 博, 李 甘, 叶 希, 聂鸿宇, 应林志

(1. 国网四川省电力公司, 四川 成都 610041; 2. 输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆 400044)

1 引言

基于模块化多电平换流器的高压直流输电(Modular Multilevel Converter-based High Voltage Direct Current, MMC-HVDC)具有输出电能质量高、占地面积小以及可靠性高等优势,如今已成为大规模、远距离风电送出或异步电网互联等场景的理想解决方案[1-3]。然而,国内外多个实际工程事故表明,MMC换流站与新能源发电/交流电网等交流系统之间动态交互存在振荡风险,严重制约了风电的安全可靠消纳,削弱了电网稳定运行能力[4,5]。因此迫切需要对多交流系统耦合的MMC-HVDC直流电网系统进行稳定性分析。

时域特征值法和频域阻抗分析法是目前评估系统小信号稳定性的主流分析方法[6]。时域特征值法不仅可以判断系统的小信号稳定性,还可以获取系统振荡频率、模态阻尼、稳定裕度等量化信息[7,8]。然而,特征值法依赖于全局状态空间方程,在装备众多的复杂系统分析中存在高阶模型求解困难的问题,这对于多交流系统耦合的MMC-HVDC的振荡风险评估是较大的挑战[7]。

频域阻抗分析法具有物理意义清晰、容易测量的优势,可表征装置/系统的端口宽频特性。直接采用经典控制理论中的Bode图、Nyquist判据等经典判据可简单有效地分析互联系统的稳定性。通过计算基于阻抗比的等效开环传递函数的特征值仍然可以实现阻尼和振荡频率的量化评估[9]。此外,IEEE PES风能次同步振荡工作小组报告中指出,阻抗分析方法已经广泛应用于风电并网系统的稳定性分析[10]。因此,合理建立子系统频域端口阻抗模型是稳定性分析的关键。

MMC换流器是一个包含多时间尺度动态特性、多谐波耦合、强非线性的电力电子装置,基于谐波平衡和小信号近似的多谐波线性化(Multi-Harmonic Linearization,MHL)阻抗建模方法可有效表征MMC的多谐波耦合特性,在文献[11]中被提出且已在不同MMC应用场景中得到了推广应用[12-18]。文献[12,13]考虑双闭环交流电压控制建立了送端MMC换流站的阻抗模型,但未考虑风场交流系统与MMC换流站之间耦合作用。文献[14]考虑桥臂谐波动态,建立受端MMC换流站的直流侧阻抗模型,但未计及与电网之间的频率耦合效应。文献[15]揭示了MMC与交流电网之间的频率耦合机理,提出了考虑频率耦合的整体建模方法,同时考虑直流电压外环、功率外环、锁相环等多时间尺度控制的影响,建立了受端MMC的等效阻抗模型。采用该方法,考虑频率耦合的多落点MMC换流站的等效阻抗模型在文献[16]中被提出,但以上模型均忽略了送端MMC换流站的影响。文献[17,18]考虑以双端MMC-HVDC为研究对象,考虑受端MMC的影响,建立了送端MMC交流侧阻抗模型,并评估了风场接入的振荡风险,然而该建模过程并未清晰指出如何考虑非理想电网的影响。采用忽略了交流系统接入的频率耦合特性的简化阻抗模型可能得到不准确的分析结果[15]。文献[11-18]建立了不同场景下的MMC-HVDC阻抗模型,对MMC-HVDC稳定性分析起到了一定的推动作用,然而多交流系统耦合的MMC-HVDC直流电网是未来发展趋势,目前研究尚未理出一套合理有效的阻抗建模思路,不利于未来MMC-HVDC系统振荡风险评估与振荡抑制。

针对这一问题,本文提出一种基于“子系统划分-交流系统阻抗提取-直流端口阻抗等效与聚合”的模块化建模思路。首先根据稳定性分析需求进行子系统划分,然后采用多谐波建模方法提取各装备的频域阻抗特性,最后通过阻抗聚合建立端口等效阻抗模型。搭建了基于Matlab/Simulink的MMC-HVDC四端系统电磁暂态(ElectroMagnetic Transient, EMT)仿真平台,对建模方法的有效性和分析结果的正确性进行了验证。

2 模块化阻抗建模方法

本节将根据交流系统与MMC换流站之间的耦合作用,同时考虑直流电网中直流母线的动态耦合,提出一种适用于多交流系统耦合的MMC-HVDC的“子系统划分-交流系统阻抗提取-直流端口阻抗等效与聚合”的建模思路。

2.1 多交流系统耦合的MMC-HVDC系统

多交流系统耦合的MMC-HVDC系统架构如图1所示。新能源发电如风电、光伏等,以及传统发电如水电、火电均可以通过送端MMC接入到直流电网中,经远距离直流输电线路传输至受端MMC换流站,向远距离负荷中心供电或者实现异步电网互联。值得注意的是,送端也可能是风光互补、“风火打捆”等多种混合发电方式。

图1 多交流系统耦合的MMC-HVDC构架Fig.1 MMC-HVDC architecture with multi-AC system coupling

图1中,MMC-HVDC的送端换流站和受端换流站均与交流系统相互耦合。建立多交流系统耦合下MMC-HVDC阻抗模型是一项亟需开展的工作,目前针对MMC-HVDC系统阻抗建模或稳定性分析大多忽略了多交流系统与直流输电之间的耦合作用。因此,本文将提出考虑各个交流系统耦合特性实用的建模方法。

2.2 多交流系统耦合的阻抗建模方法

基于阻抗的分析方法是将互联系统划分为两个子系统,通过判断两个子系统的阻抗比是否满足Nyquist判据以评估系统稳定性。因此建立端口划分处子系统的阻抗模型是准确分析互联系统稳定性的前提。“子系统划分-交流系统装备阻抗提取-直流端口阻抗等效与聚合”的建模思路如下:

(1)子系统划分。确定需要重点关注的某个或某些装置接入直流电网的稳定性,在实际系统结构划分子系统。以图1为例,考虑第n个MMC接入直流网络的稳定性,从端口n将直流电网划分为子系统①和子系统②。

(2)交流系统模块化阻抗建模。采用多谐波线性化的建模方法建立各交流系统的阻抗矩阵模型。可以用阻抗矩阵统一表示:

(1)

考虑多输入多输出特性(Multiple Input and Multiple Output, MIMO)[15],阻抗矩阵Zac可以表示光伏、风电等电力电子设备的阻抗特性。式(1)中fp和f0分别为扰动频率和基波频率;下标“p”和“n”分别表示正序和负序;阻抗Znn为fp-2f0频率的负序扰动电压和fp-2f0频率的负序扰动电流之间的关系,阻抗Zpn为fp-2f0频率负序扰动电压与fp扰动频率正序电流之间的关系,Znp和Zpp与此类似。当交流系统为单输入单输出网络或非电力电子装备时,式(1)中矩阵元素Znp与Zpn应被置零。

(3)MMC直流侧阻抗模块化建模与聚合。交流系统之间或交流系统与MMC换流站之间的交互耦合是导致阻抗建模难的关键[15,16]。为方便叙述,以图2中四端MMC-HVDC直流电网为例,交流系统1和2通过传输线相互耦合,可以采用Y-Δ变换对交流网络进行等效转换并解耦。其次,为考虑交流系统与MMC之间耦合的影响,将解耦后的交流系统阻抗视为MMC换流站阻抗的一部分,建立其整体的频域主电路模型:

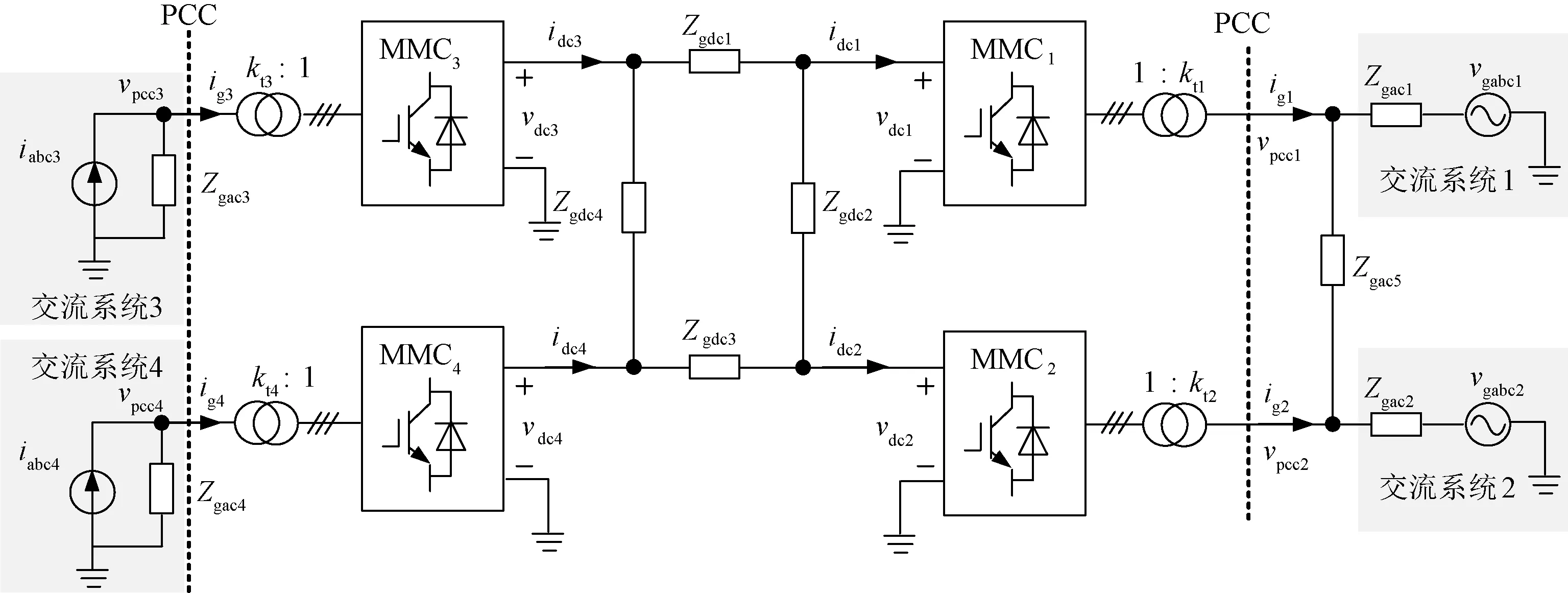
图2 四端MMC直流输电网络结构Fig.2 Power circuit of four-terminal MMC-HVDC transmission system

(2)

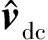
3 MMC-HVDC四端直流电网阻抗建模

本节以四端直流输电系统为例说明并验证所提建模方法的有效性。四端MMC直流网络结构如图2所示。在直流侧,四座换流站并联构成一个直流环形网络,Zgdc1、Zgdc2、Zgdc3、Zgdc4为直流线路阻抗。在交流侧,每座换流站通过变压器接入公共并网点(Point of Common Coupling, PCC),Zgac1、Zgac2、Zgac3、Zgac4和Zgac5为交流线路阻抗。图2中,iabc3、iabc4分别为交流系统3和交流系统4的等效电流源;vpcc1、vpcc2、vpcc3和vpcc4为换流站接入交流系统PCC点的电压;ig1和ig2分别为MMC1和MMC2经变压器接入交流系统的电流;ig3和ig4分别为交流系统3和交流系统4馈入直流电网的电流。

MMC换流站的控制策略如图3所示。换流站内环控制器均包含电流环内环控制和环流控制。而MMC的外环因换流站的控制需求不同而不同。MMC1和MMC2为受端换流站,控制结构如图3(a)所示。其中MMC1采用定直流电压控制和无功功率控制,维持直流网络电压稳定,此时控制选择开关置于“1”处。MMC2采用定有功和无功功率控制,分配换流站之间的传输功率,此时控制选择开关置于“2”处。图3(a)中,Pr、Vdcr和Qr分别为有功功率参考、直流电压参考以及无功功率参考;HP(s)、HVD(s)和HQ(s)分别为有功PI控制器、直流电压PI控制器和无功PI控制器;Hi(s)和Ki分别为电流内环PI控制器和解耦系数;θ为锁相环的输出相位;igd和igq为转换至dq轴系下的并网电流;ma、mb和mc分别为静止坐标系下a相、b相和c相投切系数。此外,MMC1和MMC2采用图3(b)所示的锁相环(Phase Locked Loop,PLL)跟踪电网电压的相位。图3(b)中vpcc为换流站的交流侧PCC点电压;vd和vq为经dq变换后的PCC点电压;Hpll(s)为锁相环PI控制器。

图3 四端直流输电系统控制环节示意图Fig.3 Schematic diagram of control loops of four-terminal MMC-HVDC transmission system

MMC3和MMC4为送端换流站,均采用定交流电压控制,为新能源发电基地提供电压和频率支撑,控制结构如图3(c)所示。图3(c)中,Vdr和Vqr分别为交流电压的d轴和q轴参考值;HVA(s)为交流电压PI控制器。各换流站均采用如图3(d)所示的环流控制以抑制二倍基频的负序分量,其中icdr和icqr为环流参考值;Hic(s)和Kic分别为环流PI控制器和解耦系数;icd和icq分别为d轴桥臂环流分量和q轴桥臂环流分量;msa、msb和msc分别为静止坐标系下控制器最终输出的a相、b相和c相投切系数。系统参数见表1,如无特殊说明本文的仿真验证和稳定性分析也采用此参数。

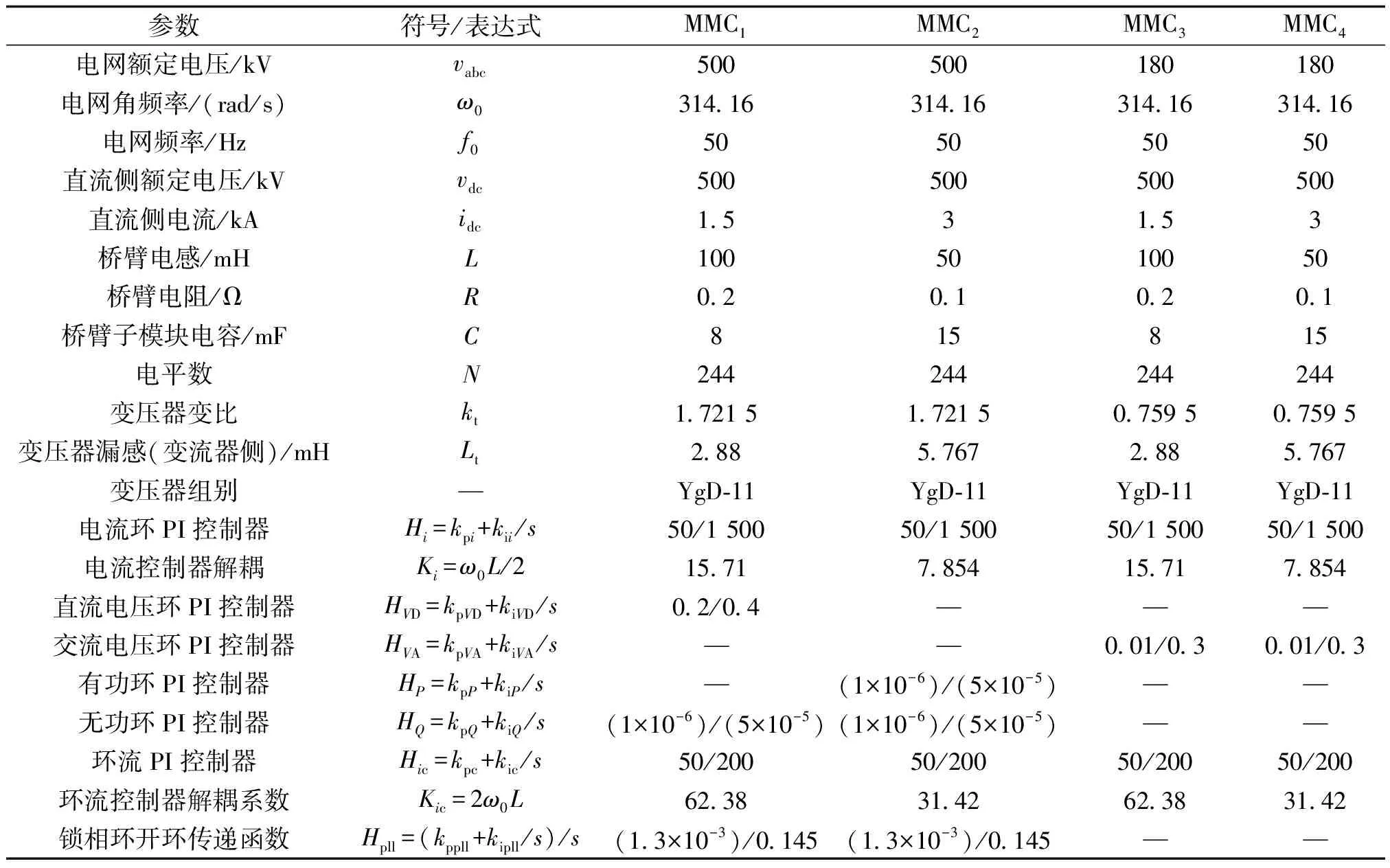
表1 四端直流输电系统仿真参数Tab.1 Simulation parameters of four-terminal MMC-HVDC transmission system

已有大量文献针对独立交流系统阻抗模型进行了推导与分析,本文不再赘述。接下来考虑交流系统耦合的影响,采用多谐波线性化的方法,建立定直流电压控制(MMC1)、定功率控制(MMC2)和定交流电压控制(MMC3和MMC4)MMC换流站的模块化直流侧阻抗模型。

3.1 MMC换流站直流侧阻抗建模

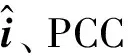
(3)

(4)

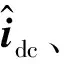
(5)

式中,Ta用于表示注入扰动后三相变量与上、下桥臂变量关系:

Ta=diag[(-1)S2,n]

(6)

式中,辅助函数S2,n用以描述桥臂变量和三相变量的差模输出和共模环流属性:

(7)

式中,n为稳态谐波次数,本文考虑3次谐波(n=3)的影响进行阻抗建模。由式(2)～式(5)可以得到并网MMC主电路频域模型线性化模型如式(8)所示。

(8)

(9)

式中,Δi、Δic、ΔVD、ΔVA、ΔP、ΔQ、Δpll分别为电流环、环流控制、直流电压控制、交流电压控制、有功功率控制、无功功率控制和锁相环扰动对投切系数的影响。环流控制对投切系数的关系可表示为:

(10)

其中

(11)

式中,kpc和kic分别为PI控制器的比例系数和积分系数;ω0和L分别为电网角频率和桥臂电感。辅助函数S1,n用以描述各变量的相序特性:

(12)

电流控制内环对投切系数的关系可表示为:

(13)

其中

(14)

电流参考值对投切系数的传递矩阵为:

(15)

式中,kt为MMC换流站交流侧与交流系统之间的变压器变比。

由于外环通过控制电流环给定影响投切系数,交流电压控制和投切系数的关系可表示为:

(16)

其中

(17)

式中,kpVA和kiVA分别为交流电压PI控制器的比例系数和积分系数。

直流电压控制和投切系数的关系可表示为:

(18)

由于直流电压外环控制仅作用于零序环流分量,因此直流电压控制传递矩阵GVD中仅含GVD(3,4)和GVD(4, 4)两个非零元素:

(19)

式中,kpV和kiV分别为直流电压PI控制器的比例系数和积分系数。

变流器功率扰动可以由桥臂电流和交流电压扰动表示为:

(20)

式中,VP、VQ分别为有功环和无功环的交流电压稳态谐波矩阵;IP、IQ分别为有功环和无功环的桥臂电流稳态谐波矩阵。可以得到有功和无功功率对投切系数ΔP和ΔQ的影响如下:

(21)

与GVD类似,控制矩阵GP和GQ中的非零元素可以表示如下:

(22)

(23)

锁相环对投切系数的影响Δpll可表示为:

(24)

(25)

(26)

式中,Iu,n、Mu,n分别为稳态矩阵中对应的桥臂电流和投切系数n次谐波稳态分量;Hi,1为式(15)的控制矩阵中fp+f0频率对应的电流控制传递函数;Tpll,n为锁相环的闭环传递函数:

(27)

式中,Hpll,n为锁相环的开环传递函数;V为PCC点电压幅值。

(28)

(29)

式中,Ei、Ev分别为桥臂电流和直流侧电压对投切系数的影响,其取值随MMC控制策略变化而变化。对于定直流电压控制和无功功率控制的MMC1:

(30)

Ev=GirGVD

(31)

对于定有功功率控制和无功功率控制的MMC2:

(32)

Ev=0

(33)

对于定交流电压控制的MMC3和MMC4:

(34)

Ev=0

(35)

(36)

Ydc中心元素的倒数即为考虑了变压器影响的MMC直流侧的阻抗特性ZMMC(fp)。式(36)中,Bi、Bv分别为直流电流扰动和直流侧电压扰动对直流侧阻抗的影响:

(37)

Bv=YL[0.5U-(Vu+MuZCIu)Ev]

(38)

在Matlab/Simulink中分别搭建三种不同控制器下的MMC仿真模型,在直流端口注入频率为fp的小扰动信号,测量fp频率下输出信号的幅值和相位信息,通过电压和电流的比值就可以得到变流器在该频率下的阻抗,通过改变频率fp分别得到三种不同控制器MMC直流的阻抗曲线,如图4所示。实线代表所建立的解析模型,点线代表仿真扫描的结果,验证了建立MMC直流端口阻抗模型ZMMC(fp)的正确性。由于MMC3和MMC4采用同样的控制方式,本文以MMC4的参数进行验证。

图4 直流侧阻抗模型验证Fig.4 DC side impedance models validation

3.2 交流系统解耦与直流侧阻抗聚合

对于四端环形直流输电系统,受端换流站之间交流侧和直流侧电网均存在耦合,如图5(a)所示。需要对模型进行等效解耦后再进行稳定性分析,如图5(b)所示。

图5 交流系统解耦方法Fig.5 AC system decoupling method

先对受端交流系统进行解耦,受端交流系统可以等效为图5(c)所示。再通过式(39)可以进一步等效为图5(d)。

(39)

式中,Zy1、Zy2与Zy3为图5(c)经过Y-Δ转换得到的Y型网络阻抗值。

引入系数k1和k2对公共电网阻抗Zy3进行解耦,得到等效电网阻抗Zeq1和Zeq2,如图5(e)所示。

(40)

式中,系数k1和k2由MMC1和MMC2的并网电流ig1和ig2决定。

(41)

当四个换流站交流侧相互独立后,再对直流网络进行等效聚合。模型四端MMC直流阻抗网络拓扑如图6(a)所示,输电线路采用虚线框中的π型结构等效。以Zgdc1为例,Z12和Z13为线路的对地电容阻抗,Z1包括直流线路阻抗和平波电抗器阻抗。其他三条线路同理,阻抗取值见表2。ZMMC1、ZMMC2、ZMMC3、ZMMC4分别为第3节建立的各个换流站直流侧阻抗。将图6(a)中电流源和电压源支路分别等效为开路和短路,可得图6(b)所示的等效直流网络。将图6(b)中虚线框中阻抗聚合得到图6(c)中阻抗Za、Zb和Zc。进一步对阻抗Z3、Zb和Z4进行如图5所示的Y-Δ变换,并于Za、Zb聚合可以得到图6(d)等值网络中的阻抗Zd、Zf和Ze。类似地,经过多次Y-Δ变换与阻抗聚合即可得到图6(e)所示的子系统端口等值阻抗,此时已将直流环网等效为MMC1换流站直流侧阻抗ZMMC1和直流电网等效阻抗Zdcg,eq两部分。

表2 交直流线路参数Tab.2 AC and DC line parameters

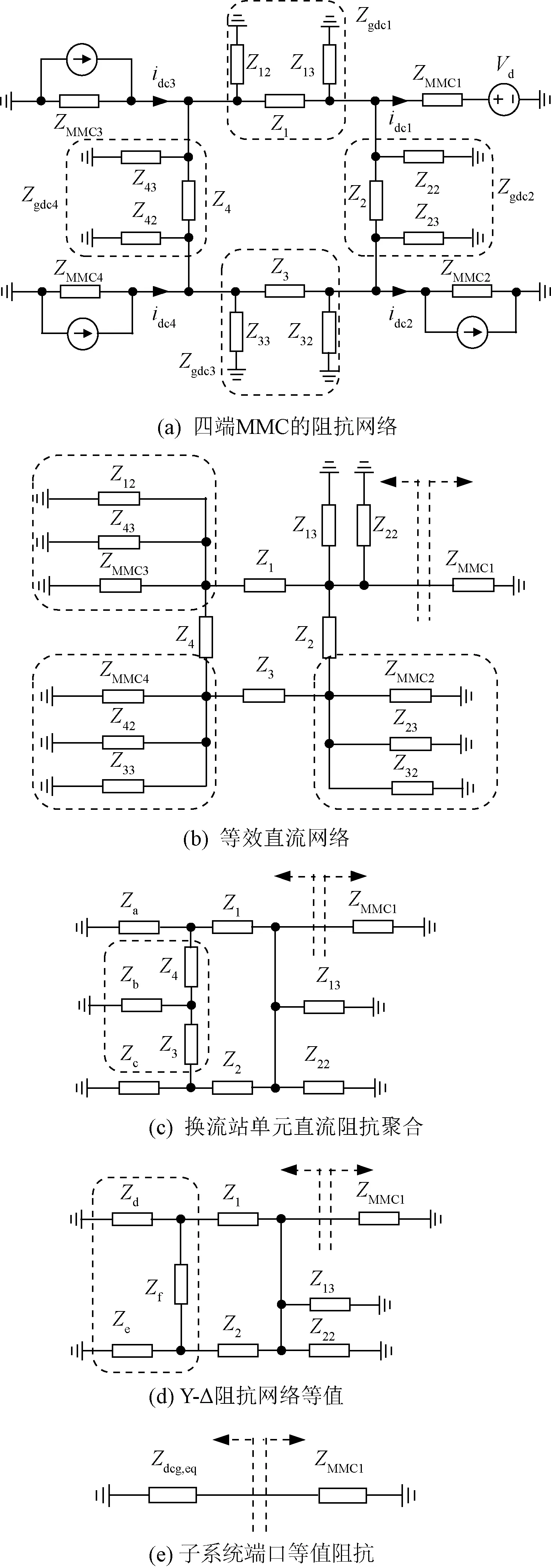
图6 直流阻抗网络等效与聚合Fig.6 DC impedance network equivalence and aggregation

4 MMC-HVDC四端直流电网稳定性分析

对解耦等效后的四端MMC-HVDC模型进行稳定性分析。交直流线路参数见表2。根据式(39)～式(41)和MMC1、MMC2的并网电流计算得到等效电网阻抗分别为Zeq1=0.691+0.1s、Zeq2=1+0.101s。再根据第3节求出各MMC换流站直流侧端口阻抗。此时,直流网络中各个换流站交流侧独立,同时能够稳定运行。采用图6所示的方式对直流环网进行等值聚合,得到ZMMC1和Zdcg,eq两部分阻抗,即可进行稳定性分析。

绘制ZMMC1和Zdcg,eq的幅频特性、相频特性曲线如图7所示。图7(a)展示了MMC1直流电压外环参数为0.005/0.02时的Bode图。两条阻抗的幅频曲线有4个交点,分别为20 Hz、22 Hz、25 Hz、92 Hz。由对应的相频特性可知在这些频率下它们的相位裕量均大于0,预示着互联系统稳定。

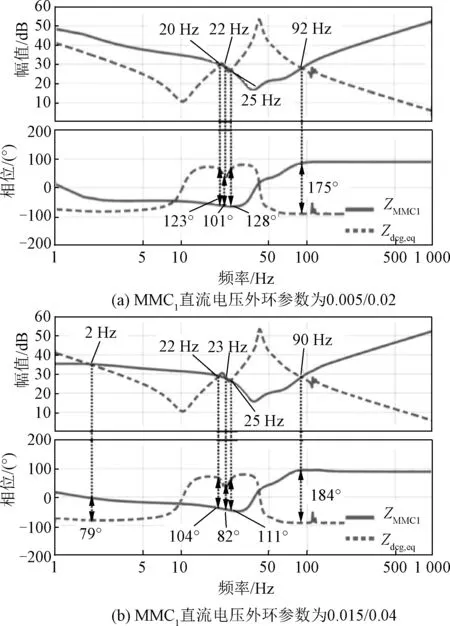
图7 ZMMC1和Zdcg,eq的阻抗特性曲线Fig.7 Impedance characteristic curves of ZMMC1 and Zdcg,eq

MMC1直流电压外环参数为0.015/0.04时的Bode图如图7(b)所示,幅频曲线存在5个交点,分别为2 Hz、20 Hz、23 Hz、25 Hz、90 Hz。其中2 Hz、20 Hz、23 Hz、25 Hz对应的相位裕量大于0,而90 Hz对应的相位差为184°,即相位裕量为-4°,预示着互联系统将产生90 Hz左右的振荡。

在Matlab/Simulink中搭建该四端MMC-HVDC输电系统模型,对图8的分析结果进行验证,如图8所示。在15 s前,MMC1直流电压外环参数为0.005/0.02时,系统稳定性运行。在15 s时,参数变为0.015/0.04,系统发生振荡。对MMC1的直流侧端口电压进行快速傅里叶变换分析,发现存在91 Hz的谐波,验证了稳定性分析的正确性。

图8 直流端口电压时域仿真结果Fig.8 Time domain simulation results of DC port

5 结论

针对多交流系统耦合下MMC-HVDC阻抗建模这一问题,本文提出一种“子系统划分-交流系统阻抗提取-直流端口阻抗等效与聚合”的模块化建模思路。以四端MMC-HVDC为研究对象,采用多谐波线性化的方法建立了MMC的直流阻抗模型。考虑了交流系统耦合对MMC直流阻抗特征的影响,提高了建模的准确性。同时,针对换流站间交流和直流侧均存在电气联系的情况,提出一种针对换流站间交流侧解耦方法,能够有效实现网络的解耦计算,搭建了基于Matlab/Simulink的四端MMC-HVDC直流电网EMT平台,仿真结果验证了建模方法的有效性和分析结果的正确性。本文的研究内容可为MMC-HVDC直流网络振荡预测和参数设计的研究提供理论依据。