计及电解铝负荷需求侧响应的风电并网调峰研究

张 斌, 司大军, 李 凡, 何金定, 剡文林, 牛 涛

(1.昆明理工大学国土资源工程学院, 云南 昆明 650093; 2.云南电网有限责任公司, 云南 昆明 650011; 3.重庆大学电气工程学院, 重庆 400044)

1 引言

近年来,随着世界各国对于环境保护问题的广泛关注,增加风电、光伏等新能源的装机容量成为了解决环境污染和化石能源不足等问题的主要方法[1,2]。然而,风电等新能源的并网也为电网的调峰提出了更高的要求。由于风电的出力具有明显的不确定性、波动性和反调峰特性,往往使得电网的下调峰能力不足,造成严重的弃风现象[3-5]。相较于安装储能设备调峰等手段,发掘负荷侧的调度潜力,通过需求响应措施引导用户调整用电行为,避免了沉重的经济投入和冗长的建设周期,是一项经济可行的方法。

当前,已有众多学者围绕不同类型负荷、不同响应方式展开了研究,并取得了一定的成果。其中,文献[6]中讨论了多类型柔性负荷的调度作用,说明柔性负荷能够有效改善电网电能供给压力;文献[7,8]建立了一种通过负荷对电价的响应参与系统调节的负荷调度方案,显著提高了负荷侧响应并参与电力系统经济调度的积极性;文献[9]则从市场角度分析了大工业负荷在电网调节中能够起到的作用;文献[10]综合考虑计算效率、实时电价信息和电网调度需求,分别设计了集中式和分布式协同调度框架。上述文献大多只考虑了电网侧与负荷侧的协调调度策略,忽略了企业和用户侧的生产隐私性。

在众多可调度柔性负荷中,以高载能企业为代表的大工业负荷的调度潜力最为巨大。考虑到我国西北地区和西南地区具有丰富的风电、水电资源和众多高载能企业的情况,若能将高载能负荷纳入调峰体系中,通过激励机制引导其参与新能源消纳,能够有效地缓解电网的调峰压力[11]。电解铝、水电硅等高载能负荷具有用电量大、用电成本占总生产成本比重高、自备电厂易于连续调节等特点,具有可观的调度潜力。当前已有学者围绕着电解铝负荷建模和用电行为刻画展开研究。文献[12]建立了电解铝负荷的运行-停运数学模型,对电网和负荷的调度计划进行迭代优化求解;文献[13]对于电解铝企业的生产流程进行了研究分析,建立了企业内部每一生产阶段详细的数学模型;文献[14]详细建立了电解铝负荷与风电交互的控制模型,但该模型过于复杂,难以计算。

同时,为引导负荷侧参与调峰,电网侧通常会制定一些经济补偿措施和电价优惠策略,引导企业侧自主调节出力。文献[15]提出提高峰时电价的方法,对在高峰时期持续用电的企业进行惩罚,并将惩罚所得补偿给在该时段内减少用电的用户,这在一定程度上增强了系统的调峰能力。文献[16,17]以电网收益最大化为目标,调整峰谷电价,在不同的电价方案下制定多种用户补偿曲线,并从中求得最优解。

综上所述,只有建立详细的电解铝负荷数学模型,设计合理可行的电解铝企业参与电力系统调峰的机制,在保证电解铝企业生产隐私的前提下,考虑多电解铝企业间的竞争关系和议价能力,合理分配协同调度利益,电解铝企业才有足够的积极性参与系统调峰,实现多方共赢。

2 风电并网对调峰的影响

2.1 风电出力特征分析

(1)随机性:由于天气等环境因素的影响,风电机组的出力具有很强的随机性。在一年中的不同时间内,风电机组的出力可能接近于0,也可能接近于额定功率,难以准确预测。

(2)波动性:在同一天中,风电的出力也具有明显的波动性,相邻时段内的出力会产生大幅的变化。

(3)反调峰性:在对风电并入电网后的特性进行研究时,通常将风电的出力看作负荷,与电网的常规负荷相叠加,最后得到一个等效负荷。风力资源的大小情况与实际负荷的峰谷情况在时间上通常是相反的,即风力资源在夜间较为丰富,电网负荷需求大多集中在白天。因此在大量风电并网后,电网等效负荷的变化趋势会变得更加陡峭,削弱了电网的调峰能力,这种特性被称作反调峰特性。

2.2 风电并网调峰需求分析

图1展示了风电并网对电网调峰需求的示意图。通常情况下,系统的负荷在夜晚时间段内较低,电网能够通过关闭机组或者减小机组出力以维持系统功率平衡。但是,当风电机组大量接入电网后,其反调峰特性的存在会导致系统在夜间的等效负荷进一步降低,而电网常规机组存在调峰下限的约束,因此仅通过调节常规机组的出力无法保证源荷功率的平衡。为了使得系统可以稳定运行,需要通过增加弃风量来维持系统功率的平衡,这造成了风电资源的极大浪费。

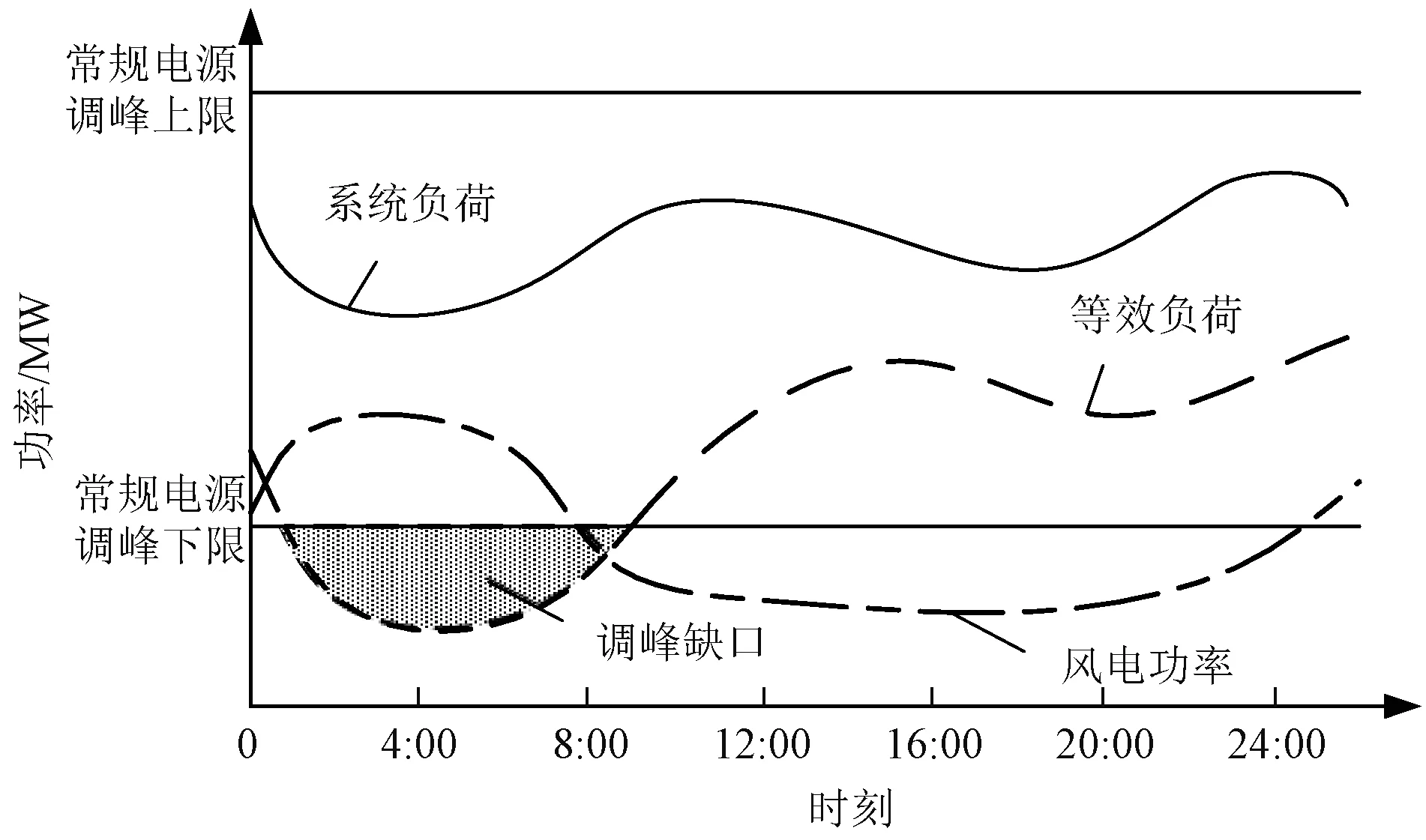
图1 风电并网对电网调峰需求Fig.1 Wind power grid-connected demand for grid peak regulation

3 电解铝负荷-电网协同调度模型

3.1 电解铝负荷生产模型

对于电解铝负荷来说,其数学模型主要包括两部分—电解槽生产模型和自备电厂机组出力模型。通过调整电解槽功率和自备电厂机组出力,响应系统侧的调峰指令。电解槽生产模型主要包括功率约束、功率爬坡约束、调节时间约束和产量约束,具体的数学表达如式(1)～式(4)所示。

电解槽功率上下限约束:

Pload,min,j≤Pload,j,t≤Pload,max,j

(1)

式中,Pload,min,j和Pload,max,j分别为第j台电解槽生产所允许的最小功率和最大功率;Pload,j,t为第j台电解槽在t时刻的实际功率。

电解槽功率爬坡约束:

Rload,down≤Pload,j,t-Pload,j,t-1≤Rload,up

(2)

式中,Rload,down、Rload,up分别为电解槽的爬坡功率下限和上限。负荷功率调节爬坡约束表示电解铝生产过程中负荷功率调整速率约束。

由于铝电解槽的频繁调节会导致槽内氧化还原反应不稳定,最终影响产品的质量。为此,本文设置电解槽调节时间约束:

(3)

式中,Zj,t为t时刻第j台电解槽功率调整标志位,当其取值为1时,表示在此时刻电解槽功率进行了调整,当其取值为0时,表示此时刻的电解槽功率维持不变;Tj,on为维持第j台电解槽的功率保持不变的最小时间;M为一个数值很大的常数;T为调度的总小时数。

产量约束:

(4)

式中,J为电解铝厂内电解槽个数;EN为产量最小要求;k为吨铝能耗值,这里取值为12.75 MW/tAl。

为了降低生产成本,电解铝企业往往建有自备电厂。自备电厂中的机组出力模型与电力系统机组组合模型类似,需要考虑自备电厂机组出力约束、机组出力爬坡约束、购售电功率传输约束和功率平衡约束。

自备电厂机组出力约束:

ugen,iPgen,min,i≤Pgen,i,t≤ugen,iPgen,max,i

(5)

式中,Pgen,min,i、Pgen,max,i分别为自备电厂中第i台机组的最小和最大出力限制;Pgen,i,t为自备电厂中第i台机组的实际出力;ugen,i为第i台机组启停状态的0、1变量,当其取值为1时,表示机组处于运行状态;当其取值为0时,表示机组处于停运状态。

自备电厂机组出力爬坡约束:

Rgen,i,down≤Pgen,i,t-Pgen,i,t-1≤Rgen,i,up

(6)

式中,Rgen,i,down、Rgen,i,up分别为自备电厂中第i台机组的爬坡下限和上限。

购售电功率传输约束:

(7)

式中,Pbuy,t、Psell,t分别为电解铝企业在t时刻从电网中的购电量和售电量;Ptie为联络线允许传输的功率最大值。

功率平衡约束:

(8)

式中,I为自备电厂中机组的个数;xt为购售电的状态标志位,当其取值为1时,表示电解铝厂从电网中购电,当其取值为0时,表示电解铝厂向电网中售电。本文中购电和售电状态不能同时发生。

3.2 电网侧调度模型

在包含电解铝企业的电网日前调度中,需考虑系统中发电机的出力约束、发电机出力爬坡约束、源荷不确定性约束、功率平衡等约束。

发电机组出力约束:

uGEN,tPGEN,min,j≤PGEN,j≤PGEN,max,juGEN,i

(9)

式中,PGEN,j为电力系统中第j台机组的实际出力;PGEN,min,j、PGEN,max,j分别为发电机j允许的最小和最大出力;uGEN,t为电网中机组状态标识符,具体定义方式与式(5)类似,这里不再详细阐述。

发电机组出力爬坡约束:

RGEN,down,j≤PGEN,j,t-PGEN,j,t-1≤RGEN,up,j

(10)

式中,RGEN,up,j、RGEN,down,j分别为机组j的爬坡上下限。

由于风电出力和负荷用电功率的不确定性,很难写出准确的功率平衡约束和旋转备用约束。为此,本文采用模糊机会约束刻画源荷双端的不确定性。风电出力和负荷用电功率的模糊参数对于原出力模糊集的隶属函数可使用梯形函数来表示,具体的数学表达如下所示:

(11)

式中,PWG1、PWG2、PWG3、PWG4为隶属度参数,可根据式(12)计算得到:

PWGi=wiPpre

(12)

式中,wi为比例系数,具体值可根据风电出力以及负荷功率的历史数据来确定;Ppre为风电机组或负荷功率的预测值。引入借助模糊数学理论中的清晰等价类条件,可以将系统的功率平衡约束和旋转备用约束等价写成式(13)、式(14)。

(13)

(14)

式中,NGEN为全体高载能企业自备机组集合;D为系统中除电解铝企业外其他负荷节点个数;PWind,t为t时刻系统中风电的出力;Pd,t为t时刻系统中负荷节点d的功率;a为置信度。

3.3 协同调度框架设计

电解铝企业作为高载能企业,其产量、生产信息和成品售价属于企业隐私,因此其自备电厂和发电负荷一般不直接接入电力系统控制中心,电力系统无法直接控制电解铝负荷。为了高效协调电解铝负荷-电网,本文设计了多级信息交互系统。在第一阶段,电网侧根据风电的预测出力和负荷的预测功率,以弃风量最小为目标,计算得到需要电解铝企业协助消纳的电量信息,并将此电量信息发送给参与响应的各电解铝企业;然后,借鉴鲁棒优化的思想,引入功率松弛因子v+和v-,将功率平衡方程式(8)松弛为式(15)所示形式。

(15)

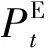
(16)

当接收到电解铝企业反馈功率松弛因子的值后,电网侧进行相应的发电计划调整。具体地,当反馈的v+和v-的数值为0时,表示电解铝企业可以完全响应电网侧发送的购售电功率调整指令;当v+的值为正时,表示电网侧发送的购售电功率调整值太大,电解铝企业无法实现,需要电网调度中心在期望购售电信息的基础上减去v+的值;v-的值非零时,电网侧的处理方法类似。

另一方面,电解铝企业属于典型的利益驱动型企业,当引导其参与电力系统调峰时,需要给予一定的经济激励。考虑到我国对新能源发电的补贴,电解铝企业参与新能源消纳后,电网的经济收入增加,可将此部分新增的经济收入作为电网-电解铝企业的利益分配对象。本文采用纳什合作博弈模型式(17)、式(18)进行利益分配。

(17)

(18)

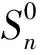
4 算例验证

为了说明本文所提方法的有效性和可行性,本文采用改进的IEEE-30节点测试系统进行算例验证,系统中接入两个电解铝企业,其中电解铝企业1接在节点3处,电解铝企业2接在节点21处。每个电解铝企业均由一个电解槽和一个自备电厂构成,自备电厂中包含两台发电机组,联络线传输功率最大值为180 MW。电解铝企业详细的设备和分时电价信息见表1～表3。模糊参数的选取见表4。模糊机会约束的置信度a取值为0.6。

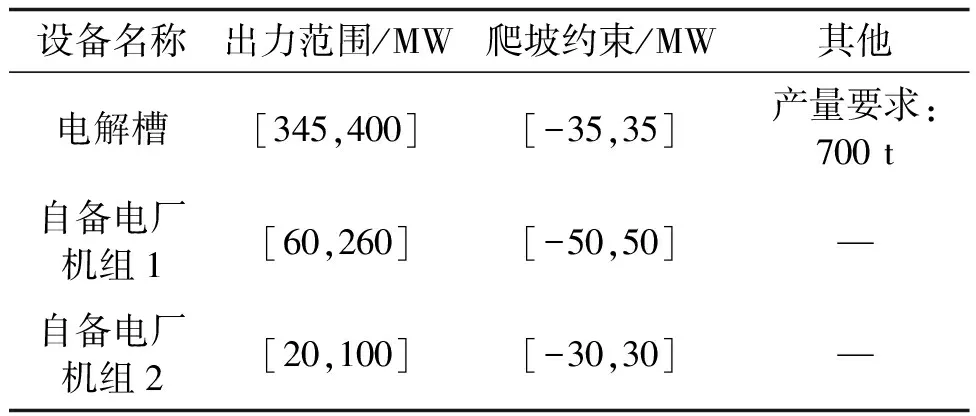
表1 电解铝企业1的详细信息Tab.1 Details of electrolytic aluminum enterprise 1

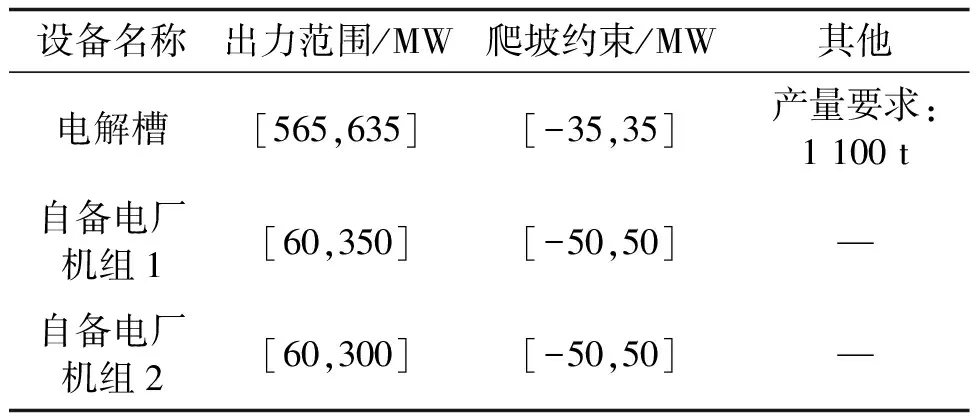
表2 电解铝企业2的详细信息Tab.2 Details of electrolytic aluminum enterprise 2

表3 分时电价信息Tab.3 Time of use price information

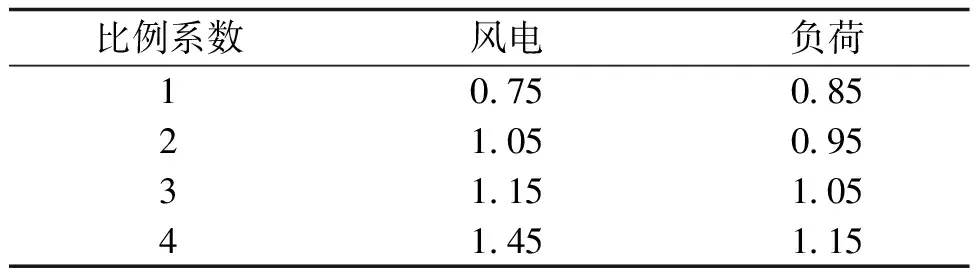
表4 模糊参数信息Tab.4 Fuzzy parameter information

同时,为了更加直观地说明,本文设置了两个场景进行对比:场景1:初始场景下,电解铝企业仅根据分时电价,以生产用电成本最小为目标制定购售电计划和自备电厂出力方案。场景2:协同调度场景下,电解铝企业按照本文所提方法展开调度。

4.1 电解铝企业用电行为分析

图2展示了两个场景下电解铝企业的购电信息。在初始场景下,电解铝企业在电价低的时段从电网中购电,在电价高的时段减少购电量。同时,由于风电出力的波动性,可以发现协同调度下的电解铝企业的购售电曲线调整更加频繁,实现快速跟踪风电出力变化,协助系统消纳风电。

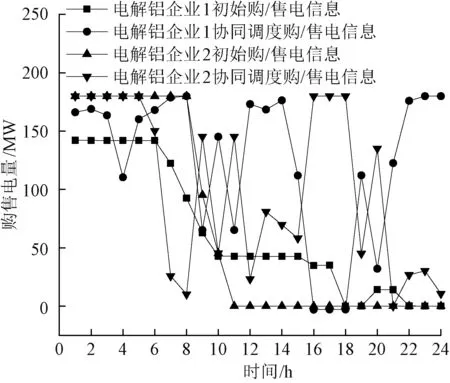
图2 不同场景下电解铝企业购售电曲线对比Fig.2 Comparison of purchase and sale curves of electrolytic aluminum enterprises under different scenarios

图3展示了企业内部自备电厂和电解槽的功率变化情况。观察图3(a)和图3(b)可知,电解铝企业增加了在风电出力较大时段或者本地其他负荷用电功率较小时段的购电量。在分时电价下,电解铝企业内部的电解槽的功率调整次数较少,同时在低电价的凌晨时段,电解铝企业将生产任务集中在此时段,电解槽维持在较高功率水平,实现低成本生产。但是不容忽略的是,分时电价作为一种静态的电价机制,无法有效反映每时刻的风电-负荷供需信息,导致电价信息与风电出力信息不匹配,在某些严重情况下,甚至会出现电价高的时段大量风电由于系统调峰能力不足而白白浪费的现象。

图3 不同场景下电解铝企业设备功率对比Fig.3 Comparison of equipment power in electrolytic aluminum enterprises under different scenarios

本文中提出的电网-多电解铝企业协同调度模型能有效解决这一问题。如图3(c)和图3(d)所示,在协同调度机制下,电解槽的功率调整更加频繁,以响应风电功率出力的波动性。在场景1下,系统的弃风率为12.7%;而在场景2下,由于电解铝企业参与协同调度,系统弃风率降低为3.5%,提高风电消纳量9.2%。

可以发现,电解槽在某些电价高的时段增加了用电量,这将导致企业的生产成本增加,如果不给予一定的利益补偿,电解铝企业经营者将不会参与协同调度。这也说明了引入纳什合作博弈利益分配模型的必要性,详细的数据分析将在4.2节中给出。

4.2 纳什合作博弈利益分配结果分析

在开展利益分配时,首先需要计算电网的总收益。在本文中,电网的总收益主要包括两个部分,即售电收益和新能源消纳补贴。图4展示了不同单位风电消纳补贴下的电网收益。电网经济收入随着单位风电消纳补贴的增加而增加。

图4 不同场景下电网收益情况Fig.4 Revenue of power grid under different scenarios

同时,本文主要采用清晰等价类处理源荷不确定性相关的模糊机会约束,置信度a的取值表征着电网控制中心对不确定性的包容度。为了量化置信度设置水平对系统风电消纳和收益的影响,本文选取单位风电消纳补贴为350元/MW,算例结果如图5所示。

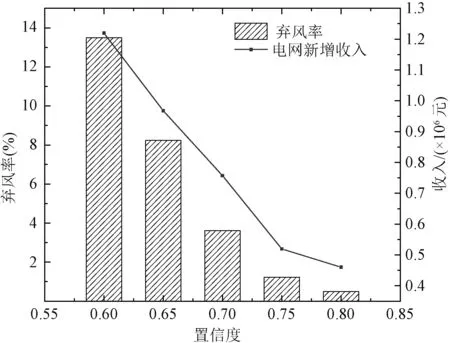
图5 置信度水平的影响分析Fig.5 Influence analysis of confidence level

观察图5可知,随着置信度水平的不断提高,电网的弃风率不断降低,但是电网的新增经济收入也随之降低,这是因为为了保证功率平衡和备用约束在此置信度水平下成立,电力系统需要预留更多的备用,这导致了电网收入的降低。这就对系统控制中心决策者提出了要求,决策者需要在弃风和电网经济收入间取得一定的平衡,实现经济效益和环境效益的最优。

最后,本文采用遗传算法求解纳什合作博弈利益分配模型式(17)、式(18)。各电解铝企业的议价能力指标dn取值为1.2和1.5。最终纳什合作博弈利益分配结果见表5。

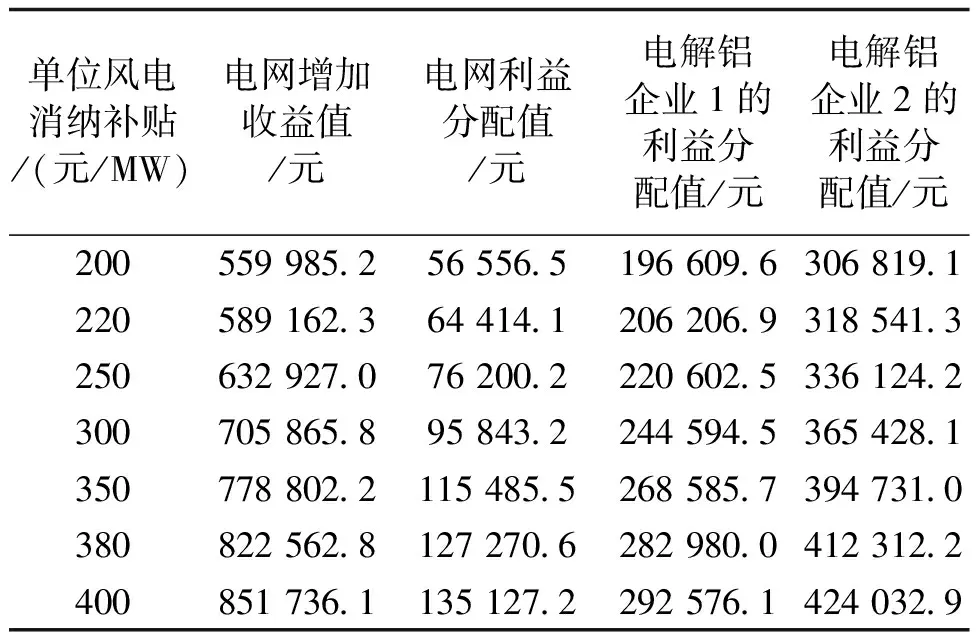
表5 纳什博弈利益分配结果Tab.5 Benefit distribution result of Nash game

由表5的纳什合作博弈利益分配结果可知,电解铝槽企业2的利益分配金额最大,这主要是由以下两点原因造成的:①相较于电网,电解铝企业通过增加在部分高电价时段的购电量,协助系统进行风电消纳,电解铝企业1增加运行成本127 531.4元,电解铝企业2增加运行成本222 446.8元,按照公平、公正的分配原则,电解铝企业2为新能源消纳和电网营收提高贡献最大,因此按照纳什合作博弈模型,电解铝企业2所得的补偿额度最大;②电解铝企业1和电解铝企业2的议价能力指标dn取值为1.2和1.5,则电解铝企业2的议价能力更强,所得利益更多。

同时需要说明的是,各电解铝企业在根据纳什合作博弈模型进行利益分配时,只需上报协同调度框架下的新增运行成本,不需要上报相关的产量信息和用电信息,有效地避免了商业隐私泄露现象的发生。

5 结论

电解铝企业用电量大,且往往建有自备电厂,具有显著的调度灵活性。通过算例分析,可以得到以下几点结论:

(1)通过发掘电解铝企业的调峰潜力,可以有效提高系统对新能源的消纳水平,降低系统弃风15%～20%。

(2)通过纳什合作博弈模型进行利益分配,能够在保证电解铝企业生产隐私的情况下,贯彻公平、公正合理的利益分配原则,保障参与协同调度各方的既得利益,实现多方共赢。

本文考虑的是静态分时电价下的高载能企业调度方式,随着我国电力市场机制的不断完善,节点电价正在逐渐普及,如何在节点电价下实现高载能最优调度的快速收敛是未来潜在的研究方向。同时,本文只考虑了单一类型的高载能企业的调度,未来可以考虑多类型高载能企业,如电解铝、钢铁冶炼、水电硅等,建立多类型负荷调度风险评估和利益分配模型。