谈“以生为本”自主探究学习课堂的建构
2023-07-28鲁彦
鲁彦
[摘 要] 数学学习是一个发展和完善的过程. 在实际教学中,教师应以生为出发点精心设计活动,让学生在观察、操作、探索、交流等活动中体验数学知识发现、发展和形成的过程,完成从感性认识到理性认识的过程,以此激发学生的潜能,发展学生的数学学习能力.
[关键词] 以生为本;自主探究;课堂建构
在教学中,教师应以生为出发点,以发展学生为目标,为学生提供参与课堂的机会,以此激发学生的学习兴趣,提升学生的学习技能. 笔者在教学“等腰三角形的性质”时,贯彻“以生为本”的教学理念,通过巧妙的活动设计让学生体验数学探究的魅力,让学生的学习兴趣得以激发,学习能力得以提升,现将教学过程整理成文,供大家参考.
教学分析
1. 教材分析
教学本课内容前,学生已经学习了三角形的概念及基础知识,具有“轴对称”学习的相关经验,这就为以“轴对称”为切入点开展自主探究活动提供了知识保障. 同时,本课内容又为学生后面要学习的判定定理提供依据,所以本节知识在本章知识中起着承上启下的作用. 此外,等腰三角形的底角相等、两腰相等、“三线合一”等性质在几何证明中有着重要的应用.
2. 教学目标
(1)理解并掌握等腰三角形的性质,能运用相关性质证明角相等的问题,能够独立完成一些简单的运算.
(2)通过观察、操作、交流等活动体验数学探究的乐趣,培养学生的观察、推理、抽象能力.
(3)通过“竞赛”等活动激发学生的探究欲,提高学生解决实际问题的能力.
3. 教学重、难点
(1)理解并掌握等腰三角形的性质.
(2)运用等腰三角形的性质解决简单的问题.
教学简录
1. 环节1:创设情境,复习导入
师:请同学们观看下面的图片,看看你能发现什么平面几何图形. (教师PPT播放图片:金字塔、斜拉桥、圣诞树等)
生(齐):等腰三角形.
师:很好,它就是今天我们课堂的主角.
师:请大家回忆一下我们学习了哪些与等腰三角形有关的知识.
设计意图借助生活图片让学生抽象出等腰三角形,点明本节知识探究的主題. 在此基础上,教师引导学生回忆等腰三角形的相关概念,如腰、顶角、底角等,为接下来的探究活动做铺垫.
2. 环节2:动手操作,探究新知
(1)剪一剪
师:你能在长方形卡纸上剪下一个等腰三角形吗?(教师让学生动手操作,很快学生就剪出了许多大小、形状不同的等腰三角形,接着教师让学生交流展示)
生1:利用等腰直角三角板可以画一个等腰直角三角形,然后剪下来就可以了.
生2:我是用折叠法操作的,先折一个正方形,然后沿着正方形的对角线剪开后就得到了2个等腰三角形.
生3:我是用尺规作图法先绘制了一个等腰三角形,再剪下来.
师:大家真厉害,想到了这么多办法. 我也有一个办法,先将这张长方形卡纸对折,然后在对折的纸上剪下一个三角形,展开后看看会得到什么三角形.(教师边说边操作)
学生齐声答:等腰三角形.
师:很好,我重复一下刚刚的过程,看看此时剪下的是什么三角形. (教师一边说一边演示)
生4:咦!为什么这次不是一个等腰三角形,而是两个普通的三角形呢?
师:对啊,这是为什么呢?
生5:第一次保留了折痕,是这样剪的;第二次没有保留折痕,是反过来剪的.(生5边说边演示,大家恍然大悟)
师:如果现在让你剪一个等腰三角形,你会怎么剪?
设计意图此环节,教师引导学生通过动手剪进一步强化他们对等腰三角形概念的理解. 在裁剪过程中,教师设计对折法裁切等腰三角形,进而以“轴对称”为切入点探究等腰三角形的性质. 此时,教师还引导学生对比上述操作,确定最优方案,培养学生的最优意识.
(2)想一想
师:你们觉得哪种方案更方便呢?
生(齐):老师的方案最方便.
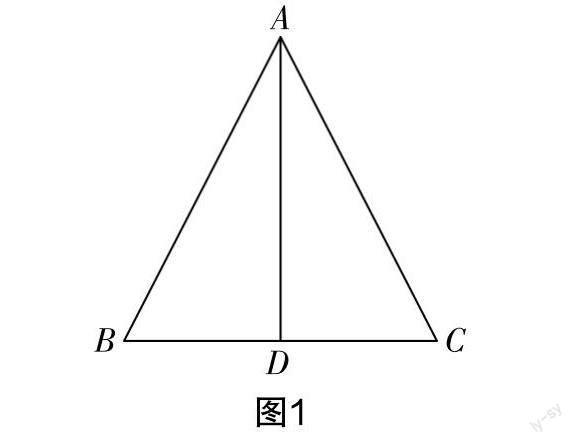
师:请大家按照这个方法剪一个等腰三角形,标上字母并描出折痕(如图1所示). (学生积极动手操作)
师:大家都剪好了吗?(学生点头表示已剪好)
师:观察自己裁剪下来的图形,思考等腰三角形是否为轴对称图形,并给出理由.
生6:等腰三角形是轴对称图形,它有一条对称轴,即折痕. 沿着折痕对折后左、右两边正好重合,符合轴对称的定义. (教师板书性质1:等腰三角形是轴对称图形)
设计意图让学生从做中抽象等腰三角形的性质,这既培养了学生的动手能力、观察能力,又锻炼了学生的数学抽象能力,促进了数学核心素养的落实. 同时,学生通过亲身经历感受到了学习数学的乐趣,激发了探究兴趣,促进了知识的深化和能力的提升.
(3)找一找
师:结合图1找一找,除了AB=AC,是否还存在相等的线段或相等的角. (教师启发学生运用性质1寻找图中的相等关系)
生7:BD=CD,∠B=∠C,∠ADB=∠ADC,∠BAD=∠CAD.
师:很棒,其他人还有补充吗?(学生摇头表示没有补充)
师:∠B,∠C是等腰三角形的什么角?
生(齐):底角.
师:很好,这样我们就得到了等腰三角形的什么性质?
生8:等腰三角形的两个底角相等. (教师板书性质2)
师:由∠BAD=∠CAD,你们有什么发现?
生9:AD是顶角∠BAC的平分线.
师:由∠ADB=∠ADC=90°,我们又知道了什么?
生10:AD是底边BC上的高.
师:那由BD=CD又能知道什么呢?
生11:AD是底边BC的中线.
师:这个AD真不简单,它既是顶角的平分线,又是底边上的中线和高. (教师板书性质3:“三线合一”)
为了强化学生对“三线合一”的理解,教师设计了一些针对性的练习,如给出等腰三角形底边上的中线,让学生寻找相等的角、相等的边、垂直关系等,以此促进学生对知识的深化理解.
设计意图教师引导学生寻找等腰三角形中的等量关系,并通过逐层引导让学生发现等腰三角形的“三线合一”性质. 这样便让学生经历了知识的发现和形成过程,有利于学生知识的深化和兴趣的激发.
(4)比一比
师:在三角形中是否存在第二条“AD”?(教师鼓励学生合作探究)
问题给出后各小组积极动手实验,此时学生先以∠ABC为例,画出了∠ABC的平分线、AC边上的高和AC边上的中线,但他们发现这三条线并不重合. 同理,∠ACB的平分线、AB边上的高和AB边上的中线也不重合. 于是学生明晰“三线”是等腰三角形底边上的高、底边上的中线及顶角平分线.
设计意图通过“比一比”,学生明晰了“三线”具体指哪“三线”,从而深化了对“三线合一”的理解.
此环节,教师通过逐层导入带领学生经历了发现三角形性质的过程,整个过程轻松愉悦,学生收获满满,提升了课堂教学的有效性.
3. 环节3:自主探索,解决问题
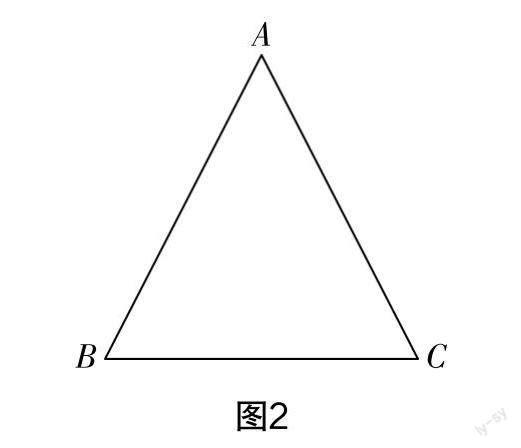
问题1:如图2所示,△ABC是等边三角形,它的三个内角有什么关系?你能求出每个内角的度数吗?
(教师让学生独立思考,板演证明过程,并进行总结归纳,即等边三角形的三个内角都相等,都等于60°)
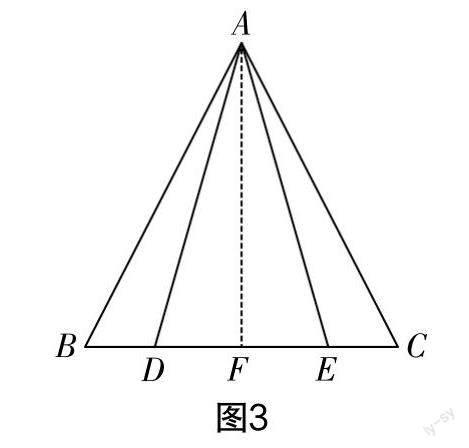
问题2:如图3所示,在△ABC中,AB=AC,D,E两点在边BC上,且AD=AE,求证:BD=CE.
问题2略有难度,教师鼓励学生互动交流. 在教师的啟发和引导下,学生逐渐完善了证明过程,并知晓了什么叫辅助线及辅助线的画法.
设计意图借助具体问题强化学生对等腰三角形性质的理解,能培养学生的数学应用意识. 此环节教师鼓励学生独立思考和合作交流,让学生的思维能力在思考、探索和交流中得到发展与提升.
4. 环节4:灵活应用,巩固新知
在此环节,教师精心设计练习,并采取“竞争”的方式点燃了学生参与课堂的热情. 通过练习,学生巩固了知识,在成功的喜悦中增强了学习信心,激发了学习兴趣.
5. 环节5:小结反思,知情共融
在此环节,教师预留时间让学生总结归纳,提出自己的所思、所想、所获,进而通过有效的反思、交流逐渐升华认知,实现知识内化. 有效的反思归纳能让学生感受到数学学习是一件有趣且有意义的事,从而树立正确的学习观和价值观.
教学思考
本课教学以学生的已有认知为起点,通过环环相扣的问题引导学生动手做、动口说、动脑思,充分地调动了学生参与课堂的积极性,并让学生的观察能力、操作能力、数学抽象概括能力得到了稳步提升. 例如,在教学中,学生通过“剪一剪”“想一想”“找一找”“比一比”等活动得到了等腰三角形的性质,经历了“三线合一”性质形成和验证的过程,并借助积极有效的互动激发了学习热情,于潜移默化中提升了学习能力.
总之,在教学中,教学设计应以发展学生为目标,应遵循学生的认知发展规律,应让学生在观察、探索、交流中经历知识的形成与发展过程,以此实现知识的巩固与深化,促进学生学习能力的提升.
