“双减”背景下初中数学作业“三化一体”设计模式的研究

［摘  要］ “双减”政策要求减轻义务教育阶段学生过重作业负担和校外培训负担. 在校内，“双减”政策有效落地的关键是“双提”，即提升课堂质量，提高作业质量. 当前初中数学作业设计存在的问题有“二量”难并举，功能太单一，结构不合理，差异难协调，时间难统一. 基于以上作业设计现状及初中数学学科的特点，文章提出，可将作业设计融入课初、课中、课后，采用 “三化一体”的作业模式来优化习题数量，提高作业质量.

［关键词］ 双减；初中数学作业；三化一体

作者简介：王进（1982—），本科学历，中学一级教师，广州市花都区初中数学教研员，“新世纪初中数学杰出教师”第四期成员，广东省骨干教师，曾获得第二届“新世纪杯”全国初中数学优质课一等奖、第七届“卡西欧杯”全国初中数学优质课一等奖等荣誉.

当前初中数学作业设计存在的问题

1. “二量”难并举

“二量”难并举，也就是作业数量减少，作业质量未提升. 目前，初中阶段数学作业的数量减少了，但作业设计质量还停留在原水平，所以部分学生的学习质量有所下降.

2. 功能太单一

大部分教师认为作业主要是巩固课堂所学的知识，可见这些教师缺乏目标意识，作业目标指向单一，且低水平目标较多.

3. 结构不合理

目前，很多教师布置的作业，目标、难度、类型等分布比例不合适，设计缺乏整体性、序列性. 且作业以书面作业为主，类型单一，机械重复性作业过多［1］.

4. 差异难协调

目前，针对不同学生的差异性布置的作业不多. 低难度和中等难度的作业过多，而难度大的作业又不符合学生的身心特点，或远超课标要求.

5. 时间难统一

很多教师很难把控学生完成作业的时长，一是学生差异大，二是难以把控学生思考难题的时间.

“三化一体”作业设计模式内容概述

基于以上作业设计现状及初中数学的学科特点，笔者经过一年的设想和小范围的实践，认为可将作业设计融入教学设计，把作业设计分为课初、课中、课后三部分，通过一体化设计来优化习题数量，提高作业质量，也就是初中数学作业设计采用“三化一体”的模式.

1. “三化”是什么

（1）课初：旧知反馈“同步化”

在课初设置“3分钟作业”，作业均来源于上节课所学内容、本节课所需旧知，这样能达到“微检测”的目的，且教师可依据学生的完成情況来引入新课. 可见，“3分钟作业”与“微检测”、教学设计引入进行了有机结合，使得作业具有两大功能，即①诊断功能：以“微检测”的形式反馈学生掌握旧知的情况；②辅助功能：数学知识之间具有关联性，教师可用旧知引出新知.

（2）课中：随堂作业“规范化”

将课堂中的随堂练习当成作业来设计，侧重体现作业的两大功能，即①固知功能：围绕数学教学目标，有计划、有步骤地设计课堂作业，让随堂作业遵循适量性、典型性、层次性的原则，从而达到巩固新知的目的；②育人功能：课堂作业最大的优势是教师可现场指导学生完成，此时教师可在解题的规范、严谨、美化等方面做要求，进而培养学生数学解题的规范性、严谨性.

（3）课后：难题思维“可视化”

一般地，教师难以把握学生解决数学课后作业难题的情况，因为解题时间难把握，解决程度难把握. 针对这些问题，笔者认为可以采用“思维导图”的方式，即让学生画出解题的思维导图，通过思维导图呈现学生的思维过程，将隐性思维可视化. 思维导图作业具有两大功能，即①指导功能：思维导图能让学生完成作业后认识到解答该类数学问题的思维与方法；②分层功能：针对综合题，优生可独立完成，其余学生可通过参考“解题思维导图”来完成，进而达到作业分层的目的. 此外，教师还可以通过布置学生绘制难题“思维导图”的作业来发展学生的高阶思维.

2. “一体”是什么

将课初、课中、课后教学环节的习题当成作业设计的一部分通盘考虑，通过“一体化”设计，明确各部分作业的功能，进而优化作业数量，体现作业功能.

笔者经过实践，论证了初中数学作业设计“三化一体”模式的有效性. 该模式除了能体现作业的六大功能，还能提升教师的作业设计水平，提高初中数学作业设计的质量，最终达到初中数学教学“轻负高质”的目的，有效落实“双减”政策. “三化一体”模式的图示如图1所示.

特色与创新之处

1. 作业“一体化”设计

将课初、课中、课后教学环节的习题当成作业设计的一部分通盘考虑，将数学作业设计与教学设计有机结合，通过“一体化”设计，明确各部分作业的功能，进而优化作业数量［2］.

2. 多维度、多角度、多程度体现作业功能

在作业设计的三个时段实行“三化”：课初，旧知反馈“同步化”；课中，随堂作业“规范化”；课后，难题思维“可视化”.

体现作业的六大功能：诊断功能，辅助功能，固知功能，育人功能，指导功能，分层功能.

3. 数学作业难题“思维可视化”是“三化一体”模式最大的创新

用“思维导图”来呈现思维形成过程，将隐性思维可视化，体现了作业的指导功能和分层功能. 特别地，分层功能是通过同一题目对学生的不同要求来体现的.

4. 在作业设计中实施“闭环式”管理

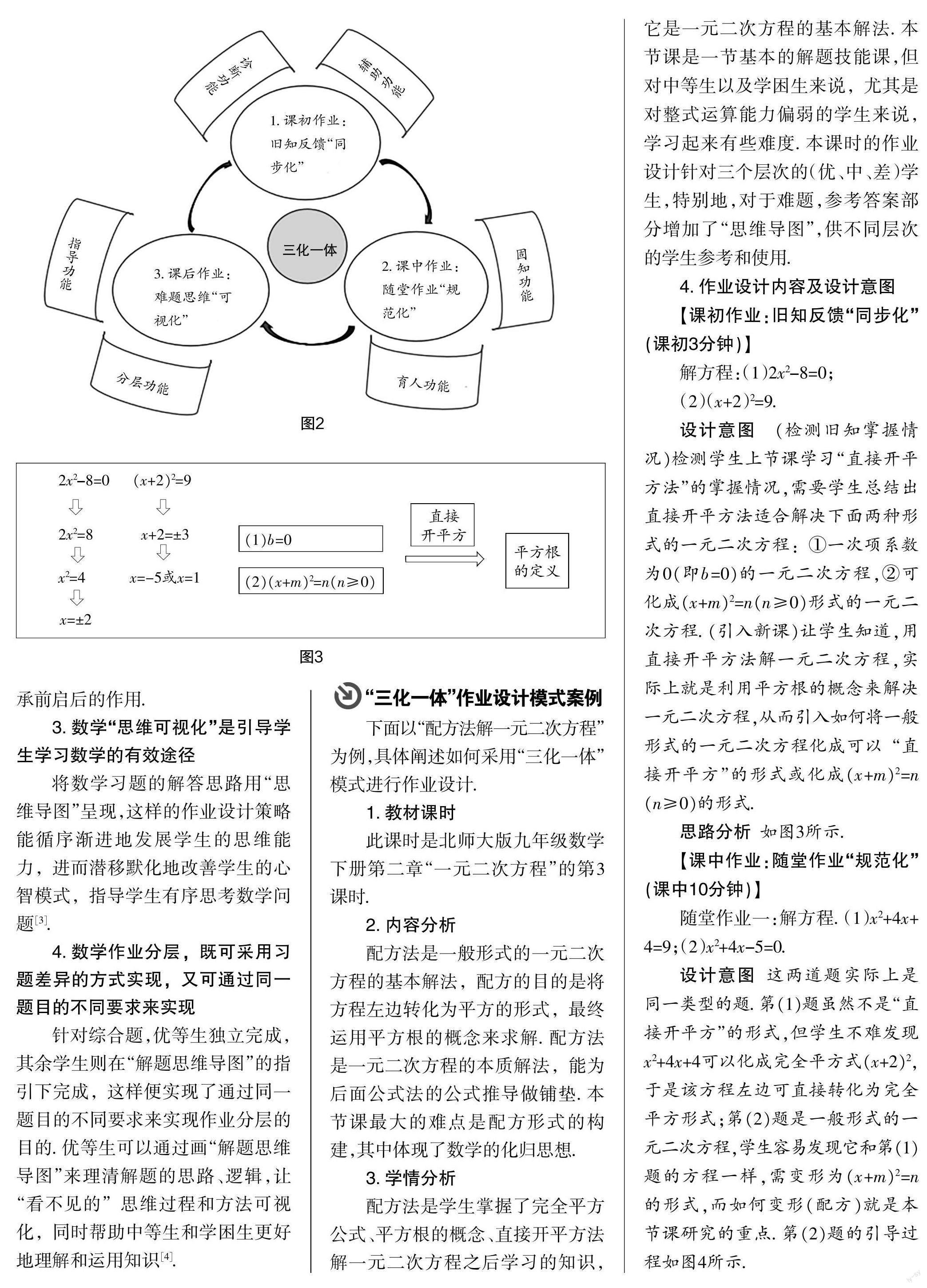
课后学生的作业完成得不理想的地方，可以作为下一课时课初作业设计的素材，这样闭环式的设计，能达到知识有效落实的目的. “三化一体”模式闭环式管理图示如图2所示.

主要观点

对于“三化一体”模式，有以下四个观点.

1. 将数学作业设计融入数学课堂设计之中

初中生每天的数学学习时间约60分钟（上课40分钟，课后20分钟），教师可将教学各环节的习题进行“一体化”设计：课初作业3分钟左右，课中作业8分钟左右，课后作业20分钟左右. 这样统筹考虑，不仅能优化习题质量，让各部分作业有针对性，还能最大限度地体现作业的各个功能.

2. 作业既可以具有检测功能，又可以引入新课

课初作业可作为“微检测”，将以往单元测试碎片化的知识同步呈现，同时考虑新、旧知识间的内在联系，将课初作业融入课堂设计，起到承前启后的作用.

3. 数学“思维可视化”是引导学生学习数学的有效途径

将数学习题的解答思路用“思维导图”呈现，这样的作业设计策略能循序渐进地发展学生的思维能力，进而潜移默化地改善学生的心智模式，指导学生有序思考数学问题［3］.

4. 数学作业分层，既可采用习题差异的方式实现，又可通过同一题目的不同要求来实现

针对综合题，优等生独立完成，其余学生则在“解题思维导图”的指引下完成，这样便实现了通过同一题目的不同要求来实现作业分层的目的. 优等生可以通过画“解题思维导图”来理清解题的思路、逻辑，让“看不见的”思维过程和方法可视化，同时帮助中等生和学困生更好地理解和运用知识［4］.

“三化一体”作业设计模式案例

下面以“配方法解一元二次方程”为例，具体阐述如何采用“三化一体”模式进行作业设计.

1. 教材课时

此课时是北师大版九年级数学下册第二章“一元二次方程”的第3课时.

2. 内容分析

配方法是一般形式的一元二次方程的基本解法，配方的目的是将方程左边转化为平方的形式，最终运用平方根的概念来求解. 配方法是一元二次方程的本质解法，能为后面公式法的公式推导做铺垫. 本节课最大的难点是配方形式的构建，其中体现了数学的化归思想.

3. 学情分析

配方法是学生掌握了完全平方公式、平方根的概念、直接开平方法解一元二次方程之后学习的知识，它是一元二次方程的基本解法. 本节课是一节基本的解题技能课，但对中等生以及学困生来说，尤其是对整式运算能力偏弱的学生来说，学习起来有些难度. 本课时的作业设计针对三个层次的（优、中、差）学生，特别地，对于难题，参考答案部分增加了“思维导图”，供不同层次的学生参考和使用.

4. 作业设计内容及设计意图

【课初作业：旧知反馈“同步化”（课初3分钟）】

解方程：（1）2x2-8=0；

（2）（x+2）2=9.

设计意图  （检测旧知掌握情况）检测学生上节课学习“直接开平方法”的掌握情况，需要学生总结出直接开平方法适合解决下面两种形式的一元二次方程：①一次项系数为0（即b=0）的一元二次方程，②可化成（x+m）2=n（n≥0）形式的一元二次方程. （引入新课）让学生知道，用直接开平方法解一元二次方程，实际上就是利用平方根的概念来解决一元二次方程，从而引入如何将一般形式的一元二次方程化成可以“直接开平方”的形式或化成（x+m）2=n（n≥0）的形式.

思路分析如图3所示.

【课中作业：随堂作业“规范化”（课中10分钟）】

随堂作业一：解方程. （1）x2+4x+4=9；（2）x2+4x-5=0.

設计意图这两道题实际上是同一类型的题. 第（1）题虽然不是“直接开平方”的形式，但学生不难发现x2+4x+4可以化成完全平方式（x+2）2，于是该方程左边可直接转化为完全平方形式；第（2）题是一般形式的一元二次方程，学生容易发现它和第（1）题的方程一样，需变形为（x+m）2=n的形式，而如何变形（配方）就是本节课研究的重点. 第（2）题的引导过程如图4所示.

[x2+4x+4=9][图4][x2+4x=5][（x+2）2=9][x2+4x-5=0][配方][显性

呈现]

随堂作业二：解方程 . （1）x2-4+6x=9；（2）x（x-3）+1=0.

设计意图让学生通过解答以上习题明确运用配方法解一元二次方程的基本思路：“化”（化成二次项系数为1的一般形式）——“移”（移项，呈现显性的易配方的式子）——“配”（配成完全平方式，呈现直接开平方的形式）——“开”（开方，利用平方根的概念）；让学生理解运用配方法解一元二次方程的算理，规范学生的解题步骤. 运用配方法解一元二次方程的基本思路如图5所示.

[图5][化 ? 移 ? 配 ? 开]

【课后作业：难题“思维可视化”（课后20～25分钟）】

课后作业采用“2+1+1”的模式，即2道基础必会题、1道变式中层题、1道综合较难题.

课后作业一：2道基础必会题.

（1）配方：x2-12x+___=（x-___）2；x2+5x+___=（x+___）2；a2___+5=（a-___ ）2.

（2）解下列方程：① x2-6x+5=0；②x2-1=4x；③x（x-5）-1=0.

设计意图基础必会题，是通过本节课的学习，所有学生必须会做的题，属于知识掌握的最低要求. 以上作业能达到巩固基础、规范答题、反馈情况的目的.

课后作业二：1道变式中层题.

解关于x的方程：x2+2x+q=0（其中q≤1）.

设计意图本题为中层题，难在多了一个参数q. 此题能强化学生运用配方法解一元二次方程的能力，也能为后面学习公式法解一元二次方程中的公式推导做铺垫.

课后作业三：1道综合较难题.

阅读材料：把形如ax2+bx+c（a≠0）的二次三项式（或其一部分）配成完全平方形式的方法叫配方法. 配方法的基本形式是完全平方公式的逆写，即a2±2ab+b2=（a±b）2. 例如，（x-1）2+3，（x-2）2+2x，

x-22+x2是x2-2x+4的三种不同形式的配方（即“余项”分别是常数项、一次项、二次项）.

请根据阅读材料解决下列问题：

（1）参照上面的例子，写出x2-4x+2三种不同形式的配方；

（2）已知a2+b2+c2-ab-3b-2c+4=0，求a+b+c的值.

设计意图本题是一题综合性较强的试题，难度偏大，教师教学时可以用“思维导图”来呈现思维形成过程，让学生理解到：二次三项式配方的本质是“以其中两项为准，拆第三项”，教材呈现的配方法只是其中一种. 本题第（1）问是模仿例题进行三类配方，第（2）问是通过式子的特点，选择合适的配方形式，将二次七项式配成三个完全平方式. 优等生可独立完成，中等生及学困生可通过参考优等生的“解题思维导图”完成此题的解答，这能达到控制作业时间的目的. 此题的“思维可视化”内容如图6所示. 特别地，图6可放在参考答案的开头.

上述“配方法解一元二次方程”的作业设计能循序渐进地发展学生的思维能力，能指导学生有序地思考数学问题［4］.

参考文献：

［1］王月芬. 透析作业——基于30000份数据的研究［M］. 上海：华东师范大学出版社，2014.

［2］王月芬. 作业设计能力——未被重视的质量提升途径［J］. 人民教育，2018（z2）：58-62.

［3］加德纳. 智能的结构［M］. 沈致隆，译. 北京：中国人民大学出版社，2008.

［4］刘濯源. 初中思维导图高效学习模板［M］. 沈阳：辽宁人民出版社，2010.