特殊化原则的理论探析与教学思考
2023-07-27李亚琼徐文彬宁连华
李亚琼 徐文彬 宁连华


【摘 要】 特殊化原则是将问题转化为特殊情形,通过对特殊进行分析去寻求一般,以获得关于所研究对象的性质或关系,从而找到解决问题的方向、途径或方法的思维方式.特殊化原则的使用过程蕴含化归思想、“以退求进”等策略,具体表现有:概念特殊化、解决问题特殊化或命题特殊化等.特殊化原则的思维具有多元性与多向性、程度性与抽象性、条件性及解释性等特性.特殊化原则是数学学习中的重要思维方式,结合特殊化原则的理论思考,从“几何”“函数”“数与式”及“锐角三角函数”4个知识主线思考教学落实.
【关键词】 特殊化原则;维维亚尼定理;多元性与多向性;条件性与解释性
《义务教育数学课程标准(2022年版)》中强调,数学学习中,要重视数学结果的形成过程,注重引导学生在真实情境中发现问题和提出问题,利用猜测、推理、想象等方法分析问题和解决问题,从而促进学生体会和运用数学思想方法 [1] .这里的猜测、推理、想象等蕴含由特殊看一般的思维方法,数学学习时可以先看特殊情况,然后从特殊情况的结果推广到一般情况,这样的学习过程蕴含“特殊化”的思维方法.
1 问题的提出(“一段三角关系”)
引例 假设一个任意正三角形(如图1所示),对于三角形内任意一点P,考虑它和三边的垂直距离x,y,z.对于距离和x+y+z,可以得出什么结论? [2] 图1 三角形内一点 图11 P点在三角形____与三边的距离_____的顶点
为了猜想一般结论,不妨可以先研究一些特例.比如,将P点移至三角形的某个顶点(如图11),于是P点和两边的距離为0,此时与对边的距离就变成三角形的高h.由此,就可以作出猜想:距离和x+y+z=h.将P点移至三角形的某个顶点,这是一种相当大的“让步”,以退求进式的探索,目的是给猜想提供方向.
下面继续推进,思考稍微一般性的特例,不妨可以让P点移至三角形的其中一条边上.由图12易知,△ABP≌△PCA(三个角均对应相等,斜边重合),于是可得y+z=h,因为x=0,所以x+y+z=h.图12 P点在三角 图13 P点在三角形 形的边上______ 的任意位置
由此继续推进研究进程,事实上,P点在三角形内的任何位置,均可以借鉴以上特殊情况,于是作出如图13的处理:过P点作线段DE与AB平行,分别交边AC和BC于点D和E,则△CDE也是正三角形.于是由上面的特例可知,y+z=h*,又易知,h=h*+x,因此可得,x+y+z=h,这样便验证了猜想并得出了一般情形的结论.这便是维维亚尼定理的基础几何定理,是以意大利数学家维维亚尼(Vincenzo Viviani,1622—1703)来命名的 [2]129 .这个定理有个漂亮的应用:x+y+z=常数的三个量的连比x∶y∶z,可以用三角形里的一点来表示,这便是三线坐标.
引例先验证合适的特例,再尝试使用已经证明的特殊情况解释一般情况或者更多的特例,然后再从特殊情况推到一般情况,这便蕴含特殊到一般的思维方法.用特殊研究一般的数学思维方法经常运用于数学教学和解题中,称之为“特殊化原则”,本文将研究该思维方法的理论机制,并结合理论探索思考如何具体运用于教学实践.
2 “特殊化原则”的思维结构
首先来分析特殊化的涵义,基于此再来探索特殊化原则的表现形式和思维特性.
2.1 特殊化的涵义
特殊化是把研究对象或问题从原有的范围缩小到较小范围或个别情况进行考查的思维方法.由于一般性总是寓于特殊性之中,所以要研究某一对象或问题时,就可以先考察它的若干个特殊情况,利用各个特殊情况中包含的共性与个性,通过比较与归纳、分析与综合来把握原有对象或问题的有关性质 [3] .引例中便运用特殊情形(分别将P点移至三角形的某个顶点,P点移至三角形的其中一条边上,继而P点在三角形内的任何位置)对结论进行猜想,然后一步步推进到更一般的情形.在思考一般情形时,又再次借鉴特殊情形的思考策略去考虑,由此验证出一般情形时结论的成立.特殊化原则是视原问题为一般,构造特殊问题,通过对特殊问题的探究而获得原问题的解决,其中把特殊化作为转化的策略.所以,特殊化原则蕴含化归思想,是将问题化归为特殊情形 [4] ,然后在特殊情形基础上解决一般情形问题的方法.
2.2 特殊化原则的思维特性
特殊化原则中蕴含“退”的策略,即“以退求进”的思维方法.所谓“退”就是从复杂退到简单,从一般退到特殊,从抽象退到具体,从一般条件(位置)退到特殊条件(位置)等.比如,引例中,便是先退到“P点移至三角形的某个顶点”“P点移至三角形的其中一条边上”,继而找到对一般结论的猜想方向(x+y+z=h).同时对一般情形(P点在三角形内的任何位置)的思考时,又通过构建类似特殊情形(P点移至另一个正三角形的其中一条边上)继续借鉴思考,可以看出特殊中蕴含一般,同时一般中又渗透对特殊的借鉴.
正如华罗庚先生所说,退到最原始而又不失去重要的信息,把特殊的弄清楚,获得解题思路或者解题方向,从而猜想一般问题的结论,然后再“进”到一般性问题上来,具体表现有:极端值原则、特例、反例等 [5] .当然,在研究问题时可以将研究问题或对象看成一般性问题或对象,按照增加约束条件,取其局部或个别情形进行考查等方式得出.通过对特殊和个别的分析去寻求一般,以获得关于所研究对象的性质或关系等认识,找到解决问题的方向、途径或方法.
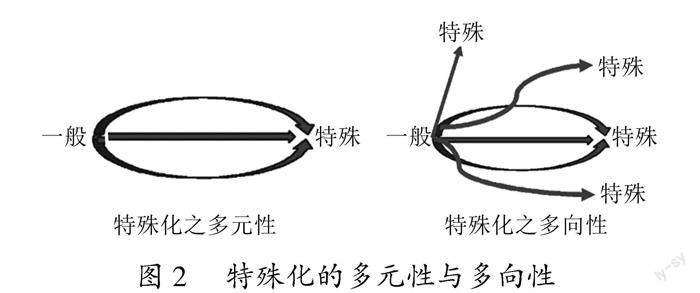
对于一个知识的认识,总是由表及里、由定量到定性.对特殊化原则的思维特性的探析也需要这样的过程.(1)多元性和多向性.从一般对象过渡到特殊对象的具体实现途径有很多种,这就体现特殊化原则的多向性和多元性.多向性是指可以沿着不同的方向进行特殊化,多元性蕴含殊途同归性,多元性是多向性的一种特殊表现(具体见图2).(2)程度性和抽象性.特殊化原则的多元性和多向性就决定了特殊化原则的程度性,在数学探究中运用特殊化原则,体现数学抽象的过程.(3)条件性及解释性.一个数学对象能否实现某种特殊化,是与某些条件是否具备相关的,所以特殊化原则使用时具有条件性,比如引例中是在正三角形这样的背景下进行的;特殊情形的结论可以解释或猜测一般情形的结论,而对一般情形结论的思考可以借鉴特殊情形结论的探究方法或策略,因此特殊性原则具有借鉴性和解释性(具体见图3),对知识的特殊化、具体化就是对事物的一种理解,体现化归与转化.
2.3 特殊化原则的表现形式
“一般到特殊”及“特殊到一般”是学生学习知识两个相互联结的环节.学习活动中,这两个环节总是循环互生的,即学生首先需要认识某知识的特殊本质,才能更进一步认识知识的一般本质.当学生认识了某知识一般属性后,才能以此为基础认识指导自己继续认识新的知识,继而使得认识过程不断深化.数学概念在数学知识及理论体系中处于基础的地位,所以特殊化的具体表现形式首先是“概念形成的特殊化”.数学学习的过程是不断提出问题、解决问题的过程,于是特殊化的另一表现形式为“解决问题的特殊化” [5]94 .当问题解决后,其结果在数学理论体系中以命题形式出现,所以特殊化的第三种表现形式为“命题的特殊化”.
(1)特殊化渗透概念教学
数学对象往往是由某些性质规定或刻画的实体,对数学对象的变换可从性质和实体两个方面的变换来进行,特殊化也是这样进行的,特殊化渗透概念教学时蕴含“现象—表象—抽象”的过程.数学学科的特殊性蕴含数学知识表征的特殊性,其中严谨性、抽象性、符号化、结构化等是数学的典型特征,这导致数学概念、命题的教学需要动态建构.因数学概念表现形式具有多样性,所以在教学中,学生需要充分直观感受数学认知对象,才能逐渐抽象出知识的本质特征,继而规范出知识概念,充分直观感受的过程便蕴含特殊化,抽象出一般知识表征的过程便蕴含由特殊到一般和归纳,再将所学的知识运用的过程,又体现一般到特殊和演绎.所以特殊化原则在概念课教学中的运用总伴随“特殊到一般”“一般到特殊”的循环互生.
(2)解决数学问题的特殊化
在解决问题时,特殊化也是特别有用的方法,主要表现为:特殊点、特殊位置、特殊值等.问题特殊化在求定值、定点问题时经常适用,比如求y=a(x-2)+3所过的定点,由于a的任意性,所以直接令x-2=0,于是得出定点为(2,3),这样的处理过程体现问题的特殊化.
当然,有时解决一个问题时,并不需要问题本身的特殊化,只需考虑问题的某些特殊方面,即考虑其某些特殊的构成对象或某些特殊的关系.利用特殊化原则解题时,对个别特殊情况的讨论,往往蕴含解决问题的关键策略,可以提示问题的解决方向 [6] .可以从特殊化问题求解的关键性步骤中找到解决一般性问题的方向或突破口,寻求到有益的启示,从而发现一般化问题的解题关键.
(3)命题的特殊化
命题特殊化是数学知识的呈现方式之一,数学定理的推论便是命题的特殊化.比如命题“直径所对的圆周角是直角”便是“同弧所对的圆周角是圆心角的一半”的特殊情况.命题的特殊化实质体现对命题的解释性,从逻辑意义上看,一个命题的结论特殊化的情形越多,则该命题包含的信息越多,于是该命题越具有一般性.波利亚说过,强化条件或减弱结论是对命题特殊化变换的两个基本手段 [5]97 .
2.4 特殊化原则在培养学生数学思维中的价值
特殊化原则是数学学习中的重要思维方式,运用特殊化原则有利于培养学生的直觉思维、合情推理能力、探索与创新能力等.直觉思维是数学思维的基本形式之一,直觉思维以学生已有知识及经验为基础,对研究的问题提出合理的猜测和假设,过程中蕴含顿悟与发现.特殊化原则侧重于运用特殊化的策略,挖掘问题中隐含的特殊条件和内在联系,这样的过程可以培养学生的直觉思维,思维过程蕴含非逻辑性和突发性 [7] .特殊化原则侧重宏观上的探索,暂时忽略逻辑严谨性,重在发现关系找出规律,其表现为结合一定的数学依据进行探索的过程,而这便是合情推理的思维特点.当然特殊化原则的使用中,既需要合情推理也需要逻辑推理,以得到更一般结论的严格说明.此外,特殊化原则在探索思路、发现问题中起到导引作用,其体现数学学习过程的发现性.教学过程中渗透特殊化原则可以培养学生的探索精神和创造力.
3 特殊化原则的教学思考
基于以上对特殊化原则的理论剖析,教师需要在教学中尝试渗透特殊化策略,以达到对学生思维能力的培养.初中数学教学中,需要结合特殊化原则的理论思考,贯穿于知识教学中,下面主要从“几何”“函数”“数与式”“锐角三角函数”4个知识主线去思考教学落实.
3.1 几何中的运用
圆的知识学习中,学生在灵活运用上较为困难.究其原因,就是圆的性质和要素较多,有时还需要借助辅助线去优化解题.而在解决圆的相关问题时,特殊化原则会起到很重要的作用,比如下面的例子中,便很好地渗透了特殊化原则的运用过程,同时也优化了解题思路.
例1 (1)如图4,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D, AE = AB ,BE分别交AD,AC于点F,G.判断△FAG的形状,并说明理由.(2)如图5,若(1)中的条件变为“点E与点A在直径BC的两侧,BE,AC的延长线交于点G,AD的延长线交BE于点F”,其余条件不变,判断△FAG的形状,并说明理由.
分析 结论:△FAG均为等腰三角形.第(1)题是较为特殊的情形,即点A和点E在直径BC的同侧,此时较为容易判断△FAG的形状.随后,在说明“点E与点A在直径BC的两侧”时,可以类比同侧的特殊情形证明更一般情形.具体说明如下:
(1)如图4,因为BC是⊙O的直径,所以∠BAC= 90 °(直徑所对的圆周角是直角),
所以∠ABE+∠AGB= 90 °.因为AD⊥BC,所以∠DAC+∠ACB= 90 °.
又因为 AE = AB ,所以∠ABE=∠ACB(等弧所对的圆周角相等),
所以∠AGB=∠DAC,所以△FAG为等腰三角形.
(2)如图5,因为BC是⊙O的直径,所以∠BAC= 90 °(直径所对的圆周角是直角).
所以∠ABG+∠AGB= 90 °.因为AD⊥BC,所以∠DAC+∠ACD= 90 °.
又因为 AE = AB ,所以∠ABG=∠ACB(等弧所对的圆周角相等)
所以∠AGB=∠DAC.即∠AGF=∠FAG.所以△FAG为等腰三角形.
在以上证明过程中,便利用当问题条件由特殊变一般,结论不变.此时可以借鉴特殊条件时的证明思路(“同余”),对一般情形的结论加以证明.教学中,使用特殊化原则蕴含思维的抽象性、解释性和借鉴性的特点.
3.2 函数中的运用
初中数学教学中,特殊化原则也经常渗透于函数(一次函数、二次函数或反比例函数)知识教学中.
例2 (2014玄武一模)在平面直角坐标系中,O为坐标原点,一次函数y=ax+b图象与二次函数y=ax2+bx的图象交于点A,B.其中,a,b均为非零实数.
(1)当a=b=1时,求AB的长;
(2)当a>0时,请用含a,b的代数式表示△AOB的面积;
(3)当点A的横坐标小于点B的横坐标时,过点B作x轴的垂线,垂足为B′.若二次函数y=ax2+bx的图象的顶点在反比例函数y=ax的图象上,请用含a的代数式表示△ABB′的面积.
分析 对第(1)问的思考,主要基于a=b=1特殊情况出发,将函数表达式联立得方程组,求得方程组的解,所对应的即为两个函数图象的交点坐标,利用勾股定理将点坐标转化为线段的长度,从而解决问题.第(2)问,将情况推广到一般,即当a>0,b为任意时,学生需要由具体(特殊)思考抽象(一般),计算出A(-ba,0),B(1,a+b),借助分类讨论(b>0;-a
3.3 数与式中的运用
数与式部分经常会出现找规律题型,这些题的思考中,需要教师引导学生从特殊情形中归纳出一般情形的结论,并验证.这样的知识载体与特殊化原则的融合运用,也蕴含培养学生对知识的迁移能力.
例3 观察下列等式:x1=1+112+122=1+11×2,x2=1+122+132=1+12×3,
x3=1+132+142=1+13×4,……
(1)根据以上规律归纳出:
①x5==;
②xn==.
(2)请证明(1)中②这个等式.
分析 特殊化原则在数与式中的运用,一般会以找规律的样态出现,比如,例3中根据已知的条件,续写x5=1+152+162=1+15×6,由特殊情形的几个例子猜测更一般的情形xn=1+1n2+1(n+1)2=1+1n×(n+1),这样的过程需要学生的归纳能力和类比能力.验证xn表达式成立的过程,考查学生对知识的迁移能力,灵活运用数与式运算技巧,才能实现从特殊到一般的“突破”.
(验证过程:左边=xn=n4+2n3+3n2+2n+1n2(n+1)2=(n4+2n3+n2)+(2n2+2n+1)n2 (n+1) 2=n2 (n+1) 2+2n(n+1)+1n2 (n+1) 2=[n(n+1)+1]2n2 (n+1) 2=n(n+1)+1n(n+1)=1+1n(n+1)=右边,所以结论得证!)
3.4 锐角三角函数中的运用
特殊化原则的运用,需要以真实情境为背景,以具体知识为载体,选择有针对性的对解题有意义的特殊情况,强调知识和策略方法的迁移性,比如在锐角三角函数的教学中也有体现.
例4 (2015玄武一模)在某两个时刻,太阳光线与地面的夹角分别为37°和45°,树AB的高为6m.
(1)如图6,若树与地面l的夹角为90°,求两次影长的和CD;
(2)如图7,若树与地面l的夹角为α,求两次影长的和CD(用含α的式子表示).
(参考数据:sin 37 °≈0.60,cos 37 °≈0.80,tan 37 °≈0.75.)
分析 第(1)问从特殊的状态出发,因为“树与地面l的夹角为90°”,所以直接运用锐角三角函数解决问题,分别在两个直角三角形中已知一边一角,解出直角三角形的CB和BD,从而求解.第(2)问可以借鉴第(1)问(特殊情况),因为“树与地面l的夹角为α”,此处α不一定为90°,所以构造直角三角形,即过点A作AH⊥CD(如图8所示),得到三个直角三角形,其中AH为公共边. 图8在直角三角形ABH中已知一边一角,可以表示AH,转化为(1)的问题便可以求解.
总之,特殊化原则蕴含特殊化与一般化的融合,基于特殊研究一般,再利用一般应用于特殊,特殊是基础与引领,一般是深化与目的.数学教学中,教师需要引导学生运用特殊化原则分析抽象难懂的数学问题,让学生养成运用特殊化原则辅助思考的数学意识.特殊化原则是数学学习中的重要思维方式,教师需要基于特殊化原则思维结构的剖析,培养学生的直觉思维、合情推理能力和探索与创新能力.特殊化原则不仅是思考数学问题的重要方法,也是思考一般科学问题的重要方法.
参考文献
[1]中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022:3.
[2][德]克里斯蒂安·黑塞.像数学家一样思考[M].何秉桦,黄建纶,译.海口:海南出版社,2018:127-129.
[3]任璋辉.数学思维论[M].南宁:广西教育出版社,1990:154-155.
[4]张丽玉.初中数学资优生特殊化策略解几何题的实证研究[D].上海:华东师范大学,2020:44.
[5]阴东升,卞瑞玲,徐本顺.数学中的特殊化与一般化[M].南京:江苏教育出版社,1995:94,97.
[6]何华兴.数学中的一般化与特殊化例谈[J].数学通报,2009,48(02):8-10.
[7]朱青锋.特殊化方法的教育学功能[J].数学通报,2002(03):13-14.
作者简介 李亞琼(1983—),女,安徽巢湖人,高级讲师,博士研究生;主要从事数学课程与教学研究.
徐文彬(1966—),男,安徽宣城人,教授,博士生导师;主要从事数学课程与教学研究.
宁连华(1966—),男,江苏丰县人,教授,博士生导师;主要从事数学教育研究.
基金项目 江苏省中小学教学研究课题“教师研究的理论思考与模式建构”(2021JY14_L390);江苏省研究生科研与实践创新计划项目“高中数学整体教学设计的模式建构与实践应用”(SJCX22_0506);安徽省2021年高校协同创新项目“‘双减背景下教学和谐的理论证成、实践省察与行动建构”(GXXT-2021-058).
