基于深度学习的概念课实践

申月

摘 要：借助《函数的零点与方程的解》这一高中数学概念课的教学实践过程，从深度学习的必要性，深度学习的课堂实践以及深度学习的教学启示等方面展开，阐述深度学习下概念课的教学模式，引领并指导数学教学与学习.

关键词：深度学习；函数；零点；方程；概念

深度学习是机器学习的一种，是实现人工智能的必经路径，是一个源于人工神经网络的研究的概念.课堂教学中，借助合理的深度学习，全面构建数学学习共同体，是提升课堂教学效果的一个重要途径.特别在概念教学过程中，深度学习显得更为重要.

1 深度学习的必要性

1.1 探究概念的来龙去脉

借助深度学习，合理挖掘概念的根源，培养学生对知识探究的浓厚兴趣和探究欲望.学生自主对数学概念进行探究，进而理清概念发展的脉络，构建与之相关的概念体系与数学知识体系，对知识的学习与体系的构建很有帮助.

1.2 促进知识的深层理解

借助深度学习，在对概念的浅层次理解的基础上，学生可以通过对概念等知识的批判性的理解与接收，合理内化，将其融入自身已有的知识系统中去，合理实现新知与旧知的链接，从而促进学生对知识的理解与应用，为知识的迁移与学习拓展更加广阔的空间.

1.3 注重知识的交汇融合

借助深度学习，在相关概念初步学习的基础上，进一步加深其与已知知识的联系与关联，构建起不同知识之间的交汇与融合，有助于学生延伸知识的枝蔓，强化新知识的内化及其与原有知识之间的联系，形成一个良好的认知结构.

1.4 养成良好的核心素养

借助深度学习，在概念等相关知识理解与掌握的基础上，融入数据分析、数学抽象、逻辑推理、数学建模、直观想象以及数学运算等核心素养，学生更能批判性地学习新思想和新知识，并将其巧妙融入到已有的认知与知识体系中去，形成对知识的更深层次的理解，提高学生的思维品质和数学学习能力.

2 深度学习的课堂实践

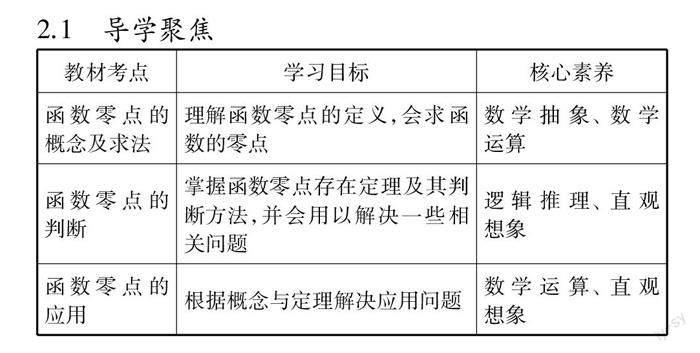
2.1 导学聚焦

理清学习目标与考点，对应相应的核心素养，为概念教学确立了明确的目标与理念，学生围绕这些基本目标来学习.

2.2 问题导学

预习教材（人民教育出版社2019年国家教材委员会专家委员会审核通过的《数学》（必修第一册））第四章《指数函数与对数函数》中4.5函数的应用（二）P142-P144，并思考以下问题：

（1） 函数零点的概念是什么？

（2） 如何判断函数的零点？

（3） 方程的根、函数的图象与x轴的交点、函数的零点三者之间的联系是什么？

强调自主学习，也为深度学习提供条件与过渡.在学生自主学习的基础上，教师通过课堂中的概念教学加以深入，全面提升深度学习的效果.

2.3 概念形成

（1） 概念：对于一般函数f（x），我们把使f（x）=0的实数x叫做函数y=f（x）的零点.

（2） 方程f（x）=0的根、函数f（x）的图象与x轴的交点、函数f（x）的零点三者之间的联系见图1.

问题1：函数的零点是点吗？

提示：函数的零点不是一个点，而是一个实数，当自变量取该值时，其函数值等于零.

问题2：函数的零点个数、函数的图象与x轴的交点个数、方程f（x）=0根的个数有什么关系？

提示：相等.

问题3：结合前面所学的一次函数、二次函数、反比例函数、幂函数、指数函数以及对数函数等相关基本初等函数，思考这些函数是否有零点？并说明理由.

提示：不一定.因为函数的零点其实就是对应方程的根，但不是所有的方程都有根，所以说不是所有的函数都有零点.也可以通过函数的图象与x轴的交点即是对应函数的零点来判断（这里可以结合实例来分析，如反比例函数或指数函数）.

不停留在概念的表层，通过提出问题，反馈信息，深度理解并掌握相关概念的深层次的内涵与实质，也是深度学习的一个层面.

规律方法总结：根据函数的零点（方程的根）情况求解相关参数的取值范围的方法：① 直接法：直接构建相应的不等式，通过含参不等式的求解来确定；② 分離参数法：合理分离参数，利用另一边函数所对应的值域情况来分析与解决；③ 数形结合法：结合函数图象加以直观分析，数形结合处理.

借助零点的应用，多视角多层面地展开，帮助学生有效应用函数的零点概念与函数零点存在定理，也为学生对具体问题的分析与求解提供了条件，进一步总结规律方法，以达到深度学习的目的.

3 深度学习的教学启示

3.1 把握学情，合理设计

数学深度学习具有本源性、联系性、整合性和建构性等基本特征.在实际数学相关概念的教学过程中，教师要充分挖掘数学概念及其对应的课程资源，调动学生的主体性并合理把握学生的实际情况，巧妙设计深度学习的课堂教学实践过程.除此之外，教师还要充分考虑并兼顾概念教学与学生学情两者之间的吻合度，借助合理设计，形成巧妙链接，自然过渡，真正把数学概念落到实处，真正推进数学深度教学，形成学生的有效深度学习.

3.2 缓慢推进，逐步提升

借助数学概念的教学与学习，结合解题研究，从数学概念的浅显理解走向深刻掌握，并借助实例应用，形成学生概念学习的逐渐上升与螺旋前进的过程，是数学教学与解题研究中追求的一种理想状态，需要师生不断交流、反馈与改进，才能帮助学生形成良好的深度学习，培养良好的数学学习习惯，提升数学能力.

借助深度学习，通过数学概念教学，缓慢推进教学流程，逐步完善与概念相关的数学知识体系，有利于帮助学生形成良好的认知结构，逐步实现数学学习从“概念”到“知识”再到“应用”的过渡，做到“学会”到“会学”，并不断过渡到“会用”的数学学习新境界与新阶段，形成数学能力，提升数学品质，发展核心素养.

参考文献：

［1］ 韩文美.高考数学试题的题源探秘［J］.高中生之友，2018（11）：21-22.

［2］ 中华人民共和国教育部.普通高中数学课程标准（2017年版）［S］.北京：人民教育出版社，2018.