评价：学生深度学习的助推器

冯德广

深度学习的展开与推进离不开教师的评价，深度学习需要教师语言评价的撬动与助推。《义务教育数学课程标准（2022年版）》在“评价建议”中指出：“坚持以评促学、以评促教，突出强调教学评价的育人导向作用。”在教学实践中，笔者通过适时的语言评价，让师生有效互动、教与学融为一体，促进了学生的深度学习。

一、引导式评价，引领学生深度体验

评价的出发点和落脚点都应是学生的“学”。课堂教学中的评价，应让学生参与学习活动的体验过程，在体验经历中获得新的感悟和提升，引导学生从学会到会学，从而愿学、乐学。坚持将学生的“学”放在首位，学中有评，以评促学，这样才能使学习活动走进学生心里，让教師的“评”与学生的“学”灵犀相通，提升学生数学素养。

在教学苏教版小学数学教材五年级上册“解决问题的策略（一一列举）”时，教师出示了这样一个数学问题：小红和小力各有8、2、5三张数字卡片，每人拿一张，一共有多少种不同的拿法？学生依次演示了以下三种方法。

第一种：88、82、85、28、22、25、58、52、55；

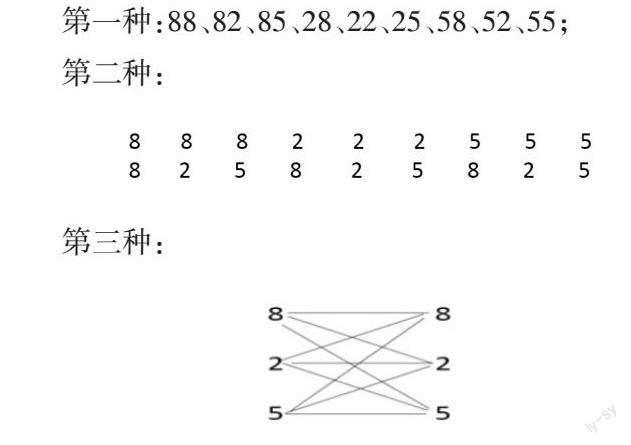
第二种：

第三种：

这个数学问题，不仅考查学生灵活运用其他策略与一一列举有机结合的能力，还隐藏着先分类再列举的教学目标。虽然学生运用三种不同的形式进行列举，但只达成课堂教学掌握知识技能、解决问题的浅层目标，隐藏其中的数学精髓学生并没有领悟，需要教师的引导和点拨。经验丰富的教师不会“就此罢手”，也不会独自表演，而是顺势引导学生继续观察、比较、探究，有效地达成课堂教学中领悟分类思想、积累活动经验的深层目标。教师通过引导式语言进行评价：“这三种方法都能有效、有序地解决问题，说明大家能灵活运用一一列举的策略。它们的策略相同，只是表现形式不同。你们可以仔细体验这三种方法完整的思维过程吗？找一找，比一比，看看它们之间有怎样相同的思维过程？”通过学生综合比较、深度体验、相互交流，有学生发现：小红和小力既可以拿相同的卡片，也可以拿不同的卡片，即分为相同数字和不同数字两类（如图1）。也有学生发现：每一张数字卡片，都对应着三张不同的数字卡片，即小红拿的卡片可以分为三类：8、2、5，每一类中小力也可以拿三种不同的数字卡片8、2、5。还有学生发现：这个数学问题可以通过简单算式来表达，即3×3=9（种）。在教学过程中，教师善于观察学情，充分挖掘课堂生成的学习信息，顺应学生的学习心理，在学生的最近发展区通过适当的评价语言进行顺势引导，引领学生往学习的更深处体验，从而获得对数学知识的理性感悟，促进学生数学素养的提升。

二、质疑式评价，引领学生深度探究

课堂教学中的评价，应该与教学过程融合在一起，成为课堂教学中不可或缺的一部分。在学生探究交流过程中，教师引导学生自评、互评，通过适当质疑，引领学生乐于学习，善于反思，推动课堂探究活动走向深入。

教学苏教版小学数学教材六年级下册“圆柱与圆锥的认识”时，学生认识完圆柱之后，教师接着出示圆锥学具，提出这样一个数学问题：“你认为这个圆锥的侧面展开后，会是什么图形？”学生刚刚经历圆柱侧面展开的过程，以及初步认识圆锥的立体特征，纷纷在头脑中联想出圆锥侧面展开后可能的形状：有的学生认为是圆形，有的学生认为是扇形，还有的学生认为是三角形。教师并没有给学生的个性思考进行任何点评，而是集中一起一边评价一边质疑道：“同学们，圆锥侧面由立体转化成平面，大家根据圆锥的初步认识，主动进行联想，形成了三种观点，非常厉害！有的观点只关注圆锥部分特征，而忽视了圆锥其他部分特征，你们认为应该排除哪一种观点？为什么？”

学生认为：“圆锥的侧面展开不可能是三角形，因为三角形的边是线段，是直的，而圆锥底面是圆，应该是弧，是弯曲的。”全班学生纷纷点头称是。但是另外两种观点，学生各执一词，莫衷一是。有的学生认为，展开后圆锥的顶点应该是圆的圆心，圆锥的侧面应该是一个圆；也有的学生认为，展开后圆锥的侧面不够拼成一个圆，只是圆的一部分，是一个扇形，圆锥的顶点应该是扇形的圆心。教师继续问道：“你们继续深挖圆锥的特征，展开丰富的想象，都具有一定的合理性。那么，圆锥的侧面展开后究竟是圆形还是扇形呢？”这时，操作实验成为验证这两种观点的迫切需求。教师拿出事先准备好的教具：一个扇形和一个圆形纸片，指名两个学生上台分别围一围。在两个学生动手操作中，课堂纷争自然而然地解决了。

当学生出现片面的错误时，教师通过第一次质疑式评价，引导学生聚焦圆锥底面特征进行想象，推进学生探究的历程。学生根据圆锥的特征无法辨别另外两种观点哪一种正确，此时，学生出现混乱的想象，集体不知所措。教师通过第二次质疑评价，操作实验跃上课堂教学的舞台，成为验证学生想象的法宝，充分调动学生的内驱力，激发了学生往知识更深处探究的欲望。

三、追问式评价，引领学生深度建构

著名教育心理学家布鲁姆认为：评价是一种获取和处理用以确定学生水平和教学有效性的证据的方法。课堂教学中的评价，应该以学生的学习心理为依据，符合学生的学习需求与课堂节奏，能激发学生主动参与深层次的数学活动的意愿，促进学生产生强烈的学习心向，参与数学知识意义建构，提升学生数学素养。

在教学苏教版小学数学教材五年级下册“分数的初步认识”时，教师设计了这样一个数学活动：每人拿出一张纸，先折一折，再把它的[12]涂上颜色。学生完成后，教师让他们把作品依次贴在黑板上，相同的就不要贴。接着，教师引导学生欣赏黑板上各式各样的学生作品，说道：“你们的小手真灵巧！竟然折出这么多丰富多彩的作品，其中哪一幅作品与众不同？”学生用审视的目光一一辨别，同中找异——把没有平均分的作品撤掉。然后，教师又追问：“剩下这些作品都共同关注了数学问题的重点！你们认为重点在哪里？”学生把目光又一次聚焦到这些作品上，异中找同——把大小不一、形状各异、颜色不同的纸平均分成两份。此时，教师继续追问：“同一幅作品中，两个部分完全相同。但是，不同的作品中，涂色部分的形状不一样，为什么都可以用[12]表示？”引导学生继续深度思考，剔除大小、形状、色彩等非本质属性，探究出只要把一张纸平均分成两份，其中一份就是这张纸的[12]的本质属性。这样，学生的思维逐渐排除非本质属性的干扰，从中发现隐藏的相同规律，感悟[12]的本质内涵。层层深入、追根刨底式的追问，不仅从正面评价学生探究的成果，还引发学生关注探究过程，即使有些学生折纸时只是浅层次的动手操作，他们也会在教师的追问下，知其然也知其所以然，从而深度建构数学概念。

（作者单位：江苏省扬州市育才小学东区校）