打破认知壁垒，建构分数意义

金妤茜

数的认识贯穿于整个小学阶段，不同的数看似不同，背后却有着密切联系。“认识几分之一”是苏教版小学数学教材三年级上册“分数的初步认识”单元的教学内容，不仅是整个单元的起始课，还是小学阶段学习分数的起始课。通过本课学习，学生认识的数由整数扩展到了有理数，这是学生认数过程中的一次质的飞跃。分数和整数一样，具有可数性、可比性，这一内容的学习也为学生后续进一步认识分数和小数打下重要的基础。

分数的概念看似简单，却较为抽象，对于三年级的学生来说有一定的认知难度。在教学中，我们该如何突破简单的“认识”，有效地、高质量地建构分数概念呢？笔者有幸聆听了特级教师李保伟老师“认识几分之一”一课，课堂上，李老师巧妙设计，通过多次打破学生认知，引导学生在深度思考中经历和体验认识分数的过程，掌握分数的概念，发展数学思维。下面，笔者对这节课中的一些教学片段进行简要的呈现与赏析，与大家共赏。

【片段一】第一次打破认知，引出分数：在数的分与合中初识[12]

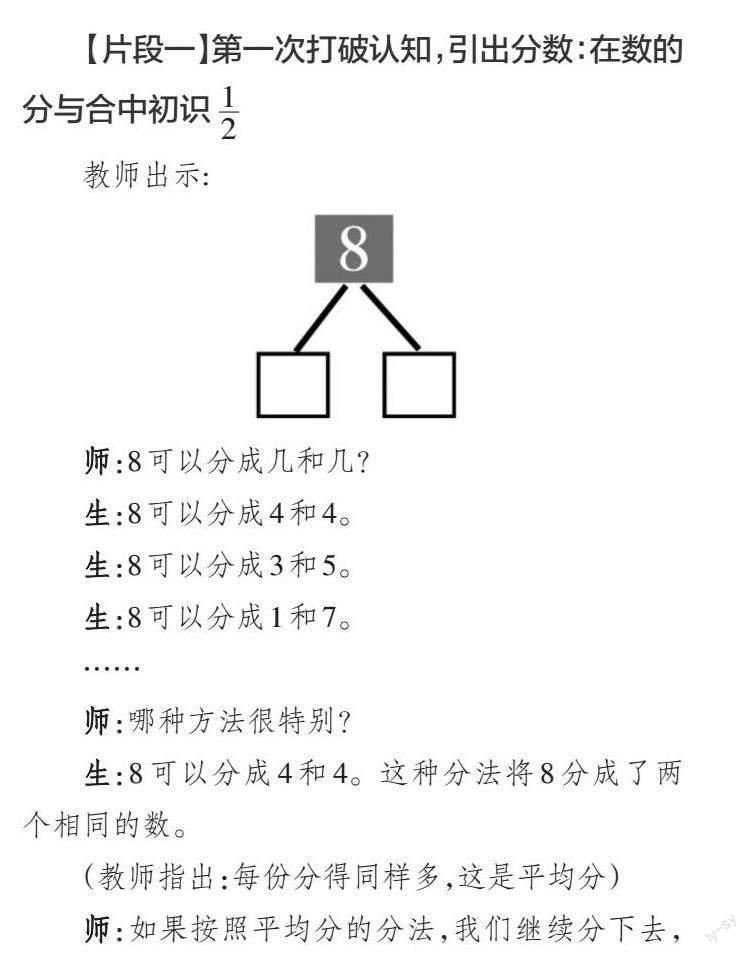
教师出示：

师：8可以分成几和几？

生：8可以分成4和4。

生：8可以分成3和5。

生：8可以分成1和7。

……

师：哪种方法很特别？

生：8可以分成4和4。这种分法将8分成了两个相同的数。

（教师指出：每份分得同样多，这是平均分）

师：如果按照平均分的分法，我们继续分下去，会怎么样？

学生口答，教师利用课件依次呈现：

师：1继续往下平均分，会是多少呢？

生：0.5和0.5。

生：[12]和[12]。

师：这两种答案，谁听懂了？与前面的平均分一样吗？

生：不一样，前面的平均分最后都是分成两个整数。

生：1继续平均分就不是整数了。

【赏析】数学知识是相互联系、不断生长的，数学的整体性特征决定了每节课中新知识的学习都是旧知识的延伸与发展。认知的本质是适应，儿童的数学认知是在原有知识的基础上，通过对思维的刺激，将新知识纳入已有的知识结构中，使认知不断地从低级向高级发展。教学中，李保伟老师巧妙地从数的分与合出发，有效唤醒学生原有的“平均分”的经验，为由整数向分数的过渡做好铺垫。紧接着再将1继续往下平均分时，学生在表达平均分的结果时产生相应的认知冲突，吸引学生自觉进行数概念的扩展，使新数的认识水到渠成，分数的概念呼之欲出。

【片段二】第二次打破认知，深化意义：在对比变式中理解[14]

1.类比与思考：在图1至图4中，折法不同，涂法不同，为什么涂色部分都能表示这张纸的[14]？

师（小结）：只要把正方形纸平均分成4份，取其中的1份，就表示这张纸的[14]。

2.借助“[14]”，理解分数的组成部分和相关含义。

师：通过刚才的活动，[14]该怎么写呢？先写横线，再写4，最后写1。这条横线在分数里面有一个特定的名字，叫作分数线，代表平均分。

师：这个4是分母，表示什么？

生：表示平均分成了4份，分母代表平均分的总份数。

生：1是分子，代表的是取其中的1份。

师：这也就是为什么同样一个正方形它的折法不一样，但折出来的涂色部分都能表示[14]。

3.下面这3个涂色部分还能表示整个图形的[14]吗？为什么？

教师出示图5至图7。

生：图5不能，因为没有平均分。

生：图6和图7可以，我们可以旋转和平移一下就知道了。

师（小结）：有时候平均分不是一眼就能看出来，需要运用旋转或平移等知识去判断。但只要是平均分成了4份，取了其中1份，就可以用[14]来表示。

【赏析】概念是事物本质特征的反映，教师要引导学生精准把握事物的本质特征，从而形成概念。在学生初步感悟分数的意义后，李保伟老师引导学生重点认识[14]，抓住关键问题巧妙追问：折法不同，涂法不同，为什么涂色部分都能表示這张纸的[14]？学生在思考这一问题时将眼光聚焦到分数的本质特征上，在分析说理后顺势介绍[14]的组成部分和相关含义，将抽象概念与图形表征对应起来，加深对分数知识的理解。紧接着李老师更是以一道变式题，鼓励学生进行判断，从“完整的涂色部分”到“不完整的涂色部分”，再次打破了学生的认知，学生要用心观察、对比分析，尝试把图形平均分和运用平移、旋转的方法把两块图形拼成一块后进行判断，学生从迷茫到笃定，这一过程不仅帮助学生进一步认识了分数，更让学生的思维得到了发展。

【片段三】第三次打破认知，贯通计数单位：在整体联系中再识分数

师：请看这个分数墙（图8），看第一行，我们把1分成了几个几呢？

师：同学们，像这种几分之一，它既是分数单位，也是我们以前熟悉的计数单位。以前我们知道，整数的计数单位进率是10，那分数的计数单位要怎么看？

生：看分母。

师：分母有可能是2，也有可能是3。有可能是10，也有可能是100，还有可能是1000。如果是10、100、1000……的时候分数就可以摇身一变，变成一开始你们说的小数。

【赏析】《义务教育数学课程标准（2022 年版）》指出：“课程内容的设计要体现整体性、一致性。教学时，教师需要整体把握知识的内在结构与发展路径，进行知识之间的整体关联。”本节课在学生基本认识和理解了几分之一后，李老师通过复习回顾旧知识，借助“分数墙”引导学生在对比学习中发现：分数的分数单位与自然数的“个、十、百、千”一样都是计数单位，只不过不同的分母，对应不同的计数单位。这一过程将分数知识置于整体的知识体系中，引导学生感受知识的整体性，体现出计数单位和分数单位的对应性与一致性，使本节课的教学价值得到更好的发挥。

整节课，李老师从知识的整体性、策略的一致性等方面注重把学生已有的数数经验和认知结构打通，使学生主动地投入分数的学习中去，引导学生学会从知识整体视角看整个分数体系，提升学生的数学思维能力，启迪学生的智慧。

（作者单位：江苏省苏州工业园区星港学校）